Преобразование Лапласа. Передаточные функции одномерной ЛСС и её элементов (тема 2.2)

1.

Автоматика и управление
Тема 2. Передаточные функции и
структурные преобразования ЛСС
Лекция 2. Преобразование Лапласа. Передаточные
функции одномерной ЛСС и её элементов. Структурная
схема АС. Передаточные функции соединений звеньев.
Элементы автоматики – функционально полный набор
элементарных динамических звеньев САУ и САР, их
математический аппарат.

2.

2.1 Преобразование Лапласа
Преобразование
Лапласа
интегральное
преобразование,
связывающее
функцию
F(p)
комплексного переменного (изображение) с функцией
f(x) действительного переменного (оригинал).
Преобразованием Лапласа от функции f(x) (оригинала)
называется функция:
f(x) называют оригиналом преобразования Лапласа, а
F(p) - изображением преобразования Лапласа. f(x) и
F(p) однозначно определяются друг относительно друга,
то есть если Вы знаете f(x), то всегда можете узнать
F(p), и наоборот, если знаете F(p), то всегда можете
получить f(x).

3.

Прямое одностороннее преобразование Фурье
определяется формулой
x( j ) x (t )e _ j t dt
0
Преобразование Фурье может быть
применено к функции x (t), для которых
интеграл
| x(t ) | dt
0
существует (условие абсолютной интегрируемости). Этому условию не
удовлетворяют многие функции, используемые при исследовании систем:
t
l(t), Аsin(t), е ,Аcos(t), некоторые решения дифференциальных уравнений.
чтобы иметь возможность подобную функцию x(t) преобразовать по Фурье,
предварительно ее надо умножить на функцию e t
где вещественное число 0 выбрано таким образом, чтобы интеграл
t
|
x
(
t
)
|
e
dt был сходящимся.
0
В результате запишем
x( j , ) x(t )e t e j t dt x( j )
0
Введем новую комплексную переменную p= j
X ( p ) x(t )e pt dt
0

4.

Преобразование Лапласа
Обратное преобразование Лапласа
j
1
1
pt
Y
(
p
)
e
dp
F ( p ) L [ f ( t )] f ( t )e pt dt y (t ) L [Y ( p )]
2 j j
0
Свойства преобразования Лапласа
1. Изображение производной
L(x(n)(t))=pnX(p) - pn-1x0 - pn-2 x0( 1 ) px0( n 2 ) x0( n 1 )
x0 , x0(1) , , x0( n 1) - ненулевые начальные условия функции x(t)
При нулевых Н.У.
x0 , x0(1) , , x0( n 1) 0
L[x(n)(t)]=pn X(p)
2. Изображение интеграла
L[ x(t )dt ] X ( p) / p
0
3. Теорема о сдвиге
L[ x(t )] X ( p)e p
4. Линейность преобразования L[x(t)+y(t)] = L[x(t)]+L[y(t)], а
следовательно L[x(t) y(t)] ≠ L[x(t)] L[y(t)]

5.

2.2. Передаточные функции одномерной ЛСС и её
элементов
Для одномерной ЛСС с одним входом передаточной функцией
Ф(р) называется отношение изображения по Лапласу
выходного сигнала к изображению по Лапласу входного
сигнала при нулевых начальных условиях:
Y( p )
Ф(р)=
,
X( p )
X ( p) L[ x(t )] x(t )e pt dt
изображение входного сигнала
Y ( p) L[ y(t )] y(t )e pt dt
изображение выходного сигнала
0
0
p= +j - комплексная переменная
x(t)
A[x(t)]
y(t)
X(p)
Ф(р)
Y(p)

6.

Если задан входной сигнал x(t) и известна передаточная
функция системы Ф(р), то однозначно определяется выходной
сигнал АС.
1) по заданному x(t) определить X(p)=L[x(t)] (как правило, с
помощью таблиц);
2) определить Y(p) по равенству Y(p)=X(p)Ф(р);
3) по изображению выходного сигнала Y(p) определить его
оригинал, используя формулу обратного преобразования
Лапласа (как правило, с помощью таблиц или по теореме
разложения ).
Передаточная функция Ф(р) - это динамическая
характеристика системы, позволяющая определить связь
между входным и выходным сигналами, т.е. оператор АС.
Как определить Ф(р), если входной сигнал x(t) и выходной - y(t)
неизвестны, а известен оператор АС ?

7.

Передаточные функции ЛСС бывают двух типов:
- передаточная функция ЛСС с оператором, задаваемым
л.д.у. при нулевых начальных условиях;
- передаточная функция ЛСС с оператором постоянного
запаздывания.
Для одномерной ЛСС с одним входом, задаваемой
оператором в виде л.д.у.
any(n)(t)+ + a1y(1)(t)+ a0y(t)= вmx(m)(t)+ + в1x(1)(t)+ в0x(t)
(1)
с нулевыми начальными условиями и m n, передаточная
функция Ф(р) является рациональной функцией комплексной
переменной р с вещественными коэффициентами:
m
Ф(р)
вm p m в1 p в0
аn p a1 p a0
n
вi p i
i n0
ai p i
i 0
B( p )
A( p )
(2)

8.

Из выражения (2) следует:
1. Ф(р) - не зависит от вида входного сигнала x(t), а зависит
от параметров АС.
2. Ф(р) - однозначно определяется оператором АС.
Правило:
Если оператор АС задан в виде (1), то для определения Ф(р)
необходимо:
а) в числителе записать правую часть оператора, заменяя
x(i)(t) на pi,
б) в знаменателе записать левую часть оператора, заменяя
y(i)(t) на pi.
Примеры:
Ф(р)
3y(3)(t) - 2y(1)(t)+5y(t)=10x(2)(t)
в1 р в0
а2 р а1 р а0
2
Ф(р)
10р 2
3 р3 2 р 5
a2 y(2)(t)+a1 y(1)(t)+a0 y(t)=в1 x(1)(t)+в0x(t)

9.

3. Числитель передаточной функции –B(p) является
полиномом порядка m комплексной переменной p с
действительными коэффициентами вi .
Корни qi полинома В(р) называются нулями передаточной
функции, т.к. они удовлетворяют равенствам:
В(qi)=0,
i=1,2,…,m;
Ф(qi)=0.
4. Знаменатель передаточной функции - А(р) называется
характеристическим полиномом АС и является полиномом
порядка n комплексной переменной p с действительными
коэффициентами ai.
Корни характеристического полинома рi называются
полюсами передаточной функции, т.к. они удовлетворяют
равенствам:
A(pi)=0,
i=1,2,…,n;
Ф(pi)= .

10.

Нули qi и полюса pi передаточной функции, как корни
полиномов с действительными коэффициентами, могут быть
либо вещественными, либо комплексно-сопряженными.
jI
q2
p2
R
q1
p1
p3
p4
-полюс,
○ -нуль,
р1=-а, р4=в,
р2,3=-с j 1
q1=l,
q2,3= j
q3
Комплексно-сопряженные нули и полюса располагаются на
комплексной плоскости симметрично относительно
вещественной оси.
4. Для технически реализуемых систем Ф(р) - правильная
рациональная дробь, так как m n.

11.

3.2. Передаточная функция звена постоянного
запаздывания
Для одномерной ЛСС с одним входом, задаваемой
оператором постоянного запаздывания
y(t)=K x(t- )
(4)
передаточная функция имеет вид:
Ф(р)=Ке-р
L[y(t)]=Y(p), L[K x(t- )]=KX(p)е-р
Y(p)= KX(p)е-р
Ф(р)
Y(p)
К е-р
X(p)

12.

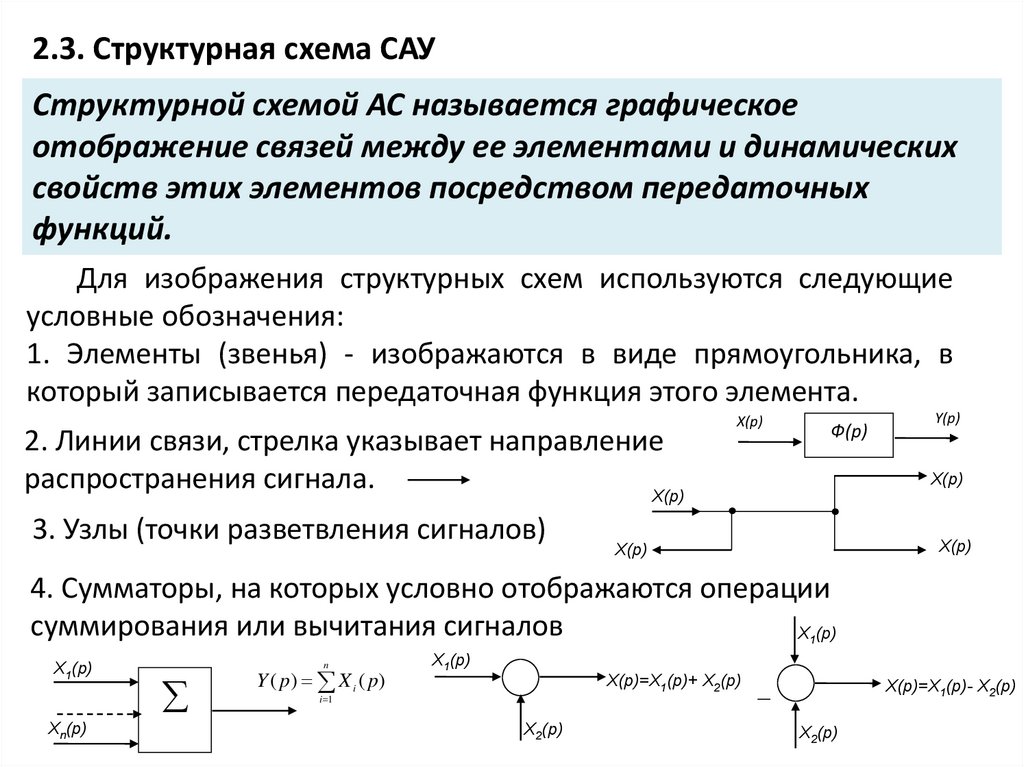
2.3. Структурная схема САУ
Структурной схемой АС называется графическое
отображение связей между ее элементами и динамических
свойств этих элементов посредством передаточных
функций.
Для изображения структурных схем используются следующие
условные обозначения:
1. Элементы (звенья) - изображаются в виде прямоугольника, в
который записывается передаточная функция этого элемента.
2. Линии связи, стрелка указывает направление
распространения сигнала.
X(p)
3. Узлы (точки разветвления сигналов)
X(p)
Ф(р)
Y(p)
X(p)
X(p)
X(p)
4. Сумматоры, на которых условно отображаются операции
суммирования или вычитания сигналов
X (p)
1
X1(p)
Xn(p)
n
Y ( p) X i ( p)
X1(p)
X(p)=X1(p)+ X2(p)
i 1
X2(p)
X(p)=X1(p)- X2(p)
X2(p)

13.

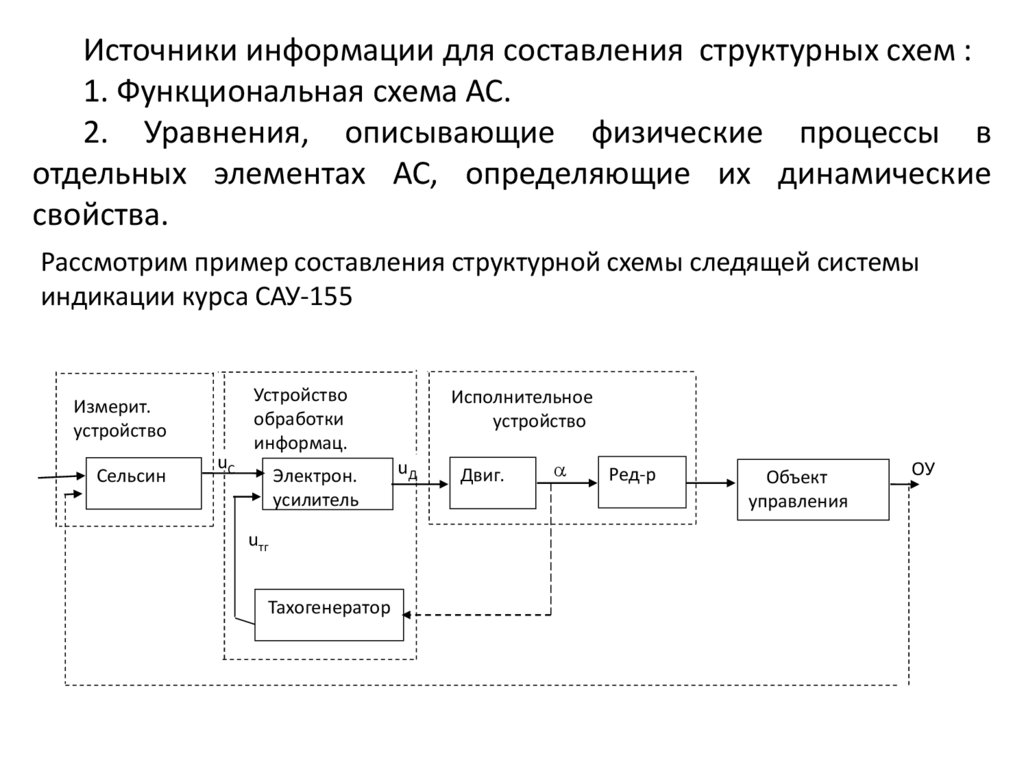
Источники информации для составления структурных схем :
1. Функциональная схема АС.
2. Уравнения, описывающие физические процессы в
отдельных элементах АС, определяющие их динамические
свойства.
Рассмотрим пример составления структурной схемы следящей системы
индикации курса САУ-155
Измерит.
устройство
Cельсин
uС
Устройство
обработки
информац.
Электрон.
усилитель
uтг
Тахогенератор
Исполнительное
устройство
uД
Двиг.
Ред-р
Объект
управления
ОУ

14.

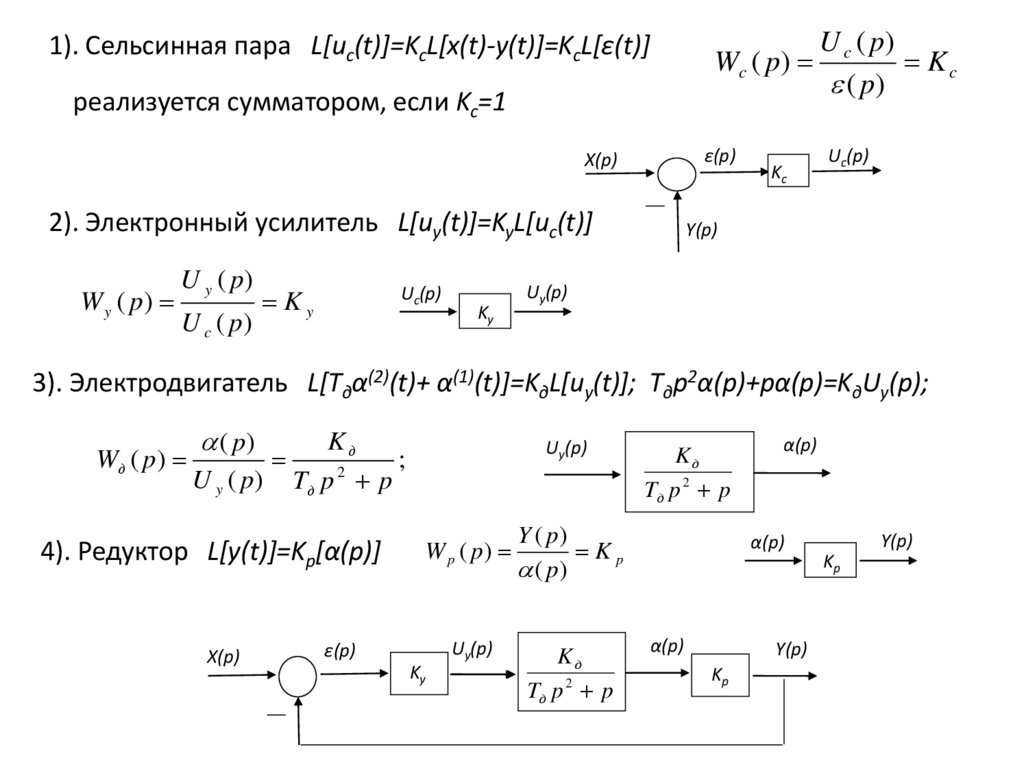
1). Сельсинная пара L[uc(t)]=KcL[x(t)-y(t)]=KcL[ε(t)]
Wc ( p)
U c ( p)
Kc
( p)
ε(p)
Uc(p)
реализуется сумматором, если Kc=1
X(p)
2). Электронный усилитель L[uy(t)]=KyL[uc(t)]
W y ( p)
U y ( p)
U c ( p)
Ky
Uc(p)
Ky
Kc
Y(p)
Uy(p)
3). Электродвигатель L[Tдα(2)(t)+ α(1)(t)]=KдL[uy(t)]; Tдp2α(p)+pα(p)=KдUy(p);
Wд ( p )
( p)
U y ( p)
Kд
Tд p 2 p
4). Редуктор L[y(t)]=Kp[α(p)]
X(p)
Uy(p)
;
W p ( p)
Y ( p)
Kp
( p)
Uy(p)
Kд
Tд p 2 p
ε(p)
Ky
Kд
Tд p 2 p
α(p)
α(p)
α(p)
Y(p)
Kp
Y(p)
Kp

15.

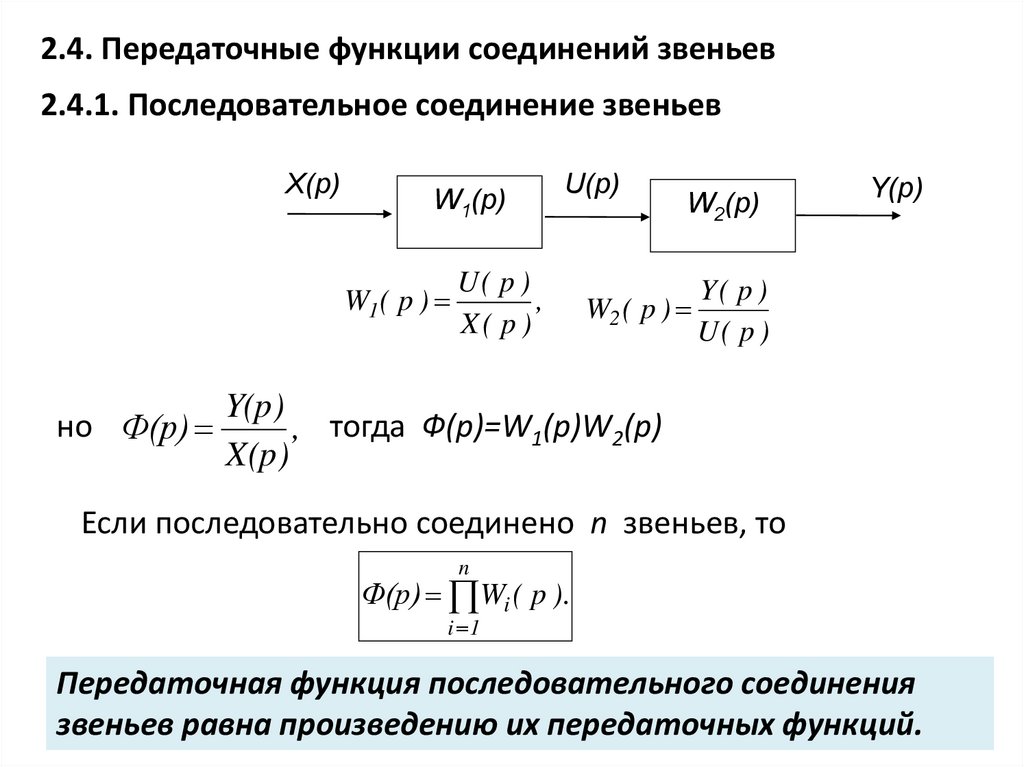
2.4. Передаточные функции соединений звеньев
2.4.1. Последовательное соединение звеньев
X(p)
W1(р)
W1 ( p )
но Ф(р)
U(p)
U( p )
,
X( p )
W2(р)
W2 ( p )
Y(p)
Y( p )
U( p )
Y(p)
, тогда Ф(р)=W1(p)W2(p)
X(p)
Если последовательно соединено n звеньев, то
n
Ф(р) Wi ( p ).
i 1
Передаточная функция последовательного соединения
звеньев равна произведению их передаточных функций.

16.

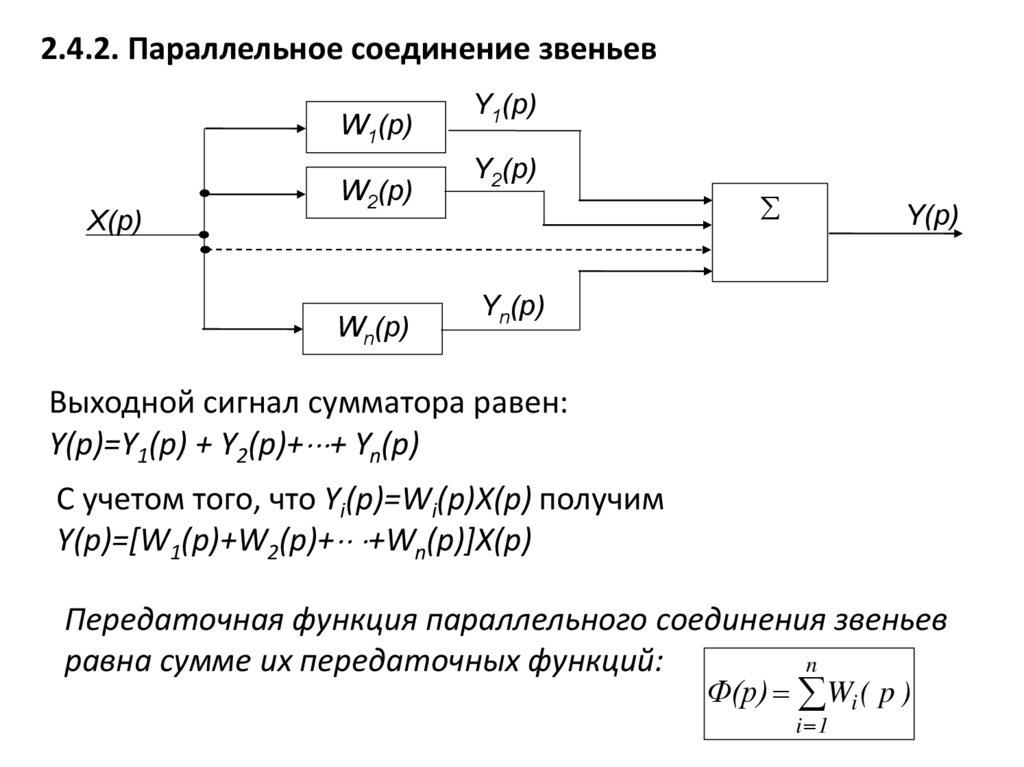
2.4.2. Параллельное соединение звеньев
W1(р)
X(p)
W2(р)
Wn(р)
Y1(p)
Y2(p)
Y(p)
Yn(p)
Выходной сигнал сумматора равен:
Y(p)=Y1(p) + Y2(p)+ + Yn(p)
С учетом того, что Yi(p)=Wi(p)X(p) получим
Y(p)=[W1(p)+W2(p)+ +Wn(p)]X(p)
Передаточная функция параллельного соединения звеньев
равна сумме их передаточных функций:
n
Ф(р) Wi ( p )
i 1

17.

2.4.3. Встречно - параллельное соединение звеньев
(p)
X(p)
W1(р)
U(p)
где
W2(р)
соединение с отрицательной обратной
связью
соединение с положительной обратной
связью
(p)=X(p)( )U(p), (1)
Y(p)= (p)W1(p), (2)
U(p)=Y(p)W2(p)
(3)
Y(p)
(р)=X(p)-U(p) изображение сигнала
рассогласования
Подставим уравнение (1) в выражение (2):
Y(p)=[X(p)( )U(p)]W1(p)
(4)
Подставим равенство (3) в формулу (4):
Y(p)( )Y(p)W2(p)W1(p)=W1(p)X(p)
Ф(р)
Y(p)
W1 ( p)
X(p) 1( )W2 ( p)W1 ( p)

18.

Передаточная функция встречно - параллельного
соединения звеньев равна отношению передаточной
функции звена расположенного в прямом тракте
соединения к сумме (разности) единицы и передаточной
функции разомкнутого соединения:
W(p)= W1(p) W2(p).
Знак “+”относится к системам с отрицательной обратной связью,
а знак “-” к системам с положительной обратной связью.
Частным случаем встречно - параллельного соединения
является соединение с единичной обратной связью, т.е.
W2(p)=1.
Y(p)
(p)
X(p)
W1(р)
Такое встречно - параллельное соединение называют
соединением с жесткой обратной связью и его Ф(р) имеет
W1 ( p)
вид:
Ф(р)
1( )W1 ( p)

19.

2.5. Эквивалентные структурные преобразования ЛСС
При исследовании АС широко используют структурные
преобразования.
Цель структурных преобразований - упростить исходную
структурную схему к более простой, эквивалентной и
удобной для анализа структурной схеме.
Две структурные схемы называются эквивалентными, если
они определяют одинаковую взаимосвязь между заданным
входом и соответствующим выходом, то есть, если им
соответствуют одинаковые передаточные функции.
Основное
правило
эквивалентных
структурных
преобразований: эквивалентные структурные схемы АС или
ее части определяют одинаковую взаимосвязь между
заданными входными и соответствующими выходными
сигналами.

20.

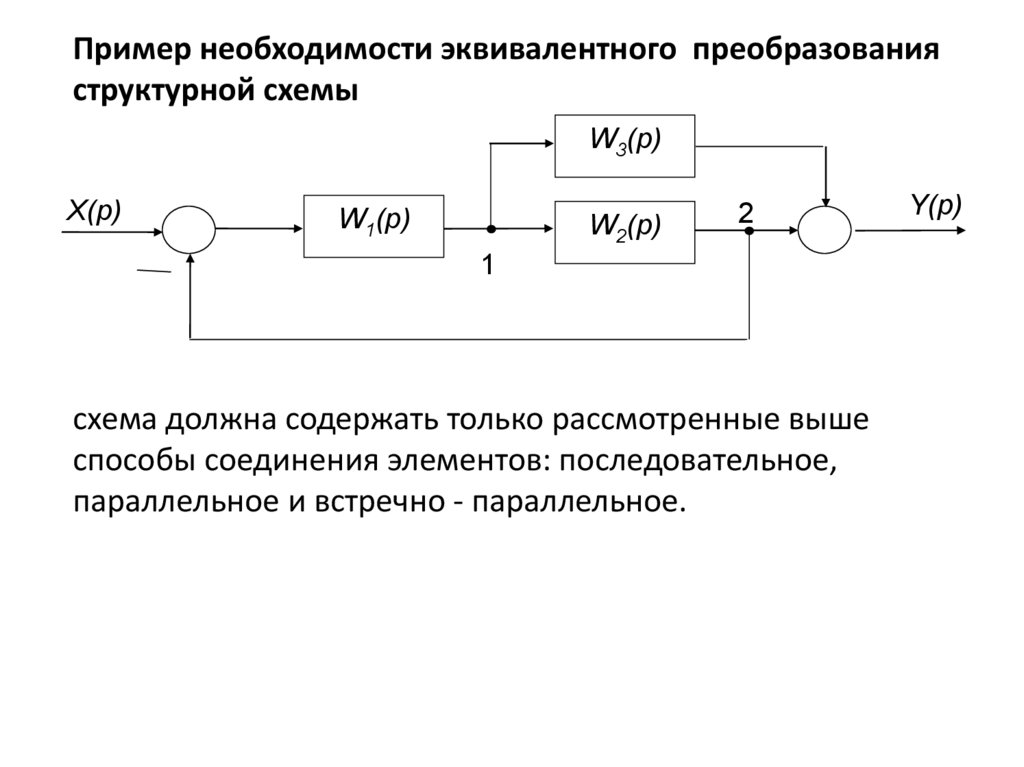
Пример необходимости эквивалентного преобразования
структурной схемы
W3(р)
X(p)
W1(р)
W2(р)
2
1
схема должна содержать только рассмотренные выше
способы соединения элементов: последовательное,
параллельное и встречно - параллельное.
Y(p)

21.

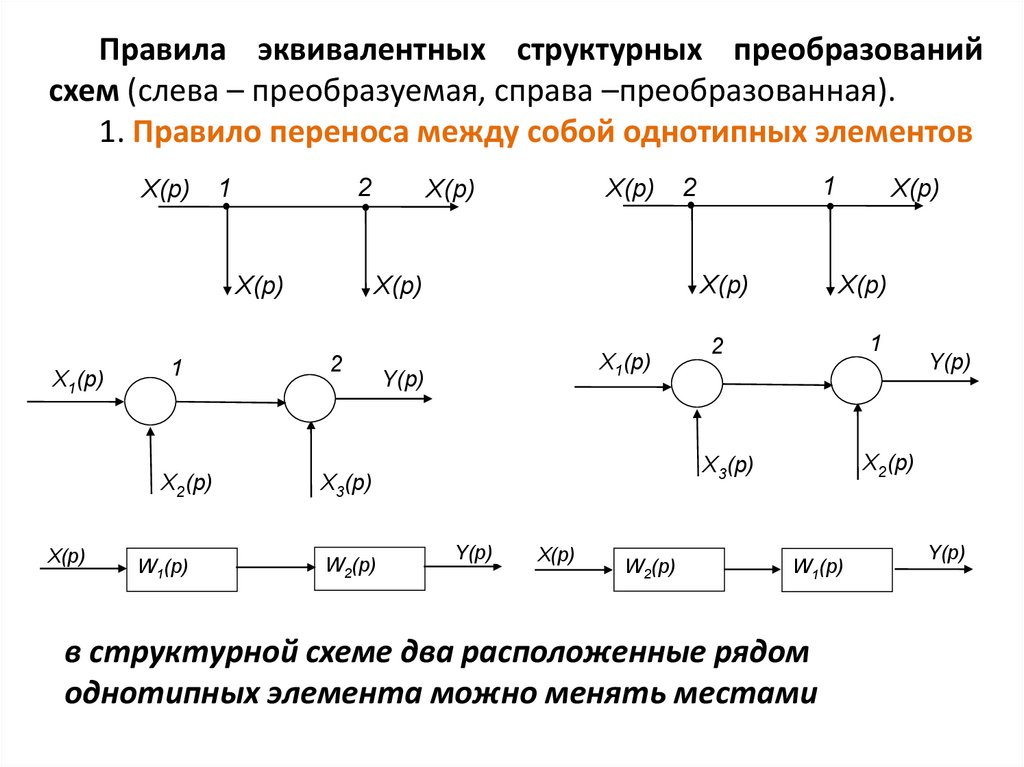
Правила эквивалентных структурных преобразований
схем (слева – преобразуемая, справа –преобразованная).
1. Правило переноса между собой однотипных элементов
X(p)
2
1
X(p)
X1(p)
1
X2(p)
X(p)
W1(p)
X(p)
X(p)
X(p)
2
X1(p)
Y(p)
X3(p)
W2(p)
Y(p)
X(p)
W2(p)
1
2
X(p)
X(p)
X(p)
2
1
X3(p)
X2(p)
W1(p)
в структурной схеме два расположенные рядом
однотипных элемента можно менять местами
Y(p)
Y(p)

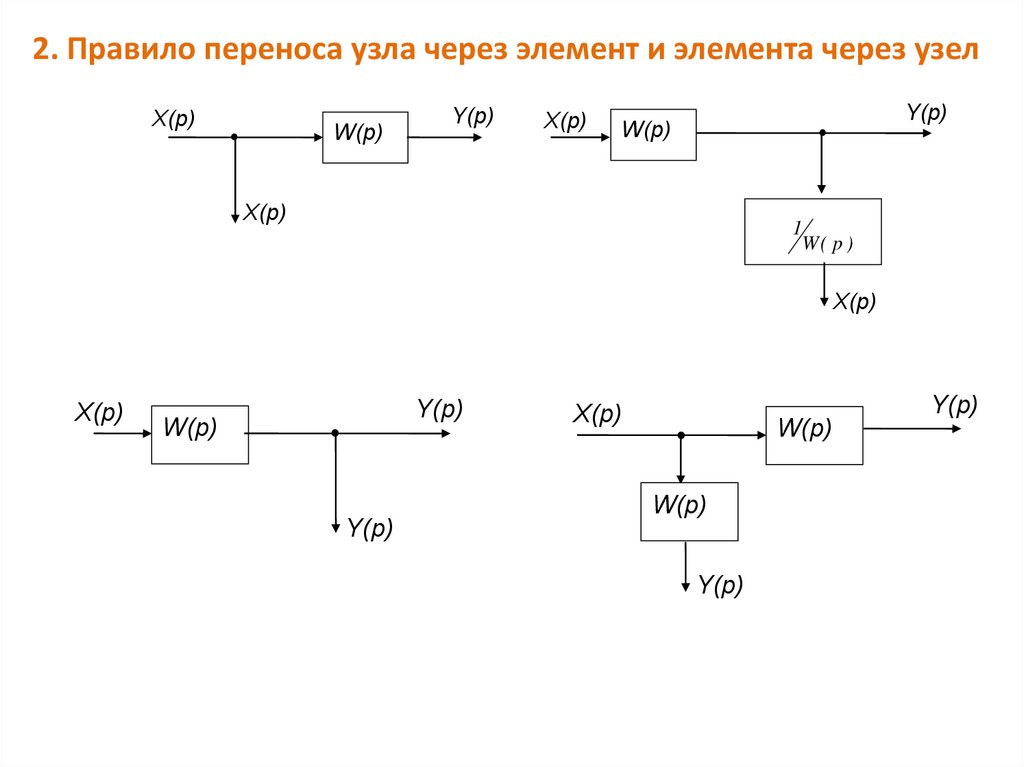
22.

2. Правило переноса узла через элемент и элемента через узел
X(p)
W(p)
Y(p)
X(p)
Y(p)
W(p)
X(p)
1
W( p )
X(p)
X(p)
Y(p)
W(p)
Y(p)
X(p)
W(p)
W(p)
Y(p)
Y(p)

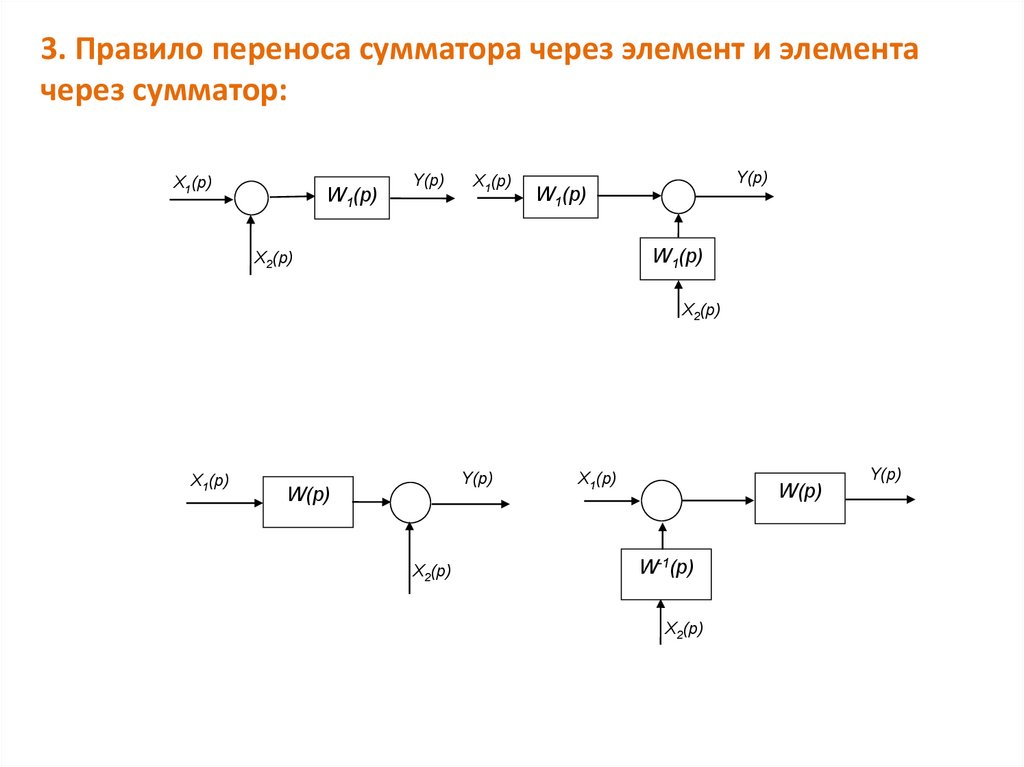
23.

3. Правило переноса сумматора через элемент и элемента
через сумматор:
X1(p)
W1(р)
Y(p)
X1(p)
Y(p)
W1(р)
W1(р)
X2(p)
X2(p)
X1(p)
Y(p)
W(р)
X2(p)
X1(p)
W(р)
W-1(р)
X2(p)
Y(p)

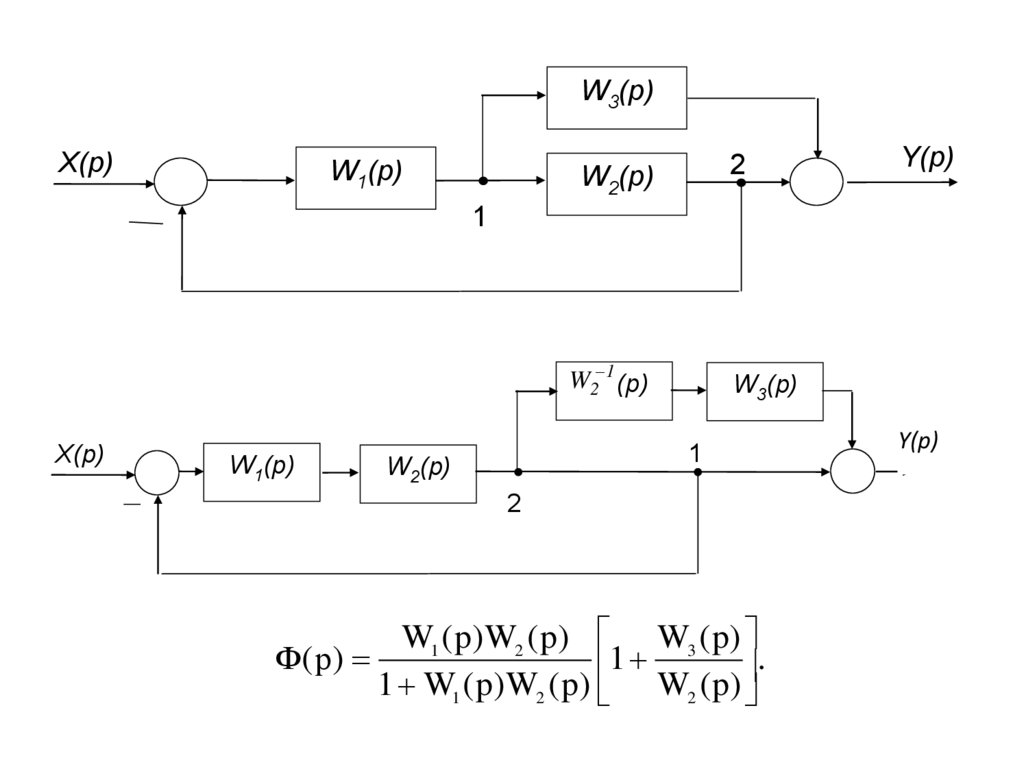
24.

W3(р)
X(p)
W1(р)
W2(р)
2
W2 1 (р)
W3(р)
Y(p)
1
X(p)
W1(р)
1
W2(р)
2
W1 ( p) W2 ( p) W3 ( p)
Ф( р )
1
.
1 W1 ( p) W2 ( p) W2 ( p)
Y(p)

25.

2.6. Элементы автоматики – функционально полный набор
элементарных динамических звеньев САУ и САР, их
математический аппарат
Элементарными динамическими звеньями называют
простейшие элементы АС, описываемые передаточными
функциями рационального вида
m
i
в
p
i
W ( p ) i n0
i
a
p
i
,
m=0,1,2…; n=0,1,2...
(5)
i 0
с вещественными коэффициентами аi и вi которые не
могут быть представлены произведением более простых
передаточных функций.

26.

На основании теоремы Безу, запишем передаточную функцию
ЛСС Ф(р), используя ее нули qi и полюса pi:
вm p m вm 1 p m 1 в0 вm ( p q1 ) ( p qm )
Ф( p )
n
n 1
an p an 1 p a0 an ( p p1 ) ( p pn )
(6)
можно выделить три вида сомножителей
вm
K
an
(7)
1
Wi ( p )
p pi
рi=0 тогда
Wi ( p )
~
Wi ( p) p qi
1
1
p 0 p
(8)
pi=- i где i - вещественное положительное число
Wi ( p)
Ki
1
p i Ti p 1
Ki
1
Ti
1
. (9)
i
i
рi=- i+j i, где i>0, i>0 - вещественные числа,
не отвечает виду (5)
рi+1=- i-j i
Wi ( p )
1
p i j i
Wi 1 ( p )
1
p i j i
.

27.

Произведение выражений Wi(p) и Wi+1(p) ?
Wi ( p)Wi 1 ( p ) Wi ( p )
1
( p i j i )( p i j i )
Ki
1
1
,
2
2
2
2
2
2 2
( p i ) i
p 2 i p ( i i ) Ti p 2 i Ti p 1
Ki
1
;
2
i2 i
Ti
1
;
2
i2 i
i
ai
i2 i2
.
(10)

28.

~
Wi ( p)
qi=0, тогда
в m p m в m 1 p m 1 в 0 в m ( p q1 ) ( p q m )
Ф( p )
n
n 1
a n p a n 1 p a 0 a n ( p p1 ) ( p p n )
~
Wi ( p ) p 0 p
~
Wi ( p) p qi
qi=- i где i - вещественное положительное число
1
~
где
K
=
;
.
i
i Ti
Wi ( p) p i K i (Ti p 1)
i
qi=- i+j i и qi+1=- i-j i
(11)
где i и i - вещественные
положительные числа
~
~
~
Wi ( p ) Wi ( p )Wi 1 ( p ) ( p i j i )( p i j i )
p 2 2 i p ( i2 i2 ) K i (Ti 2 p 2 2Ti i p 1),
любая передаточная функция Ф(p) рационального вида (6)
может быть представлена произведением элементарных
сомножителей рационального вида (7-12)
(12)

29.

Элементарные динамические (типовые) звенья
1. W(p)=K - усилительное звено
Оператор : a0 y(t)=в0 x(t) или y(t)=K x(t),
в0
- параметр звена, называемый коэффициентом усиления
K
a0
K
2. W ( p )
p
- интегрирующее звено
Оператор: a1 y(1)(t)=в0 x(t) или
в0
K
a1
t
y (t ) K x( )d
0
- коэффициент усиления

30.

3.
K
W( p )
Tp 1
- апериодическое или инерционное
звено (стандартная форма записи) с
параметрами К и Т.
Оператор: a1 y(1)(t)+a0 y(t)=в0 x(t) или Ty(1)(t)+y(t)=K x(t).
К=в0 /а0 – коэффициент усиления, Т=а1 /а0 – постоянная
времени
4.
K
инерционное звено второго
порядка - первая
T 2 p 2 2T p 1
стандартная форма записи.
Параметры звена: К - коэффициент усиления; Т- постоянная
времени; - коэффициент затухания (демпфирования)
W( p )
Оператор инерционного звена второго порядка:
a2y(2)(t)+ a1y(1)+a0y(t)=в0x(t) или T2y(2)(t)+2Tξy(1)(t)+y(t)=KX(t).
a1
в0
a2
K ;
T
;
Величины T>0 и 0
2 a2 a0
а0
а0

31.

Обозначим =1/T - собственная частота звена.
W( p )
K
T p 2T p 1
2
2
W( p )
K 2
p 2 2 p 2
- вторая стандартная форма записи инерционного звена
второго порядка.
5. W(p)=K p - дифференцирующее звено.
Оператор:
a0y(t)=в1х(1)(t) или y(t)=K x(1)(t)
K
в1
- параметр звена, называемый коэффициентом усиления
а0
6. W(p)=K(Тp+1) - форсирующее звено (стандартная форма
записи) К - коэффициент усиления; Т- постоянная времени.
Оператор: a0y(t)=в1х(1)(t)+в0х(t) или y(t)=K[T x(1)(t)+x(t)].
K
в0
а0
Т=в1 /в0

32.

7.
W ( p) K (T 2 p2 2T p 1)
– форсирующее звено второго порядка (стандартная форма
записи)
К - коэффициент усиления, Т - постоянная времени, коэффициент затухания (демпфирования)
Оператор звена имеет вид:
a0y(t)=в2х(2)(t)+ в1х(1)(t)+в0х(t) или y(t)=K[T2x(2)(t)+2Tξx(1)(t)+x(t)]
в0
K ;
а0
в2
T
;
в0
в1
2 в2 в0
8. W(p)=K e-p
- звено постоянного запаздывания
при К=1 W(p)=e-p – звено чистого запаздывания
Совокупность вышеперечисленных идеальных динамических
звеньев часто называют функционально полным набором
элементов автоматики.

33.

.
Следующие звенья не являются элементарными в полном
смысле этого слова, но их часто относят к типовым в силу
их широкого распространения
Реальное дифференцирующее звено
KTp
W ( p)
Tp 1
Интегральное звено с замедлением
W ( p)
K
p(Tp 1)
Пропорционально-интегральное звено
1
W ( p)
K
Tp

34.

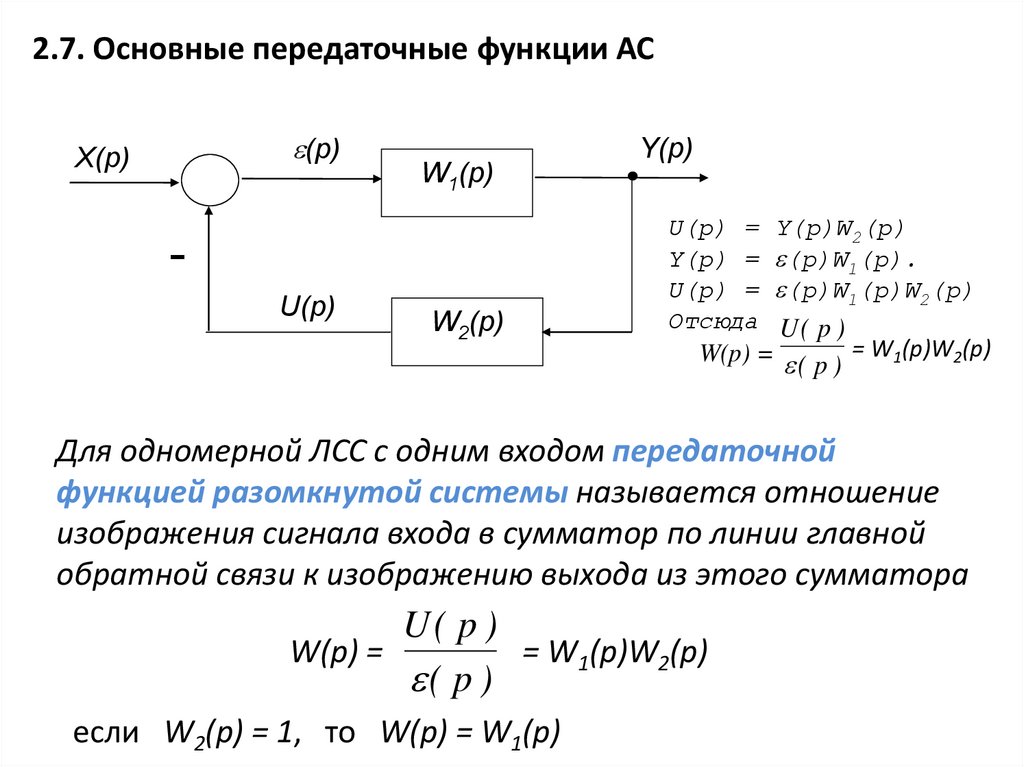
2.7. Основные передаточные функции АС
(p)
X(p)
W1(р)
U(p)
W2(р)
Y(p)
U(p) = Y(p)W2(p)
Y(p) = (p)W1(p).
U(p) = (p)W1(p)W2(p)
Отсюда U ( p )
W(p) = ( p ) = W1(p)W2(p)
Для одномерной ЛСС с одним входом передаточной
функцией разомкнутой системы называется отношение
изображения сигнала входа в сумматор по линии главной
обратной связи к изображению выхода из этого сумматора
U( p )
W(p) =
= W1(p)W2(p)
( p )
если W2(p) = 1, то W(p) = W1(p)

35.

Y
(
p
)
Передаточную функцию W1(p) =
( p)
называют передаточной функцией прямого тракта.
Передаточной функцией замкнутой АС называется
отношение изображения выходного сигнала к изображению
входного сигнала системы:
W1 ( p )
Y( p )
Ф(p) =
X ( p ) 1 W( p )
1. Если W2(p) = 1, т.е. АС с ЖОС, то Yж(p)
= X(p) и у следящей системы понятия
передаточных функций прямого тракта
и разомкнутой системы идентичны.
W1(p)=
Q( p )
P( p )
W(p) = W1(p)W2(p)
(p)
X(p)
W1(р)
U(p)
W2(р)
W1 ( p)
B( p)
Q( P )
Ф(p)= A( p) 1 W ( p) Q( p) Р( p)
1
для следящей системы полиномы числителей замкнутой и разомкнутой АС
совпадают; характеристический полином замкнутой системы A(p) = Q(p)+P(p)
Y(p)

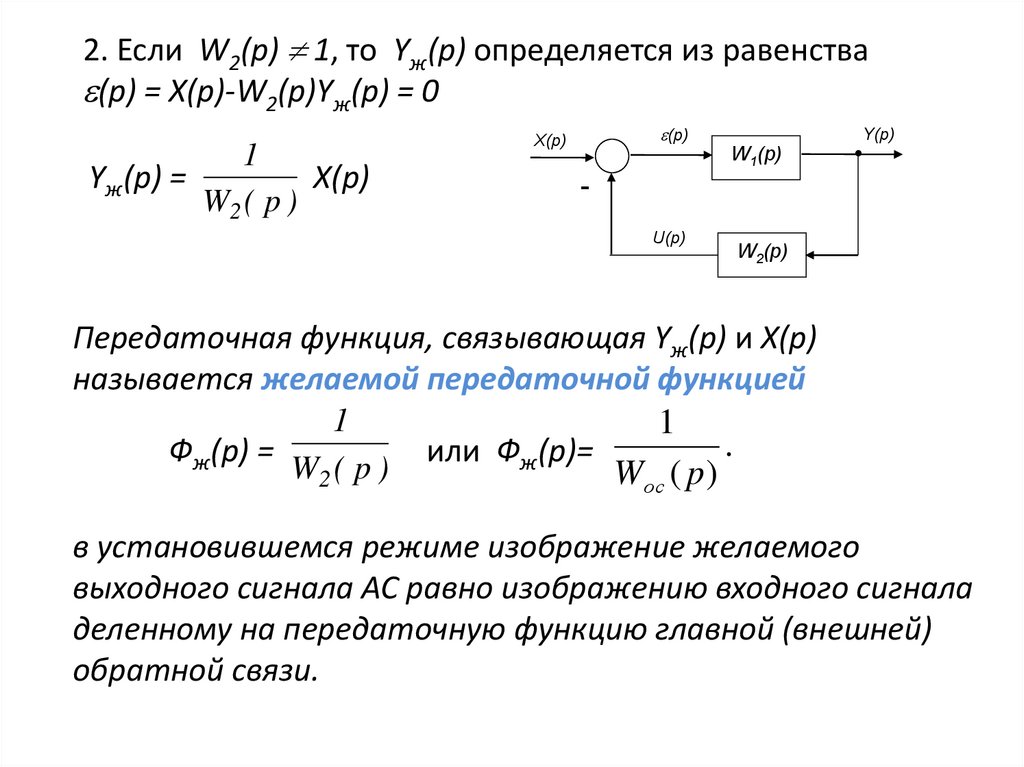
36.

2. Если W2(p) 1, то Yж(p) определяется из равенства
(p) = X(p)-W2(p)Yж(p) = 0
1
Yж(p) =
X(p)
W2 ( p )
(p)
X(p)
W1(р)
Y(p)
U(p)
W2(р)
Передаточная функция, связывающая Yж(p) и X(p)
называется желаемой передаточной функцией
1
1
.
Фж(p) =
или Фж(р)=
W2 ( p )
Wос ( p )
в установившемся режиме изображение желаемого
выходного сигнала АС равно изображению входного сигнала
деленному на передаточную функцию главной (внешней)
обратной связи.

37.

Ошибка отработки системой задающего воздействия это разница между полученным и желаемым выходными
сигналами.
e(t) = y(t) – yж(t).
Для следящих систем ошибка АС определяется равенством:
e(t) = y(t) - x(t) = - (t)
Учитывая, Y(p) = X(p)Ф(p) и Yж(p) = Фж (p)X(p), ошибка системы:
E(p) = X(p)[Ф(p) – Фж(p)]
Передаточной функцией АС по ошибке называется
отношение изображения сигнала ошибки к изображению
входного сигнала системы:
E( p )
ФЕХ(p) =
= Ф(p) – Фж(p)
X( p )
Для следящей системы Фж(p) = 1
W(p) - передаточная функция
разомкнутой системы.
W( P )
1
1
ФЕХ(p) = Ф(p) -1 = 1 W ( p )
1 W( p )

38.

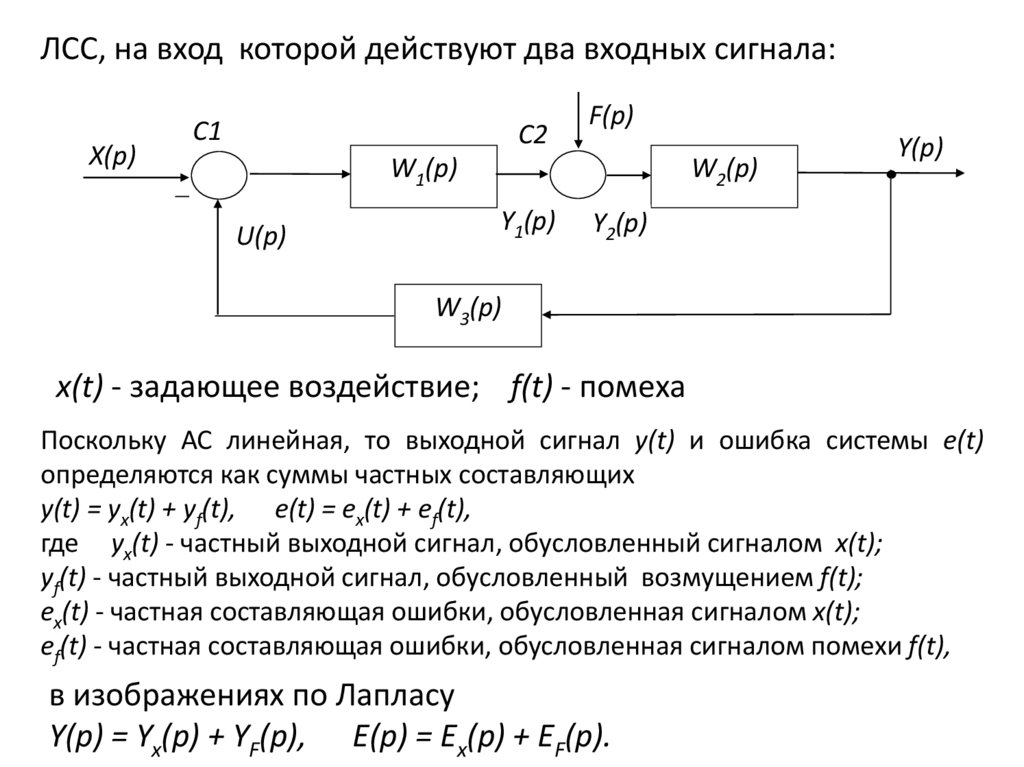
ЛСС, на вход которой действуют два входных сигнала:
X(p)
C1
C2
F(p)
W1(р)
U(p)
W2(р)
Y1(p)
Y(p)
Y2(p)
W3(р)
x(t) - задающее воздействие; f(t) - помеха
Поскольку АС линейная, то выходной сигнал y(t) и ошибка системы e(t)
определяются как суммы частных составляющих
y(t) = yx(t) + yf(t), e(t) = ex(t) + ef(t),
где yx(t) - частный выходной сигнал, обусловленный сигналом x(t);
yf(t) - частный выходной сигнал, обусловленный возмущением f(t);
ex(t) - частная составляющая ошибки, обусловленная сигналом x(t);
ef(t) - частная составляющая ошибки, обусловленная сигналом помехи f(t),
в изображениях по Лапласу
Y(p) = Yx(p) + YF(p), E(p) = Ex(p) + EF(p).

39.

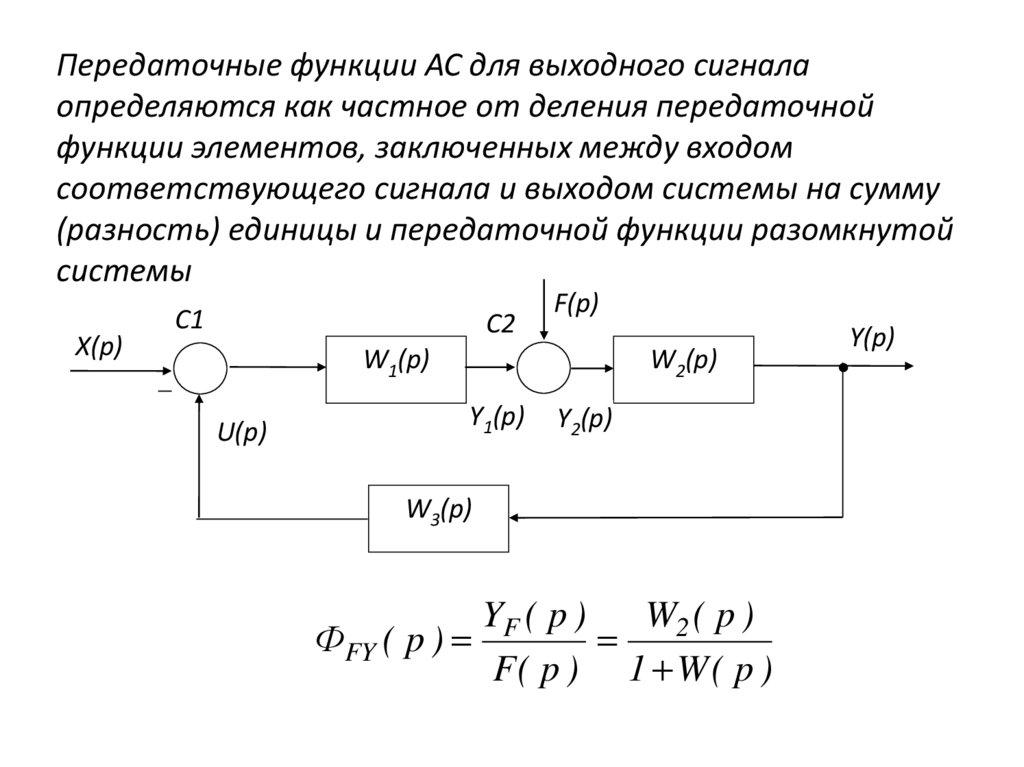
Передаточные функции АС для выходного сигнала
определяются как частное от деления передаточной
функции элементов, заключенных между входом
соответствующего сигнала и выходом системы на сумму
(разность) единицы и передаточной функции разомкнутой
системы
X(p)
C1
C2
F(p)
W1(р)
U(p)
W2(р)
Y1(p)
Y2(p)
W3(р)
YF ( p )
W2 ( p )
ФFY ( p )
F( p ) 1 W ( p )
Y(p)

40.

X(p)
.
C1
C2
F(p)
W1(р)
Y1(p)
U(p)
Y(p)
W2(р)
Y2(p)
W3(р)
Передаточные функции для ошибки E(p) определяются как отношение
изображения той части ошибки, которая обусловлена соответствующим
входным сигналом, к изображению входного сигнала:
ФXE(p) =
EX ( p )
X( p )
ФFE(p) =
EF ( p )
F( p )
E(p) = Y(p)-Yж (p)
Y(p)=ФXY(p)X(p)+ФFY(p)F(p)
Yж(р)=Фж(р)Х(р)
E(p) = [ФXY (p)-Фж(p)]X(p) + ФFY (p)F(p)
E(p) = Ex(p) + EF(p)
1
Фж ( р )
W3 ( p )
EX (p) = [ФXY (p)-Фж(p)]X(p) и EF(p) = ФFY (p)F(p)
1
ФXE (p)=Ф(p )- W ( p )
3
ФFE (p) = ФFY (p)

41.

Лайков, М.И. Автоматика и управление. Часть 1 - Иркутск:
МГТУ ГА, 2010. с. 31-43, с. 44-53, 55-67