Построение графиков тригонометрических функций y=sinx и y=cosx

1.

Построение графиков
тригонометрических
функций
y=sinx и y=cosx

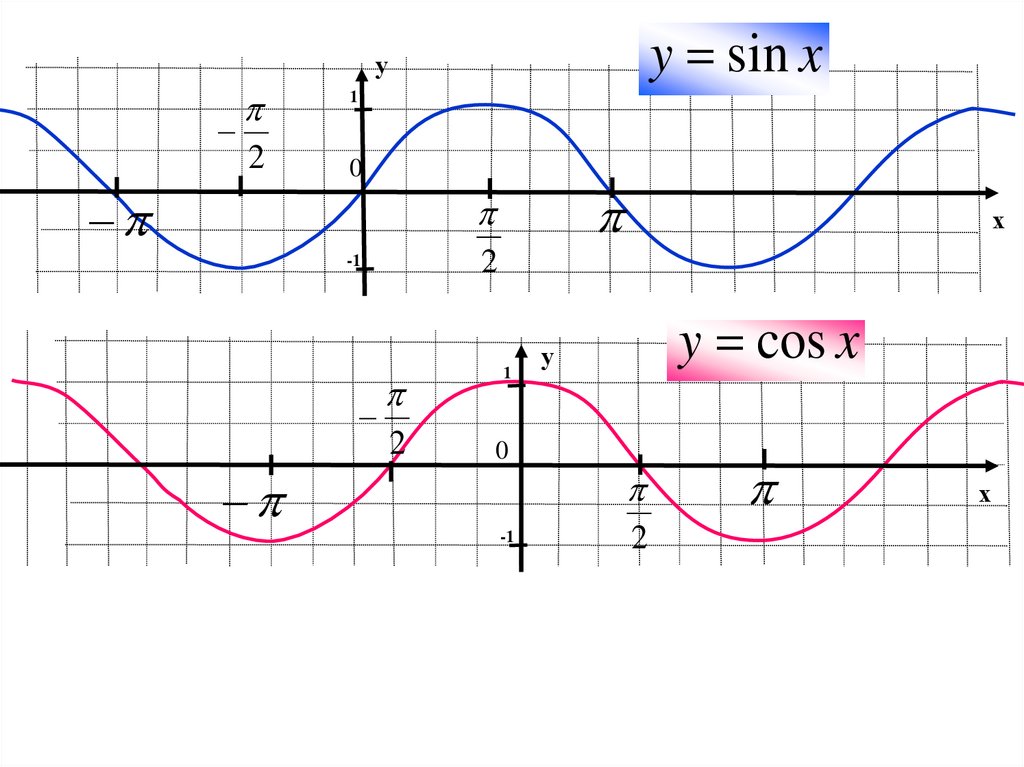
2. y= sin x

Свойство 1.
Область определения –
множество R всех действительных чисел:
D(f) = (- ∞; + ∞)

3. y= sin x

Свойство 2.
Так как
sin (-x) = - sin x, то
y = sin x –
нечётная функция,
значит её график симметричен
относительно
начала координат.

4. y= sin x

Свойство 3.
Функция у = возрастает на отрезке
[0; π/2]
и убывает на отрезке [π/2; π].
π/2
π
0

5. y= sin x

Свойство 4.
Функция у =sin x
ограничена и снизу, и сверху:
- 1 ≤ sin x ≤ 1

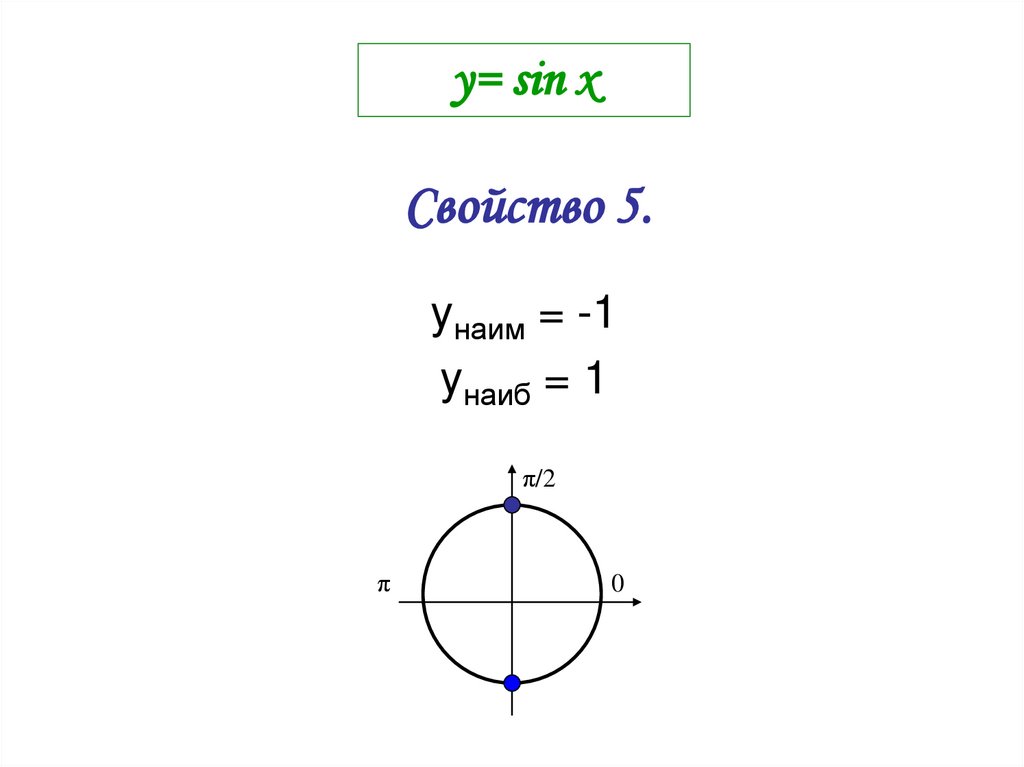
6. y= sin x

Свойство 5.
yнаим = -1
yнаиб = 1
π/2
π
0

7.

Построим график функции
y = sin x в прямоугольной
системе координат Оху.

8.

у
0
π/2
π
х

9. Сначала построим часть графика на отрезке [0; π] .

Теперь
построим
часть
графика
на
Таким образом
весь
график
представляет
Сначала
построим
часть
графика
наотрезке
отрезке
На
на0 отрезке
отрезке
[π;
[-2π;
2π]-π]
график
график
функции
функции
x Асобой
π/6
π/3
π/2
2π/3
5π/6
π
[-π;
0],
непрерывную
которую
[0; π]линию,
.
выглядит
выглядит
опять
так:
вот так:у=sin x .
учитывая
нечётность
функции
y
0
1/2 √3/2синусоидой.
1
√3/2 1/2
0
называют
У
1
-2π
-3π/2
-π
-π/2
π/2
0
π
-1
Полуволна
Арка
синусоиды
синусоиды
3π/2
2π
Х

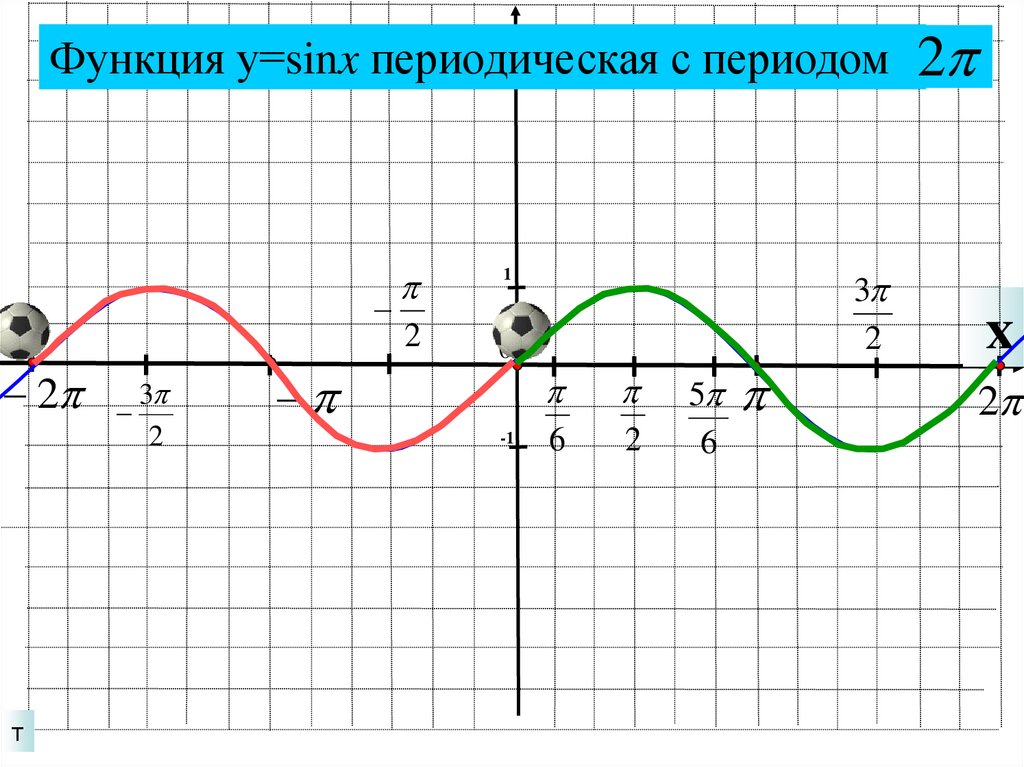
10.

Функция у=sinx периодическая с периодом
2
2
т
3
2
3
2
1
0
-1
6
2
5
6
2
x
2

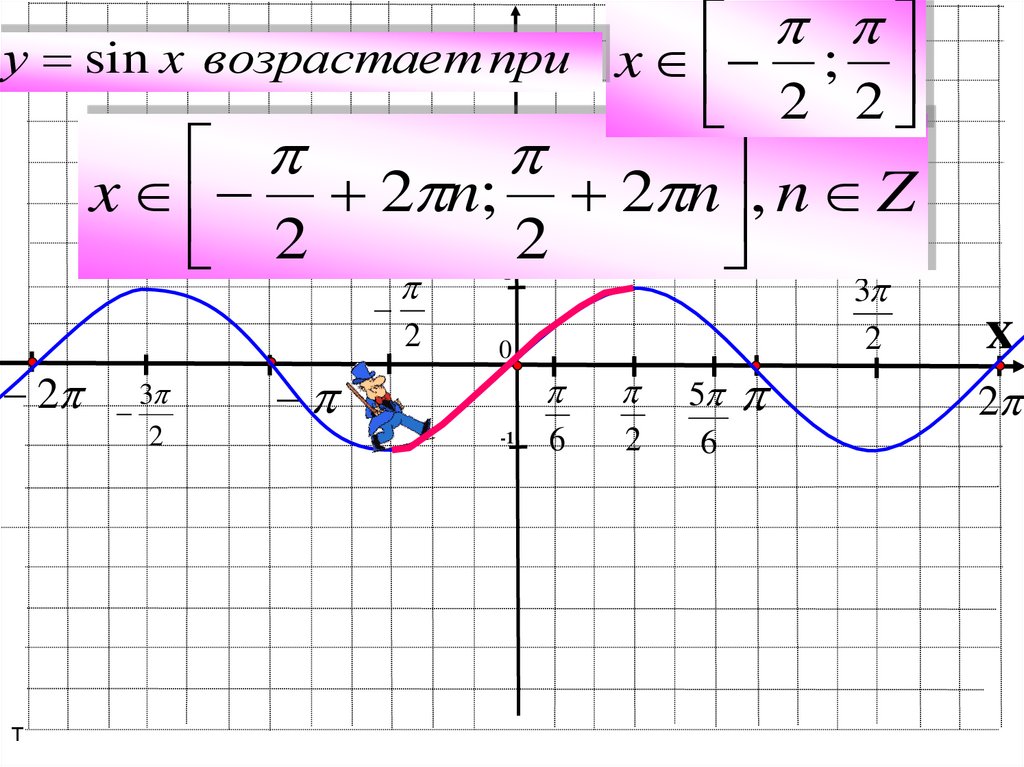
11.

y
у sin x возрастает при x ;
2 2
x 2 n; 2 n , n Z
2
2
2
2
т
3
2
3
2
1
0
-1
6
2
5
6
x
2

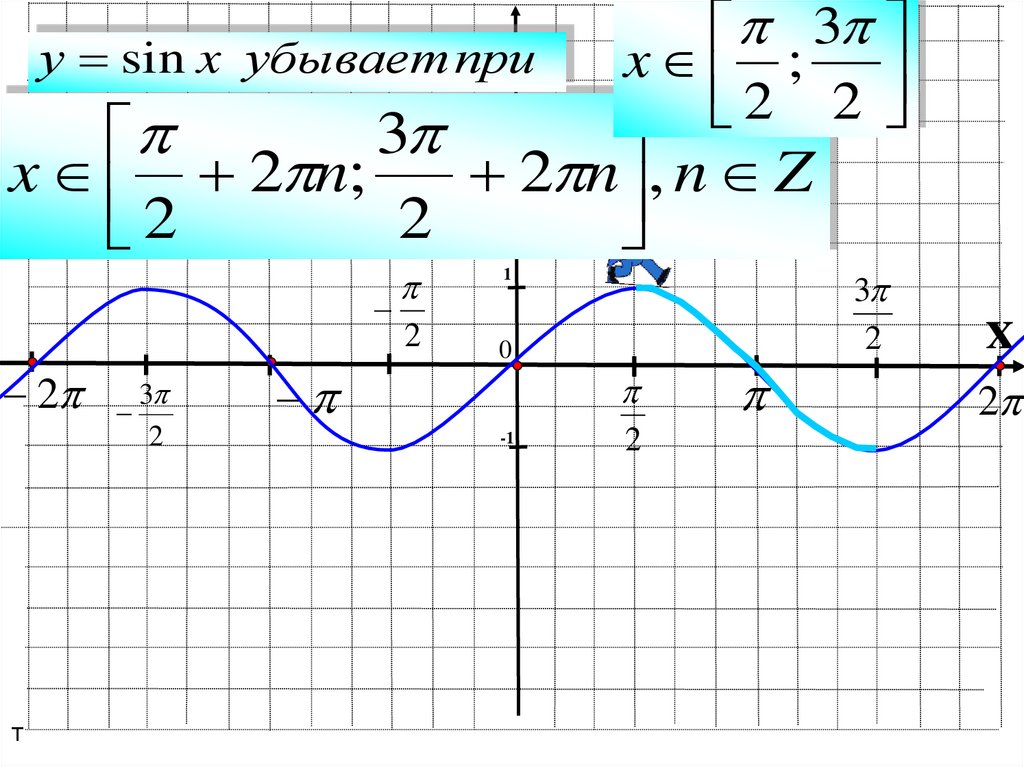
12.

y
у sin x убывает при
3
x ;
2 2
3
x 2 n;
2 n , n Z
2
2
2
2
т
3
2
3
2
1
0
-1
2
x
2

13.

Построение графика
функции у=cosx

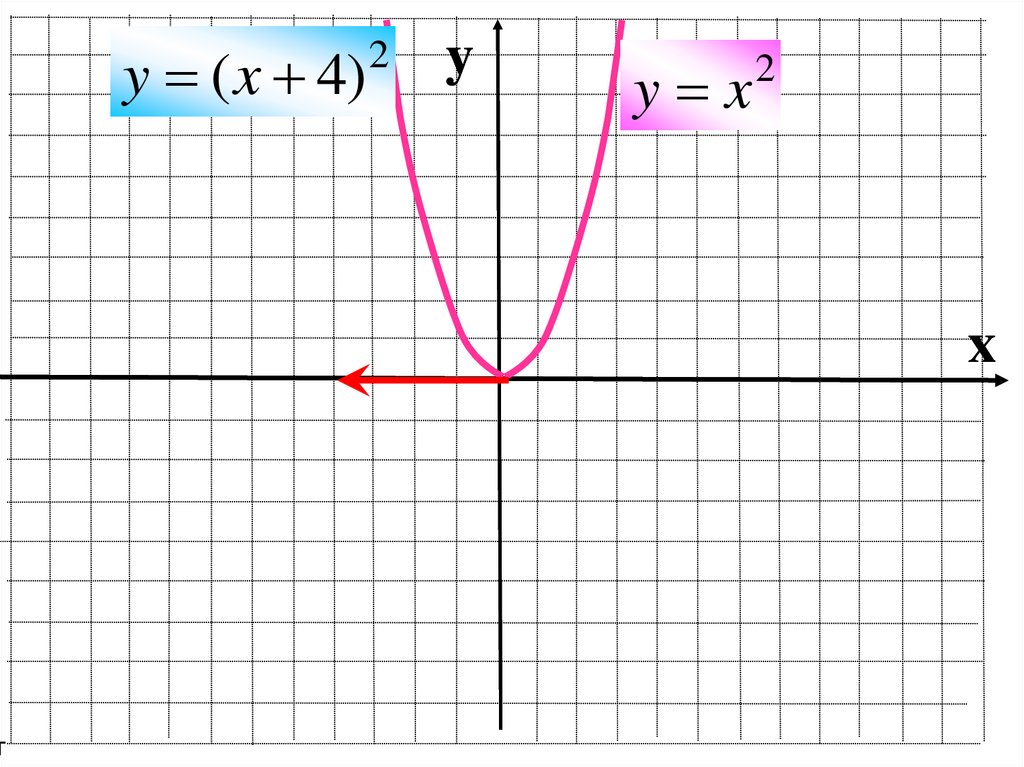
14.

т
y ( x 4)
2
y
y x
2
x

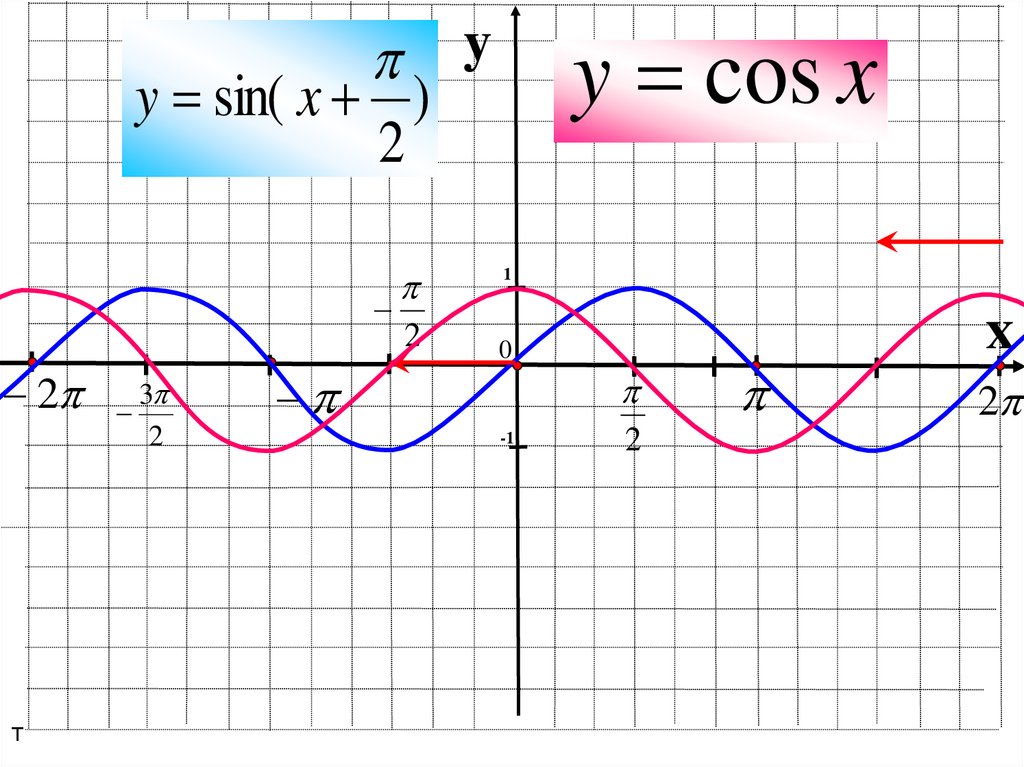
15.

y cos x
y
y sin( x )
2
2
2
т
3
2
1
0
-1
2
x
2

16.

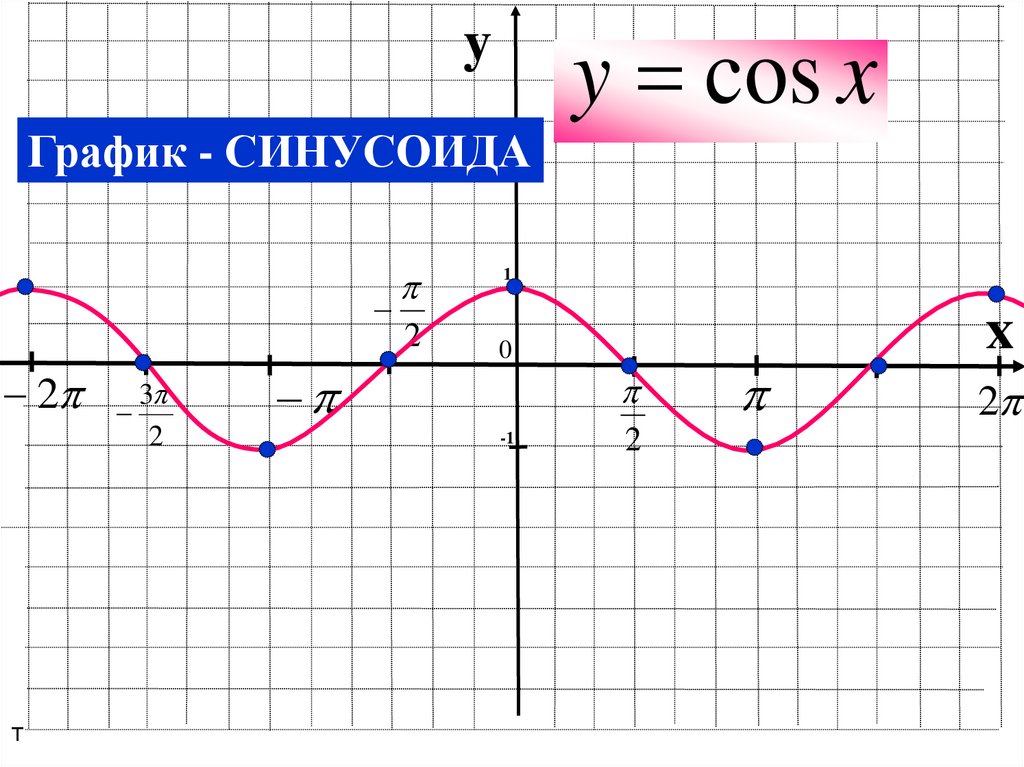
y cos x
y
График - СИНУСОИДА
2
2
т
3
2
1
0
-1
2
x
2

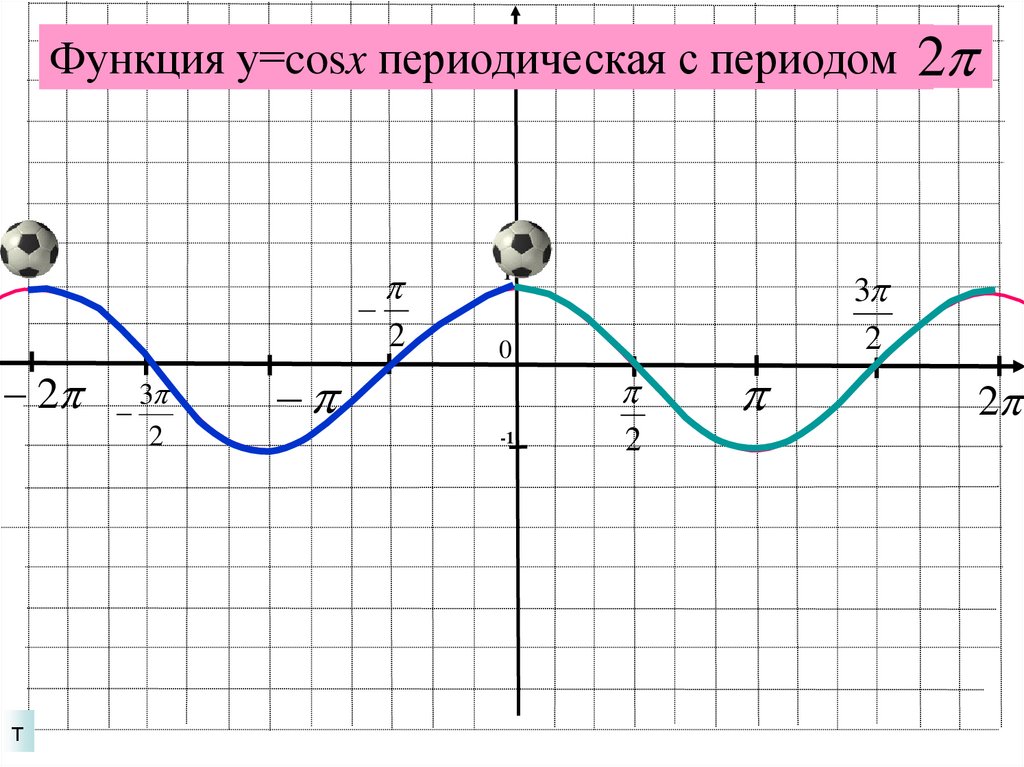
17.

Функция у=cosx периодическая с периодом
2
2
т
3
2
3
2
1
0
-1
2
2
2

18.

3
2
1 y
2
-1
2
3
2
x
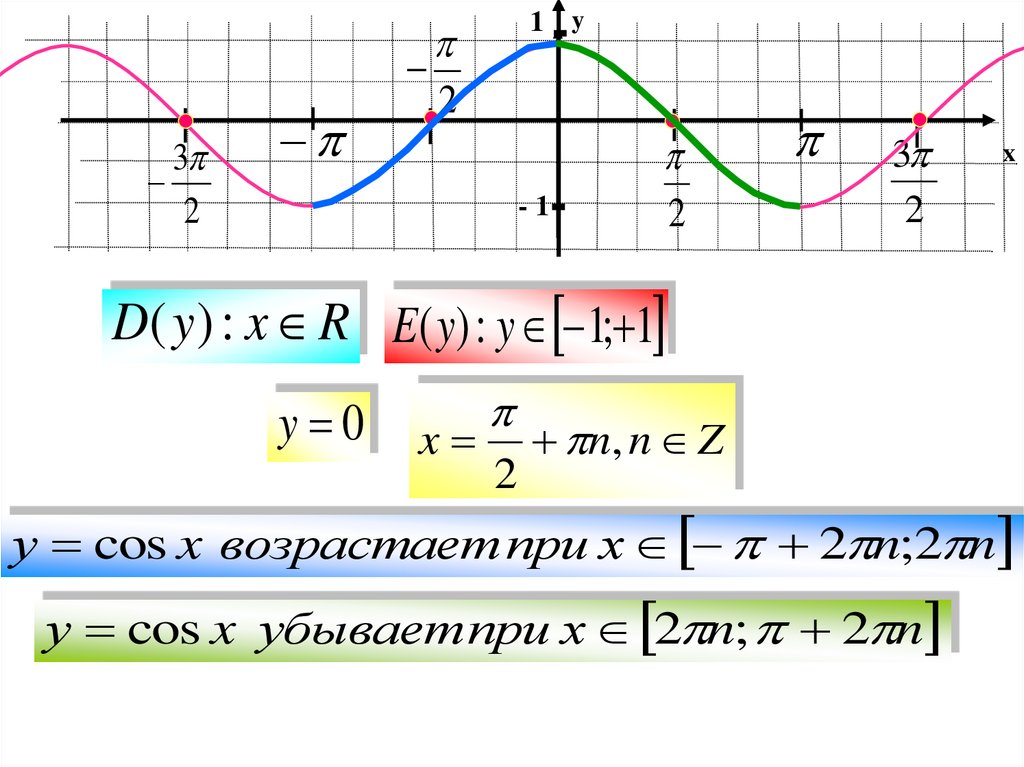
D( y ) : x R E( y) : y 1; 1
y 0
x
2
n, n Z
у cos x возрастает при х 2 n;2 n
у cos x убывает при х 2 n; 2 n

19.

y sin x
3
2
-1
y cos x
3
2
2
1 y
2
2
3
2
x
1 y
-1
2
3
2
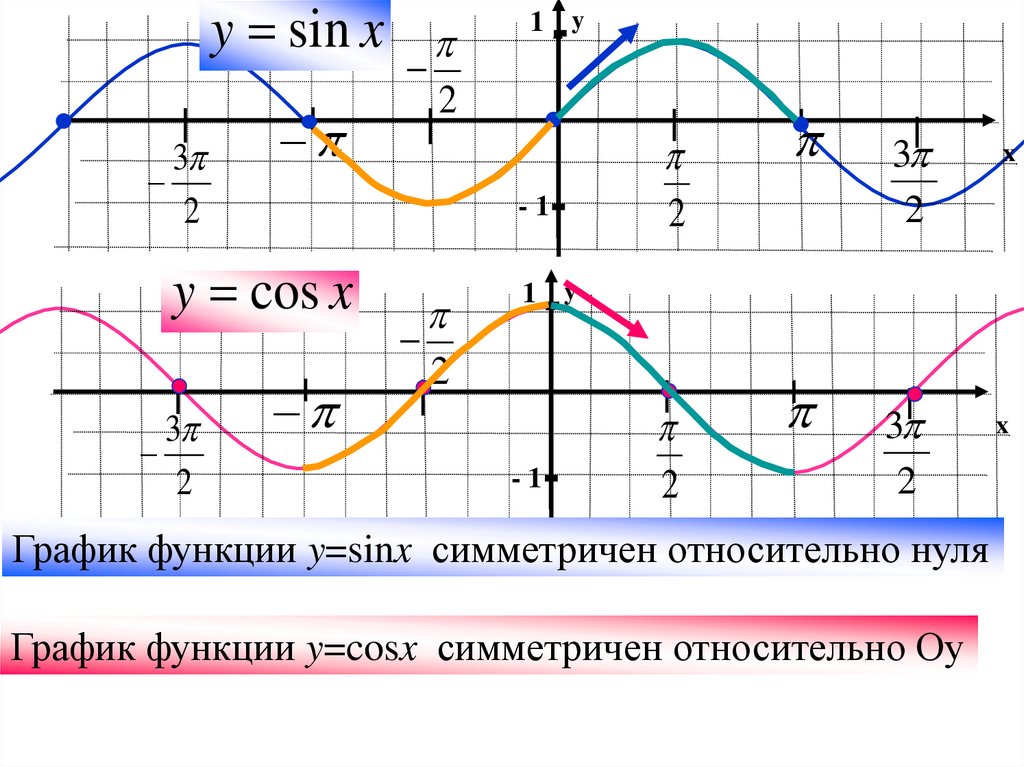
График функции y=sinx симметричен относительно нуля
График функции y=cosx симметричен относительно Оу
x

20.

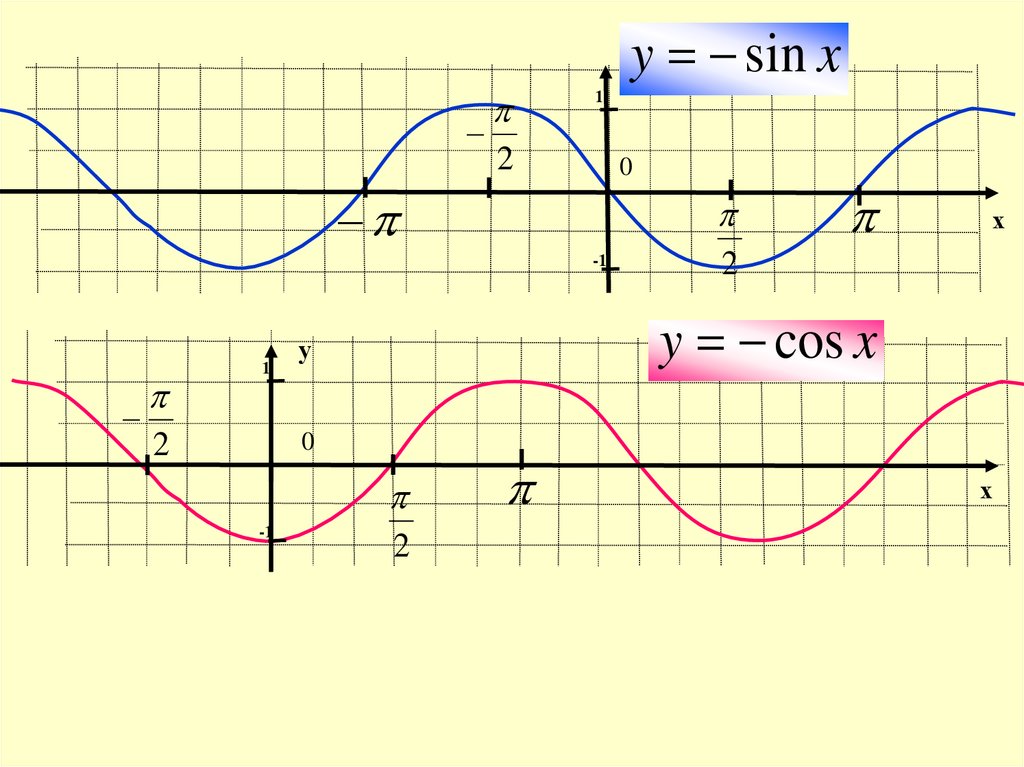
y sin x
у
2
1
0
-1
2
2
1
х
y cos x
у
0
-1
2
х

21.

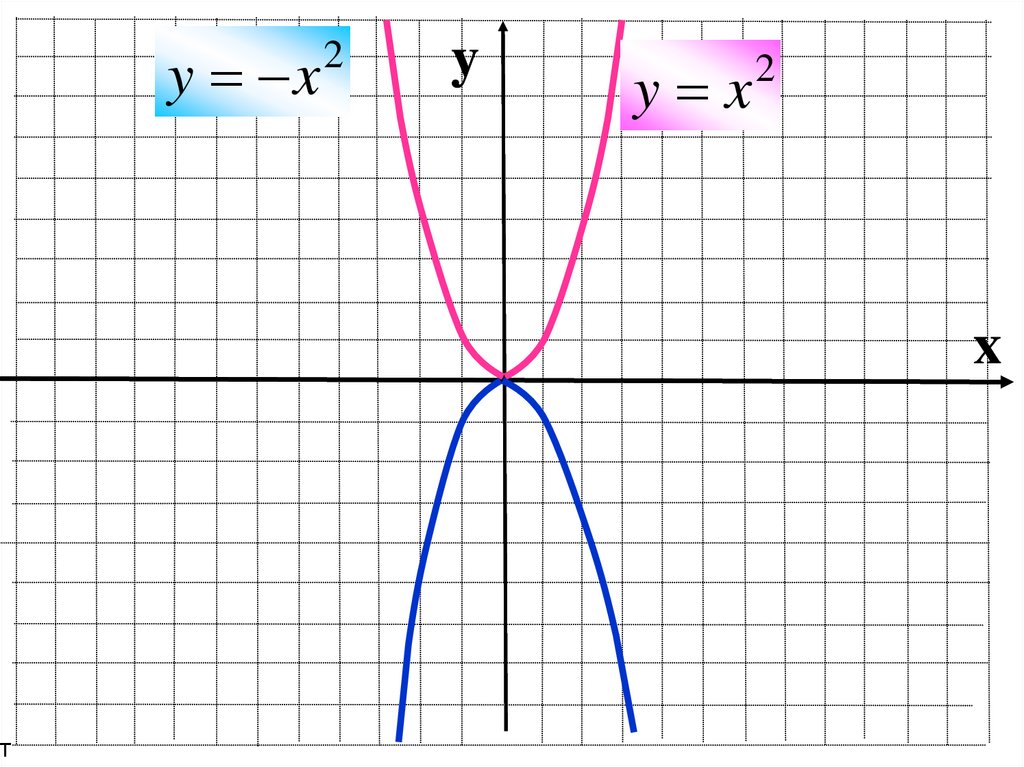
y x
2
y
y x
2
x
т

22.

y sin x
2
у
1
0
-1
2
1
х
y cos x
у
0
-1
2
2
х

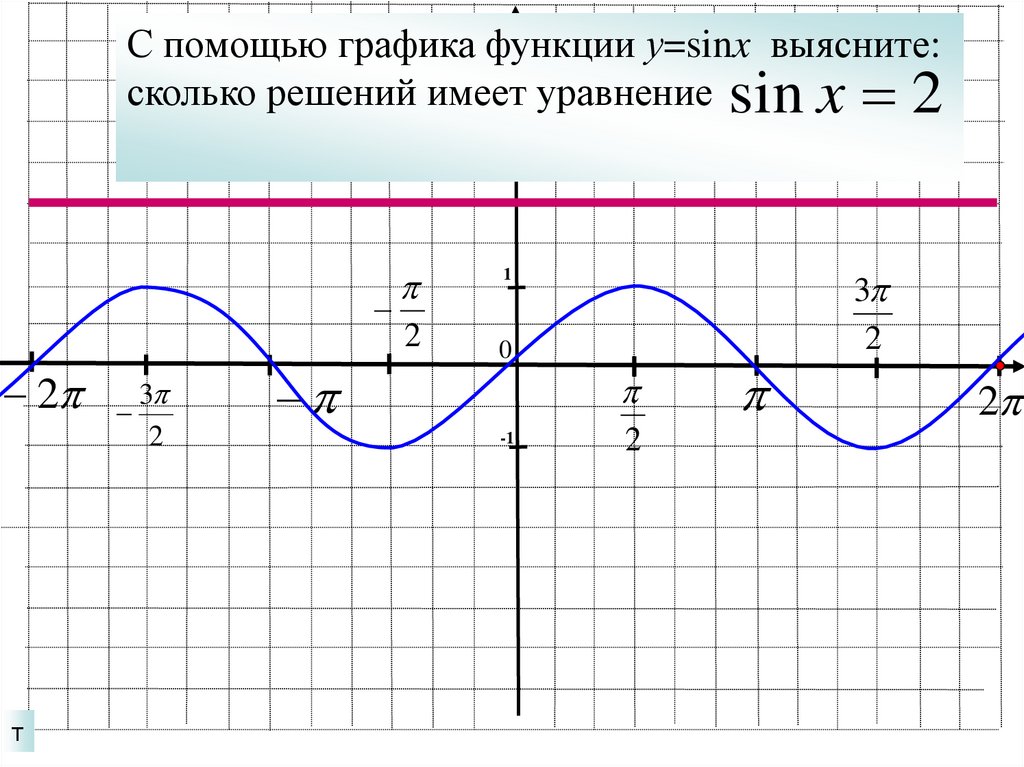
23.

С помощью графика функции у=sinx выясните:
сколько решений имеет уравнение sin x 2
2
2
т
3
2
3
2
1
0
-1
2
2

24.

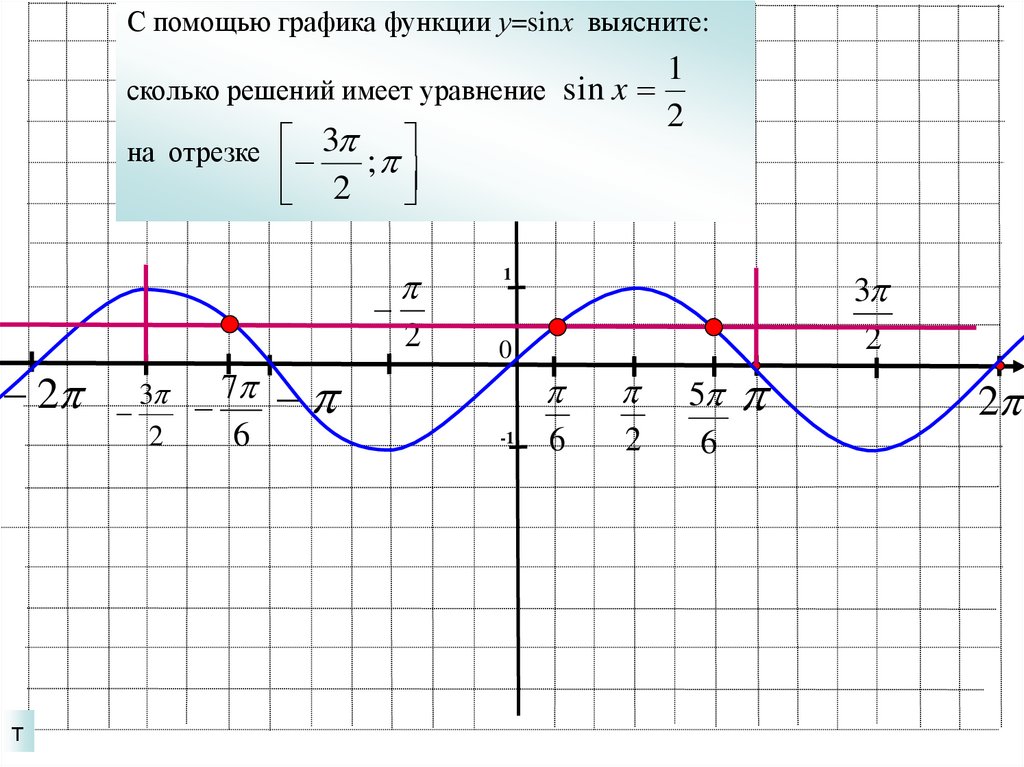
С помощью графика функции у=sinx выясните:
сколько решений имеет уравнение sin x
на отрезке
3
2 ;
2
2
т
7
3
2
6
1
2
3
2
1
0
-1
6
2
5
6
2

25.

Движение по синусоиде

26.

27.

28.

29.

30.

Научись встречать беду не плача:
Горький миг - не зрелище для всех.
Знай: душа растет при неудачах
И слабеет, если скор успех.
Мудрость обретают в трудном споре.
Предначертан путь нелегкий твой
Синусоидой радости и горя,
А не верх взмывающей кривой.

31. Домашнее задание

Законспектировать материал презентации со всеми
чертежами и примерами.
Фото конспекта прислать в обсуждение «Математика».
Выучить материал по учебнику: Колмогоров А.Н. Алгебра 10-11.
Параграф 1, пункт 2, подпункты 1,2 (страницы 14-16).
Изучить материал по интернет-ресурсам
http://school-collection.edu.ru - Электронный учебник
«Математика в школе, XXI век».
http://fcior.edu.ru - информационные, тренировочные и
контрольные материалы.
www.school-collection.edu.ru - Единая коллекция цифровых
образовательных ресурсов