Построение графиков тригонометрических функций

1.

Построение графиков
тригонометрических
функций
y
x

2.

СОДЕРЖАНИЕ
1. Тригонометрические функции числового
аргумента
2. Построение графиков функций вида
y=sin(x)+m и y=cos(x)+m
3. Построение графиков функций вида
y=sin(x+t) и y=cos(x+t)
4. Построение графиков функций вида
y=A ·sin(x) и y=A ·cos(x)
5. Примеры

3. Тригонометрические функции числового аргумента.

y=sin(x)
y=cos(x)

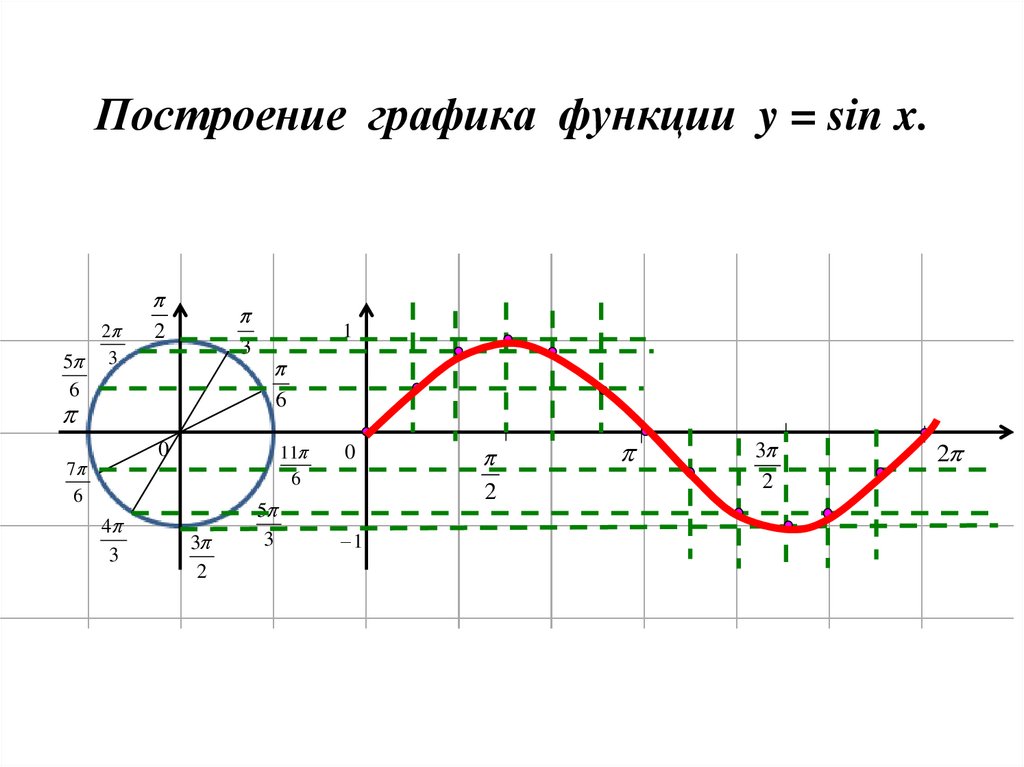
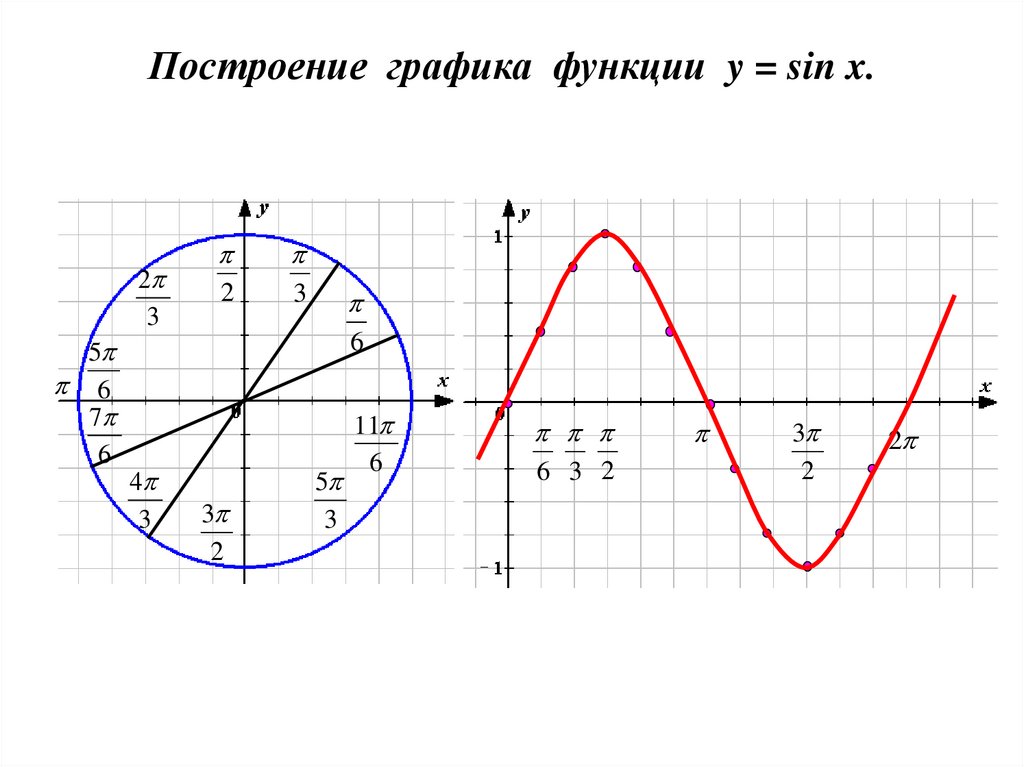
4. Построение графика функции y = sin x.

2
5 3
2
3
6
1
6
11
6
0
7
6
4
3
3
2
5
3
0
2
1
3
2
2

5.

Построение графика функции y = sin x.
2
3
2
3
6
5
6
6 3 2
3
2
3
2
2

6.

Построение графика функции y = sin x.
2
3
5
6
7
6
2
3
6
4
3
3
2
5
3
11
6
6 3 2
3
2
2

7.

Построение графика функции y = sin x.
2
3
5
6
7
6
2
3
6
4
3
3
2
5
3
11
6
6 3 2
3
2
2

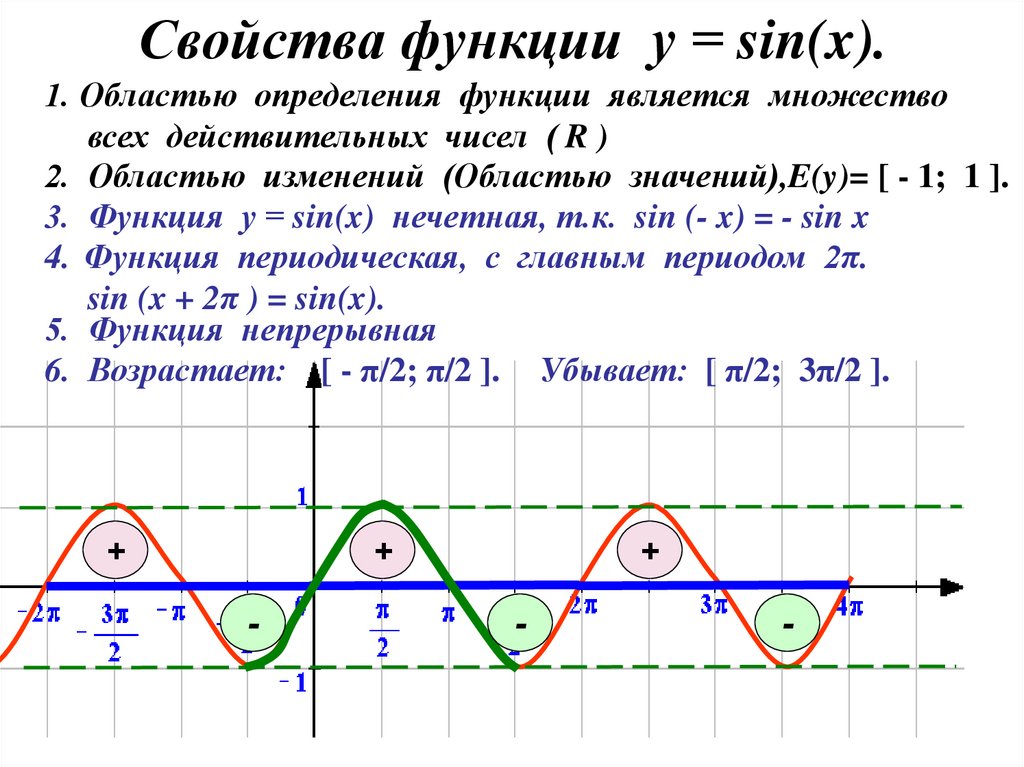
8. Свойства функции у = sin(x).

1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью изменений (Областью значений),E(y)= [ - 1; 1 ].
3. Функция у = sin(x) нечетная, т.к. sin (- x) = - sin x
4. Функция периодическая, с главным периодом 2π.
sin (x + 2π ) = sin(x).
5. Функция непрерывная
6. Возрастает: [ - π/2; π/2 ]. Убывает: [ π/2; 3π/2 ].
+
+
-
+
-
-

9.

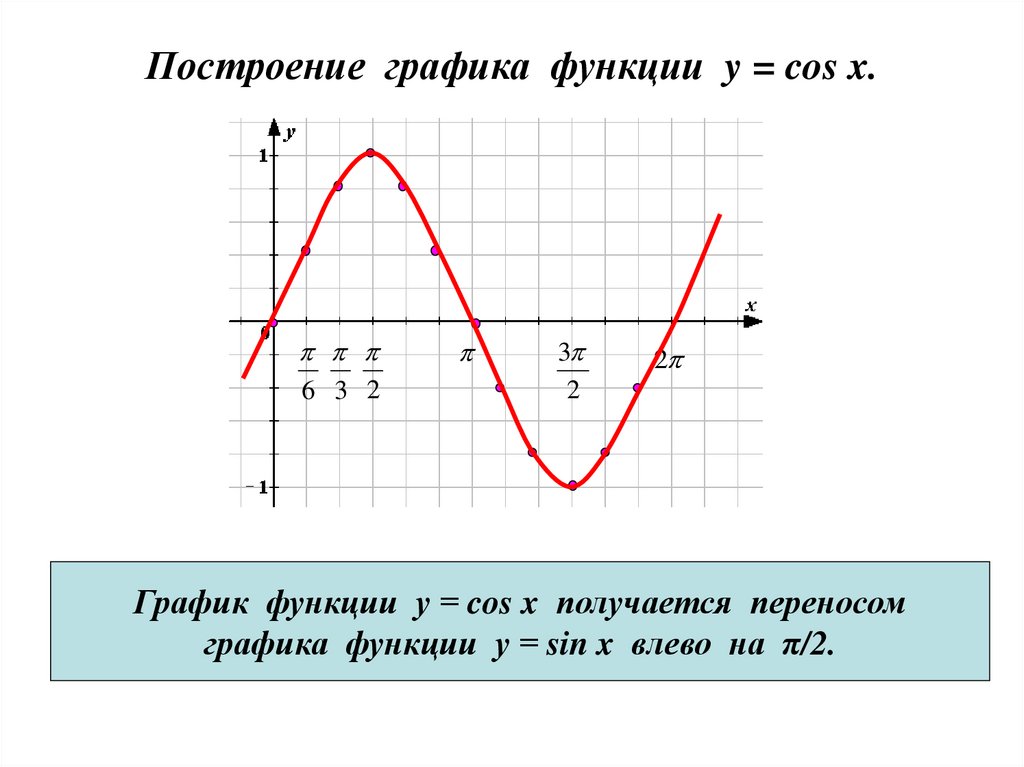
Построение графика функции y = cos x.
6 3 2
3
2
2
График функции у = cos x получается переносом
графика функции у = sin x влево на π/2.

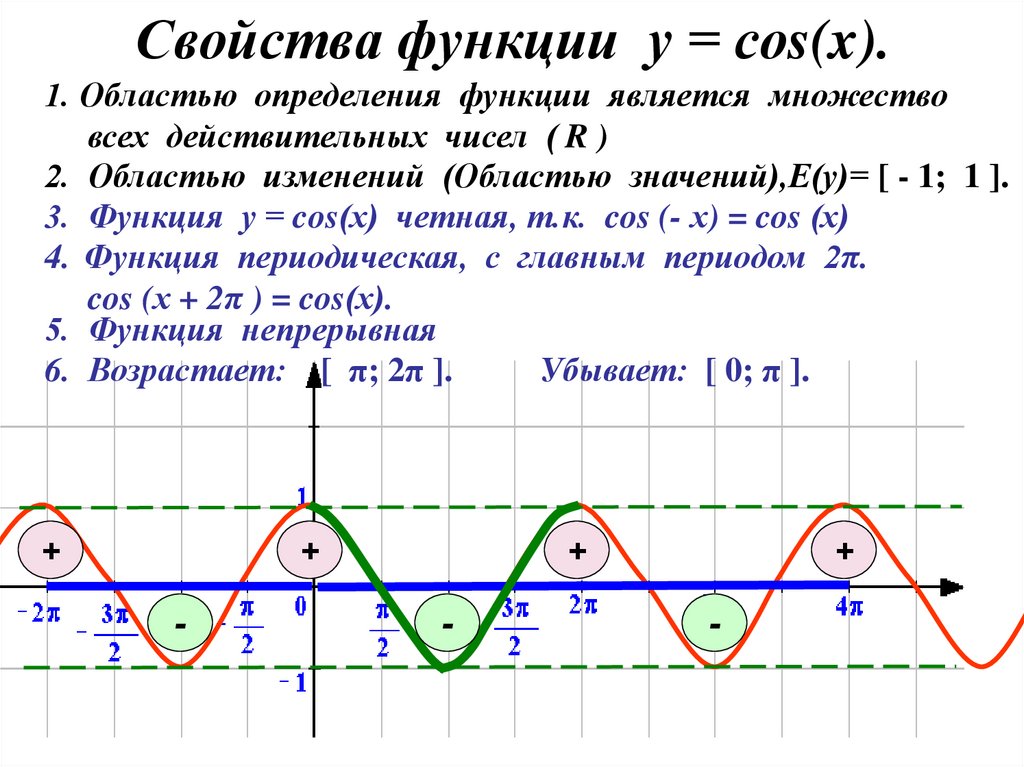
10. Свойства функции у = соs(x).

1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью изменений (Областью значений),Е(у)= [ - 1; 1 ].
3. Функция у = cos(х) четная, т.к. cos (- х) = cos (х)
4. Функция периодическая, с главным периодом 2π.
cos (х + 2π ) = cos(х).
5. Функция непрерывная
6. Возрастает: [ π; 2π ].
Убывает: [ 0; π ].
+
+
-
+
-
+
-

11.

Построение
графиков функций вида
у = sin(x) + m
и
у = cos(х) + m.

12.

Параллельный перенос
графика вдоль оси Оу
График функции y=f(x)+m
получается параллельным
переносом графика функции y=f(x),
вверх на m единиц, если m>0,
или вниз, если m<0.

13.

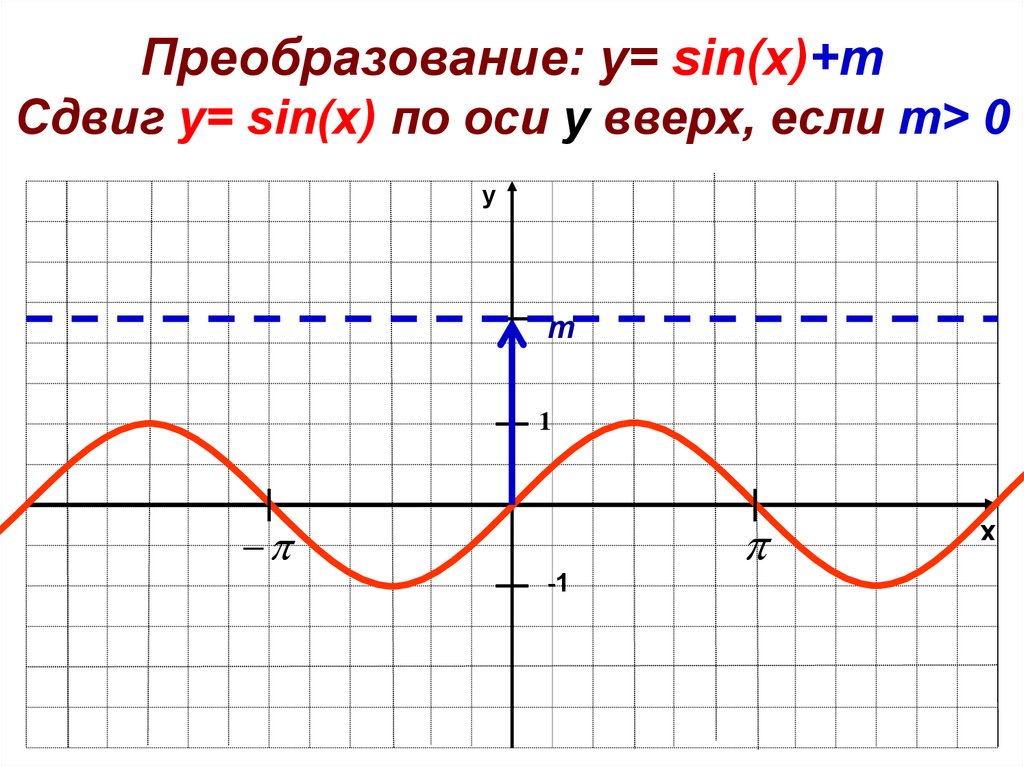
Преобразование: y= sin(x)+m
Сдвиг у= sin(x) по оси y вверх, если m> 0
y
m
1
-1
x

14.

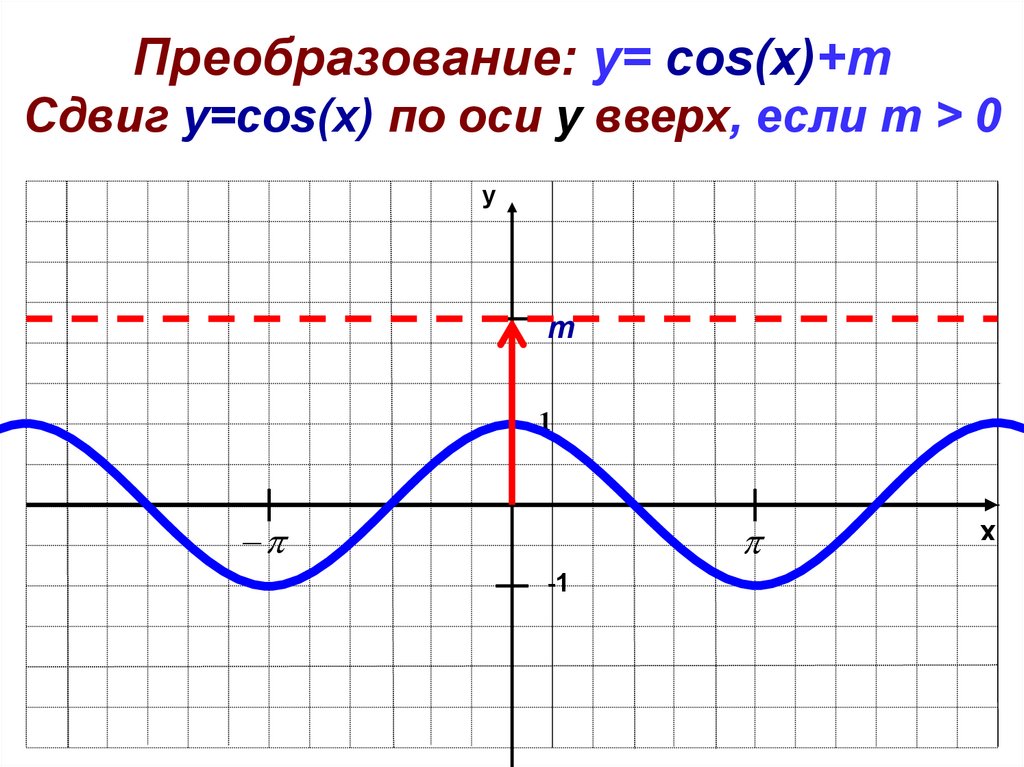
Преобразование: y= cos(x)+m
Сдвиг у=cos(x) по оси y вверх, если m > 0
y
m
1
-1
x

15.

Преобразование: y=sin(x)+m
Сдвиг у= sin(x) по оси y вниз, если m < 0
y
1
-1
m
x

16.

Преобразование: y= cos(x) + m
Сдвиг у= cos(x) по оси y вниз, если m < 0
y
1
-1
m
x

17.

Построение
графиков функций вида
у = sin( x + t )
и
у = cos( х + t )

18. Параллельный перенос графика вдоль оси Ох

График функции y = f(x + t)
получается параллельным
переносом графика функции y=f(x)
по оси х на |t| единиц масштаба
влево, если t > 0
и вправо, если t < 0.

19.

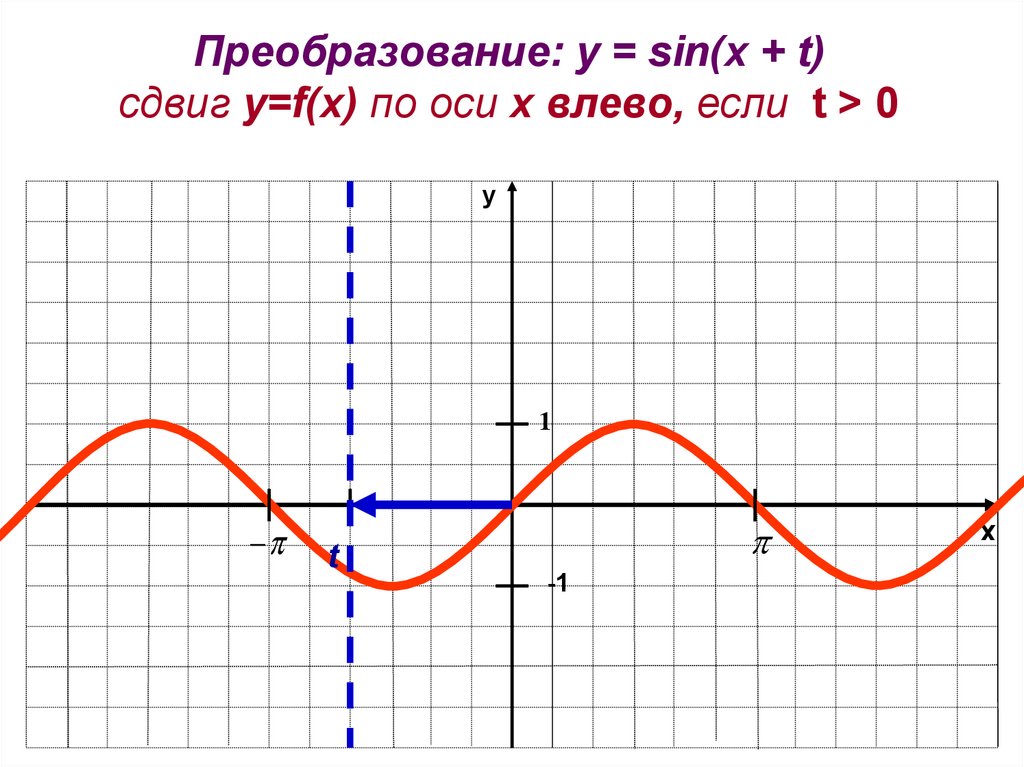
Преобразование: y = sin(x + t)
сдвиг у=f(x) по оси х влево, если t > 0
y
1
t
-1
x

20.

Преобразование: y= cos(x + t)
сдвиг у=f(x) по оси х влево, если t > 0
y
1
t
-1
x

21.

Преобразование: y= sin(x + t)
сдвиг у=f(x) по оси х вправо, если t < 0
y
1
t
-1
x

22.

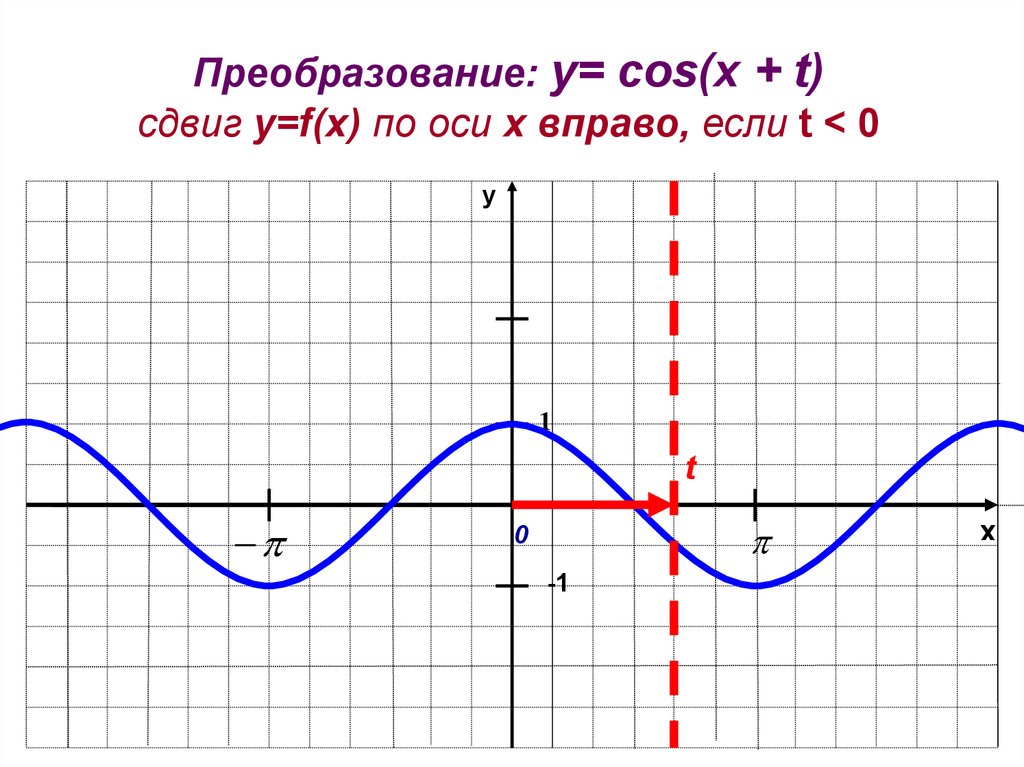
Преобразование: y= cos(x + t)
сдвиг у=f(x) по оси х вправо, если t < 0
y
1
t
0
-1
x

23. Построение графиков функций вида у = А·sin(x) и y = А·cos(x), при а > 1 и 0< а < 1

Построение графиков
функций вида
у = А·sin(x) и y = А·cos(x),
при а > 1 и 0< а < 1

24. Сжатие и растяжение вдоль оси Ох

График функции у=А·f(x) получаем
растяжением графика функции
у=f(x) с коэффициентом А вдоль
оси Ох,если А>1 и сжатием к оси
Ох с коэффициентом 0<А<1.

25.

Преобразование: y = a·sin(x), a >1
пусть а=1,5
y
1,5
1
3
2
2
-1
3 2
-1,5
3
2
x

26.

Преобразование: y = a·cos(x), a >1
пусть а=1,5
y
1,5
1
3
2
2
-1 3
-1,5
2
3
2
x

27.

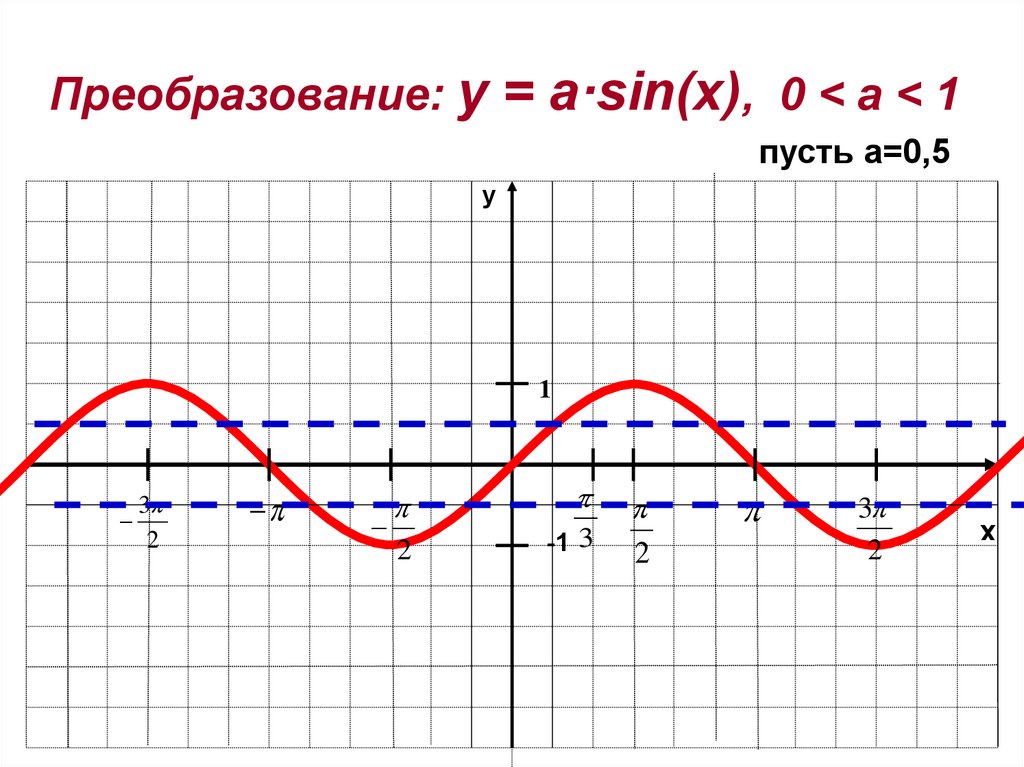
Преобразование: y = a·sin(x), 0 < a < 1
пусть а=0,5
y
1
3
2
2
-1 3
2
3
2
x

28.

Преобразование: y = a·cos(x), 0 < a < 1
пусть а=0,5
y
1
3
2
2
-1 3
2
3
2
x

29.

30.

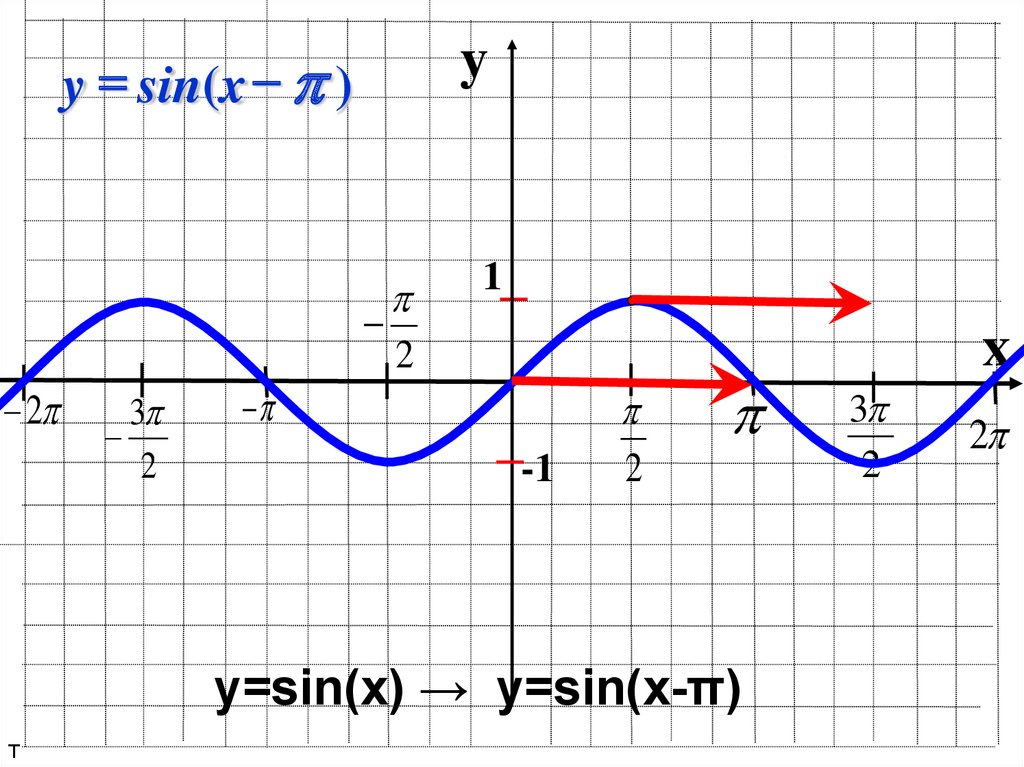
y = sin(x )
y
2
2
3
2
1
-1
2
y=sin(x) → y=sin(x-π)
т
x
3
2
2

31.

y = sin(x 2 )
2
2
у
3
2
y
1
-1
2
x
3
2
2

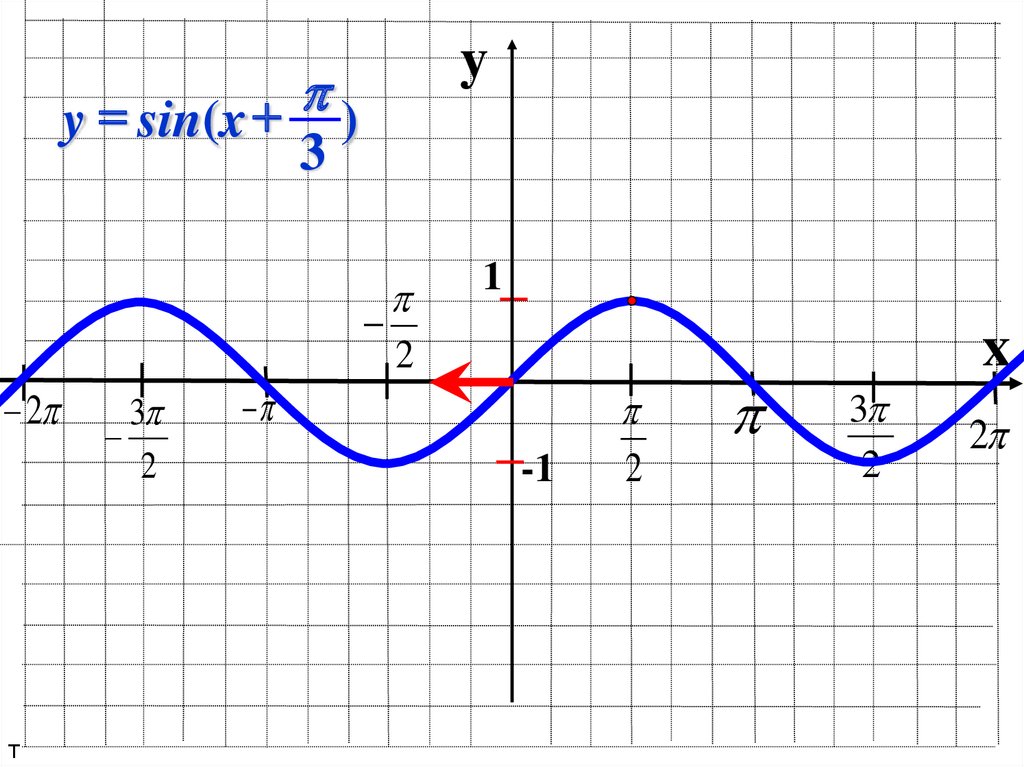
32.

y
y = sin(x + )
3
2
2
т
3
2
1
-1
2
x
3
2
2

33.

y
3
2
2
0
1
-1
2
3
2
2
5
2
y=cos(x) → y=cos(2x) → y= - cos(2x) → y= - cos(2x)+3
x

34.

x
y = sin
-2
3
y
3
2
x
y = sin x -2
3
2
0
1
-1
2
3
2
2
5
2
y=sin(x) → y=sin(x/3) → y=sin(x/3)-2
x

35.

y
3
2
2
0
1
-1
2
3
2
2
5
2
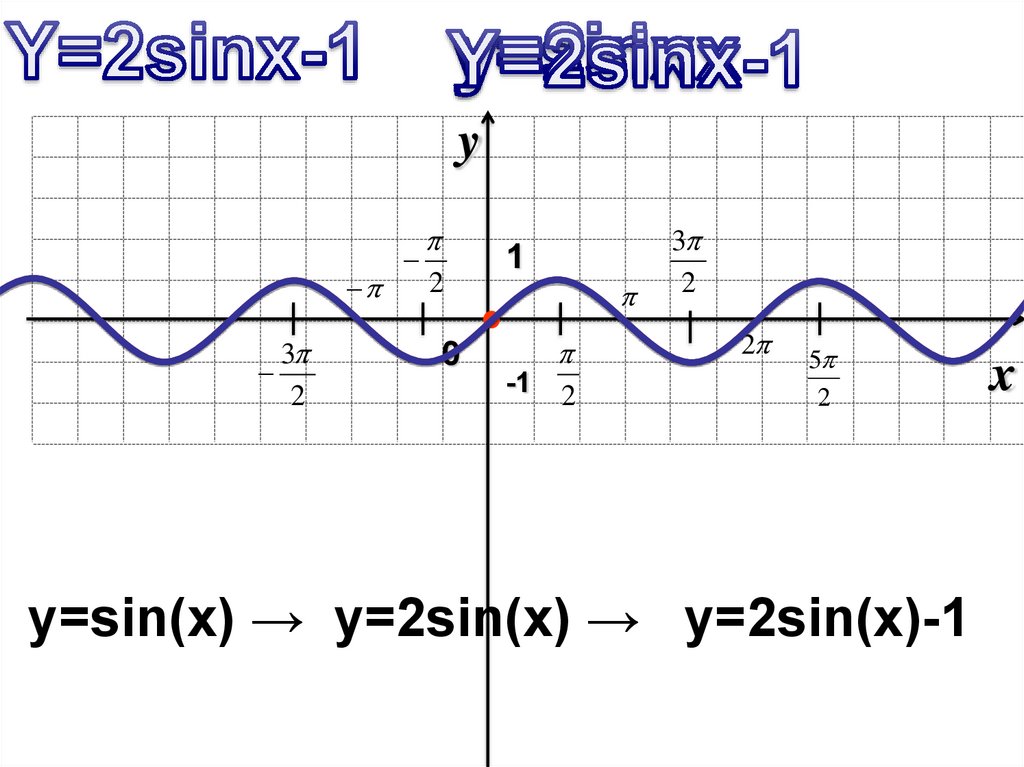
y=sin(x) → y=2sin(x) → y=2sin(x)-1
x

36.

1
y=
cosx + 2
1
1
y == =
2
y y cos x cosx + 2
22
y
3
2
2
0
1
-1
2
3
2
2
5
2
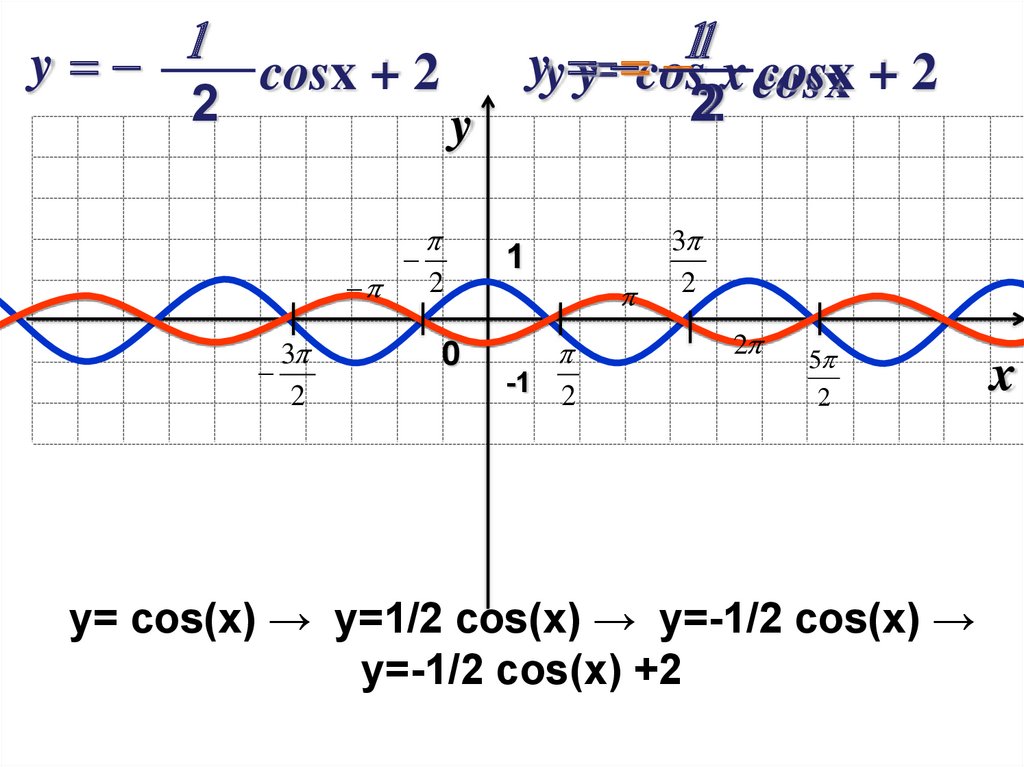
y= cos(x) → y=1/2 cos(x) → y=-1/2 cos(x) →
y=-1/2 cos(x) +2
x

37.

y
3
2
2
0
1
-1
2
3
2
2
5
2
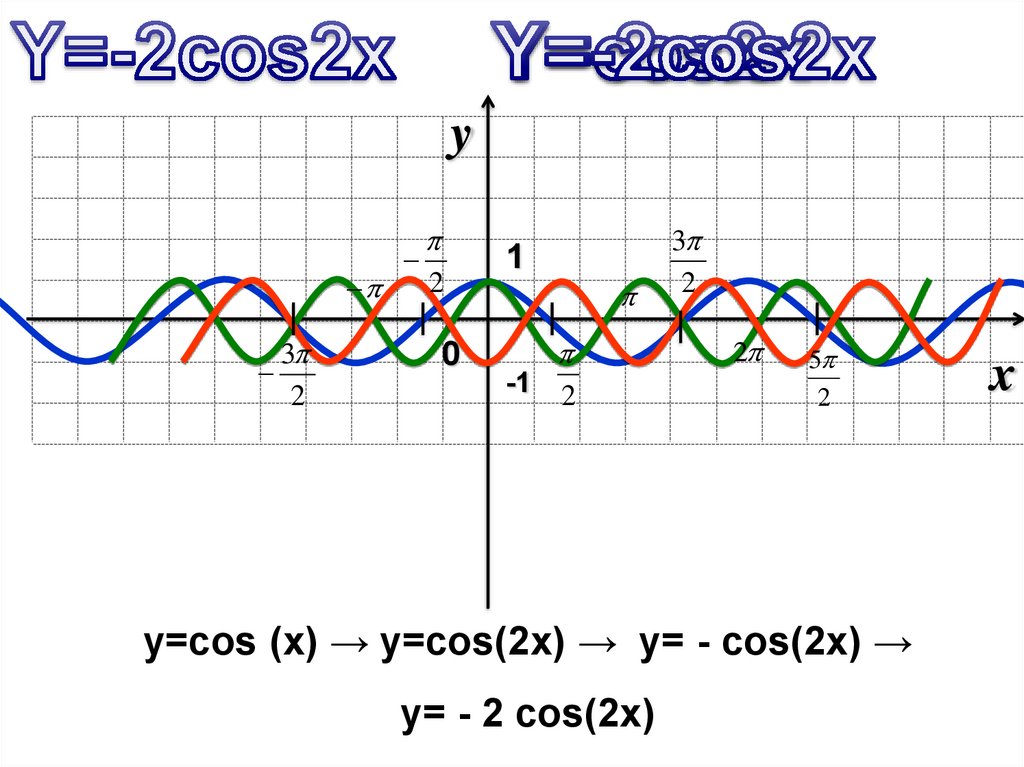
y=cos (x) → y=cos(2x) → y= - cos(2x) →
y= - 2 cos(2x)
x