Электродинамика

1. ЭЛЕКТРОДИНАМИКА

делится на 3 раздела:
- электростатику;
- электрический ток (постоянный и
переменный;
- магнитное поле.
1

2. Электростатика

изучает статические (неподвижные) заряды
и связанные с ними электрические поля.
2

3. 1. Электрический заряд

Заряды q бывают 2-х знаков «+» и «-».
Опыт: q одного знака - отталкиваются,
разноименные - притягиваются.
Милликен, 1909 г. установил:
величина заряда q любого тела кратна е:
.
где е - заряд электрона,
q = ±ne
n – целое число.

4.

Валентный е
Протоны
е = 1,6∙10-19 Кл.
Носители элементар-
ного заряда:
- электрон (q = -е),
- протон (q = +е).
Атом электр. нейтрален.
Валентные е слабо связаны с атомом и
может быть сравнительно легко (трением)
оторваны и перемещены на другое тело .
Тела с избытком е заряжены
(-), с недостатком е – (+).

5.

2. Закон сохранения зарядов
При электризации трением оба тела
заряж-ся равными по величине, но
разноименными зарядами +q и –q.
При соприкосновении тел их
заряды исчезают.
При этом суммарный q на телах не измся - происходит их перераспред-е.

6.

В замкнутой системе алгебр. сумма эл.
зарядов остается постоянной.
q
i
const
Закон сохранения
зарядов
ЗСЗ – закон фундаментальный, он
выпол-ся как для макро-, так и для
микромира.
γ - квант
Эл-н
Антинейтрино
Закон Кулона

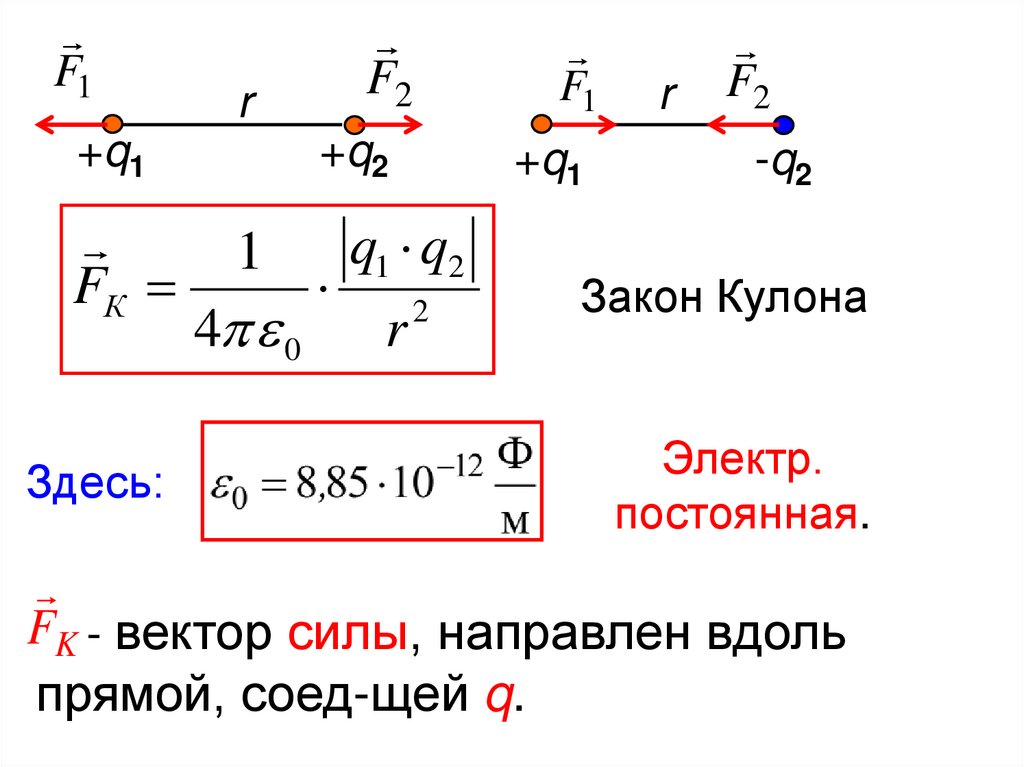
7. 3. Закон Кулона

Точечный заряд (q) – заряженное тело,
размеры которого малы по сравн-ю с
расст. до других заряж. тел.
Кулон (Франция, 1784 г) на опыте опред-л
силу взаимодействия точечных q.
7

8.

F1
r
+q1
FК
Здесь:
F2
+q2
1
4 0
+q1
q1 q2
r
F1
2
r
F2
-q2
Закон Кулона
Электр.
постоянная.
FK - вектор силы, направлен вдоль
прямой, соед-щей q.

9.

• Обозначим:
Тогда:
q1 q2
FК k
2
r
Закон Кулона
9

10.

• Кулоновские силы велики.
• Так если в человеке е будет на 1%
больше, то на расстоянии 1 шага от
такого же человека возникнет сила
отталкивания, равная весу Земли!
10

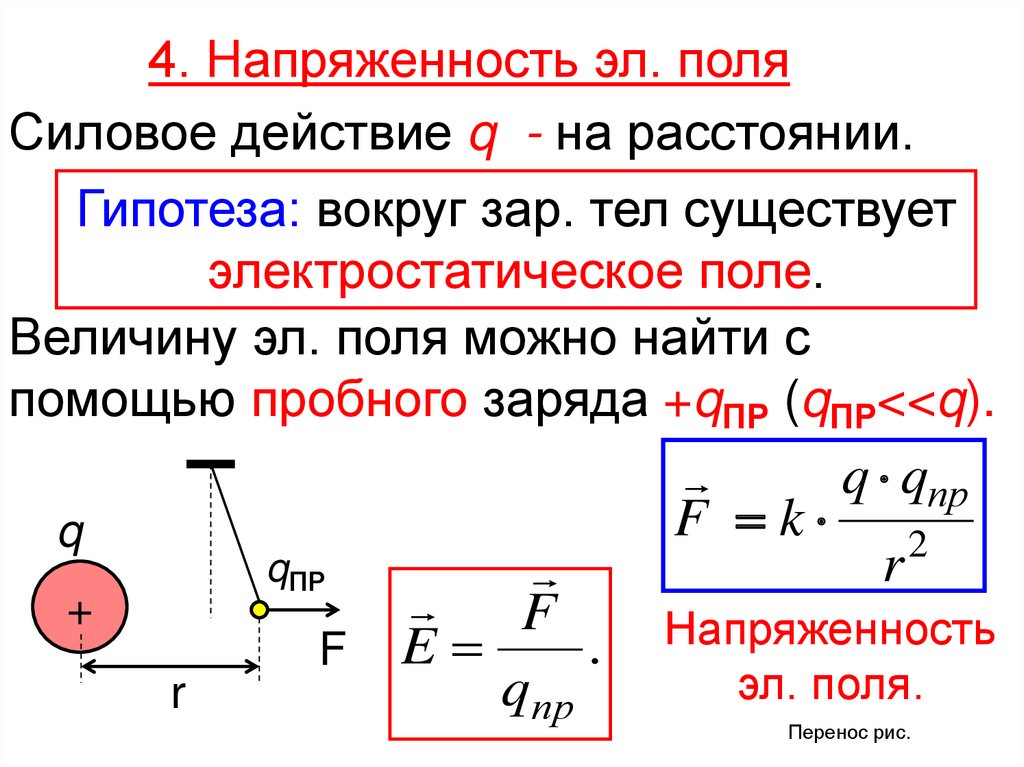
11. 4. Напряженность эл. поля

Силовое действие q - на расстоянии.
Гипотеза: вокруг зар. тел существует
электростатическое поле.
Величину эл. поля можно найти с
помощью пробного заряда +qПР (qПР<<q).
q
F
.
F E
qпр
qПР
+
r
q qпр
F k 2
r
Напряженность
эл. поля.
Перенос рис.

12.

q
+
qПР
F
q qпр
F k 2
r
F
E
.
qпр
Напряженность
эл. поля.
r
Е – силовая характер-ка эл. поля и равна
силе, действ. на ед. полож. q, наход-ся в
этом поле.
Размерность :
Н В
E
Кл м
Если q помещен в эл. поле напряжен. Е, то на
него действует сила:
F qE

13.

E
Если заряд (+),
то направл.
совпадает с F .
Поле E от точеч. заряда q.
На qПР действ. сила:
q
q
пр
F k 2
F
q
r
E
k .
qпр
E
r
q
4 0 r
2
Напряжен. эл. поля
.
2
от точеч. q.

14.

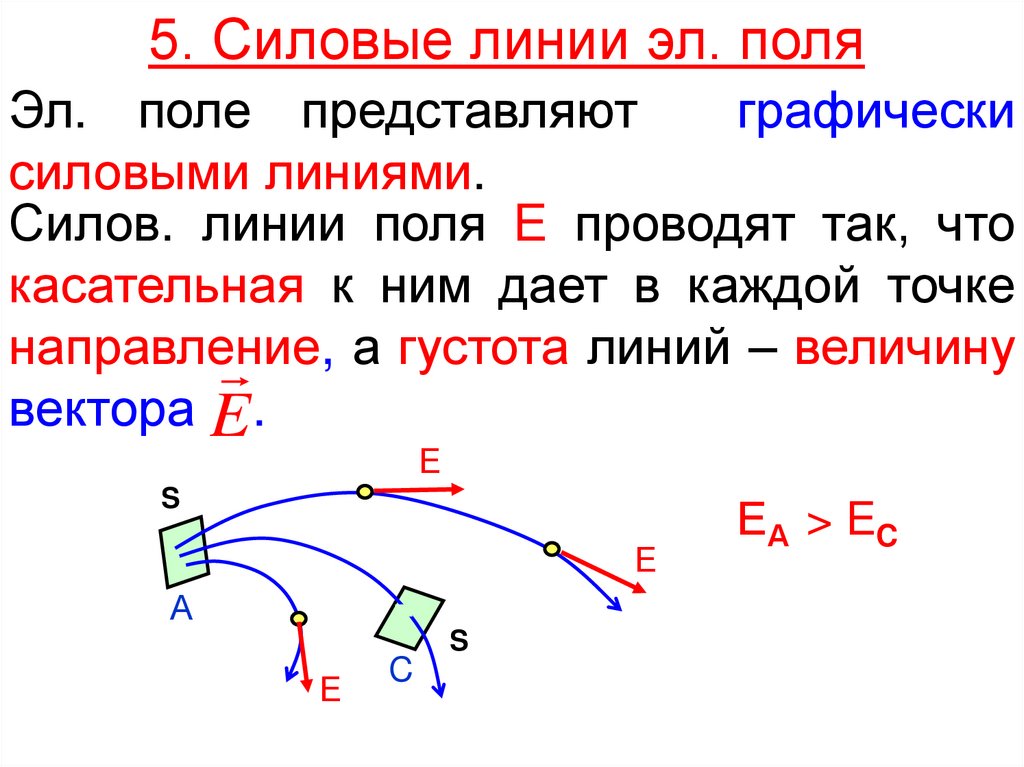
5. Силовые линии эл. поля
Эл. поле представляют
графически
силовыми линиями.
Силов. линии поля Е проводят так, что
касательная к ним дает в каждой точке
направление,
а густота линий – величину
вектора E .
Е
S
Е
А
Е
C
S
ЕА > EC

15.

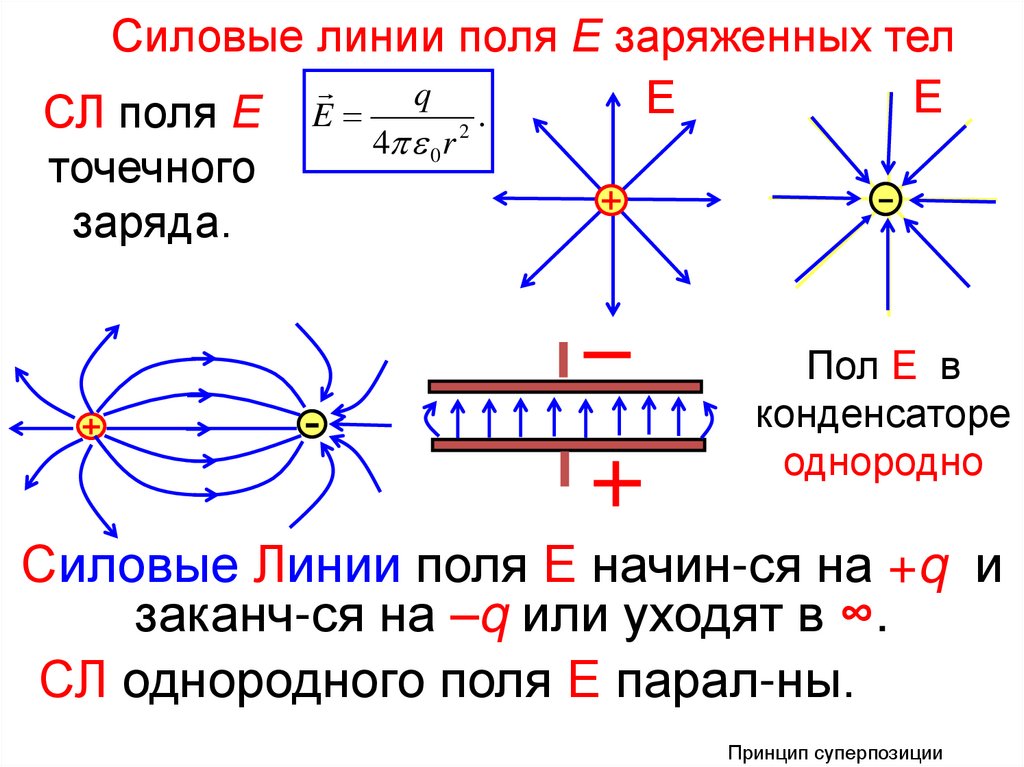
Силовые линии поля Е заряженных тел
q
Е
Е
.
СЛ поля Е E
точечного
заряда.
4 0 r 2
Пол Е в
конденсаторе
однородно
Силовые Линии поля Е начин-ся на +q и
заканч-ся на –q или уходят в ∞.
СЛ однородного поля Е парал-ны.
Принцип суперпозиции

16.

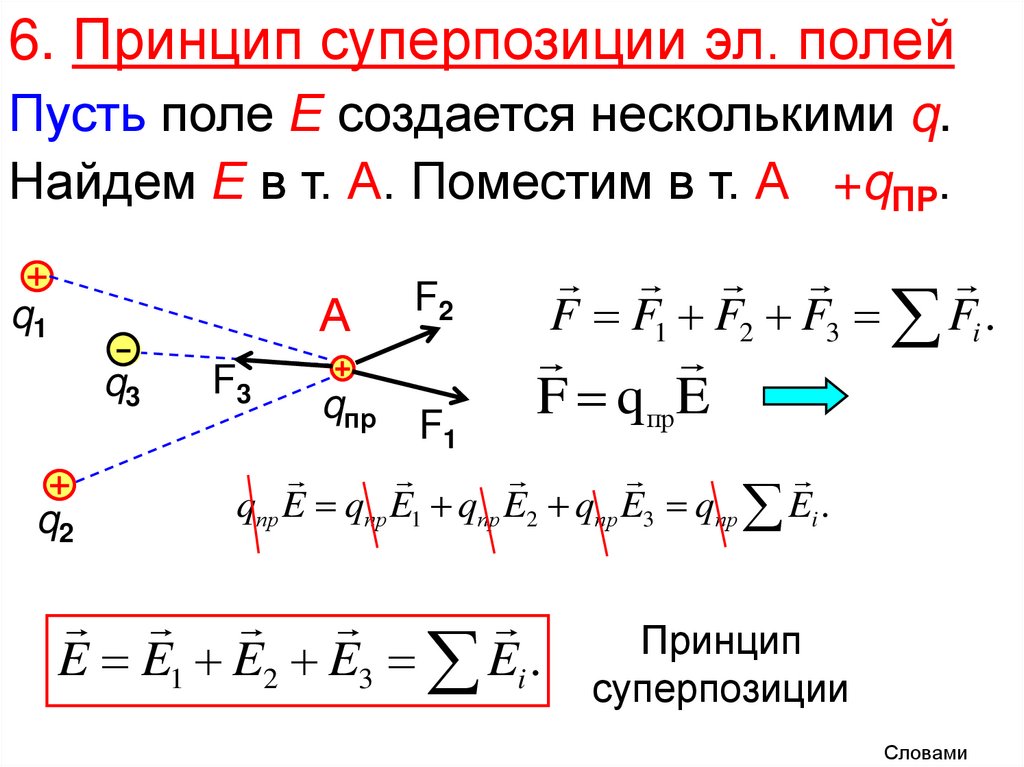
6. Принцип суперпозиции эл. полей
Пусть поле Е создается несколькими q.
Найдем Е в т. А. Поместим в т. А +qПР.
А
q1
q3
q2
F3
qпр
F2
F1
F F1 F2 F3 Fi .
F qпр E
qпр E qпр E1 qпр E2 qпр E3 qпр Ei .
E E1 E2 E3 Ei .
Принцип
суперпозиции
Словами

17.

Напряжен. эл. поля Е от системы
точеч. q равна векторной сумме полей
Еi, создаваемых в данной точке
каждым из q в отдельности.
Принцип суперпоз. позволяет вычислять
поле Е от любой системы q. Если заряд q
протяженный, то его разбивают на малые
части dq и поле от них суммируют
векторно.

18.

7. Потенциал
Электрическое поле Е является потенцным и заряд q в нём обладает потенц.
энергией П.
Если q отпустить, то под действием
+q
FК его П энергия превр-ся в кинет.
FК
Е
-Q
Потенциал.

19.

П
q
Потенциал φ – энергетическая
хар-ка эл. поля, скаляр
Дж В Кл
В
Кл
Кл
(Вольт)
П зар. q в эл. поле с потенц. φ: П=q∙φ
П
Qq
Q
φ поля от точечн. Q:
q 4 0 r q 4 0 r
Q
4 0 r
φ эл. поля от
точечного зар. Q

20.

Потенц. эл. поля от нескольких q:
i
Потенц. эл. поля от системы q
равен алгебраической сумме φi
от каждого из qi.

21.

Электроёмкость и энергия
электростатического поля

22. 1. Электроёмкость проводников

С - это cпособность пр-ка накапливать на
поверхности q.
q
C
C – электроёмкость пров-ка.
Электроём-ть С пр-ка есть отношение
заряда q пр-ка к его потенц. φ.
[С] = Кл/В = [Ф](Фарада)
Это больш. вел-на, поэтому мкФ, нФ, пкФ.
1 Ф – ёмкость шара в воздухе R =9·106 м.
22

23.

С пр-ка опред-ся размерами, формой, ε.
Электроёмкость шара
Потенц. шара в среде с ε:
q
q
4 0 R C
ЭлектроёмC 4 0 R кость шара
2. Конденсаторы
Уединенные пр-ки имеют малую С.
Велика С Конденсаторов (две пластины,
между которыми наход-ся диэл-к (ε)).
23

24.

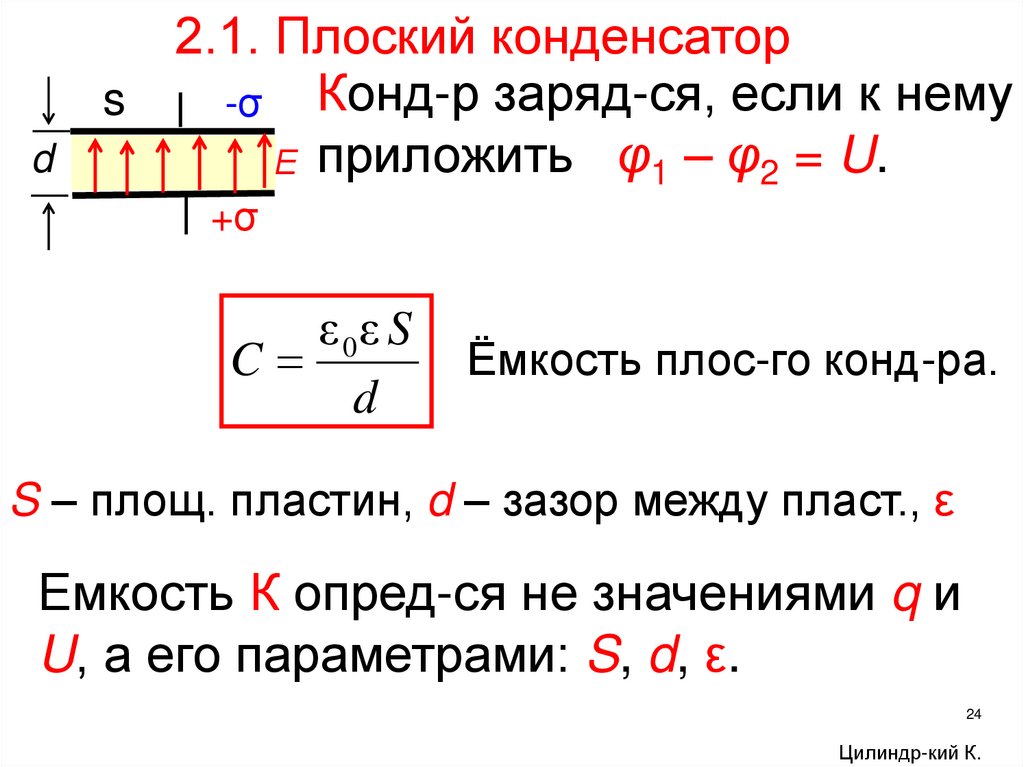
d
2.1. Плоский конденсатор
s
-σ Конд-р заряд-ся, если к нему
Е приложить φ1 – φ2 = U.
+σ
ε 0ε S
C
d
Ёмкость плос-го конд-ра.
S – площ. пластин, d – зазор между пласт., ε
Емкость К опред-ся не значениями q и
U, а его параметрами: S, d, ε.
24
Цилиндр-кий К.

25.

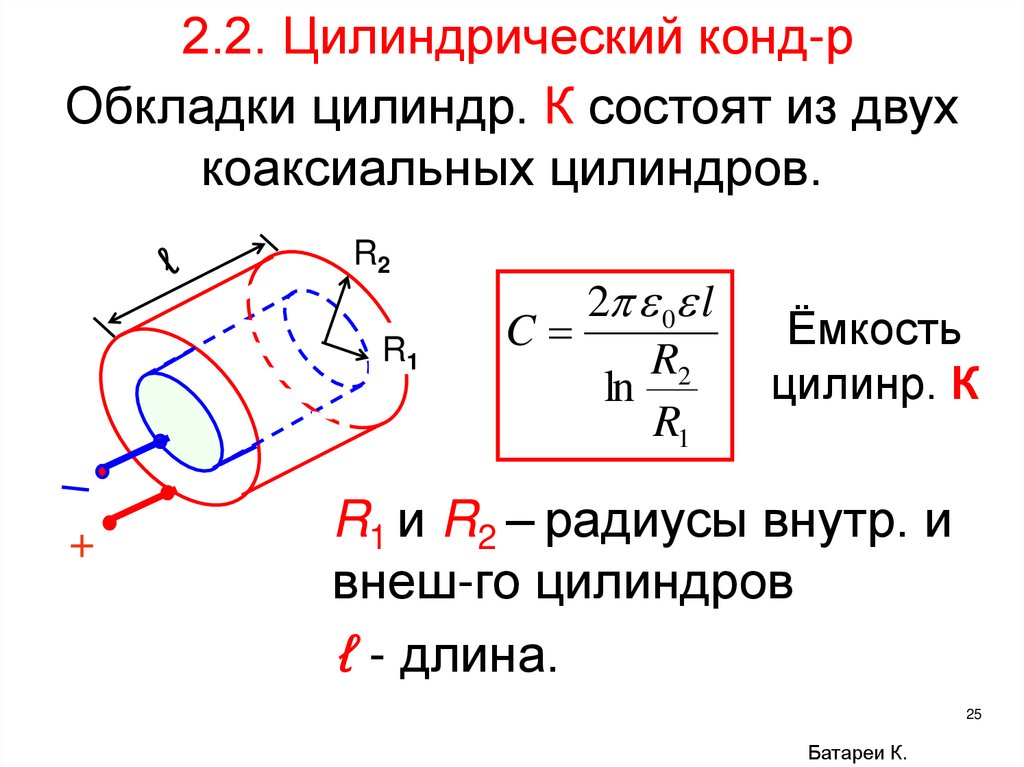
2.2. Цилиндрический конд-р
Обкладки цилиндр. К состоят из двух
коаксиальных цилиндров.
R2
R1
+
2 0 l
C
R2
ln
R1
Ёмкость
цилинр. К
R1 и R2 – радиусы внутр. и
внеш-го цилиндров
ℓ - длина.
25
Батареи К.

26.

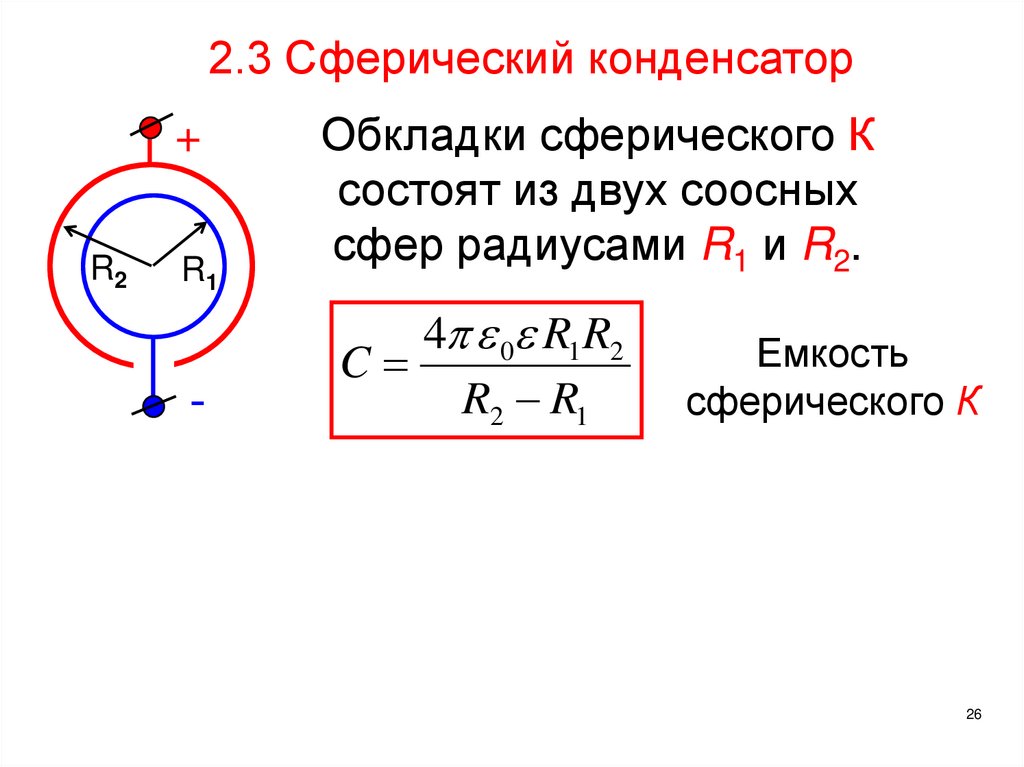
2.3 Сферический конденсатор
+
R2
R1
-
Обкладки сферического К
состоят из двух соосных
сфер радиусами R1 и R2.
4 0 R1 R2
C
R2 R1
Емкость
сферического К
26

27.

3. Параллельное соед-ие конден-ов
q1
С1
q2
С2
Ёмкость батареи К.
q
C
U
Для всех К напряж. U = const.
U
+
q = C·U
q1 = C1U
q2 = C2U
q = q1 +q2
q = UC = U(C1 + C2)
C = C1 + C2 +…+ Cn
Ёмкость С батареи // соединенных
Конденсаторов равна сумме их Сi.
Б. из послед. К

28.

4. Последовательное соед-ние С
С1
С2
U2
U1
U
+
1
1
1
C C 1 C2
1
1
C
Ci
Ёмкость батареи С.
q
C
U
Для всех К заряд q = const
q
U U1 U 2
U
C
q
q
q
q
U1
C1
C C1 C2
q
U2
C2
При вычислении С батареи
послед. соедин-х К суммируются величины, обратные их С
28
Энергия заряж. тел

29.

5. Энергия заряженного пр-ка
Энергия W. Если пр-к имеет q, то его φ=q/C.
Для увелич-я его q, надо перенести на пр-к
dq из ∞, соверш. А:
C
W
2
2
Энергия заряж. пр-ка.

30.

6. Энергия электростат-ого поля
Заряж. Конденсатор тоже имеет W. Пусть
к пластинам К приложено Δφ = U.
s
2
Е
d
+
2
CU
qU q
W
2
2
2C