Электричество. Электростатика. Способы электризации тел

1.

Электричество
ЭЛЕКТРОСТАТИКА
© Парфентьева Наталия Андреевна

2.

ЭЛЕКТРОСТАТИКА
лекция 1

3.

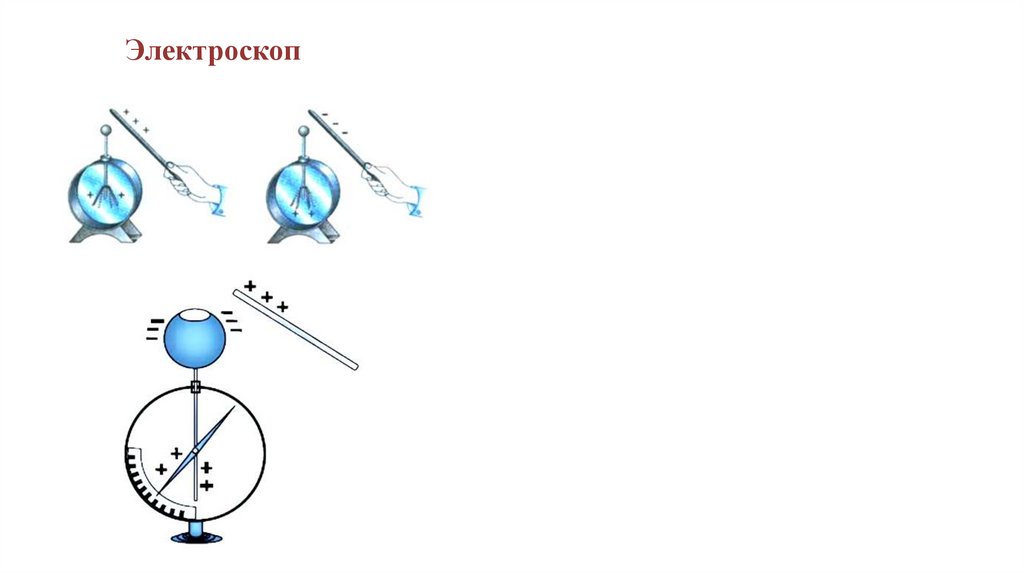
Способы электризации тел
1. Электризация трением (соприкосновением).
2. Электризация через влияние, или метод
электростатической индукции.
3. При освещении металла ультрафиолетовым
источником света.

4.

Электроскоп

5.

Свойства электрических зарядов
1. Существуют заряды только двух видов:
отрицательные и положительные.
qe = – 1,6 10 –19 Кл, а me = 9,1 10 –31 кг
qp = + 1,6 10 –19 Кл, масса mp = 1,67 10 –27 кг.
2. Электрический заряд имеет дискретную природу.
(закон сохранения заряда: q = N qe , где N – целое
число).
3. В изолированной системе, т.е. в системе, тела которой
не обмениваются зарядами с внешними по отношению
к ней телами, алгебраическая сумма зарядов
сохраняется заряда (закон сохранения заряда).

6.

Закон Кулона (1785 г.)
q1 q2
F k
r2
2
1
Н
м
k
9 109
4πε 0
Кл 2
0 8,85 10 12 Ф / м
1 q1 q2
F=
4πε 0 εr 2

7.

Пример. В вершинах квадрата находятся одинаковые по
величине одноименные заряды. Определите величину
заряда q0, который надо поместить в центр квадрата,
чтобы система зарядов находилась в равновесии. Будет
ли это равновесие устойчивым?
F1 F3 F4 F0 0
q2
q2
q q0
F1 F3 k 2 F4 k 2 F0 2k 2
a
2a
a
F1 cos45 F3 cos45 F4 – F0 0
q2
q2
2q q0
k 2 2 k 2 k
0
2
a
2a
a
1 2 2
q q
0,95q
0
4

8.

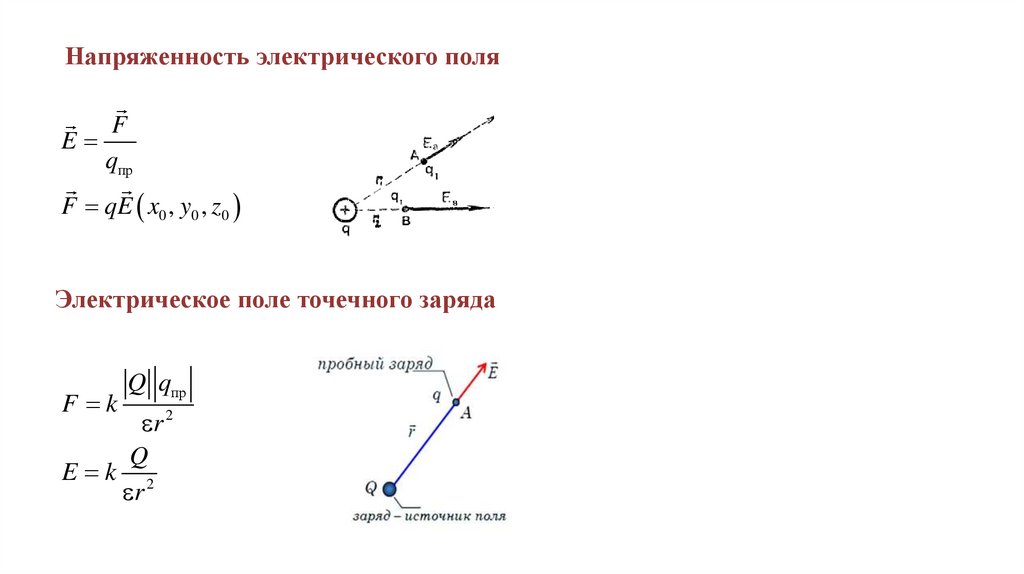
Напряженность электрического поля
F
E
qпр
F qE x0 , y0 , z0
Электрическое поле точечного заряда
F k
Q qпр
r 2
Q
E k 2
r

9.

Графическое изображение электрического поля
Силовая линия – это линия, касательная в каждой точке
которой совпадает с вектором напряженности в этой точке.
Однородное поле
Неоднородное поле
Поле точечного заряда
Поле диполя
Поле двух положительных зарядов

10.

Принцип суперпозиции полей
Если поле создается несколькими зарядами, то
напряженность электрического поля в данной точке
определяется векторной суммой напряженности полей,
создаваемых в этой точке каждым зарядом в отдельности.
Это следствие независимости действия сил: поле каждого
источника действует так, как будто других источников
поля нет (принцип суперпозиции полей):
E = E1 E2 E3 ...

11.

Пример. Напряженность электрического поля,
создаваемого тремя бесконечными параллельными
плоскостями в точках A, B, C, D. Поверхностные
плотности зарядов , 2 и –3 .

12.

Проводники в электрическом поле
Проводники – вещества, в которых есть свободные
электрические заряды.
Напряженность электрического поля внутри
проводника равна нулю.
Силовые линии поля перпендикулярны поверхности
проводника.
Fк = qE
Касательная составляющая вызывает движение
зарядов.

13.

Напряженность электрического поля
заряженной проводящей сферы
Проводящий цилиндр, помещенный
в однородное электрическое поле.

14.

Диэлектрики в электрическом поле
Полярные диэлектрики (H2O, H2S) состоят из диполей
Неполярные диэлектрики (H2O2, N2, CO2), в отсутствии
внешнего поля молекулы не являются диполями, так как
«центры» положительных и отрицательных зарядов совпадают.

15.

Ионные кристаллы, например, NaCl
E = E0 - Eп
E0
ε=
E

16.

Вектор электрической индукции,
электрическое смещение D
D 0ε E
Силовые линии электрического смещения непрерывны

17.

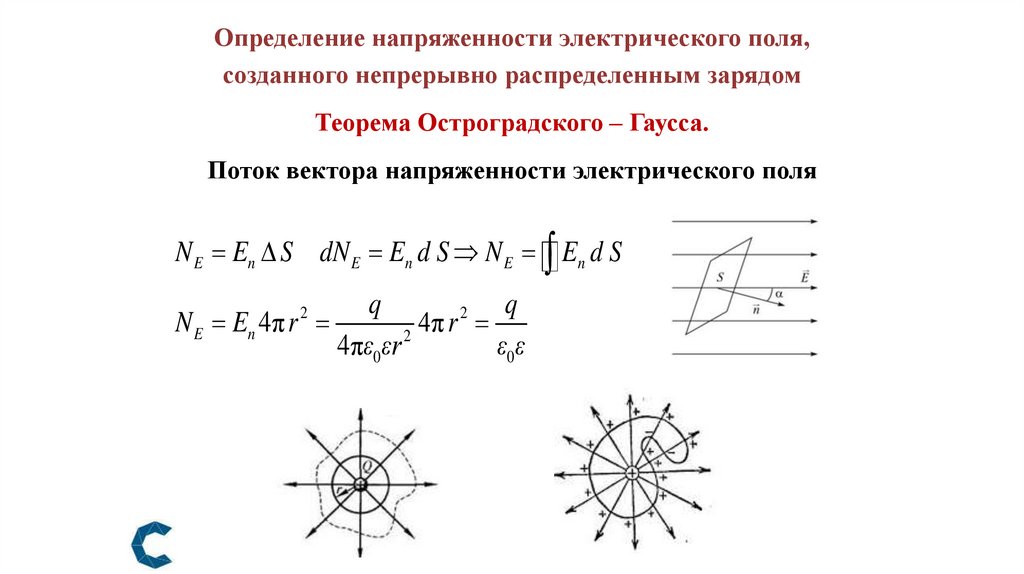
Определение напряженности электрического поля,
созданного непрерывно распределенным зарядом
Теорема Остроградского – Гаусса.
Поток вектора напряженности электрического поля
N E En S dN E En d S N E En d S
q
q
2
N E En 4π r
4π r
2
4πε0εr
ε0 ε
2

18.

N E En d S E1n E2 n ... d S
S
S
q
q q ...
1
E
d
S
E
d
S
...
1n 2n
S
S
2
ε 0ε
i
ε 0ε
1
ρ dV
V
E
dS
n
S
q
ε 0ε
Теорема Остроградского – Гаусса
для вектора электрического смещения.
N D ρq dV
V

19.

Примеры расчета полей
1. Поле, созданное бесконечной равномерно заряженной
плоскостью. – поверхностная плотность заряда, = q/ S.
N E N E бок 2 N E осн
Sосн
2 E Sосн
E
ε 0ε
2ε 0ε
D
2

20.

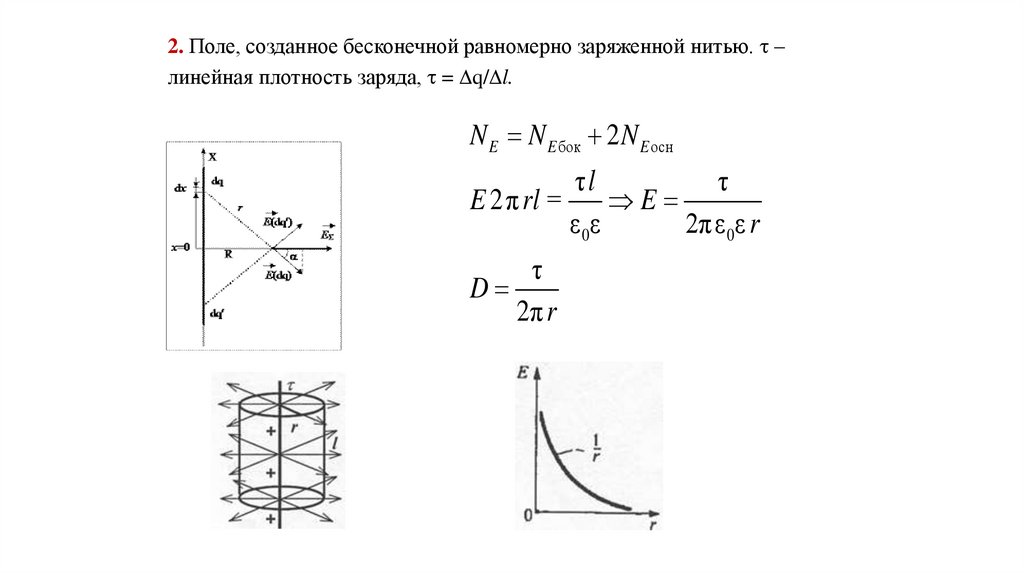
2. Поле, созданное бесконечной равномерно заряженной нитью. –
линейная плотность заряда, = q/ l.
N E N E бок 2 N E осн
τl
τ
E 2 π rl =
E
ε 0ε
2πε 0ε r
τ
D
2π r

21.

3. Поле, созданное бесконечным равномерно заряженным
проводящим цилиндром. – поверхностная плотность
заряда, = q/ S
r <R E=0
r > R N E = N E бок + 2N E осн
σ 2 π Rl
σR
R
E 2 π ε 0ε r l =
E=
E
(ε 1)
ε 0ε
ε 0ε r
ε0 r
D
r

22.

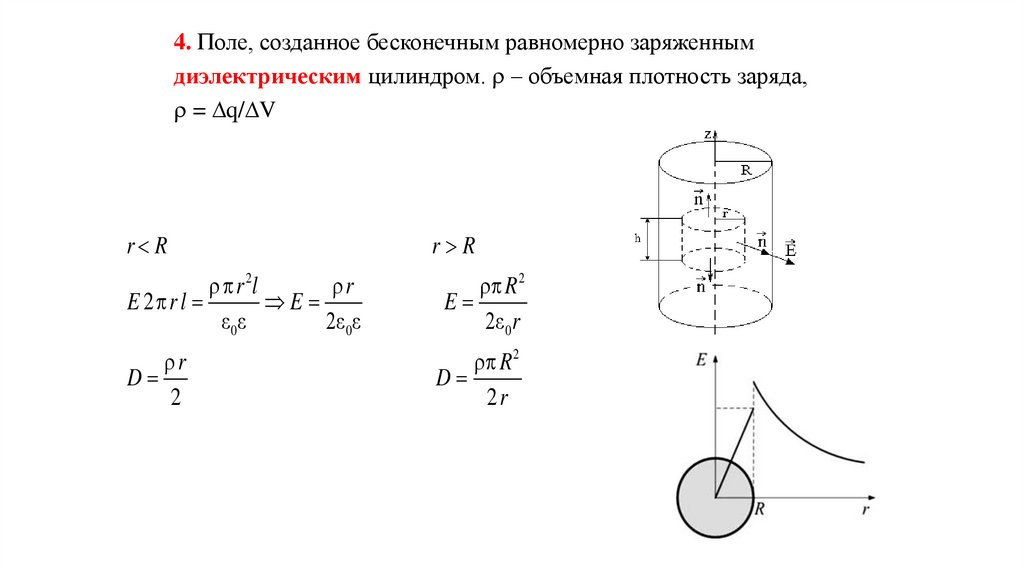
4. Поле, созданное бесконечным равномерно заряженным
диэлектрическим цилиндром. – объемная плотность заряда,
= q/ V
r R
r R
r 2l
r
E 2 r l
E
ε 0ε
2ε 0ε
R 2
E
2ε 0r
r
D
2
R 2
D
2r

23.

5) Поле, созданное проводящей равномерно заряженной
сферой, q – заряд сферы.
E 0 r R
r R
N E E 4πr 2
E 4πr 2
q
q
q
E
E
(ε 1)
2
2
ε 0ε
4πε 0εr
4πε 0r
D
q
4πr 2
6)Поле, созданное равномерно заряженным по объему
шаром. – объемная плотность заряда,
= q/ V
r R
4
π r3
4
2
3
E 4π r
E
r
ε0
3 ε0
4
D r
3

24.

ЭЛЕКТРОСТАТИКА
Лекция 2

25.

Разность потенциалов, потенциал
Работа электростатической силы
по перемещению заряда
F q0 E
1 2 ( траектория I) : AI q0 El12cos q0 Ed
1 1 2 ( траектория II ) : А1 1 q0 Ed , А1 2 0. AII q0 Ed AI
1 – 2 ( траектория III ), Ai F si cos i si cos i di
АIII q0 E si cos i q0 E di q0 Ed
i
i
Работа электростатической силы
по перемещению заряда не зависит от
формы траектории, а зависит от
положения начальной и конечной точек
траектории.

26.

Работа электростатической силы по перемещению заряда
в поле неподвижного точечного заряда Q
F qE
dA F dl Fdl cos Fdr
qQ
dA k 2 dr
r
r2
1 1
qQ
A k 2 dr kqQ
r
r1 r2
r1
qQ
A k 2 dr 0
r
l

27.

Разность потенциалов двух точек поля определяется отношением работы
электростатических сил по перемещению положительного заряда из одной
точки поля в другую к величине этого заряда.
1 1
A1 2
Q
Q
1 2
k k kQ
q
r1
r2
r1 r2
Потенциалом в некоторой точке поля называется отношение работы
электростатической силы по перемещению положительного заряда из данной
точки на бесконечность, к величине этого заряда.
Ar
q
Q
k ( 0 r )
r
1В
1Дж
1Кл
Работа электростатических сил по замкнутому контуру равна нулю.
A k
qQ
dr 0
2
r

28.

Электростатическая сила – консервативная сила.
Электростатическое поле – потенциальное поле.
Работа консервативной силы равна изменению потенциальной
Aконс Wп
энергии, взятой с обратным знаком:
Aконс q 1 2 Wпот1 Wпот2
Wпот
Wпот 0 при r
q0
Потенциал в данной точке поля равен потенциальной
энергии, которой обладает единичный положительный
заряд, помещенный в эту точку поля:
Закон сохранения энергии: Wпот + Wкин = const

29.

Эквипотенциальные поверхности
Геометрическое место точек, имеющих одинаковый потенциал,
называется эквипотенциальной поверхностью.
A
q
q0 4π 0 r
A
φ1 – φ 2
Ed
q0
Силовые линии направлены в сторону уменьшения потенциала и
перпендикулярны эквипотенциальным поверхностям.

30.

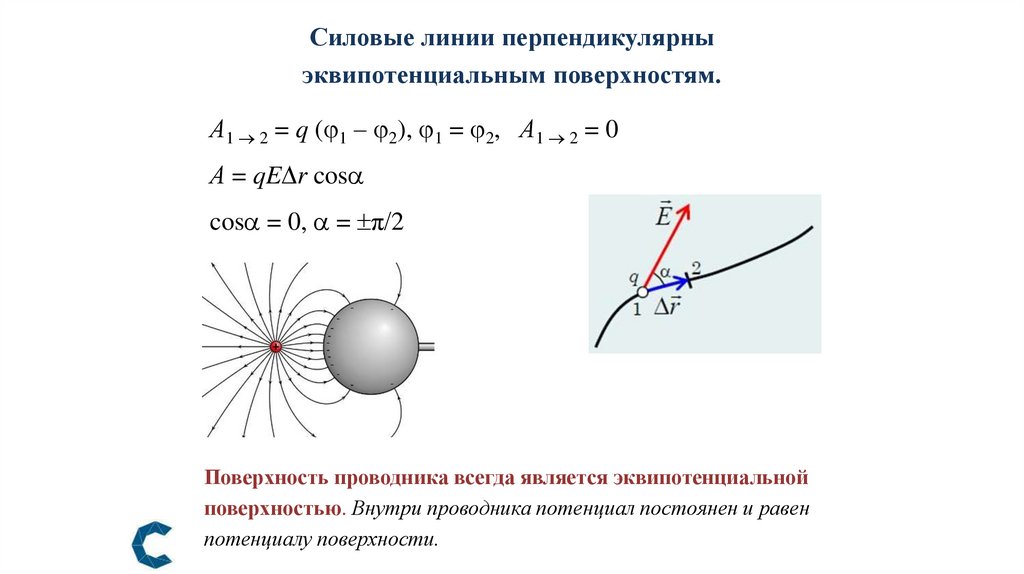
Силовые линии перпендикулярны
эквипотенциальным поверхностям.
А1 2 = q ( 1 – 2), 1 = 2, А1 2 = 0
А = qE r cos
cos = 0, = π/2
Поверхность проводника всегда является эквипотенциальной
поверхностью. Внутри проводника потенциал постоянен и равен
потенциалу поверхности.

31.

Пример. В центре металлической сферической оболочки
с внутренним радиусом R1 и внешним R2 помещают
заряд q. Определите напряженность и потенциал поля
как функции расстояния от центра сферы.
Напряженность поля
E
q
при r R1 и r R2
2
4πε 0 r
Е 0
при R1 r R2
Потенциал поля
При r R1
1 1 1
q
q
q
k k k
kq
r
R1
R2
r R1 R2
q
q
q
1
При R1 r R2 k k k
kq
r
r
R2
R2
q
q
q
q
При r R2 k k k k
r
r
r
r

32.

Связь напряженности электрического поля
с потенциалом
А qE s cos
А q ( 1 – 2 ) – q
qE s cos – q
– E s cos
E
r
E grad i
j
ki
x
y
z
Градиент характеризует быстроту изменения скалярной
величины в направлении ее наибыстрейшего изменения.

33.

Примеры
1. Определение напряженности поля точечного заряда
q
4π 0 r
d
q
E
dr 4π 0 r 2
U
2. Напряженность поля конденсатора: E
d
3. Неоднородное поле
3i 4 j
Ex
3 В / м E y
4 В/м
x
y
E 5В / м

34.

Принцип суперпозиции для потенциала
φ φ1 φ 2
1 q1 q2
φ=
4πεε 0 r1 r2
Потенциал поля диполя
q 1 1
φ=
4πε 0 ε r1 r2

35.

Электроемкость.
Электроемкость уединенного проводника
Δq CΔφ
Δq
C=
Δφ
q
φ=
С 4πε 0εr
4πε 0εr
1Кл А 2 с 4
С 1Ф
1В кг м 2
Электроемкость проводника численно равна заряду, который
надо сообщить проводнику, чтобы повысить его потенциал на
единицу (на 1 В).

36.

Электроемкость конденсатора
q
C
1 2
σ
σ
σ
E
2ε 0 ε 2ε 0ε ε 0ε
σd
qd
Δφ = Ed =
=
ε 0 ε ε 0 εS
ε 0 εS
C
d

37.

Последовательное и параллельное
соединение конденсаторов
1 – 2 ( 1 – А ) ( А – B ) ( B – 2 )
q
q
q
q
Cэкв C1 C2 C3
1
1
1
1
Cэкв C1 C2 C3
1
1
Cэкв
i Ci

38.

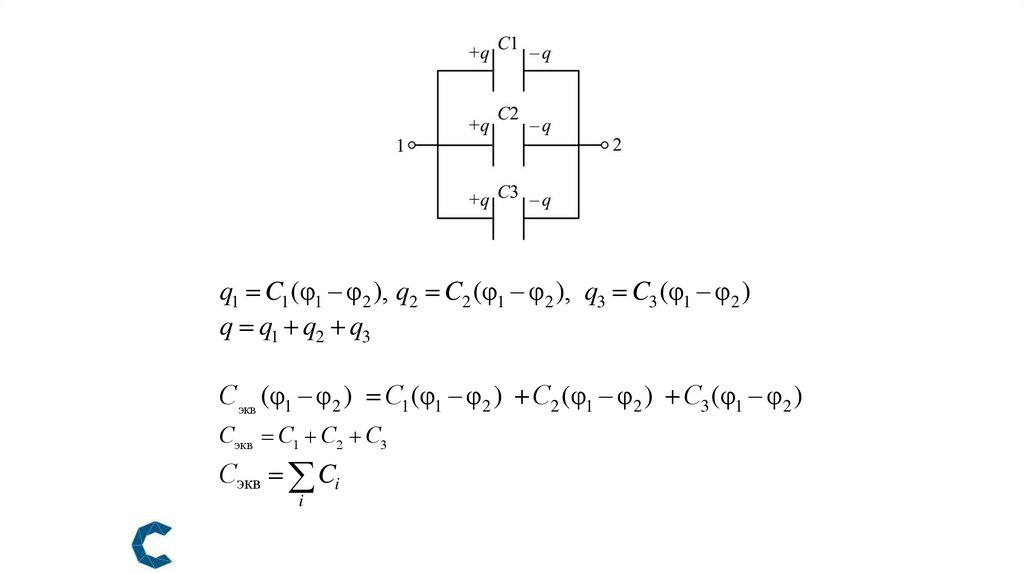
q1 C1 (φ1 – φ2 ), q2 C2 (φ1 – φ2 ), q3 C3 (φ1 – φ 2 )
q q1 q2 q3
Сэкв (φ1 – φ2 ) C1 (φ1 – φ2 ) C2 (φ1 – φ2 ) C3 (φ1 – φ 2 )
Сэкв С1 С2 С3
Сэкв Ci
i

39.

Энергия электрического поля
1. Плоский конденсатор.
E=
q
σ
σ=
S
2ε 0ε
Fэ = qE =
qσ
2ε 0ε
Работа ,совершаемая внешней силой
qσ
Δd d d 2 – d1
А = FΔd =
2ε 0ε
C1
ε εS
ε 0 εS
C2 0
d2
d1
q2
q2
q 2d1
q 2d 2
q q
(d 2 – d1 )
A
2ε 0εS 2ε 0εS 2C2 2C1
2ε 0εS

40.

Работа внешней силы равна работе электростатической
силы, взятой с обратным знаком A Аэ .
q2
q2
Изменение энергии электрического поля Wэ – Аэ
2C1 2C2
q2
q2
q 2 CU 2
Wэ2 – Wэ1
Wэ
2C2 2C1
2C
2
ε 0 εS
d
CU 2 ε 0εSE 2 d 2 ε 0εE 2
ε 0 εE 2
Wэ
Sd
V
2
2d
2
2
Плотность энергии электрического поля
U Ed C
Wэ ε 0εE 2 ED
w
.
V
2
2

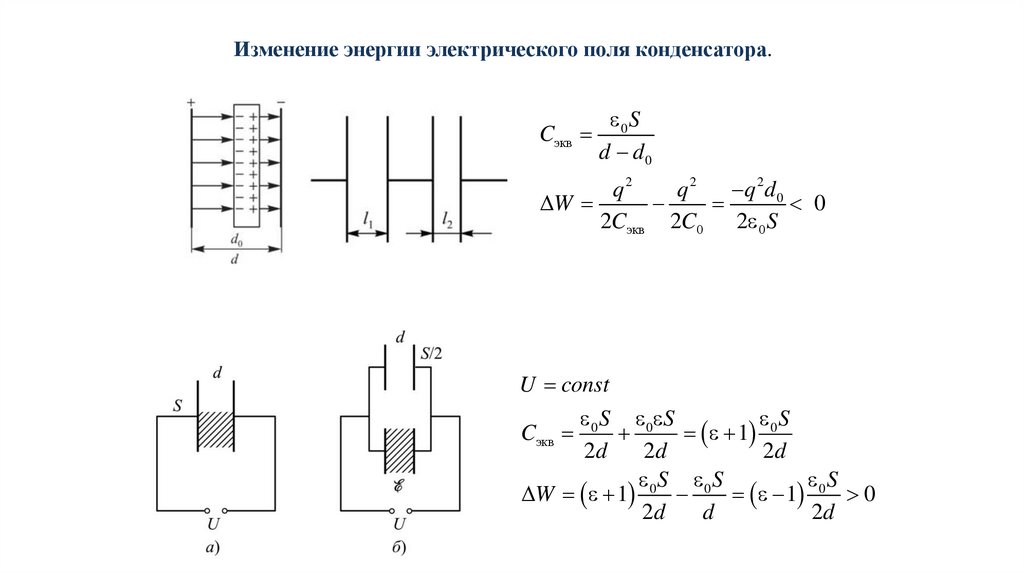
41.

Изменение энергии электрического поля конденсатора.
Cэкв
0 S
d d0
q2
q2
q 2d 0
W
0
2Cэкв 2C0 2 0 S
U const
0 S 0 S
0 S
Cэкв
1
2d
2d
2d
S S
S
W 1 0 0 1 0 0
2d
d
2d

42.

2. Энергия системы проводников.
q
qi i
Wэ
Wэ
2
2
i
Энергия электрического поля двух зарядов
q1q2
q1q2
q1q2
Wэ k
k
k
2r
2r
r
Пример
q
q
2 2 2 1
Wэ 2q 2k k
2kq
a 2
a 2
a
2
2
2
1
2
2
1
m
v
2kq 2
2kq 2
4
2
a 2
2a 2