Similar presentations:
Решение логарифмических неравенств
1.
«Решение простейшихлогарифмических неравенств»
2.
Y=2^y
12
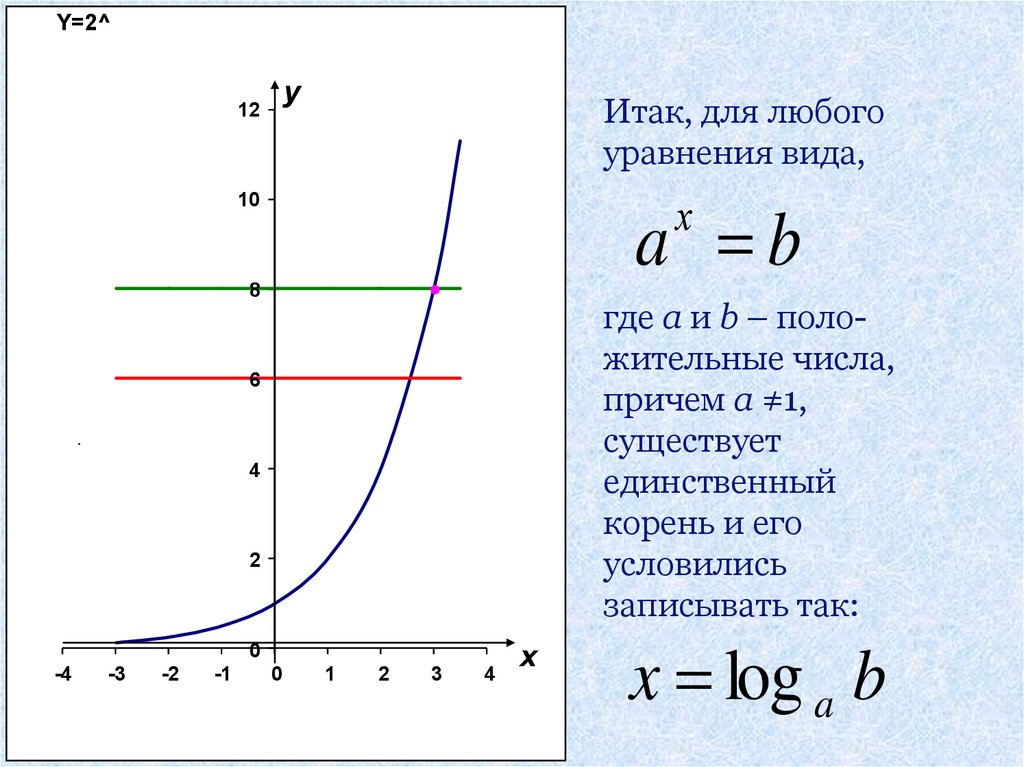
Итак, для любого
уравнения вида,
a b
10
х
8
где а и b – положительные числа,
причем а ≠1,
существует
единственный
корень и его
условились
записывать так:
6
.
4
2
0
-4
-3
-2
-1
0
1
2
3
4
x
x log a b
3. Определение логарифма на языке символов:
1.2.
a
loga b
b
log a b p :
a 0, a 1;
b 0;
a p b.
4.
1. Решите неравенство:log 3 (1 2 x) 2
Решение:
1 2 x 9
x 4
2 x 8
2
log 3 (1 2 x) log 3 3 1 2 x 0
1
2 x 1
3 1
x 2.
Ответ:
1
( 4; )
2
5.
2. Решите неравенство:log 2 (3x 2) log 2 (6 5x)
Решение:
x 1
3x 2 6 5 x 8 x 8
log 2 (3x 2) log 2 (6 5 x)
1
6 5 x 0
6 5 x x
2
Ответ:
1
(1; ).
2
6.
3. Решите неравенство:x 2 lg x 1000
Решение:
Прологарифмируем обе части неравенства по
основанию 10.
lg x 2 lg x lg 1000
;
( 2 lg x) lg x 3 ;
lg 2 x 2 lg x 3 0;
Ответ:
0,1;1000
7. 4.
Необходимо решить неравенство:Изобразим на числовой прямой полученное решение
Ответ :
8.
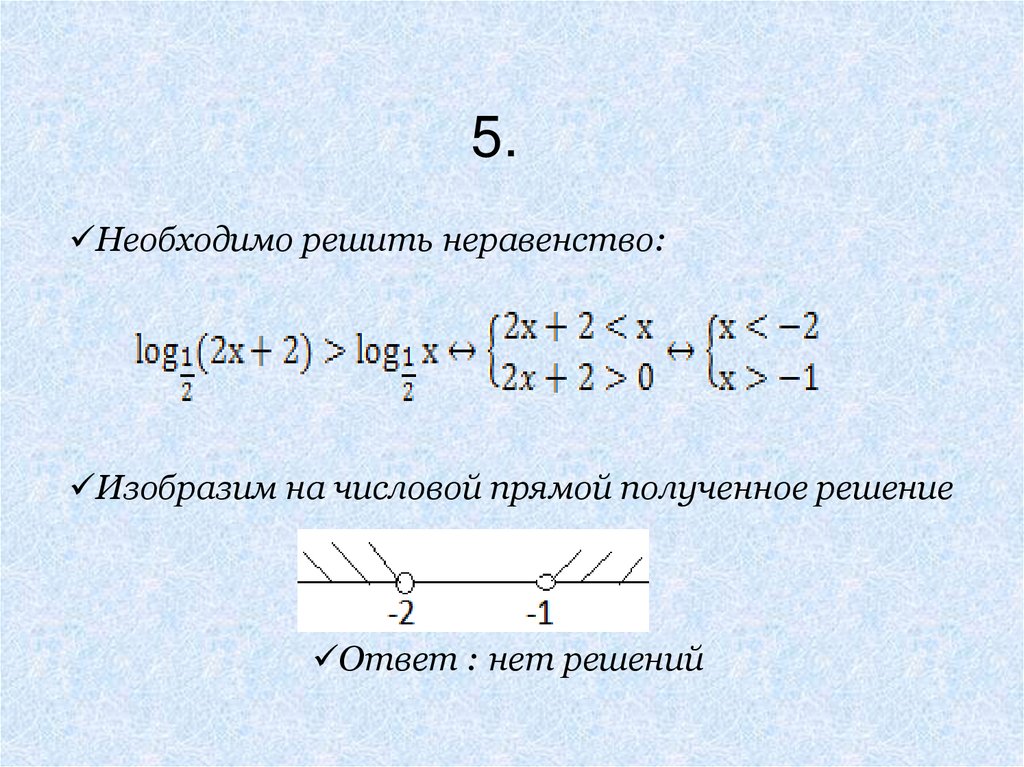
5.Необходимо решить неравенство:
Изобразим на числовой прямой полученное решение
Ответ : нет решений
9. Домашнее задание
1. Законспектировать материалпрезентации с примерами решения.
2. Фото конспектов в тетради прислать в
обсуждение «Математика».
3. Посмотреть видеофрагмент по теме
(конспектировать не нужно).
4. Повторить материал по учебнику:
Колмогоров А.Н. Алгебра 10-11. Параграф
10, пункт 39 (страницы 233-234).







 mathematics
mathematics








