Четыре замечательные точки треугольника

1. Четыре замечательные точки треугольника

2.

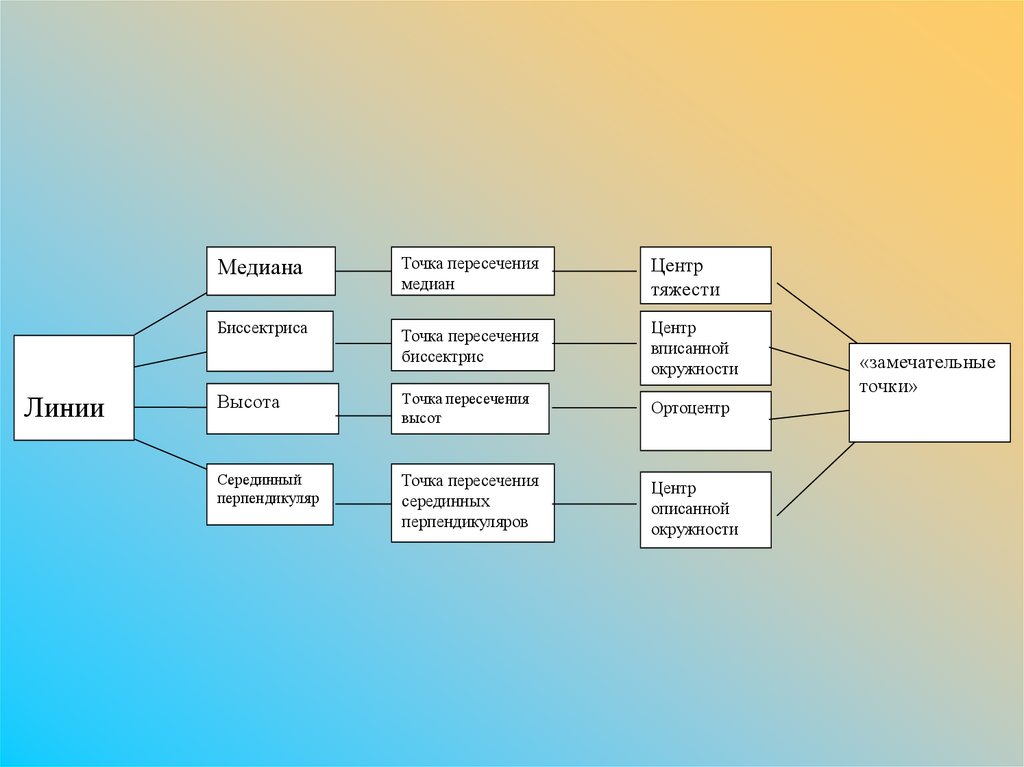
Линии
Медиана
Точка пересечения
медиан
Центр
тяжести
Биссектриса
Точка пересечения
биссектрис
Центр
вписанной
окружности
Высота
Точка пересечения
высот
Ортоцентр
Серединный
перпендикуляр
Точка пересечения
серединных
перпендикуляров
Центр
описанной
окружности
«замечательные
точки»

3.

Точка пересечения медиан
треугольника
Точка пересечения
биссектрис треугольника
Точка пересечения высот
треугольника
Точка пересечения
серединных
перпендикуляров
треугольника

4.

5.

Медианой треугольника
называется отрезок,
соединяющий любую вершину
треугольника с серединой
противоположной стороны.
Любой треугольник имеет три
медианы.

6.

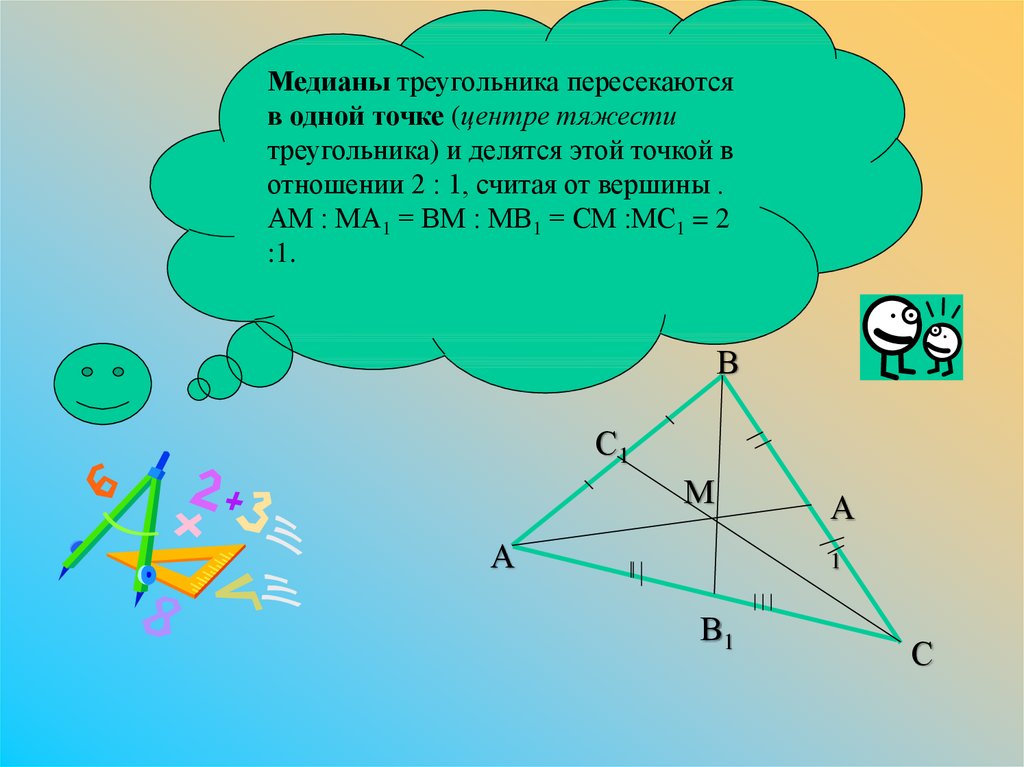
Медианы треугольника пересекаются
в одной точке (центре тяжести
треугольника) и делятся этой точкой в
отношении 2 : 1, считая от вершины .
АМ : МА1 = ВМ : МВ1 = СМ :МС1 = 2
:1.
В
С1
М
А
А
1
В1
С

7.

8.

Биссектрисой называется отрезок
биссектрисы любого угла от вершины до
пересечения с противоположной
стороной. Любой треугольник имеет три
биссектрисы.

9.

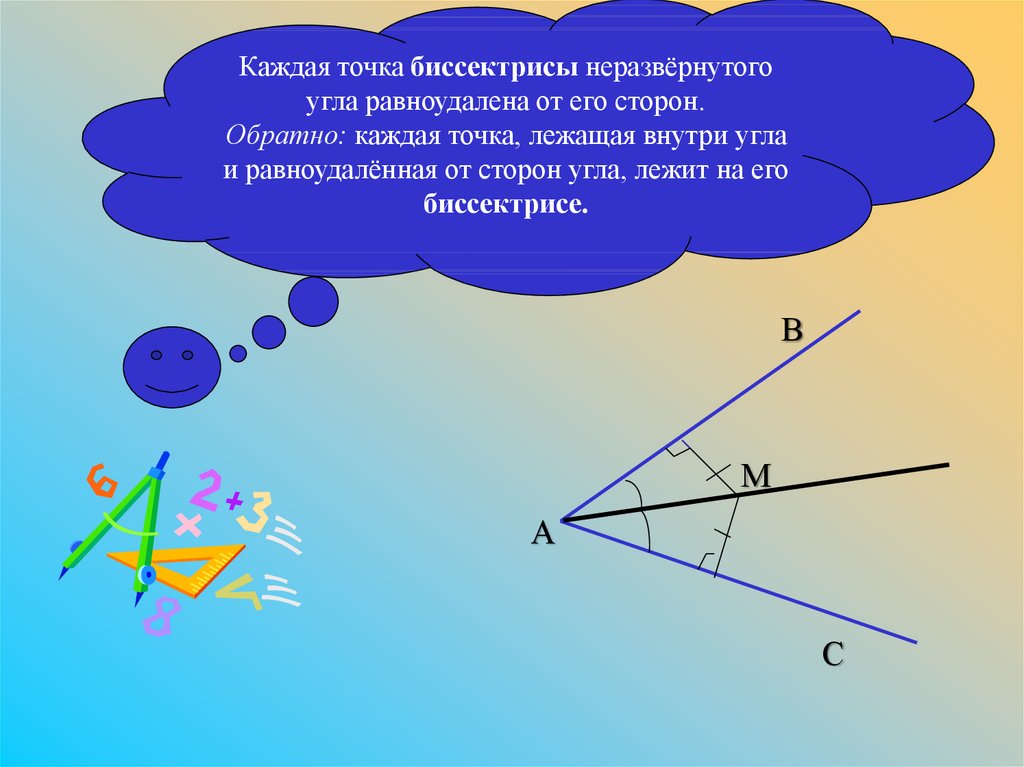
Каждая точка биссектрисы неразвёрнутого
угла равноудалена от его сторон.
Обратно: каждая точка, лежащая внутри угла
и равноудалённая от сторон угла, лежит на его
биссектрисе.
В
М
А
С

10.

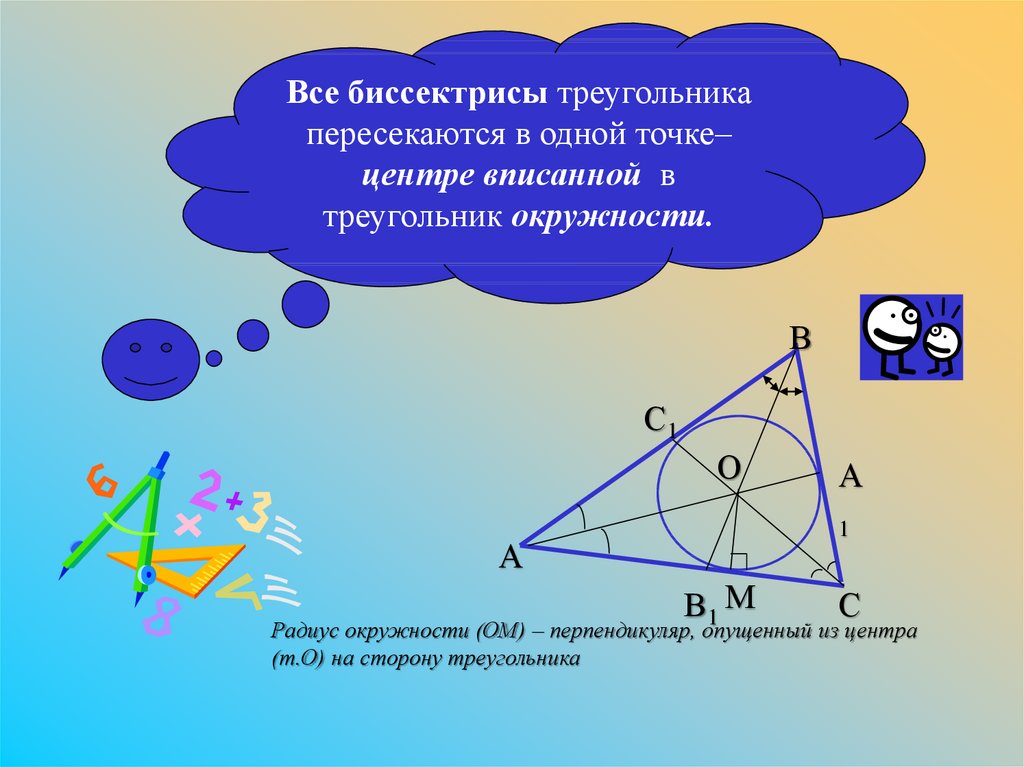
Все биссектрисы треугольника
пересекаются в одной точке–
центре вписанной в
треугольник окружности.
В
С1
О
А
1
А
В1 М
С
Радиус окружности (ОМ) – перпендикуляр, опущенный из центра
(т.О) на сторону треугольника

11.

12.

Высотой треугольника называется
перпендикуляр, опущенный из любой
вершины треугольника на
противолежащую сторону или на ее
продолжение. Любой треугольник
имеет три высоты

13.

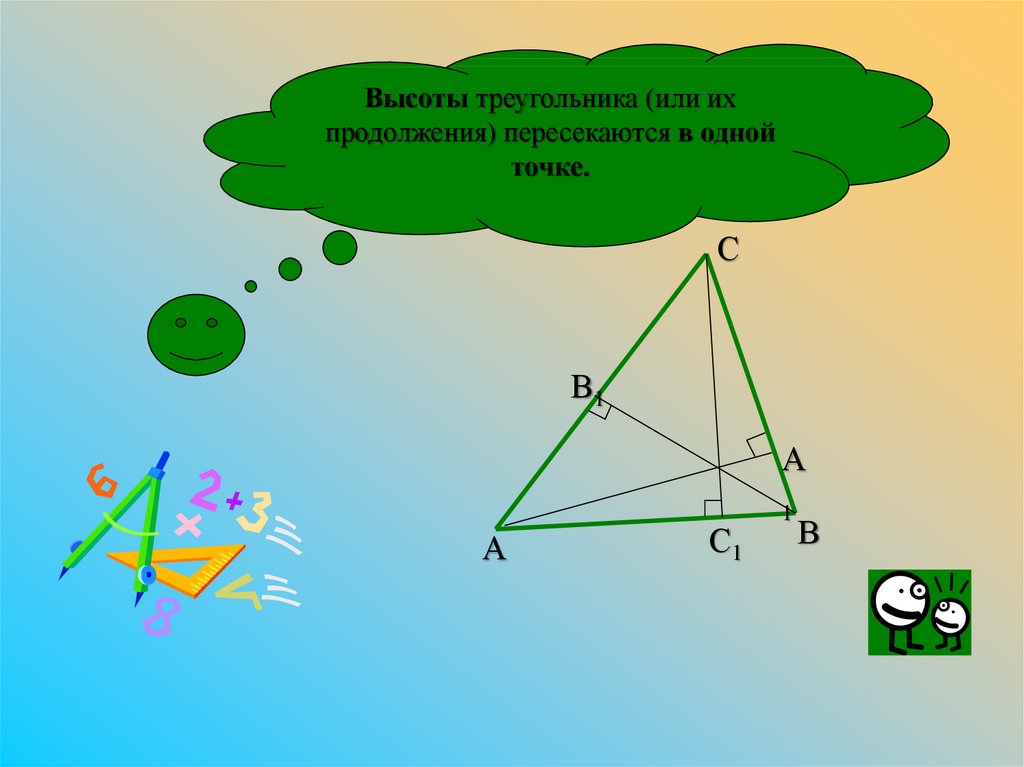
Высоты треугольника (или их
продолжения) пересекаются в одной
точке.
С
В1
А
А
С1
1
В

14.

СЕРЕДИННЫЙ
ПЕРПЕНДИКУЛЯР
C
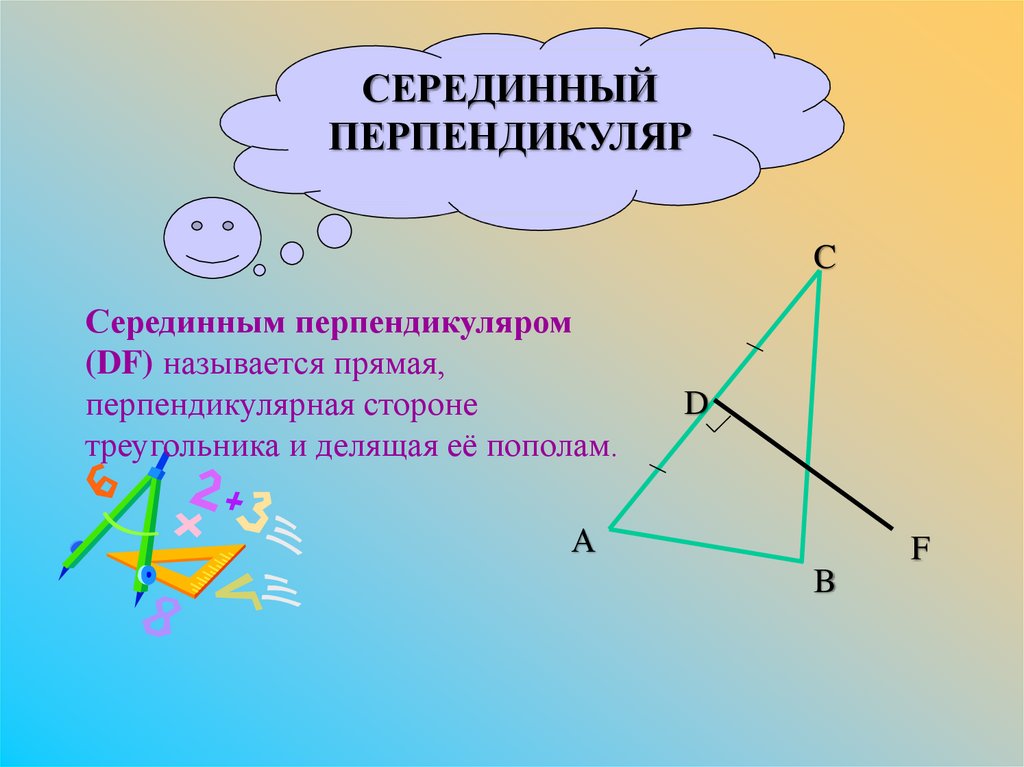
Серединным перпендикуляром
(DF) называется прямая,
перпендикулярная стороне
треугольника и делящая её пополам.
D
А
F
B

15.

16. Серединный перпендикуляр

Серединным перпендикуляром к отрезку
называется прямая, проходящая через
середину данного отрезка и
перпендикулярно к нему. Любой
треугольник имеет три серединных
перпендикуляра

17.

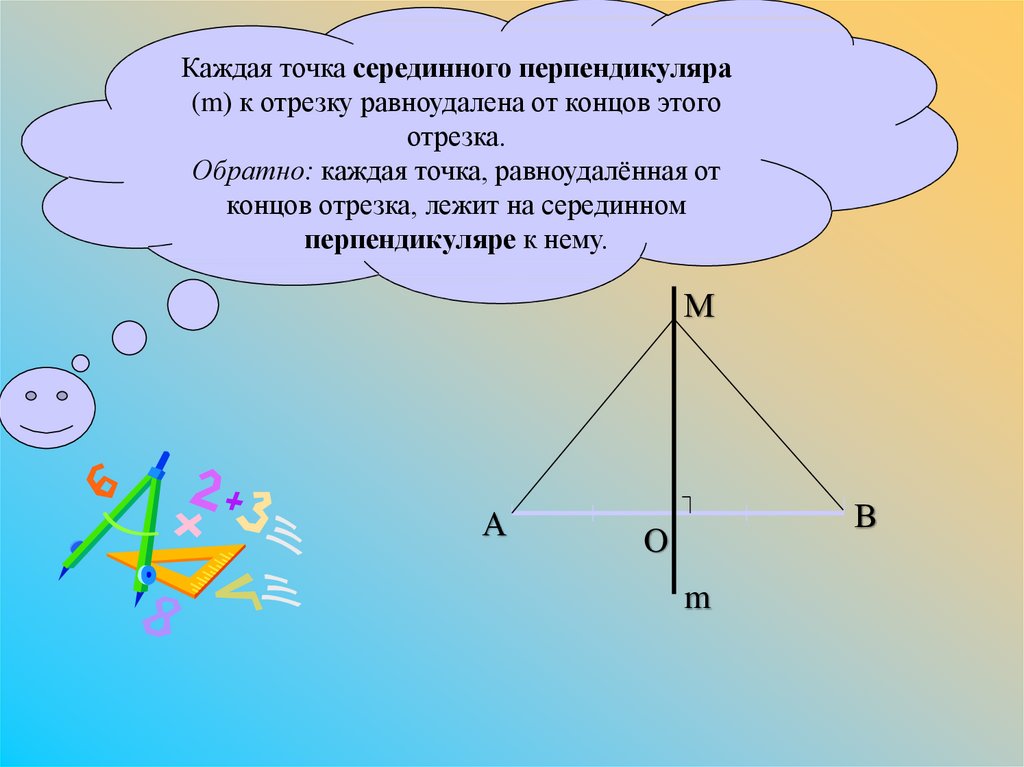
Каждая точка серединного перпендикуляра
(m) к отрезку равноудалена от концов этого
отрезка.
Обратно: каждая точка, равноудалённая от
концов отрезка, лежит на серединном
перпендикуляре к нему.
М
А
В
O
m

18.

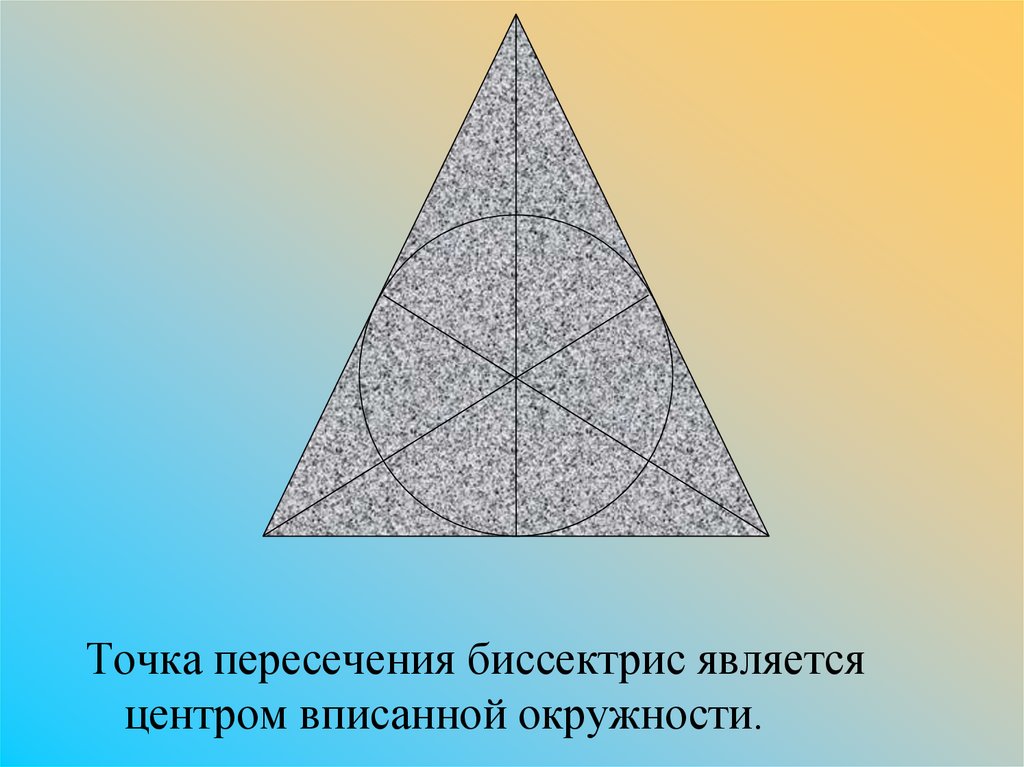
Точка пересечения биссектрис является
центром вписанной окружности.

19.

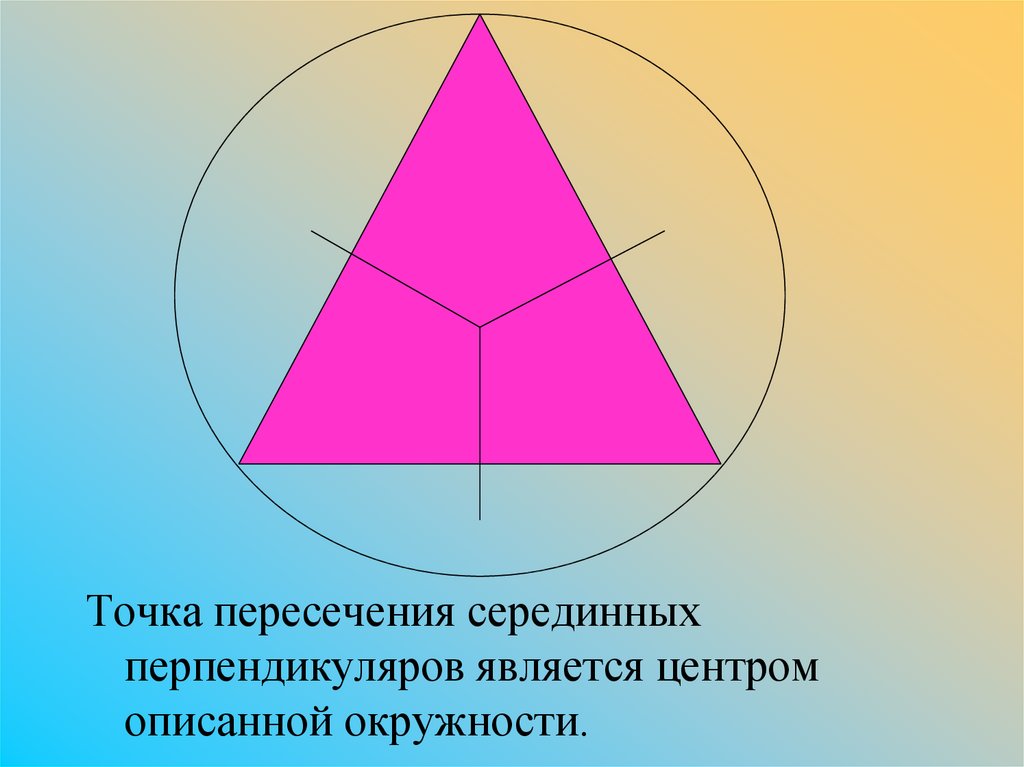
Точка пересечения серединных
перпендикуляров является центром
описанной окружности.

20.

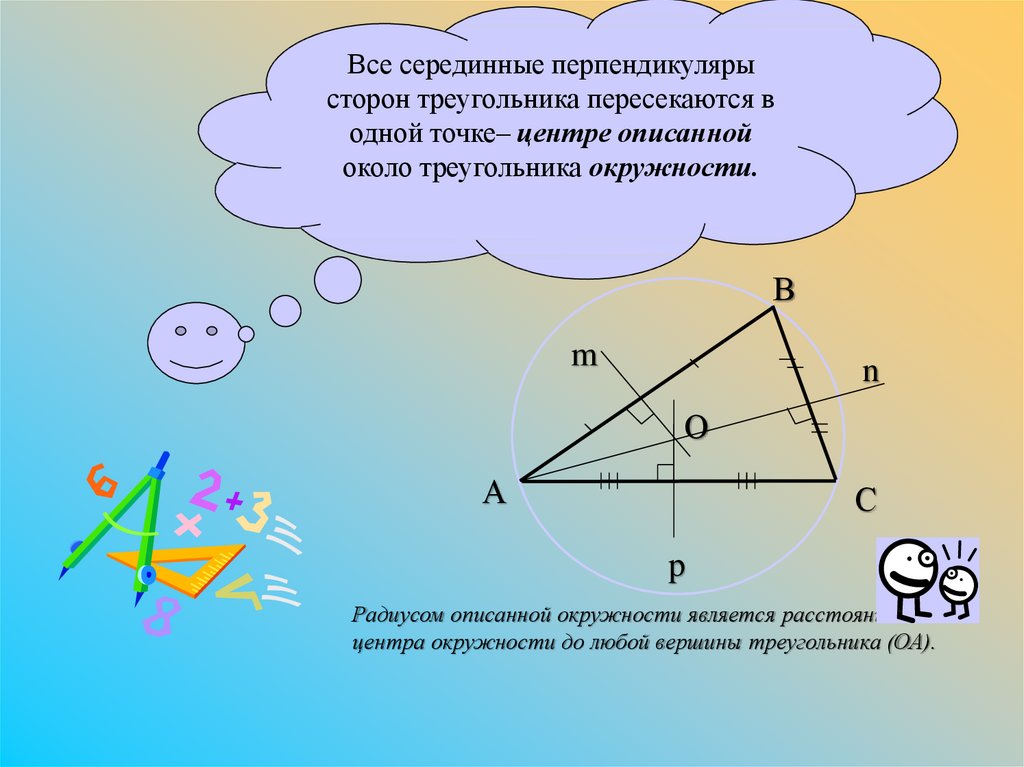
Все серединные перпендикуляры
сторон треугольника пересекаются в
одной точке– центре описанной
около треугольника окружности.
В
m
n
О
А
С
p
Радиусом описанной окружности является расстояние от
центра окружности до любой вершины треугольника (ОА).

21.

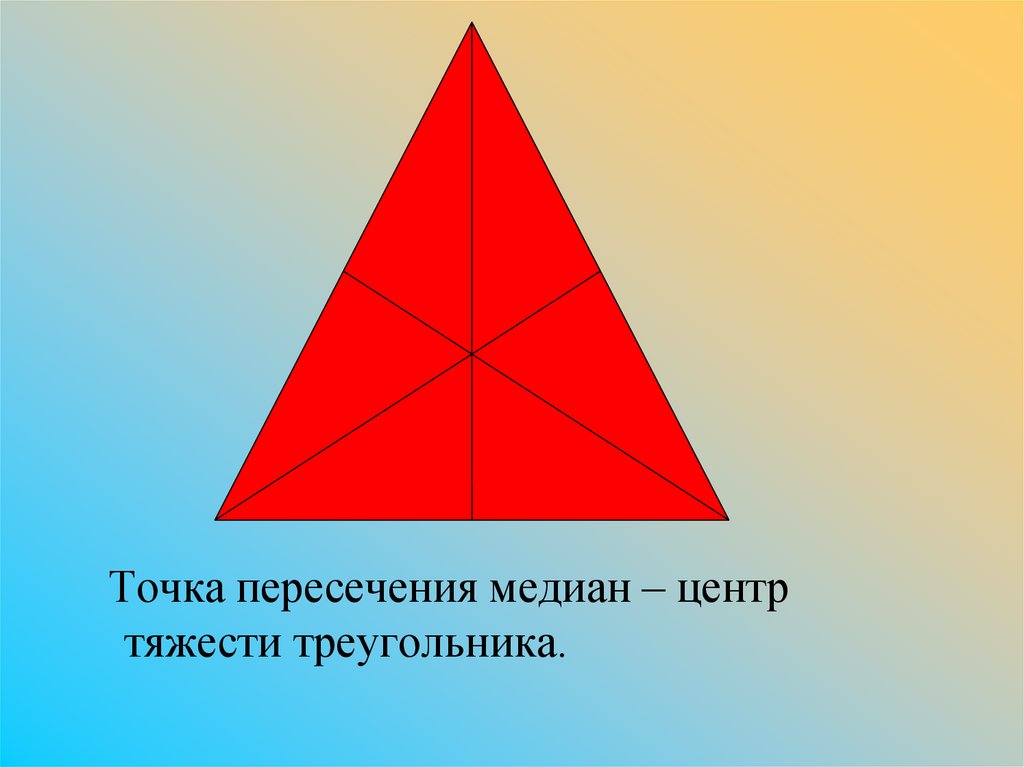
Точка пересечения медиан – центр
тяжести треугольника.

22.

Точка пересечения высот – ортоцентр.