Четыре замечательные точки треугольника

1.

2.

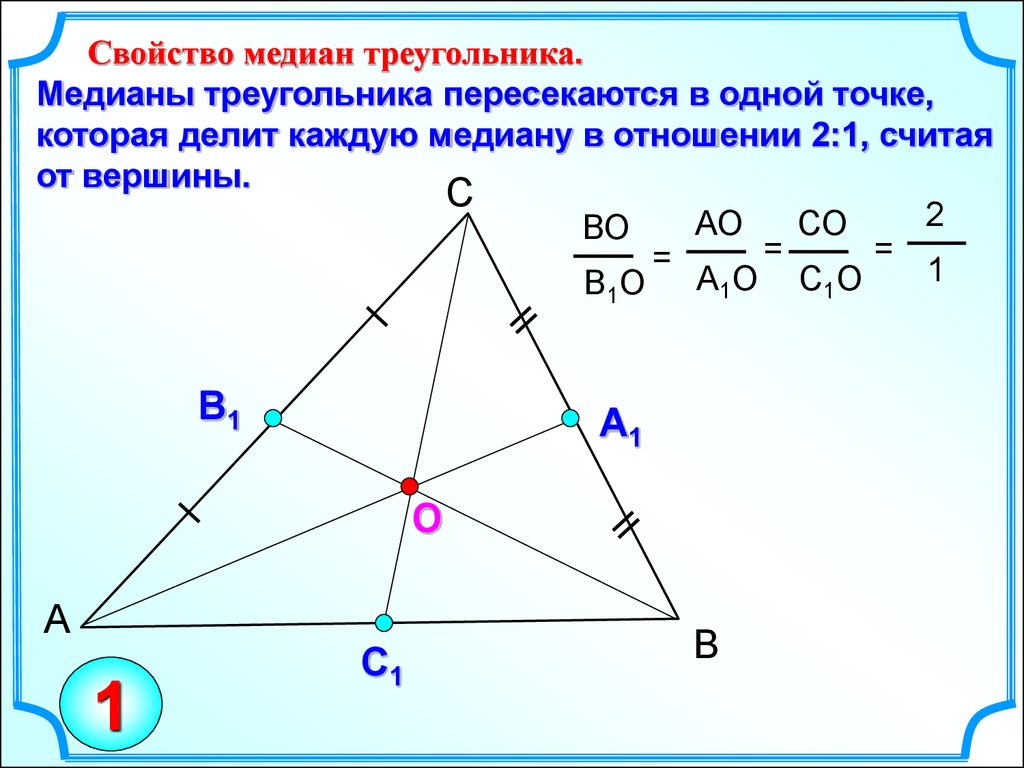
Свойство медиан треугольника.
Медианы треугольника пересекаются в одной точке,
которая делит каждую медиану в отношении 2:1, считая
от вершины.
С
2
АО
СО
ВО
=
=
=
1
В О А1О С1О
1
В1
А1
О
А
1
С1
В

3.

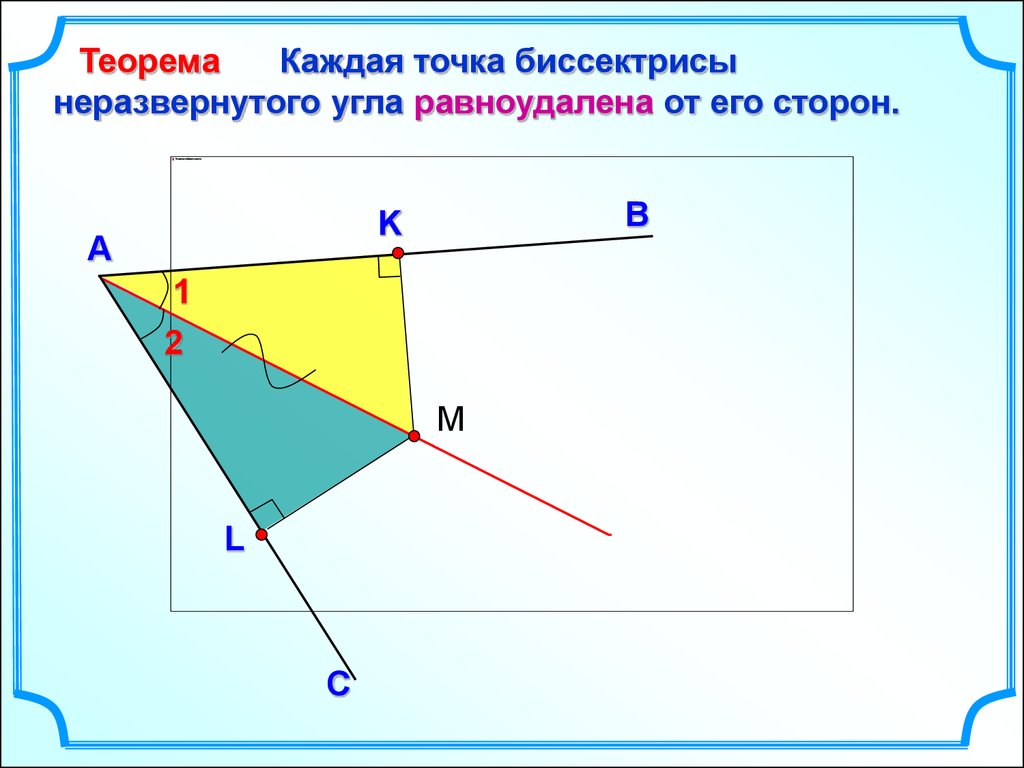
Теорема
Каждая точка биссектрисы
неразвернутого угла равноудалена от его сторон.
В
K
А
1
2
М
L
С

4.

Обратная теорема Каждая точка, лежащая
внутри угла и равноудаленная от сторон угла, лежит
на его биссектрисе.
В
K
А
М
L
С

5.

Следствие
Биссектрисы треугольника пересекаются в одной точке.
В
K С1
А
По теореме
о биссектрисе
угла
ОМ=ОК
ОМ
ОК =ОL
ОL
О
В1
А1
М
L
=
2
С
По обратной теореме т. О
лежит на биссектрисе угла С

6.

Определение
Серединным перпендикуляром к
отрезку называется прямая, проходящая через
середину данного отрезка и перпендикулярно к нему.
М
С
В
a
Прямая a
– серединный перпендикуляр к отрезку.

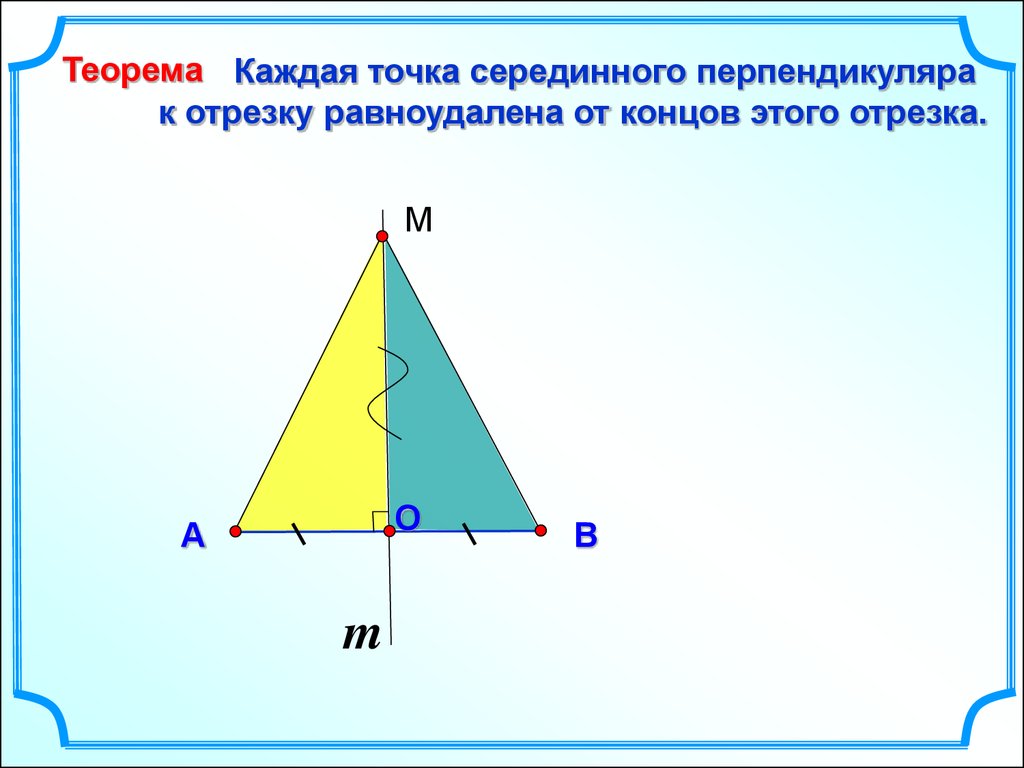
7.

Теорема Каждая точка серединного перпендикуляра
к отрезку равноудалена от концов этого отрезка.
М
O
A
m
B

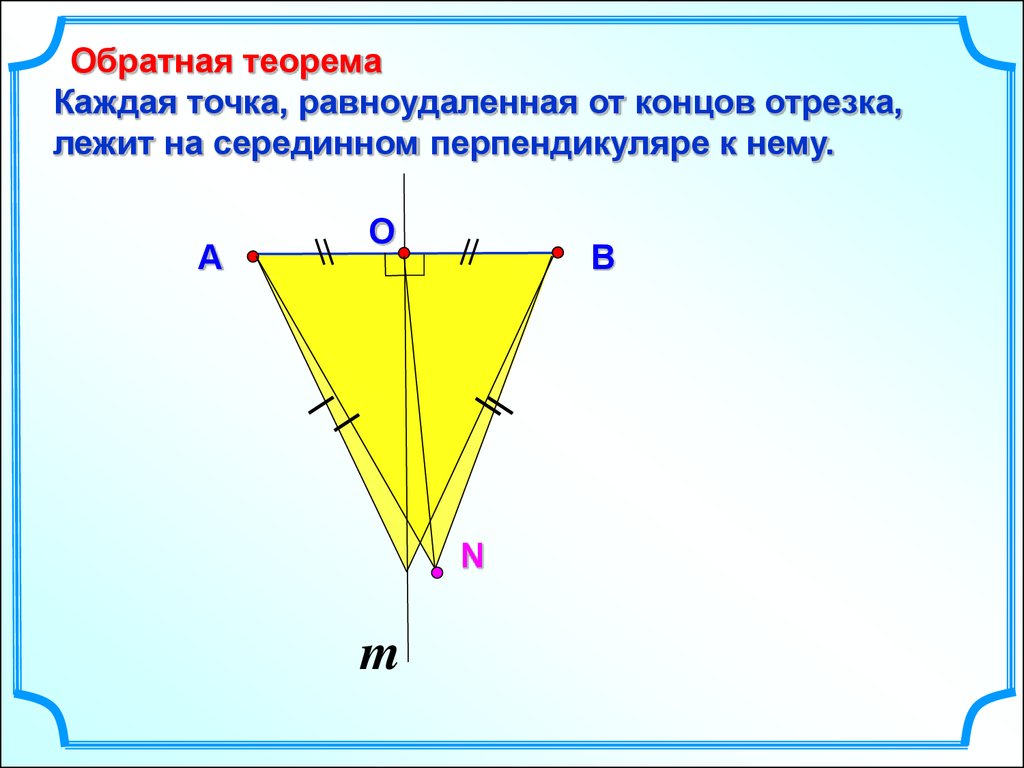
8.

Обратная теорема
Каждая точка, равноудаленная от концов отрезка,
лежит на серединном перпендикуляре к нему.
A
O
B
N
m

9.

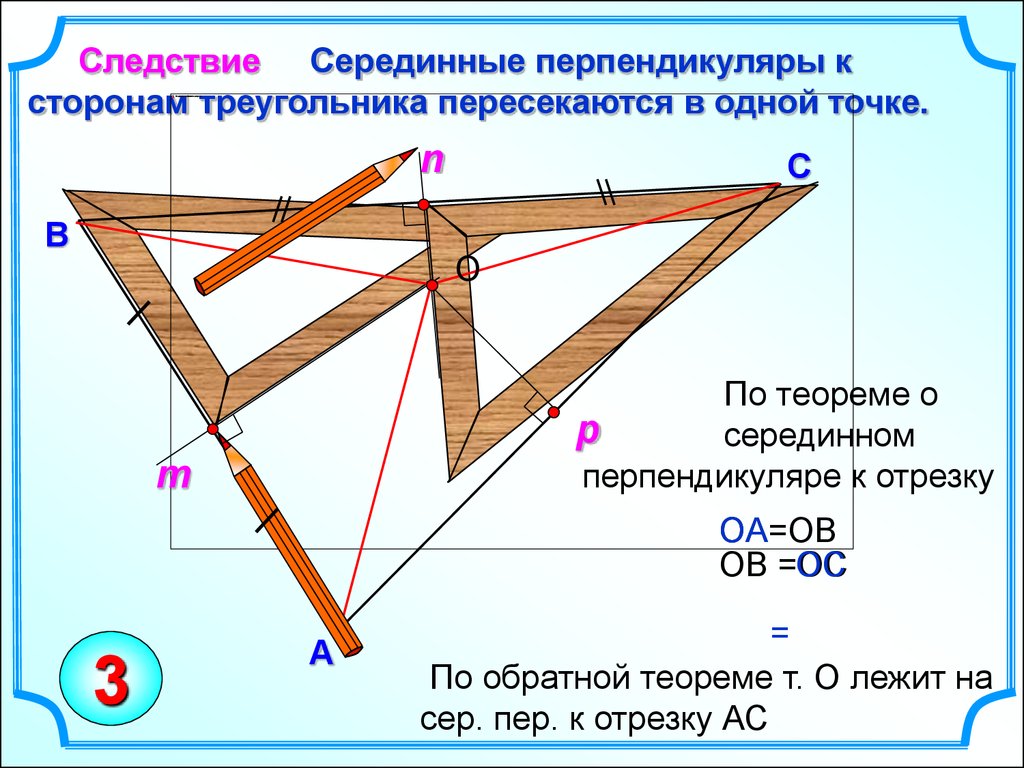
Следствие Серединные перпендикуляры к
сторонам треугольника пересекаются в одной точке.
n
B
C
О
По теореме о
р
серединном
перпендикуляре к отрезку
m
ОA
ОA=ОB
ОB =ОC
ОC
3
A
=
По обратной теореме т. О лежит на
сер. пер. к отрезку АС

10.

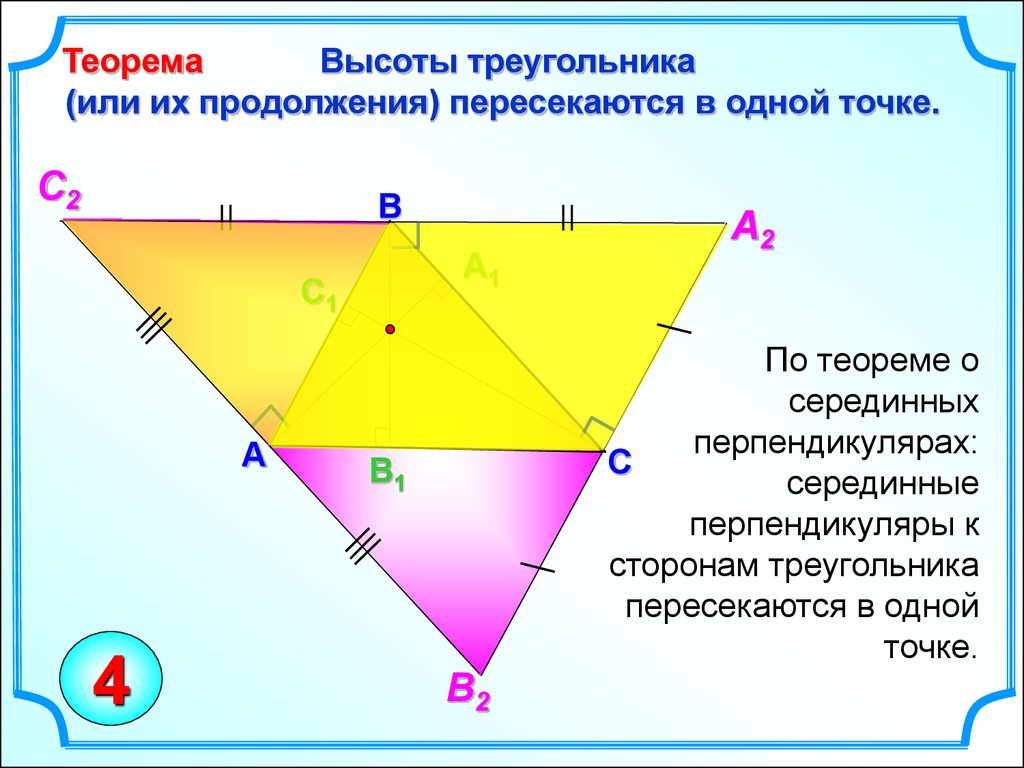
Теорема
Высоты треугольника
(или их продолжения) пересекаются в одной точке.
С2
B
A1
С1
A
4
В1
В2
А2
По теореме о
серединных
перпендикулярах:
C
серединные
перпендикуляры к
сторонам треугольника
пересекаются в одной
точке.

11.

Точка
пересечения
Точка
пересечения
Замечательные
точки
треугольника.
Точка
пересечения
Точка
пересечения
серединных

12.

Треугольник, который опирается на острие иглы в точке
пересечения медиан, находится в равновесии!
Точка, обладающая таким свойством, называется
центром тяжести треугольника.

13.

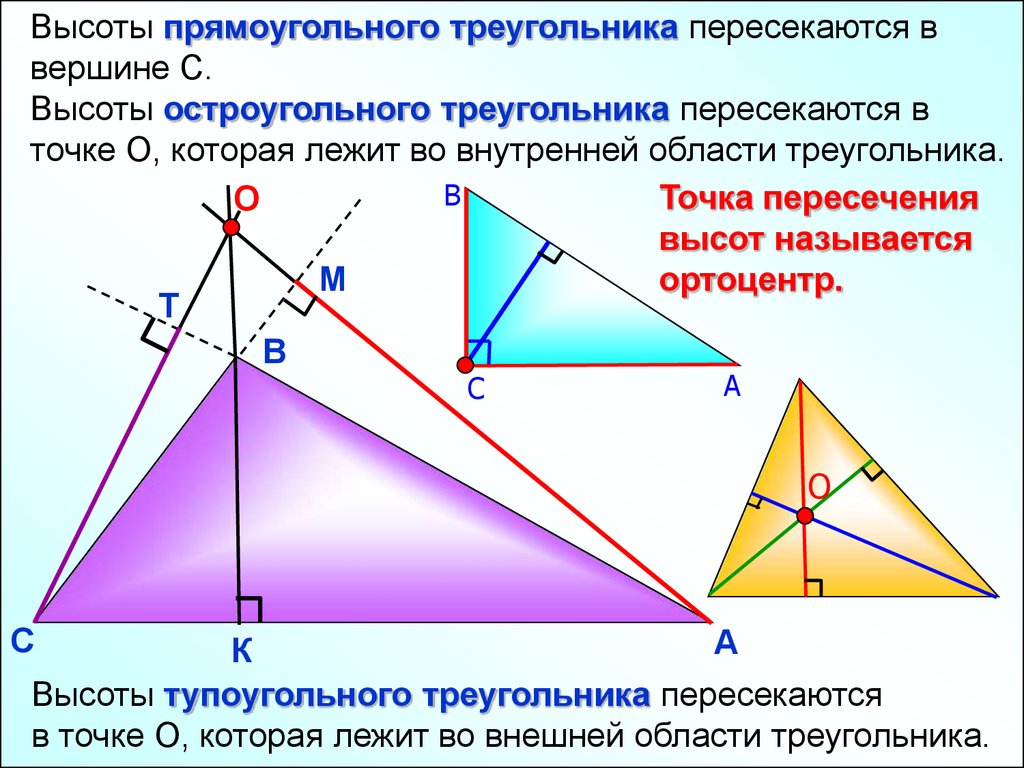
Высоты прямоугольного треугольника пересекаются в
вершине С.
Высоты остроугольного треугольника пересекаются в
точке О, которая лежит во внутренней области треугольника.
В
Точка пересечения
O
высот называется
М
ортоцентр.
Т
В
С
А
O
С
А
К
Высоты тупоугольного треугольника пересекаются
в точке О, которая лежит во внешней области треугольника.

14.

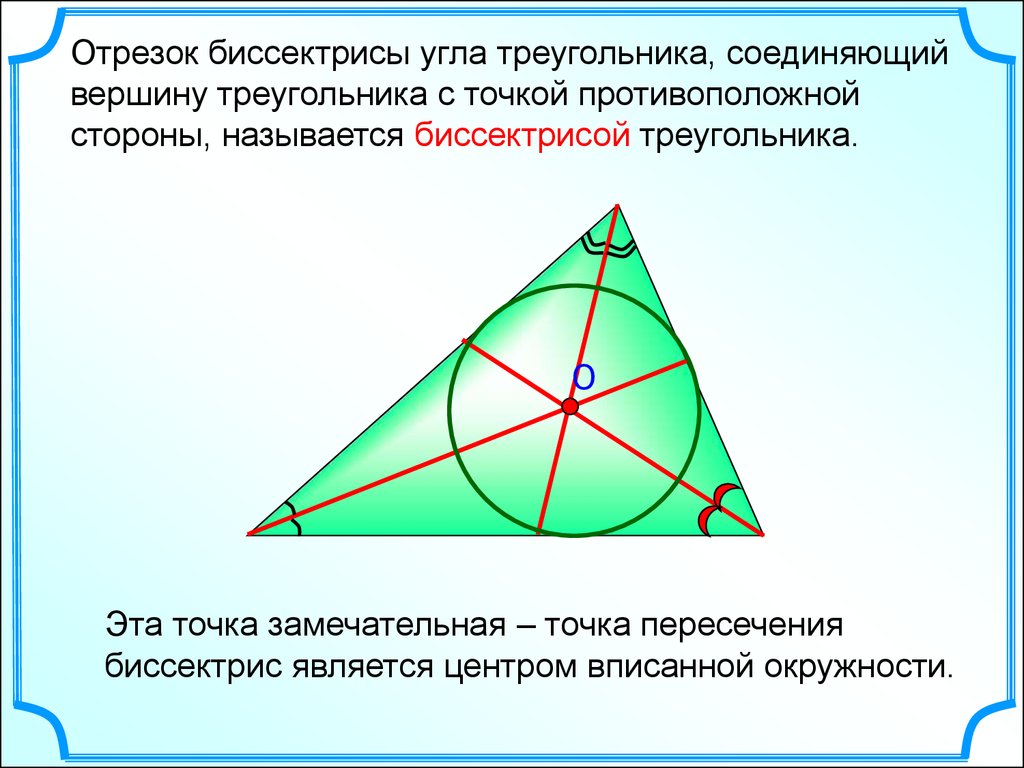
Отрезок биссектрисы угла треугольника, соединяющий
вершину треугольника с точкой противоположной
стороны, называется биссектрисой треугольника.
O
Эта точка замечательная – точка пересечения
биссектрис является центром вписанной окружности.

15.

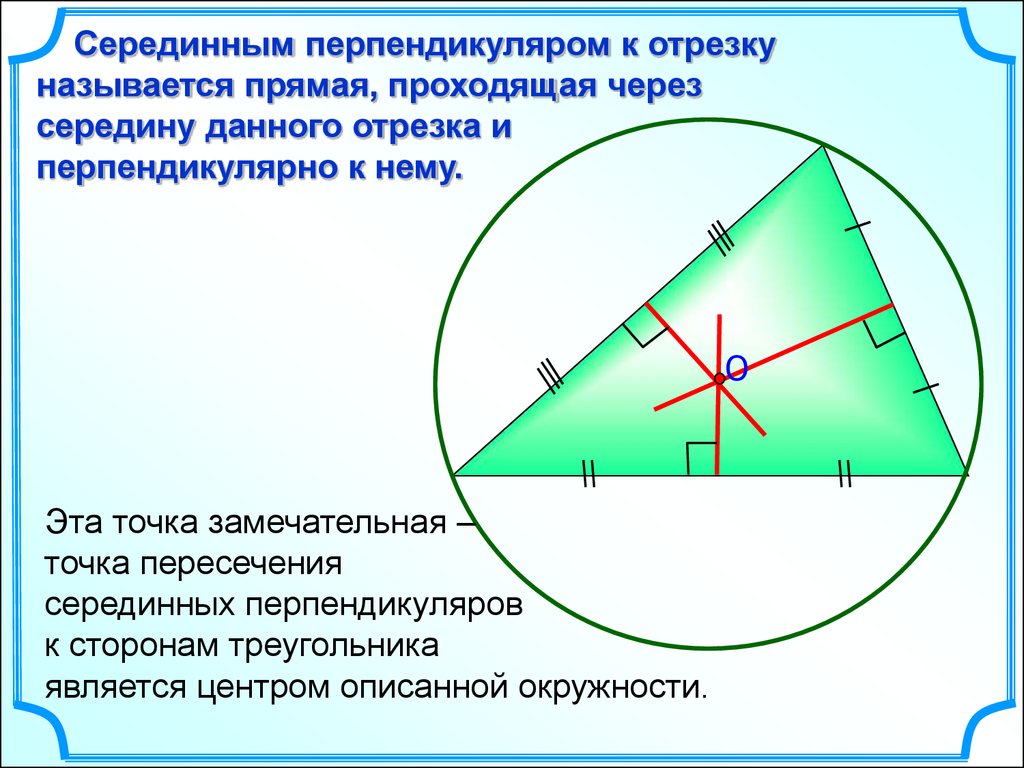
Серединным перпендикуляром к отрезку
называется прямая, проходящая через
середину данного отрезка и
перпендикулярно к нему.
O
Эта точка замечательная –
точка пересечения
серединных перпендикуляров
к сторонам треугольника
является центром описанной окружности.