Четыре замечательные точки треугольника

1.

Геометрия, 8 класс
© Кугушева Наталья Львовна, 2009

2.

Точка пересечения медиан треугольника
Точка пересечения биссектрис
треугольника
Точка пересечения высот
треугольника
Точка пересечения серединных
перпендикуляров треугольника

3.

Медиана
В
Медианой (BD) треугольника
называется отрезок, который соединяет
вершину треугольника с серединой
противолежащей стороны.
А
D
С

4.

Медианы треугольника пересекаются
в одной точке (центре тяжести
треугольника) и делятся этой точкой в
отношении 2 : 1, считая от вершины .
АМ : МА1 = ВМ : МВ1 = СМ :МС1 = 2 :1.
В
С1
М
А1
А
В1
С

5.

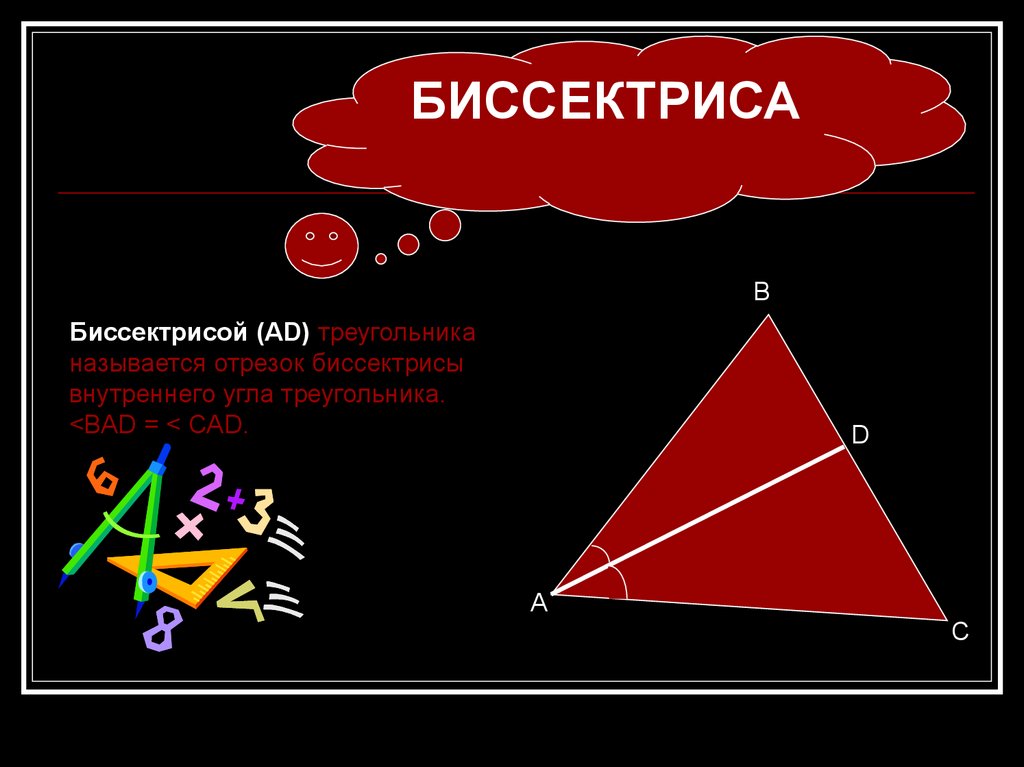
БИССЕКТРИСА
В
Биссектрисой (АD) треугольника
называется отрезок биссектрисы
внутреннего угла треугольника.
<BAD = < CAD.
D
A
C

6.

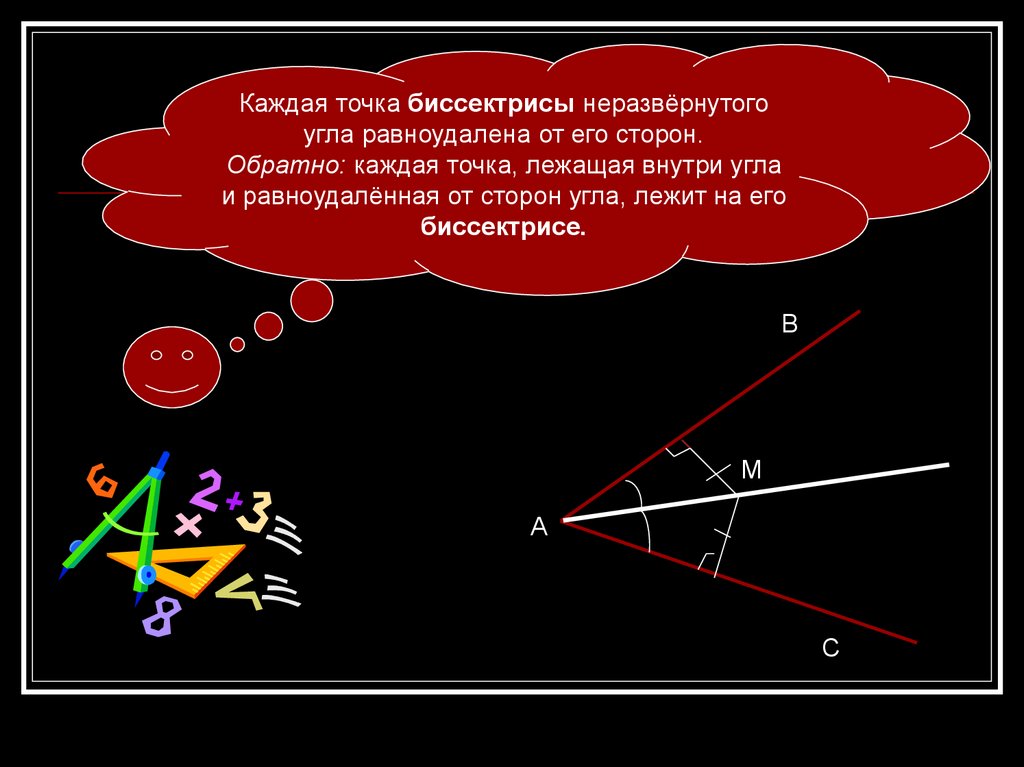
Каждая точка биссектрисы неразвёрнутого
угла равноудалена от его сторон.
Обратно: каждая точка, лежащая внутри угла
и равноудалённая от сторон угла, лежит на его
биссектрисе.
В
М
А
С

7.

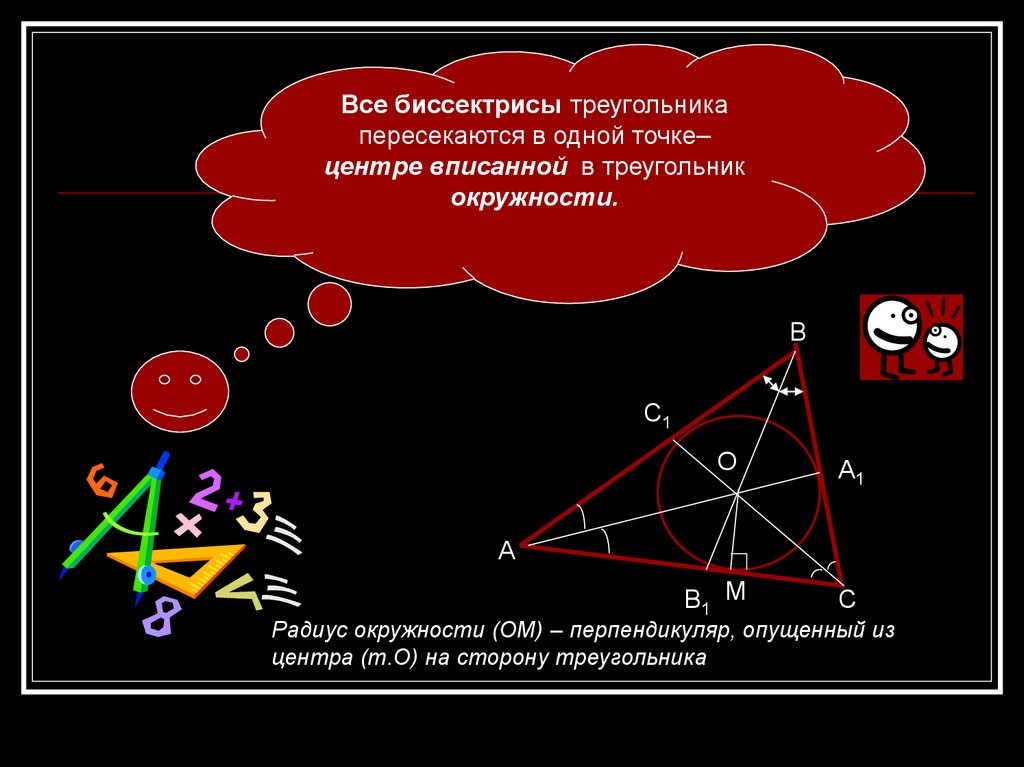
Все биссектрисы треугольника
пересекаются в одной точке–
центре вписанной в треугольник
окружности.
В
С1
О
А1
А
В1 М
С
Радиус окружности (ОМ) – перпендикуляр, опущенный из
центра (т.О) на сторону треугольника

8.

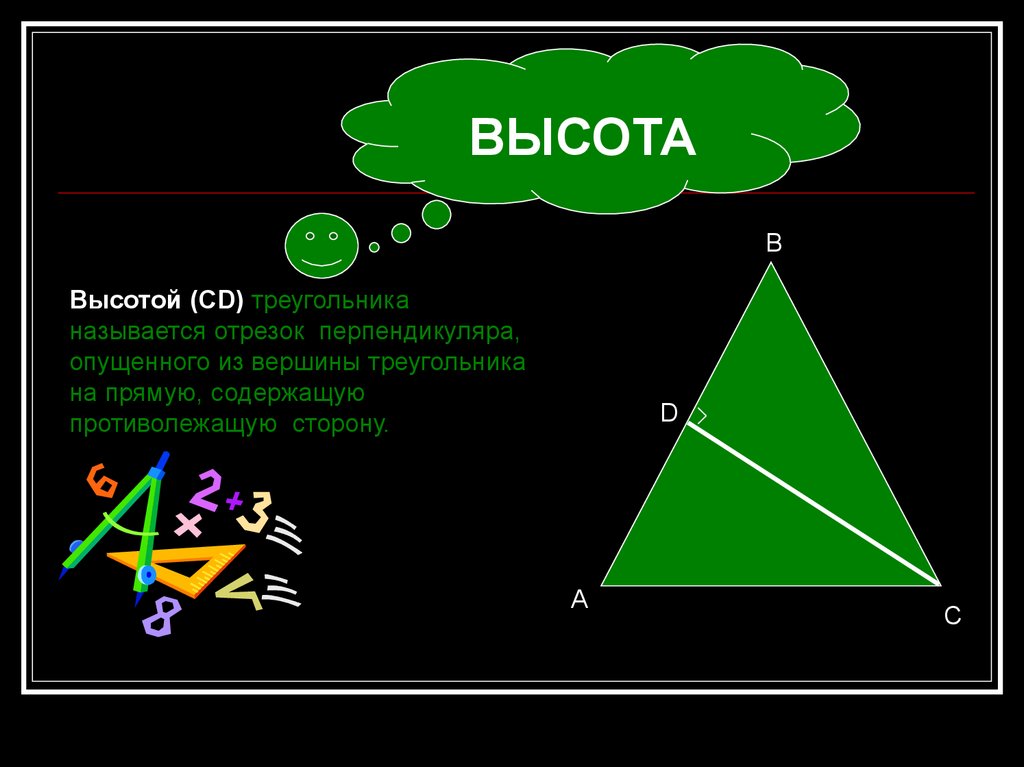
ВЫСОТА
B
Высотой (СD) треугольника
называется отрезок перпендикуляра,
опущенного из вершины треугольника
на прямую, содержащую
противолежащую сторону.
D
A
C

9.

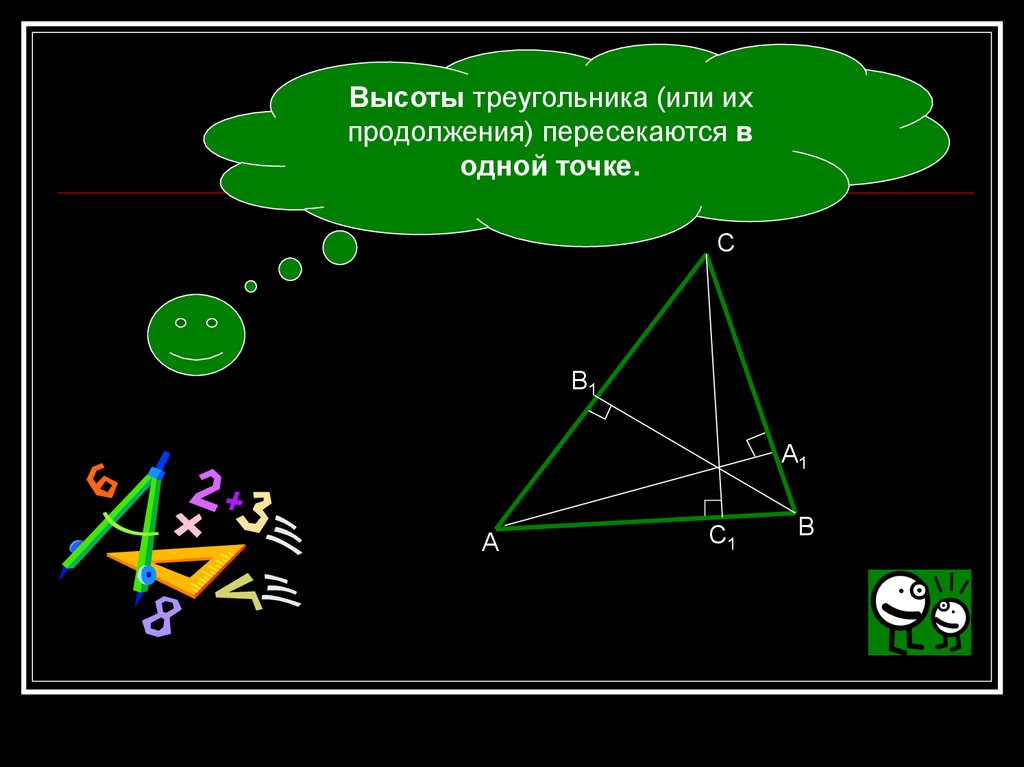
Высоты треугольника (или их
продолжения) пересекаются в
одной точке.
С
В1
А1
А
С1
В

10.

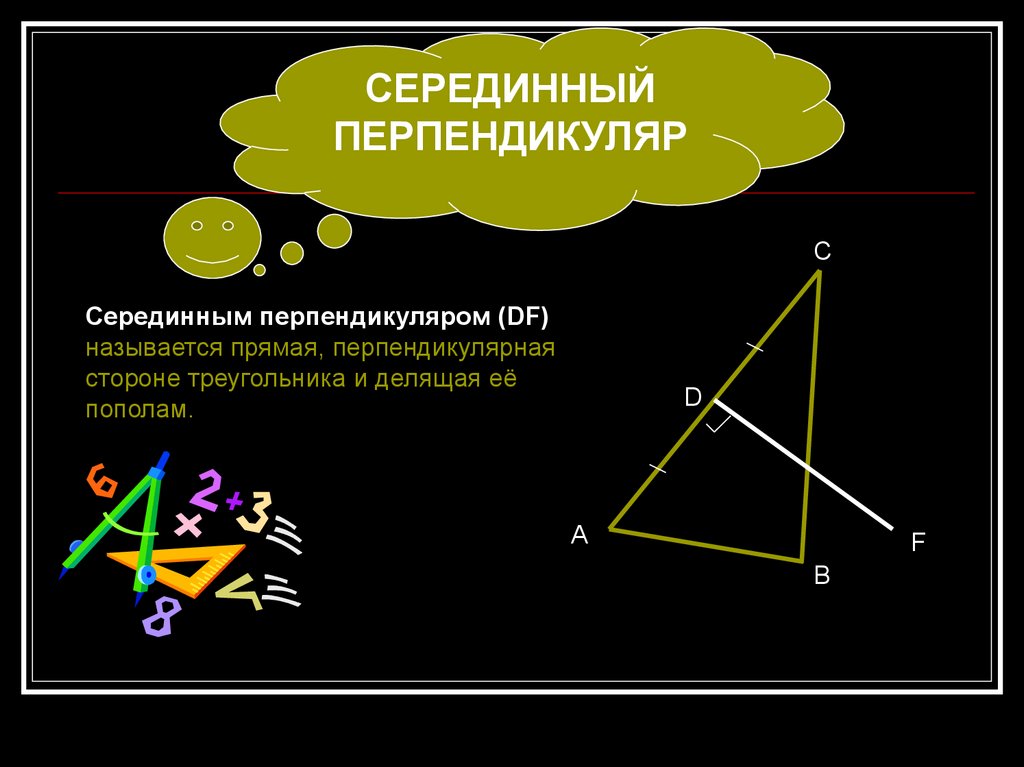
СЕРЕДИННЫЙ
ПЕРПЕНДИКУЛЯР
C
Серединным перпендикуляром (DF)
называется прямая, перпендикулярная
стороне треугольника и делящая её
пополам.
D
А
F
B

11.

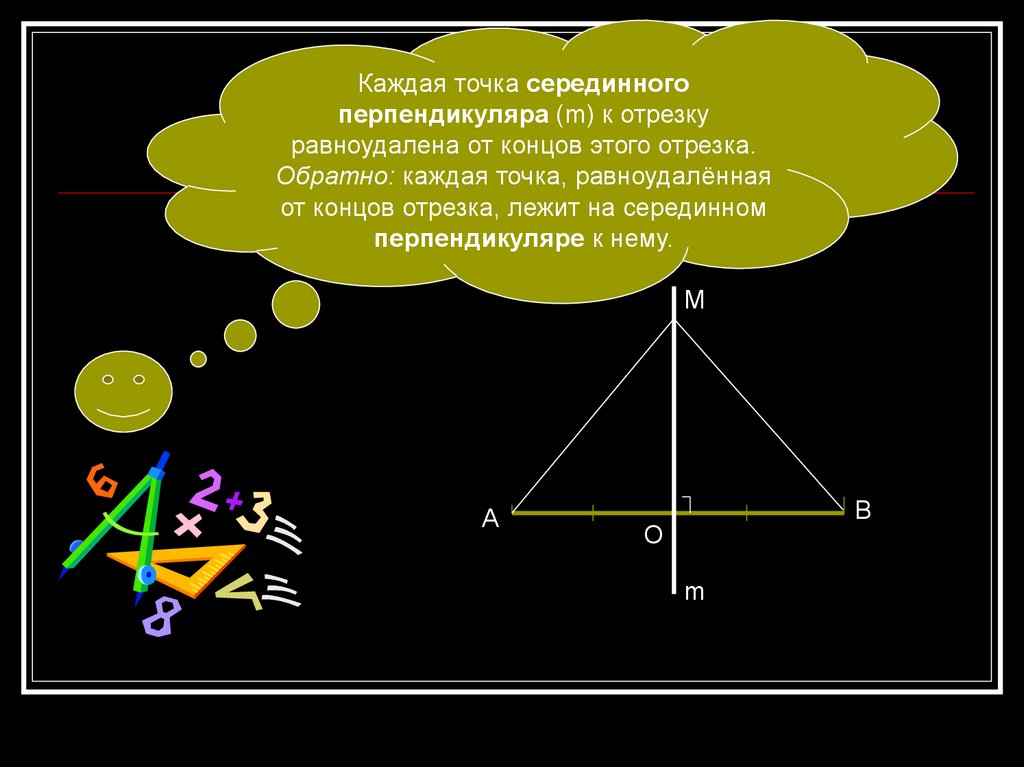
Каждая точка серединного
перпендикуляра (m) к отрезку
равноудалена от концов этого отрезка.
Обратно: каждая точка, равноудалённая
от концов отрезка, лежит на серединном
перпендикуляре к нему.
М
А
В
O
m

12.

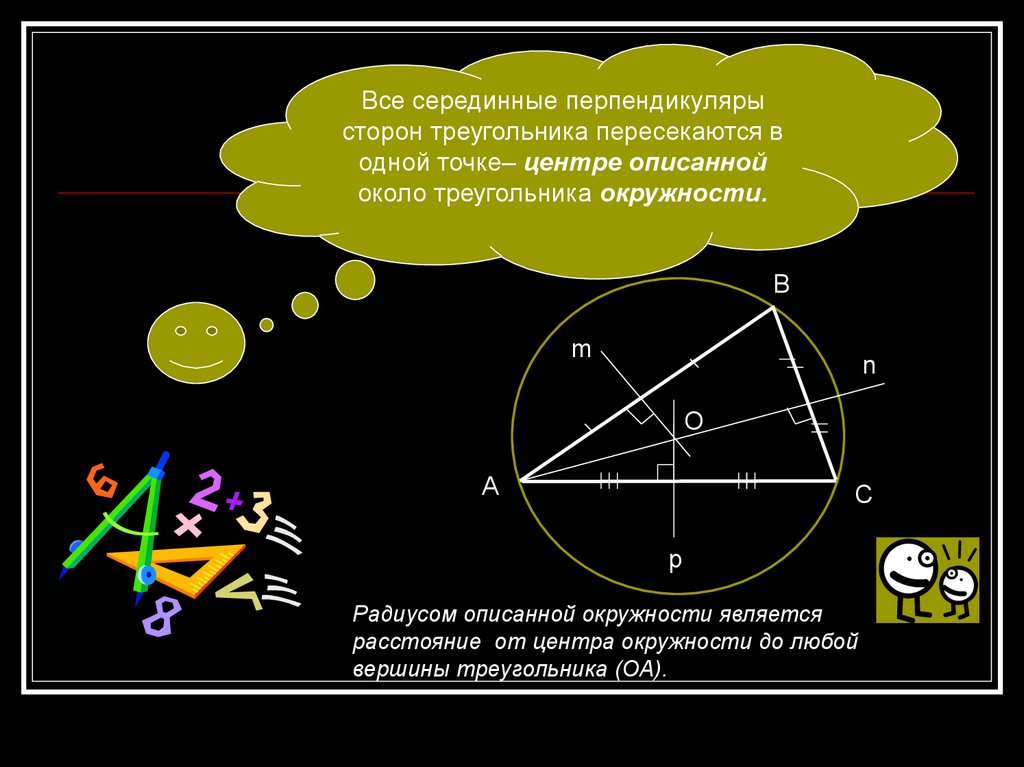
Все серединные перпендикуляры
сторон треугольника пересекаются в
одной точке– центре описанной
около треугольника окружности.
В
m
n
О
А
С
p
Радиусом описанной окружности является
расстояние от центра окружности до любой
вершины треугольника (ОА).

13.

Задания для учащихся
1. Постройте с помощью циркуля и
линейки окружность, вписанную в
тупоугольный треугольник.
Для этого:
•Постройте биссектрисы в тупоугольном
треугольнике с помощью циркуля и линейки.
Точка пересечения биссектрис– центр
окружности.
•Постройте радиус окружности:
перпендикуляр из центра окружности на
сторону треугольника.
•Постройте окружность, вписанную в
треугольник.

14.

2. Постройте с помощью циркуля и
линейки окружность, описанную
около тупоугольного треугольника.
Для этого:
•Постройте серединные перпендикуляры к
сторонам тупоугольного треугольника.
Точка пересечения этих перпендикуляров–
центр описанной окружности.
•Радиус окружности– расстояние от центра
до любой вершины треугольника.
•Постройте окружность, описанную около
треугольника.