Четыре замечательные точки треугольника

1.

Четыре
замечательные
точки
треугольника

2. Четыре замечательные точки треугольника

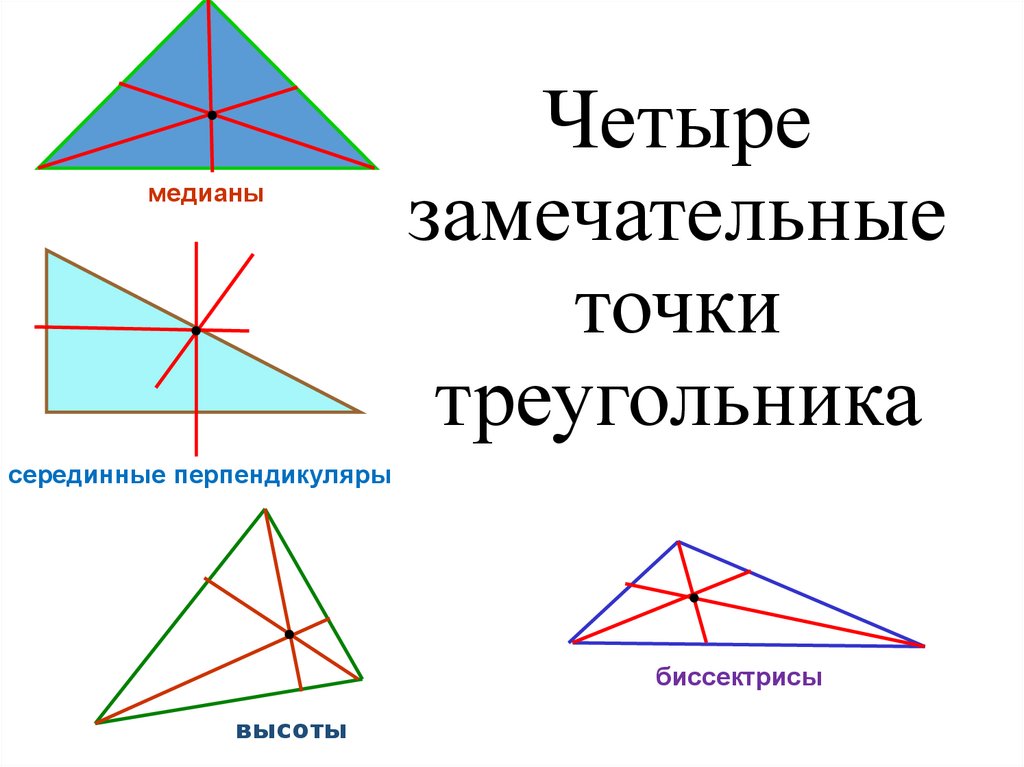
медианы
Четыре
замечательные
точки
треугольника
серединные перпендикуляры
биссектрисы
высоты

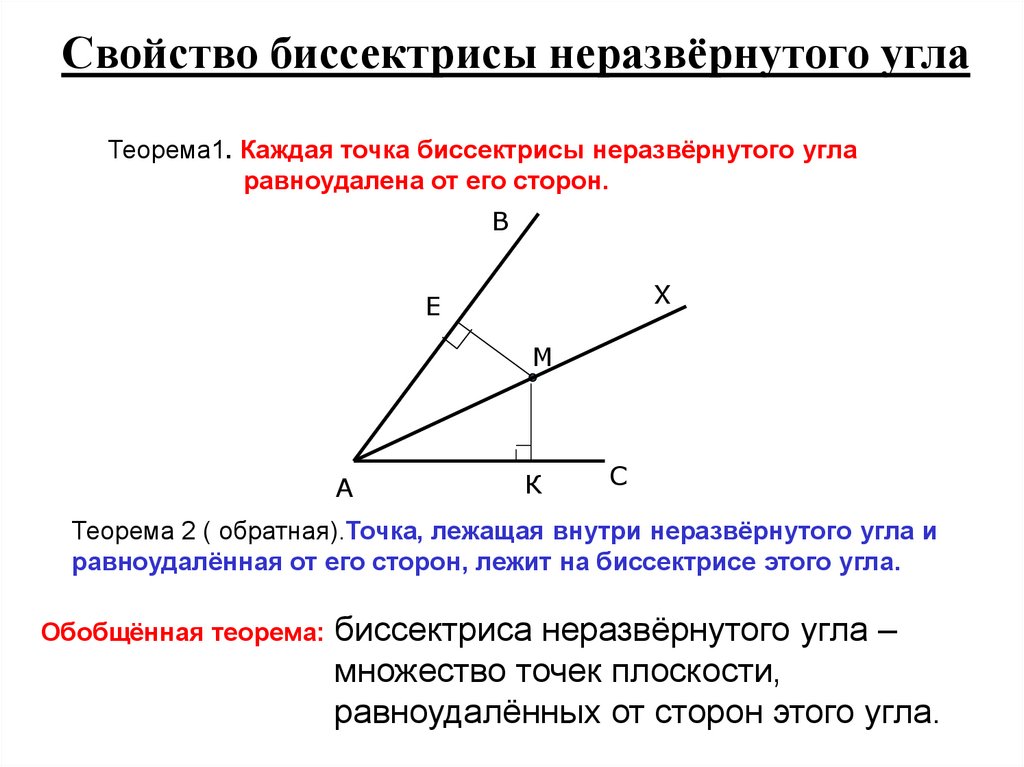
3. Свойство биссектрисы неразвёрнутого угла

Теорема1. Каждая точка биссектрисы неразвёрнутого угла
равноудалена от его сторон.
В
Х
Е
М
А
К
С
Теорема 2 ( обратная).Точка, лежащая внутри неразвёрнутого угла и
равноудалённая от его сторон, лежит на биссектрисе этого угла.
Обобщённая теорема:
биссектриса неразвёрнутого угла –
множество точек плоскости,
равноудалённых от сторон этого угла.

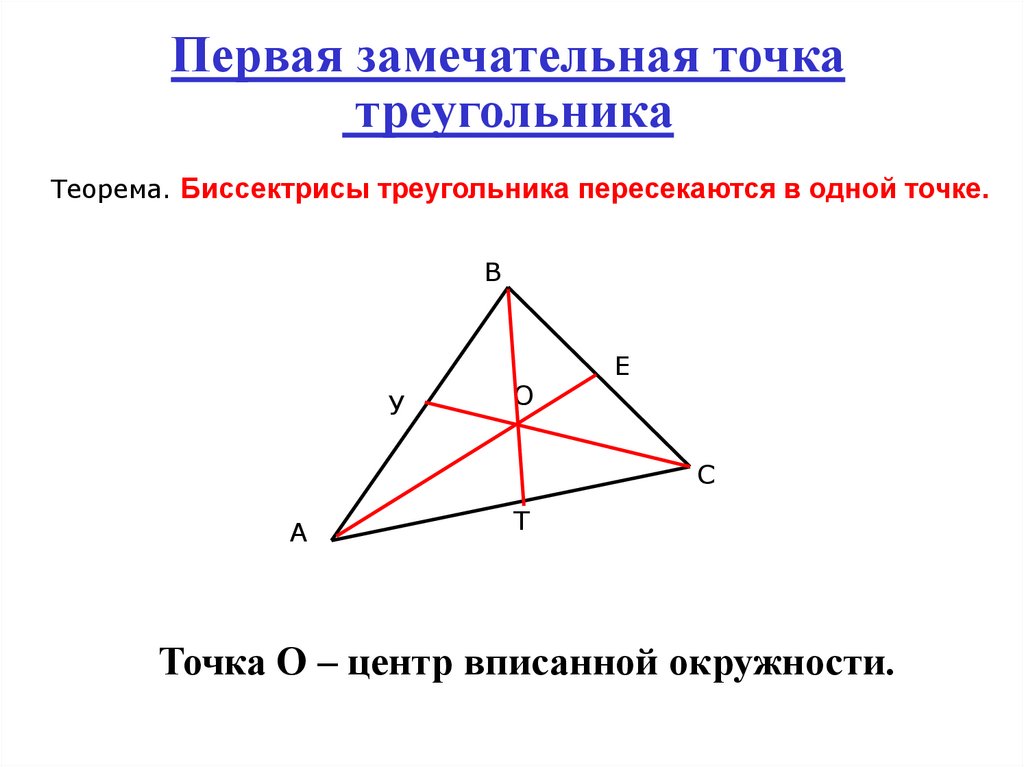
4. Первая замечательная точка треугольника

Теорема. Биссектрисы треугольника пересекаются в одной точке.
В
У
О
Е
С
А
Т
Точка О – центр вписанной окружности.

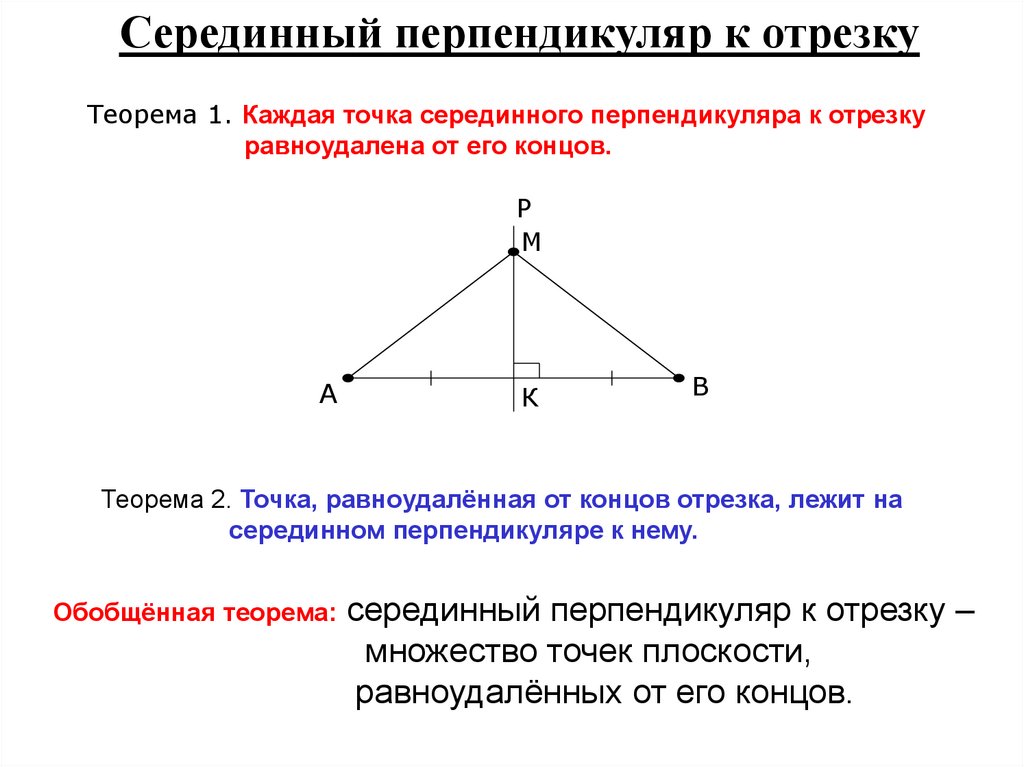
5. Серединный перпендикуляр к отрезку

Теорема 1. Каждая точка серединного перпендикуляра к отрезку
равноудалена от его концов.
Р
М
А
К
В
Теорема 2. Точка, равноудалённая от концов отрезка, лежит на
серединном перпендикуляре к нему.
Обобщённая теорема:
серединный перпендикуляр к отрезку –
множество точек плоскости,
равноудалённых от его концов.

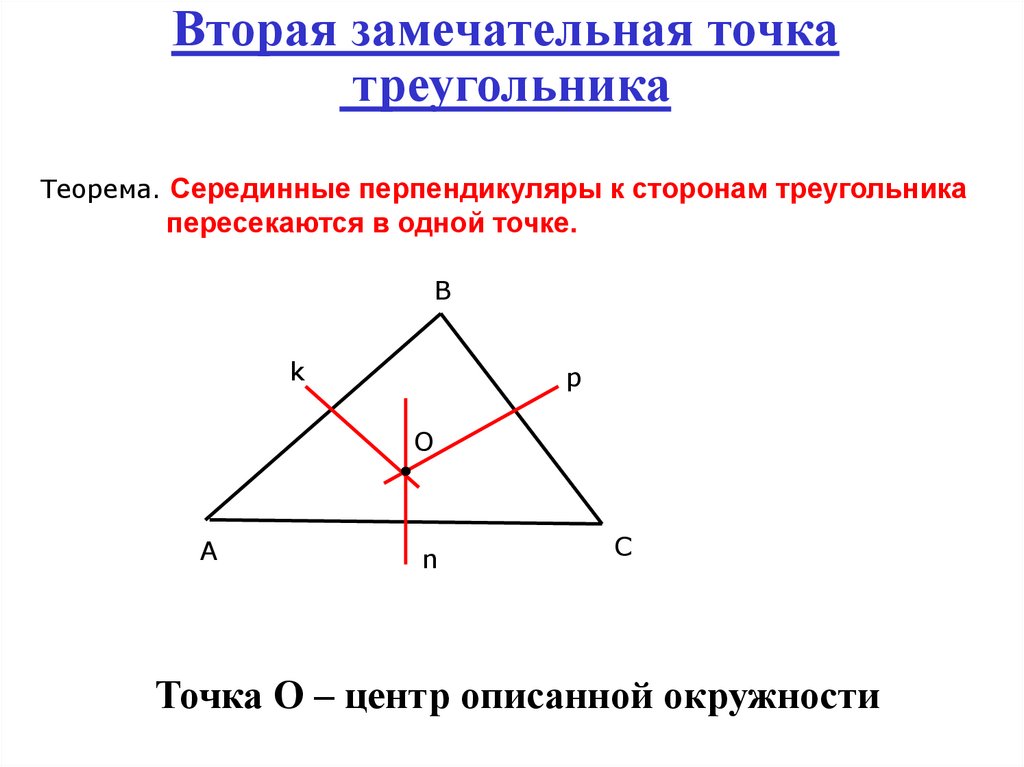
6. Вторая замечательная точка треугольника

Теорема. Серединные перпендикуляры к сторонам треугольника
пересекаются в одной точке.
В
k
p
О
А
n
С
Точка О – центр описанной окружности

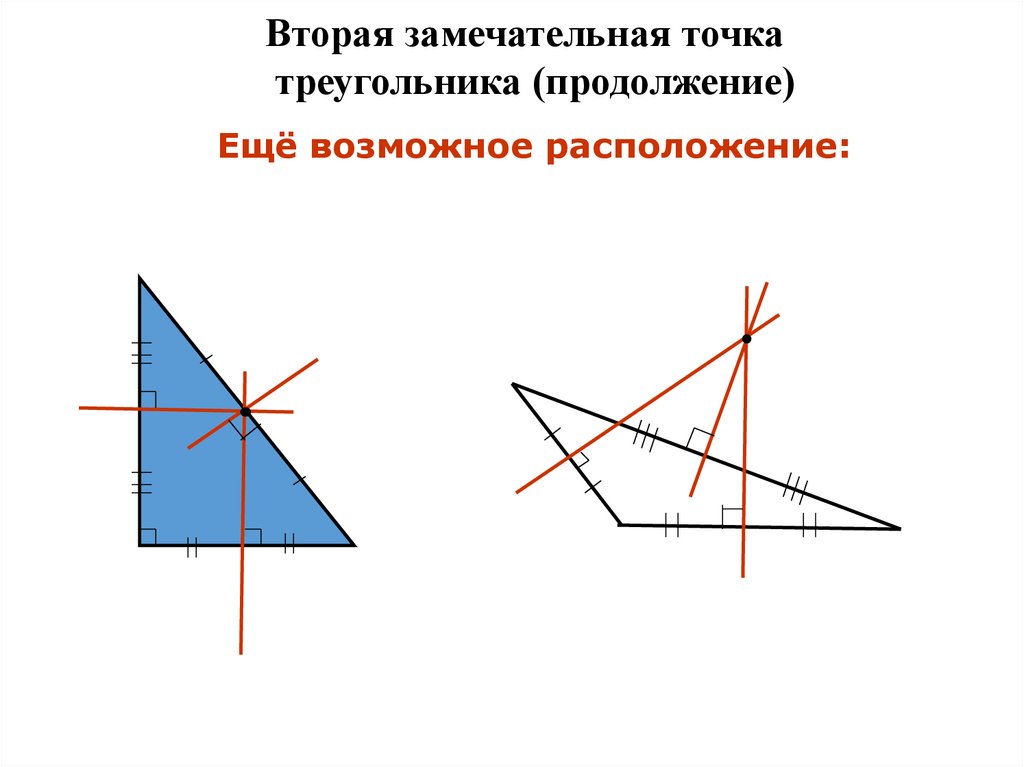
7.

Вторая замечательная точка
треугольника (продолжение)
Ещё возможное расположение:

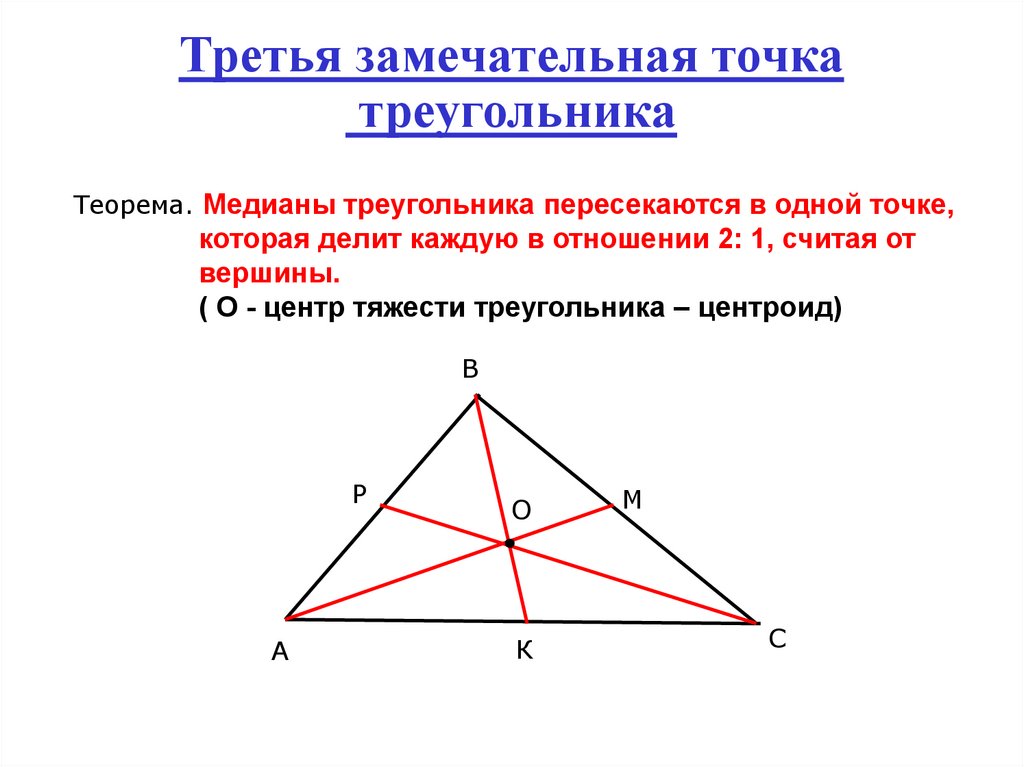
8. Третья замечательная точка треугольника

Теорема. Медианы треугольника пересекаются в одной точке,
которая делит каждую в отношении 2: 1, считая от
вершины.
( О - центр тяжести треугольника – центроид)
В
Р
А
О
К
М
С

9.

Треугольник, который опирается на острие иглы в
точке пересечения медиан, находится в
равновесии!
Точка пересечения медиан называется
центром тяжести треугольника.

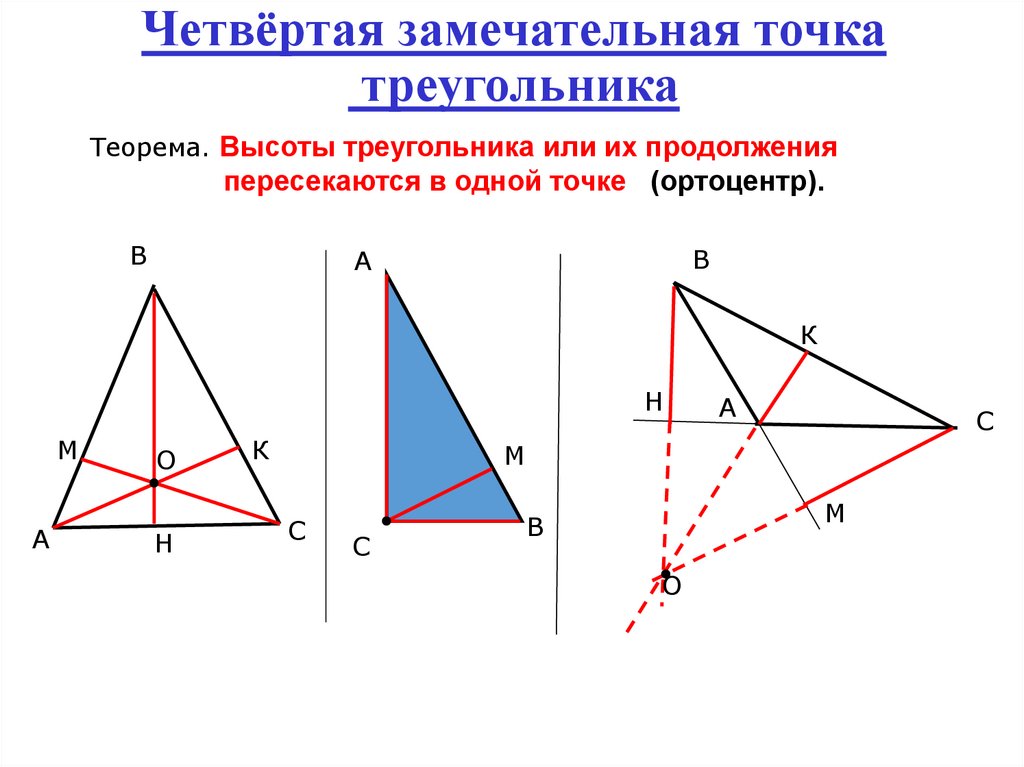
10. Четвёртая замечательная точка треугольника

Теорема. Высоты треугольника или их продолжения
пересекаются в одной точке (ортоцентр).
В
В
А
К
Н
М
А
О
Н
К
А
С
М
С
С
М
В
О

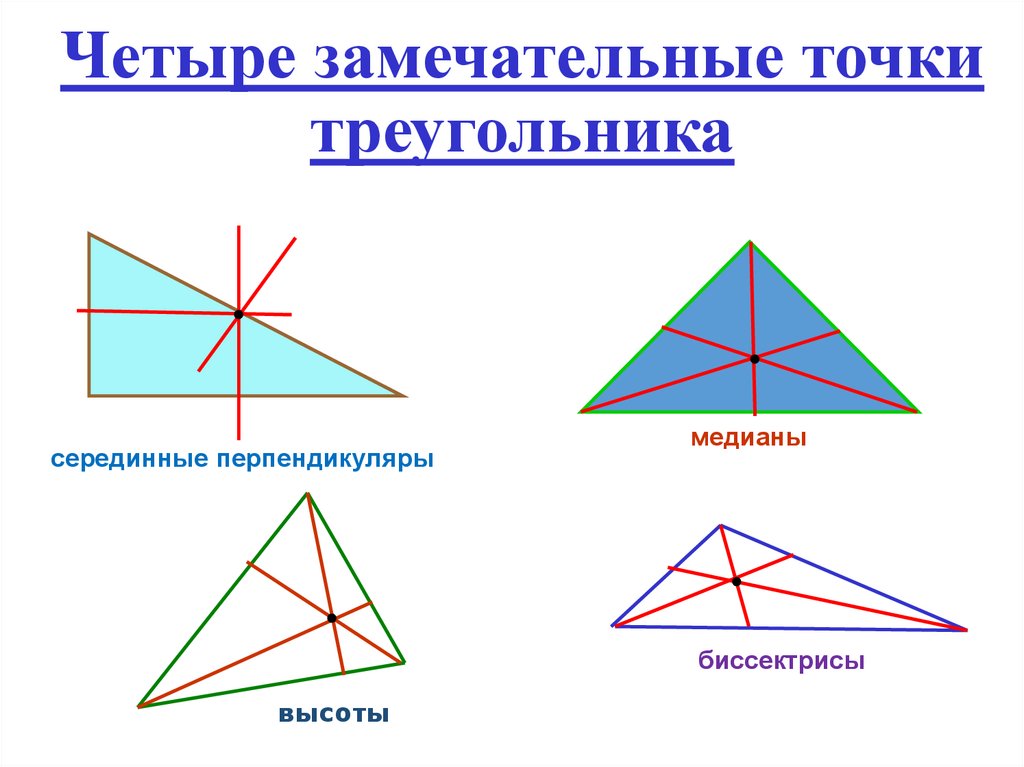
11. Четыре замечательные точки треугольника

серединные перпендикуляры
медианы
биссектрисы
высоты

12.

А

13.

А