Similar presentations:
Площадь усеченной пирамиды
1.
Усеченная пирамидаБоковые грани – трапеции
Теорема: Площадь боковой поверхности правильной
усеченной пирамиды равна половине произведения
полусуммы периметров оснований на апофему
Sбок. =
1
( Р1 Р2 ) d
2
2.
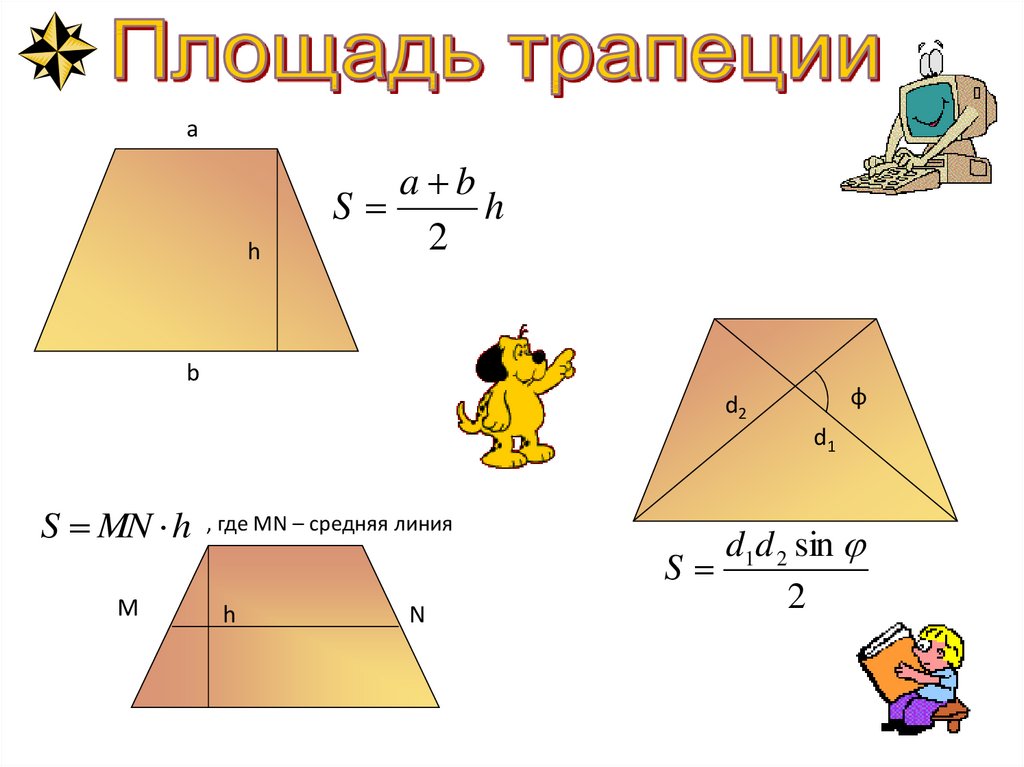
ah
a b
S
h
2
b
φ
d2
d1
S MN h
M
, где MN – средняя линия
h
N
d1d 2 sin
S
2
3.
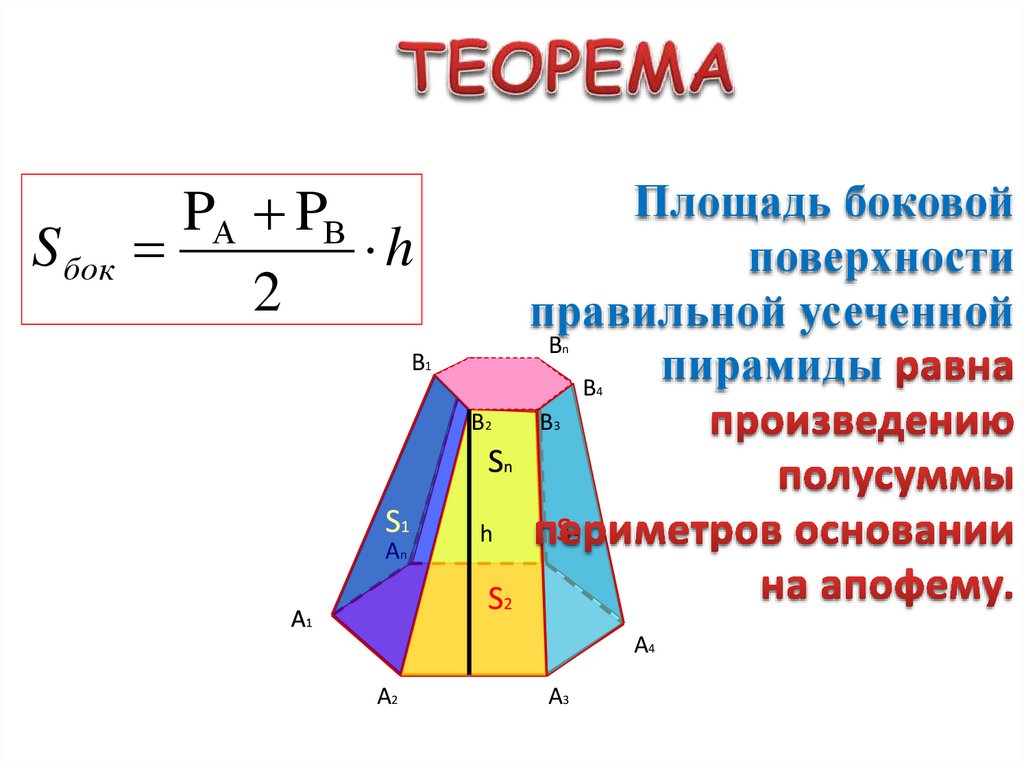
S бокPА PВ
h
2
Площадь боковой
поверхности
правильной усеченной
В
пирамиды
В
n
В1
4
В2
An
В3
h
A4
A2
A3
4. Решение задач на повторение
РЕШЕНИЕ ЗАДАЧНА
ПОВТОРЕНИЕ
5.
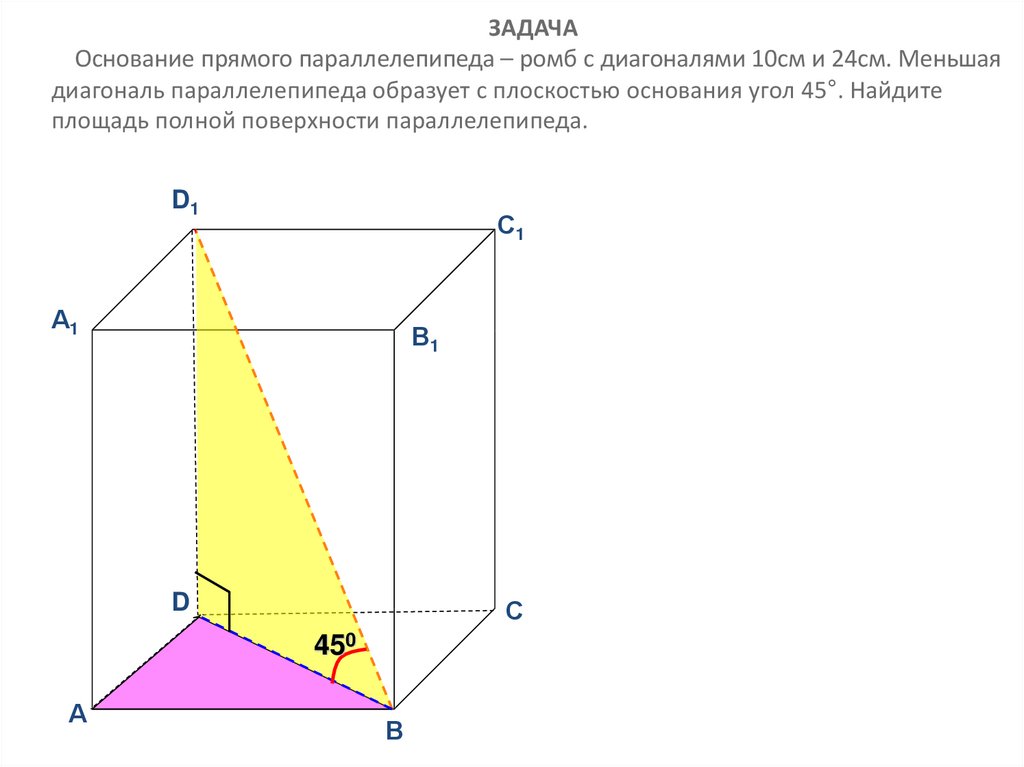
ЗАДАЧАОснование прямого параллелепипеда – ромб с диагоналями 10см и 24см. Меньшая
диагональ параллелепипеда образует с плоскостью основания угол 45°. Найдите
площадь полной поверхности параллелепипеда.
D1
С1
А1
В1
D
С
450
А
В
6.
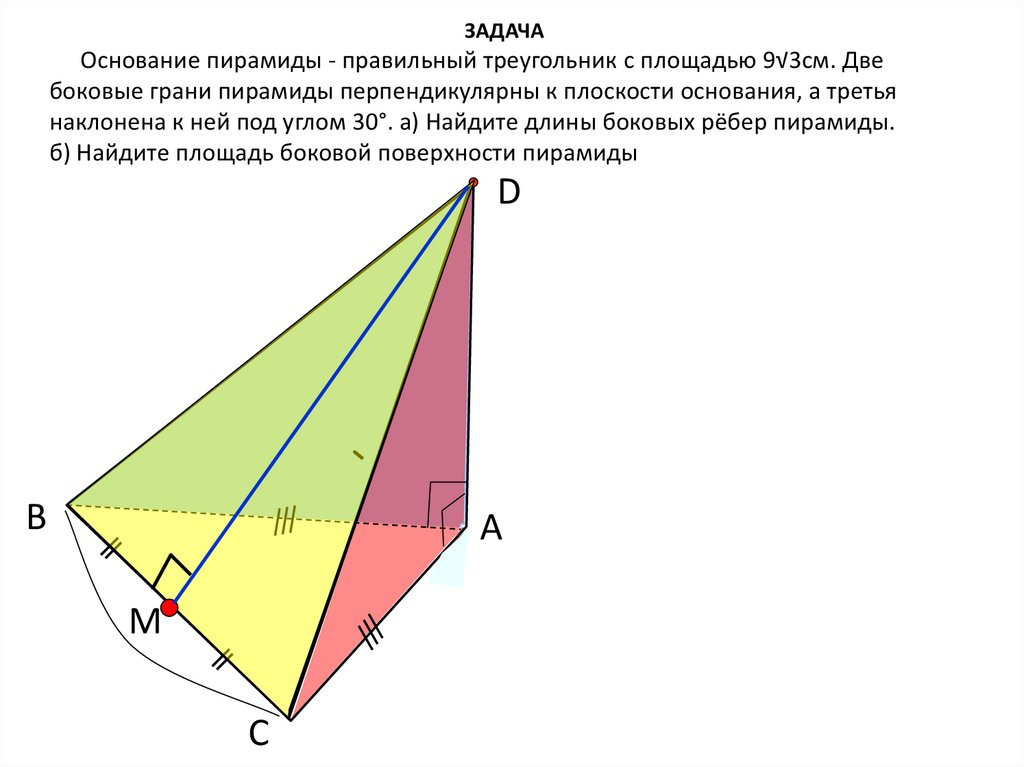
ЗАДАЧАОснование пирамиды - правильный треугольник с площадью 9√3см. Две
боковые грани пирамиды перпендикулярны к плоскости основания, а третья
наклонена к ней под углом 30°. а) Найдите длины боковых рёбер пирамиды.
б) Найдите площадь боковой поверхности пирамиды
D
В
А
M
С
7.
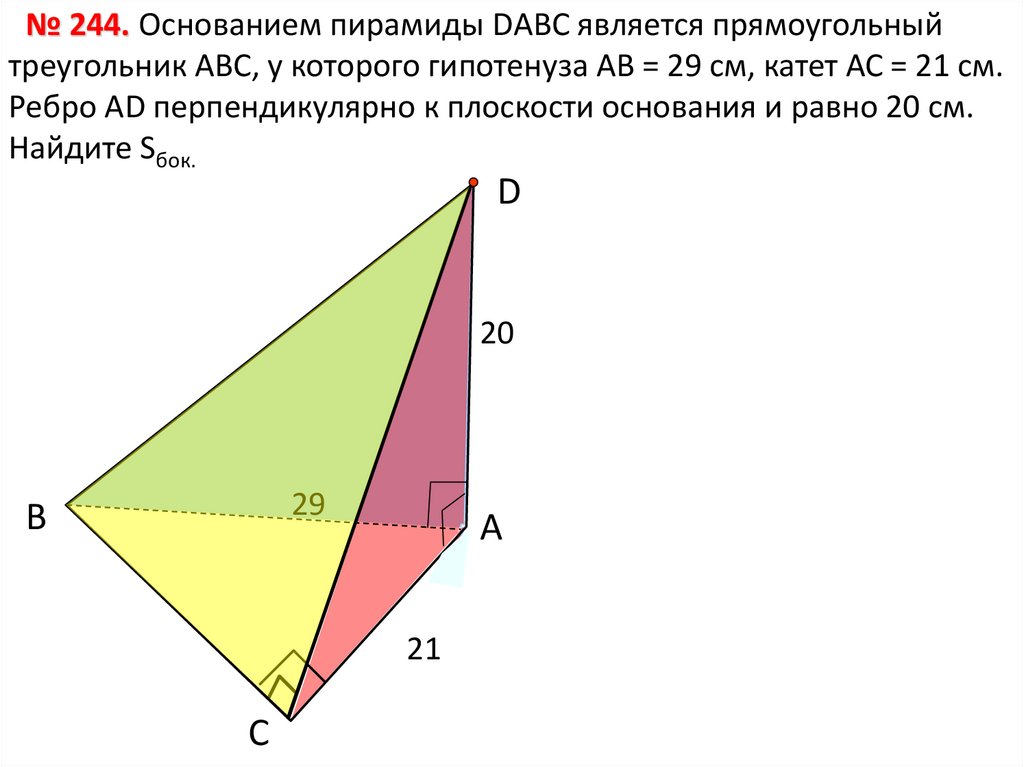
№ 244. Основанием пирамиды DАВС является прямоугольныйтреугольник АВС, у которого гипотенуза АВ = 29 см, катет АС = 21 см.
Ребро АD перпендикулярно к плоскости основания и равно 20 см.
Найдите Sбок.
D
20
29
В
А
21
С


 mathematics
mathematics








