Пирамида. Усеченная пирамида

1.

2.

3.

P
P
P
B
A
F
E
C
A
D
A
D
B
C
Пирамиды
B
C

4.

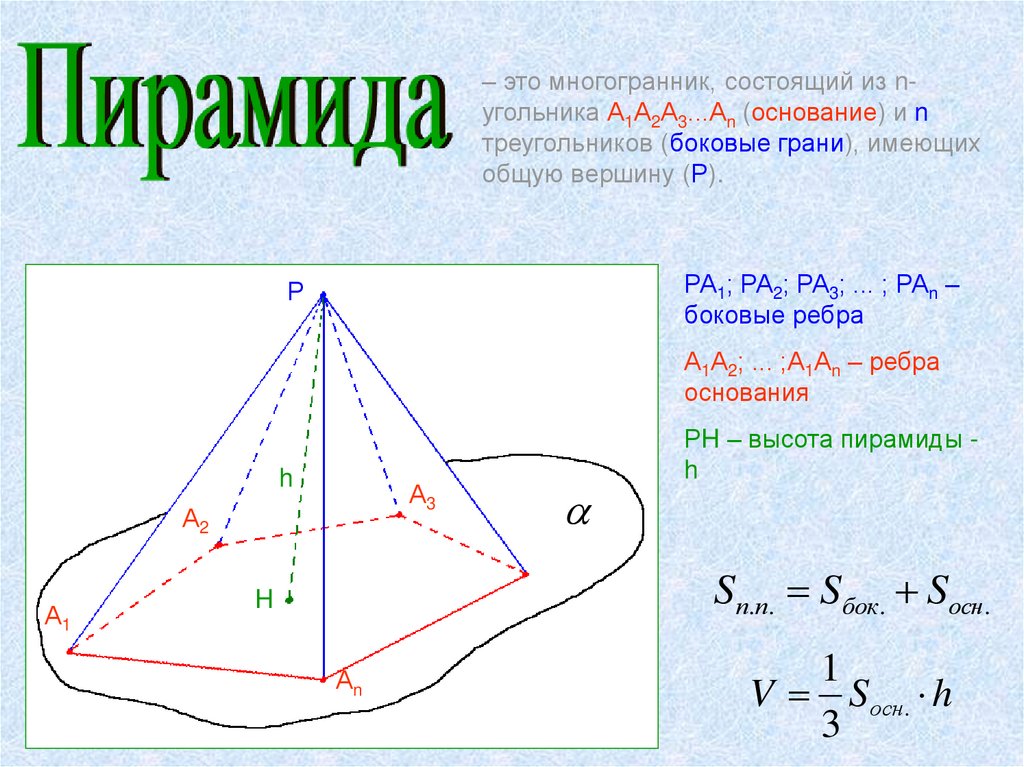
– это многогранник, состоящий из nугольника А1А2А3...Аn (основание) и n
треугольников (боковые грани), имеющих
общую вершину (Р).
РА1; РА2; РА3; ... ; РАn –
боковые ребра
Р
А1А2; ... ;А1Аn – ребра
основания
h
А3
А2
А1
РH – высота пирамиды h
Sп.п. Sбок. Sосн.
H
Аn
1
V Sосн. h
3

5.

P
D
A
O
PO ( ABC )
B
C

6.

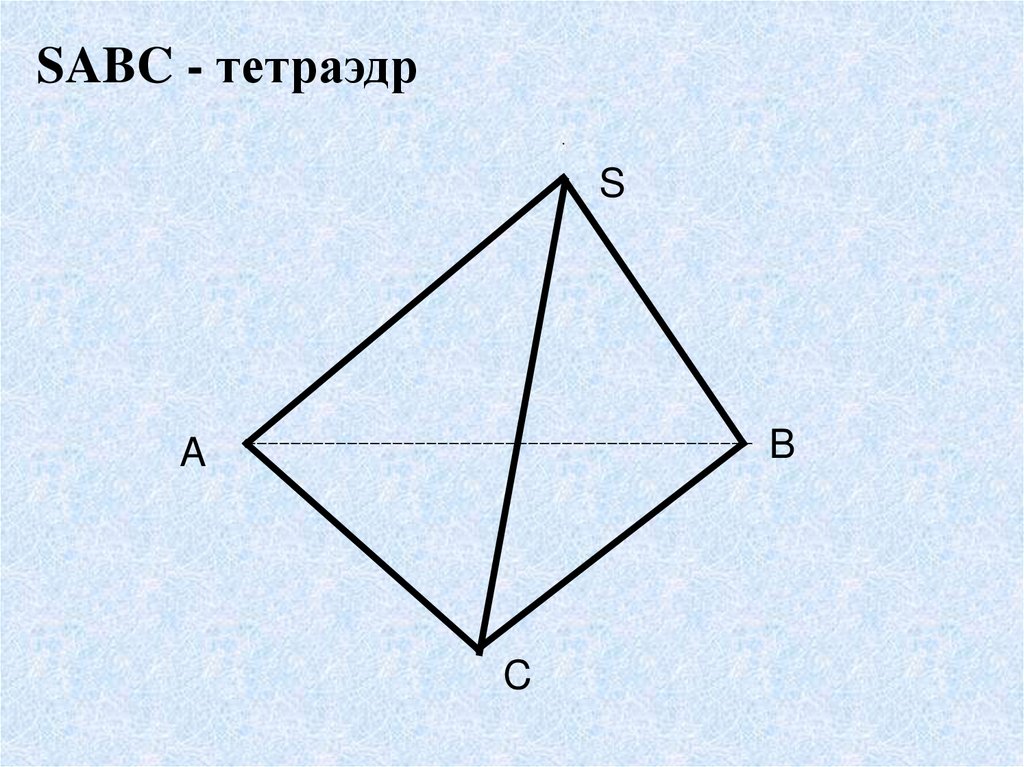
SABC - тетраэдр
S
B
A
C

7.

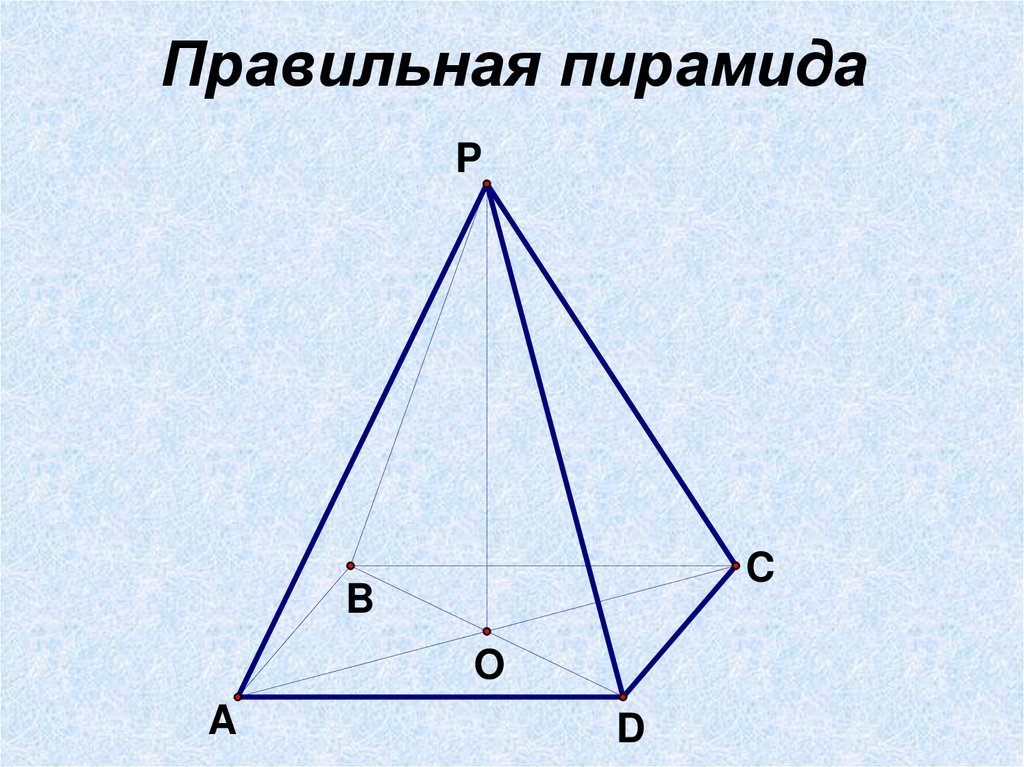
Правильная пирамида
P
C
B
O
A
D

8.

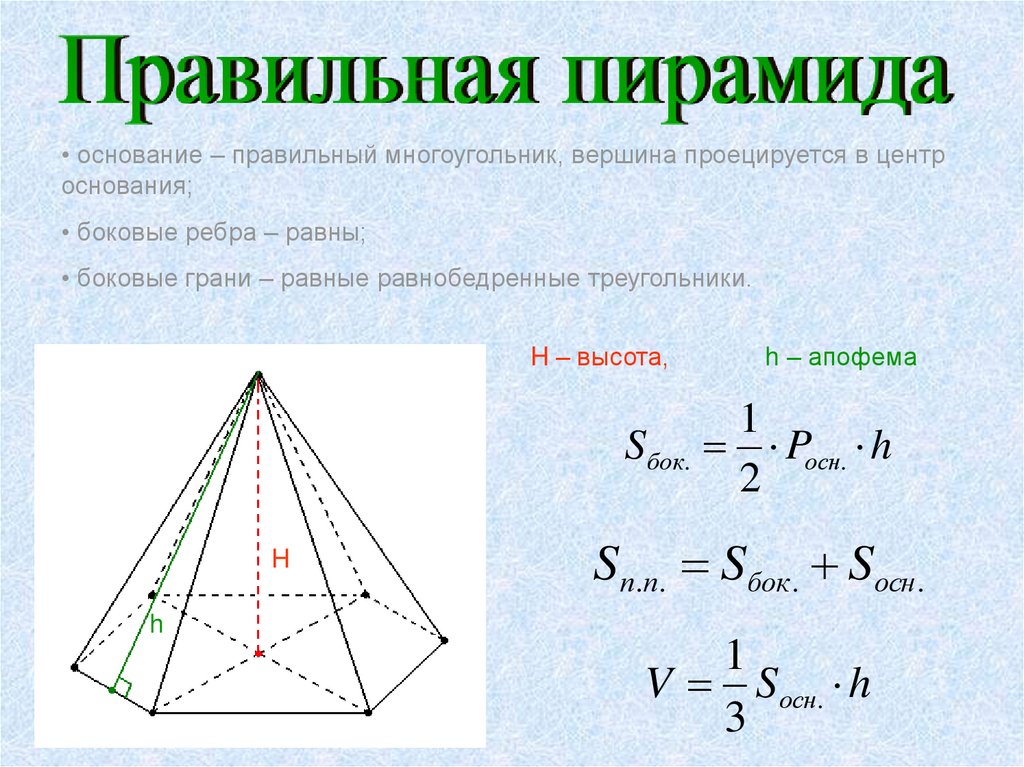
• основание – правильный многоугольник, вершина проецируется в центр
основания;
• боковые ребра – равны;
• боковые грани – равные равнобедренные треугольники.
H – высота,
h – апофема
1
Sбок. Pосн. h
2
H
Sп.п. Sбок. Sосн.
h
1
V Sосн. h
3

9.

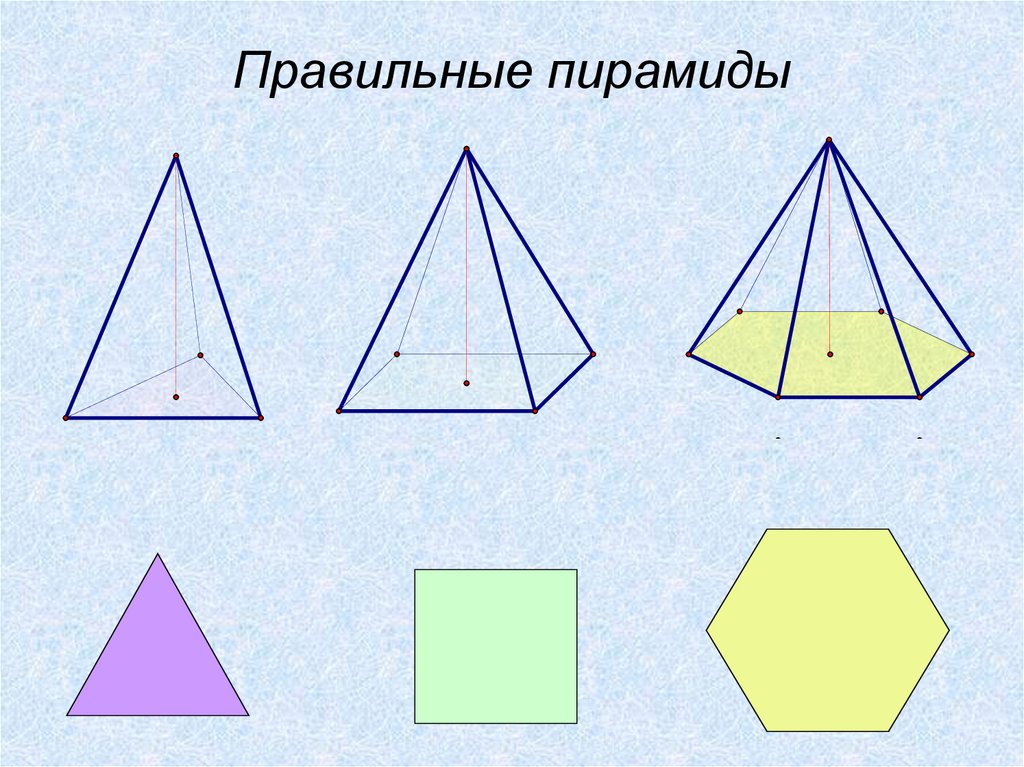
Правильные пирамиды

10.

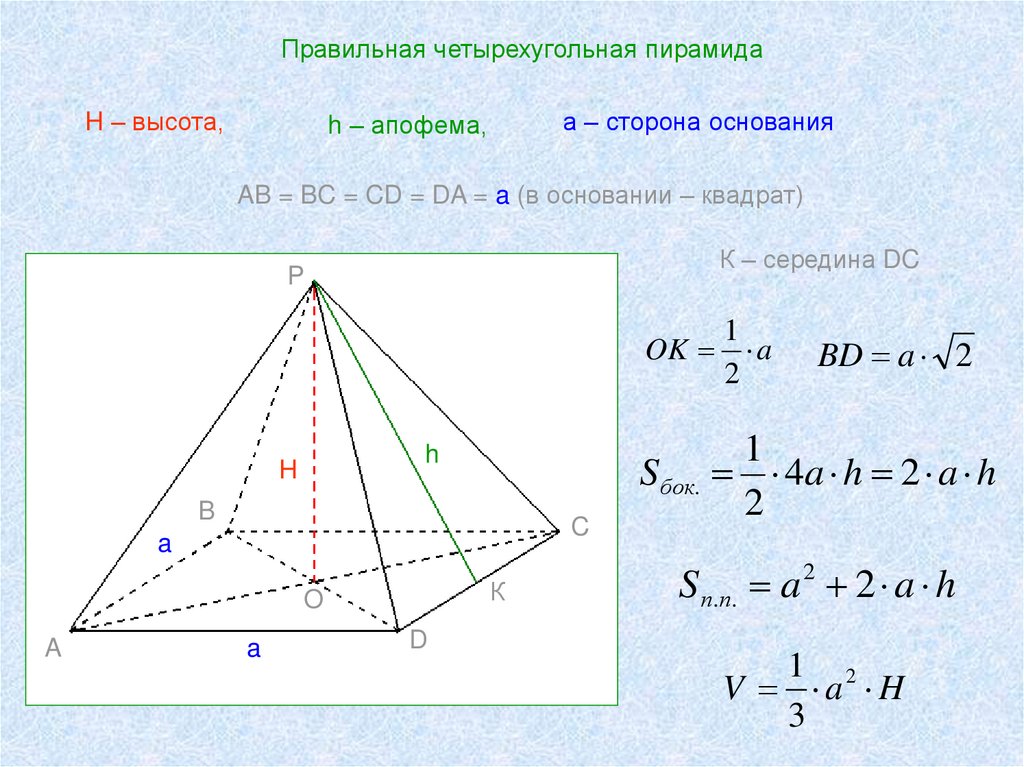
Правильная четырехугольная пирамида
H – высота,
а – сторона основания
h – апофема,
AB = BC = CD = DA = a (в основании – квадрат)
К – середина DC
P
1
OK a
2
h
H
B
C
a
К
O
A
a
D
BD a 2
1
Sбок. 4a h 2 a h
2
S п.п. a 2 2 a h
1 2
V a H
3

11.

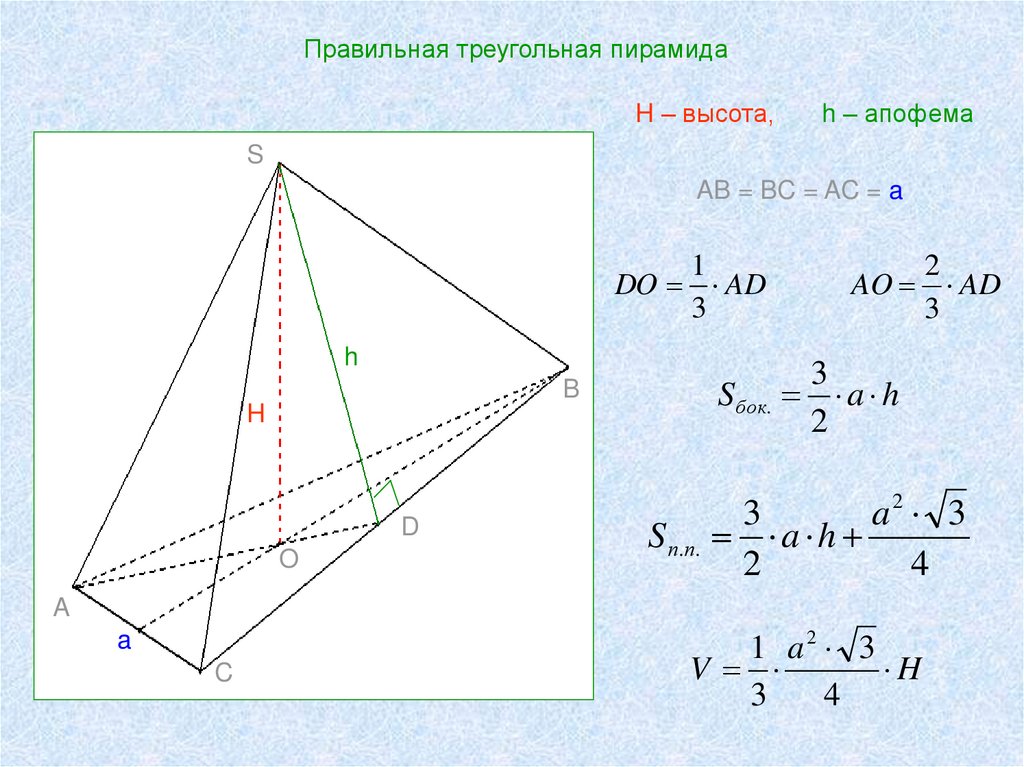
Правильная треугольная пирамида
H – высота,
h – апофема
S
AB = BC = AC = a
1
DO AD
3
h
B
H
D
O
2
AO AD
3
3
S бок. a h
2
3
a2 3
S п. п. a h
2
4
A
a
C
1 a2 3
V
H
3
4

12.

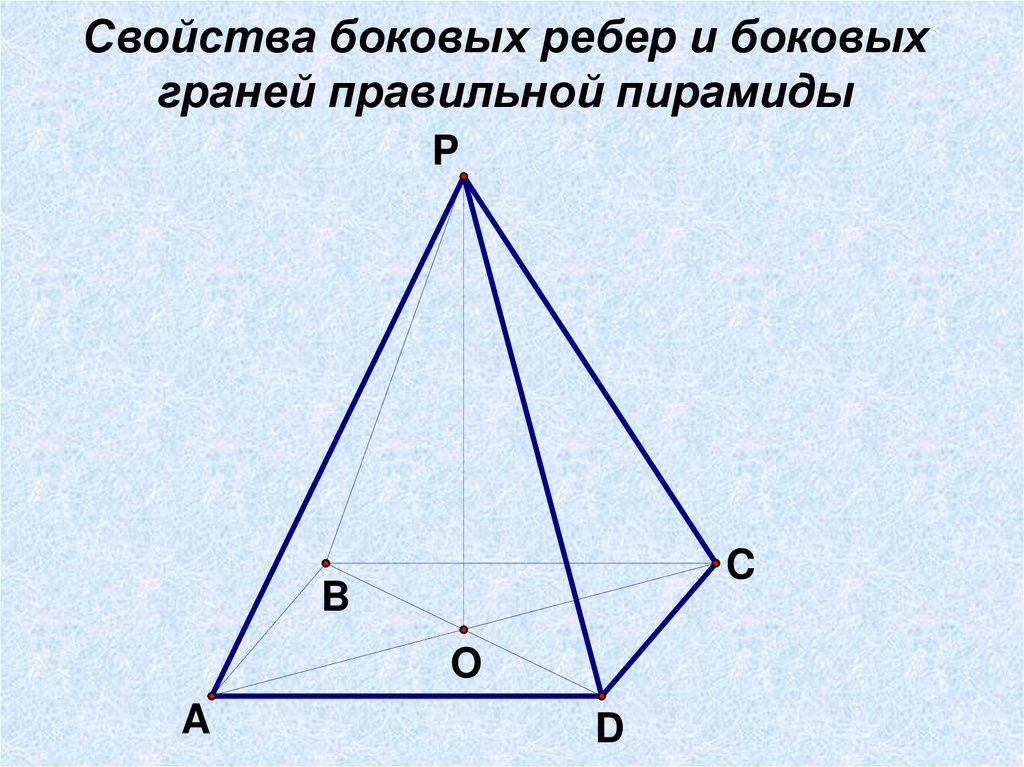
Свойства боковых ребер и боковых
граней правильной пирамиды
P
C
B
O
A
D

13.

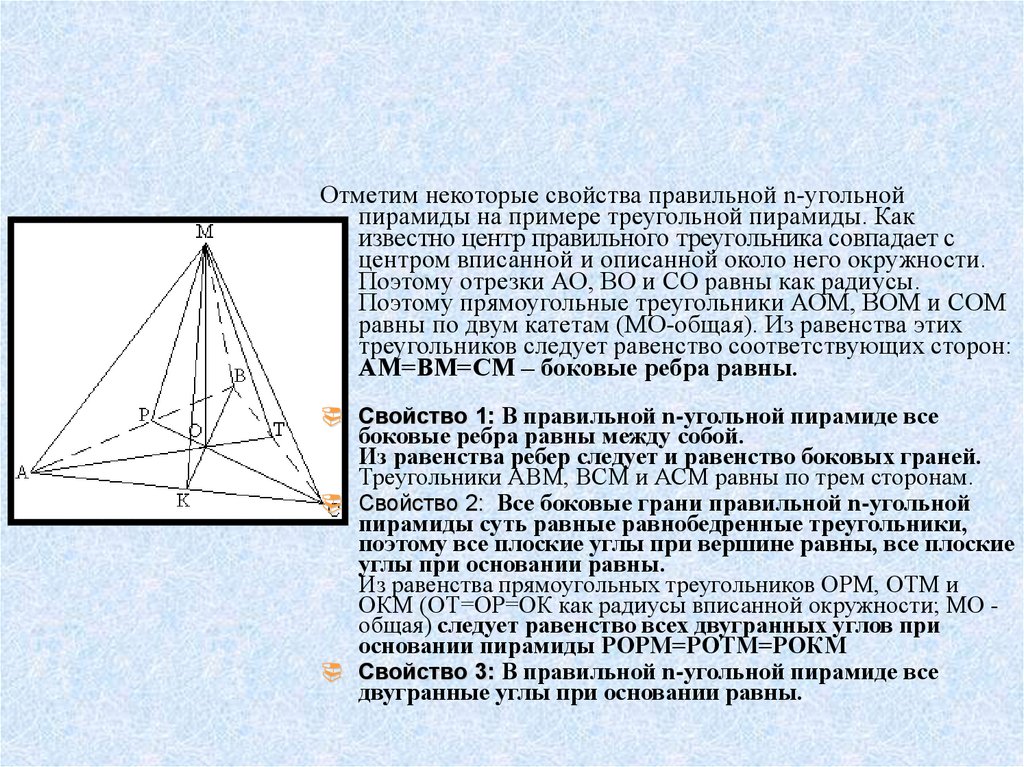
Отметим некоторые свойства правильной n-угольной
пирамиды на примере треугольной пирамиды. Как
известно центр правильного треугольника совпадает с
центром вписанной и описанной около него окружности.
Поэтому отрезки АО, ВО и СО равны как радиусы.
Поэтому прямоугольные треугольники АОМ, ВОМ и СОМ
равны по двум катетам (МО-общая). Из равенства этих
треугольников следует равенство соответствующих сторон:
АМ=ВМ=СМ – боковые ребра равны.
Свойство 1: В правильной n-угольной пирамиде все
боковые ребра равны между собой.
Из равенства ребер следует и равенство боковых граней.
Треугольники АВМ, ВСМ и АСМ равны по трем сторонам.
Свойство 2: Все боковые грани правильной n-угольной
пирамиды суть равные равнобедренные треугольники,
поэтому все плоские углы при вершине равны, все плоские
углы при основании равны.
Из равенства прямоугольных треугольников ОРМ, ОТМ и
ОКМ (ОТ=ОР=ОК как радиусы вписанной окружности; МО общая) следует равенство всех двугранных углов при
основании пирамиды РОРМ=РОТМ=РОКМ
Свойство 3: В правильной n-угольной пирамиде все
двугранные углы при основании равны.

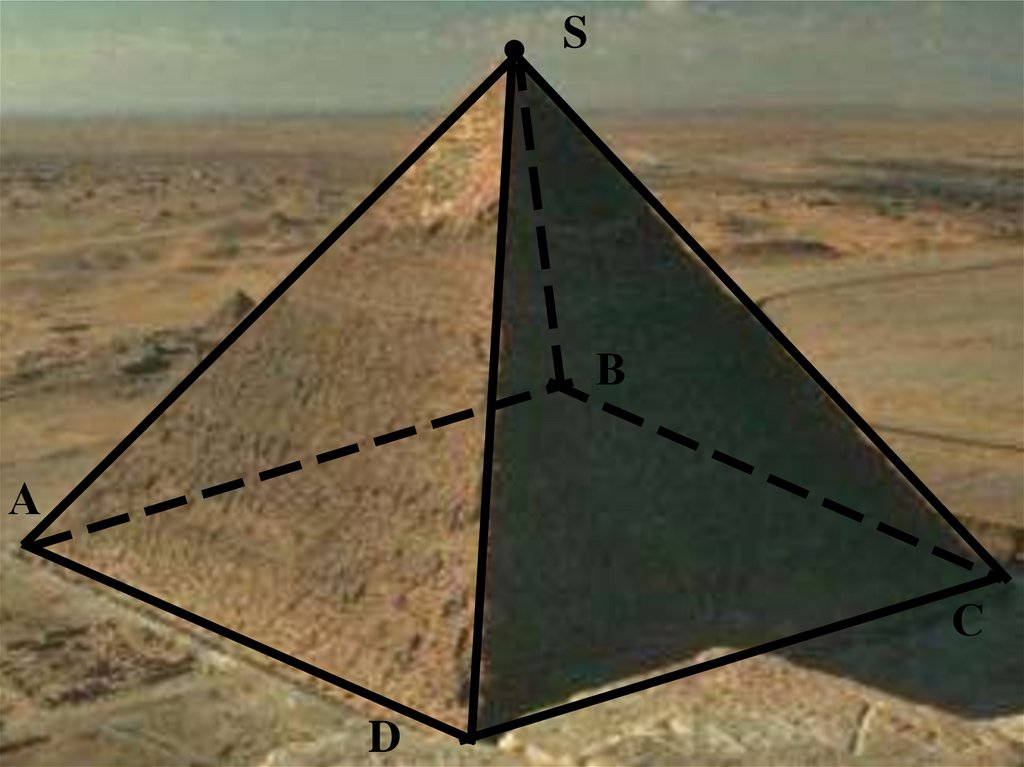
14.

S
В
А
С
D

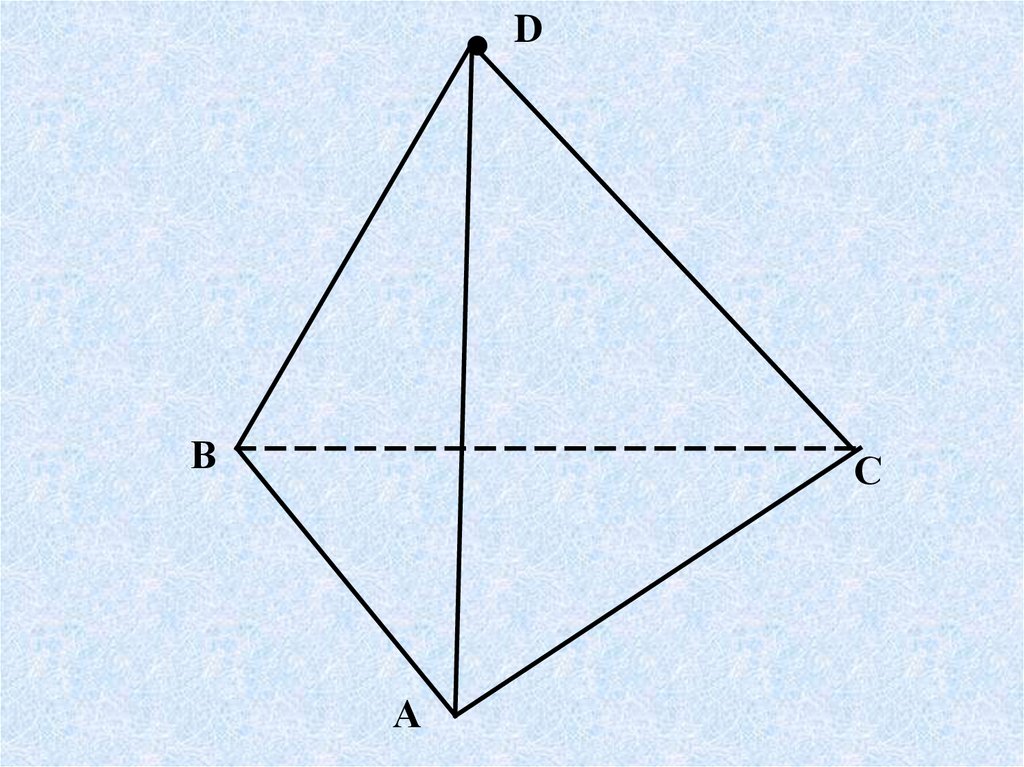
15.

В
D
С
А

16.

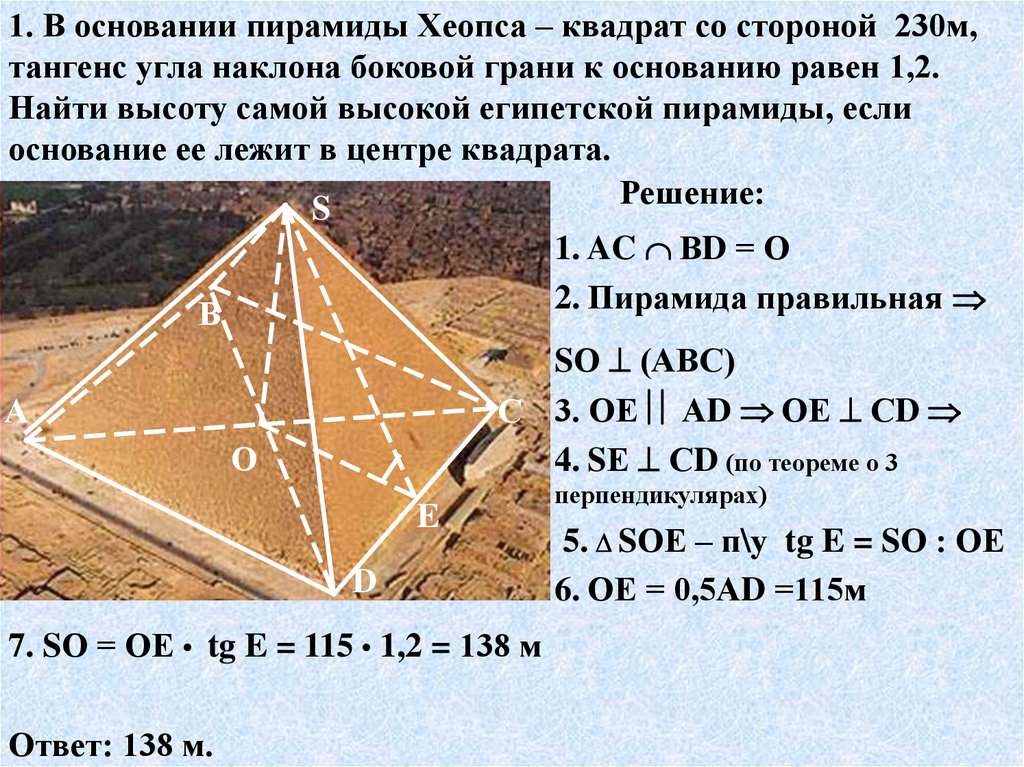
1. В основании пирамиды Хеопса – квадрат со стороной 230м,
тангенс угла наклона боковой грани к основанию равен 1,2.
Найти высоту самой высокой египетской пирамиды, если
основание ее лежит в центре квадрата.
Решение:
S
1. AC ВD = О
2. Пирамида правильная
В
SО (АВС)
С 3. ОЕ АD ОЕ СD
4. SЕ СD (по теореме о 3
А
О
E
D
7. SО = ОЕ • tg E = 115 • 1,2 = 138 м
Ответ: 138 м.
перпендикулярах)
5. SОЕ – п\у tg E = SО : ОЕ
6. ОЕ = 0,5АD =115м

17.

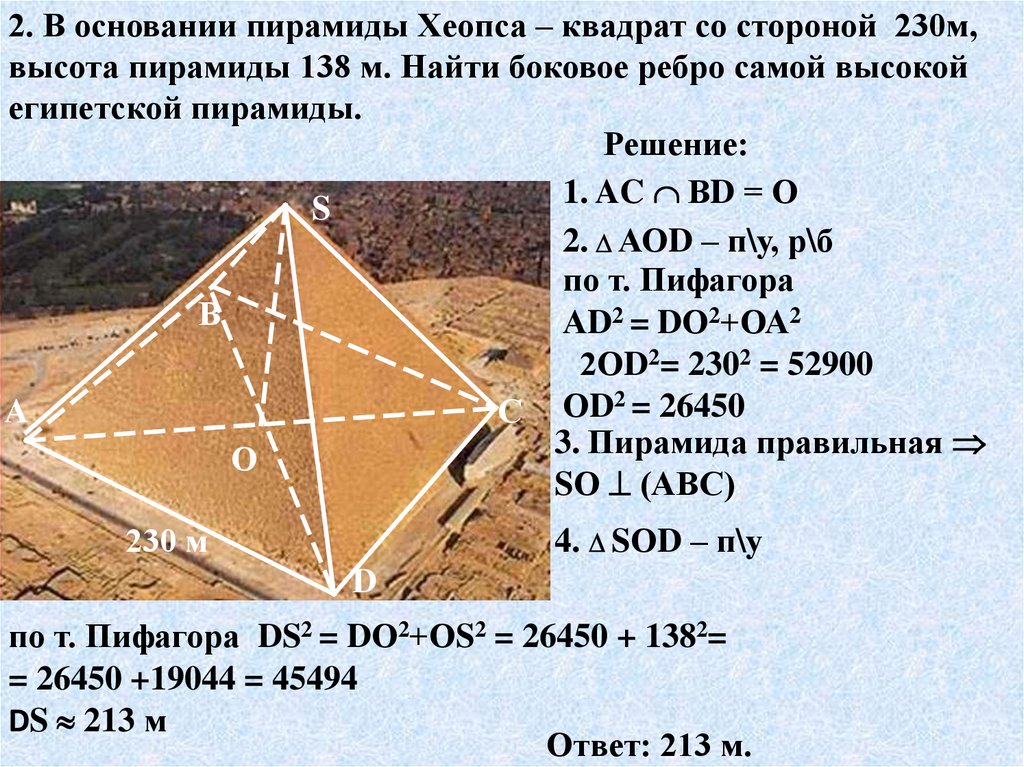
2. В основании пирамиды Хеопса – квадрат со стороной 230м,
высота пирамиды 138 м. Найти боковое ребро самой высокой
египетской пирамиды.
Решение:
1. AC ВD = О
S
2. АОD – п\у, р\б
по т. Пифагора
В
АD2 = DО2+ОА2
2ОD2= 2302 = 52900
А
С ОD2 = 26450
3. Пирамида правильная
О
SО (АВС)
230 м
4. SОD – п\у
D
по т. Пифагора DS2 = DО2+ОS2 = 26450 + 1382=
= 26450 +19044 = 45494
DS 213 м
Ответ: 213 м.

18.

19.

3.Чему равна площадь поверхности правильного
тетраэдра с ребром 1?
Решение
S
SABC – тетраэдр
1. Sпов=4Sтр
2. Sтр = 0,5а2sin600
3. Sпов=4 • 0,5а2sin600 =
=
B
A
Ответ:
C

20.

4. Найдите площадь боковой поверхности пирамиды
Хеопса, сторона основания которой равна 230 м и
высота 138 м.
Решение:
S
В
А
С
О
E
D
1. Sб.пов=4Sтр
2. AC ВD = О
3. Пирамида правильная
SО (АВС)
4. ОЕ СD ОЕ АD
5. SЕ АD (по теореме о 3
перпендикулярах)
6. SОЕ – п\у
по т. Пифагора
ЕS2 = ЕО2+ОS2 = 1152 + 1382 =
= 13225 +19044 = 32269
ЕS 180
7. ES - высота АSD
SАSD = 0,5 ЕS•АD = 0,5 •180 • 230 =20700 м2
8. Sб.пов=4Sтр = 4 • 20700 = 82800 м2
Ответ: 82800 м2

21.

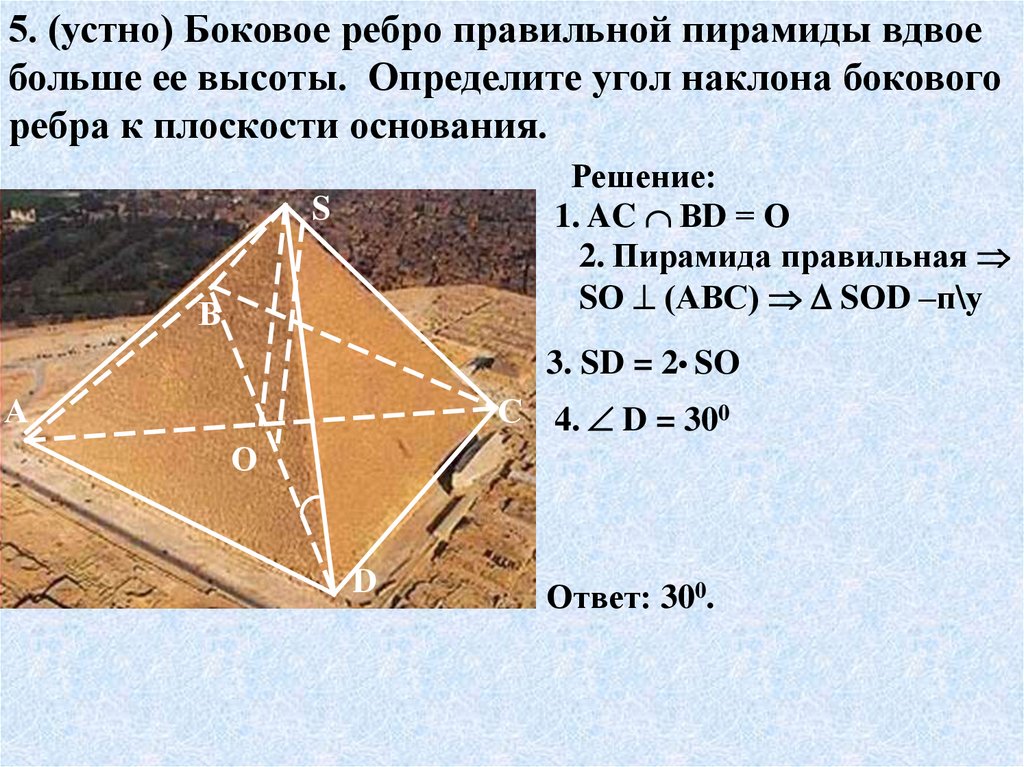
5. (устно) Боковое ребро правильной пирамиды вдвое
больше ее высоты. Определите угол наклона бокового
ребра к плоскости основания.
Решение:
1. AC ВD = О
2. Пирамида правильная
SО (АВС) SОD –п\у
S
В
3. SD = 2• SO
А
С 4. D = 300
О
D
Ответ: 300.

22.

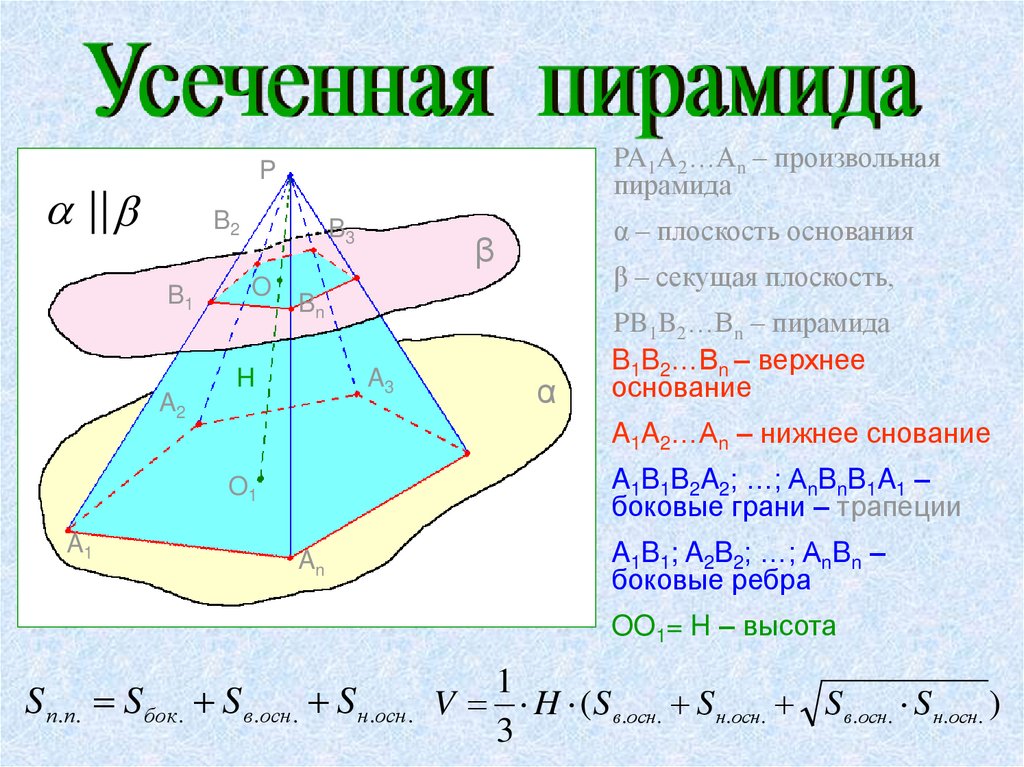
PA1A2…An – произвольная
пирамида
P
||
B2
B1
B3
O
β
β – секущая плоскость,
Bn
H
A3
A2
α
PB1B2…Bn – пирамида
B1B2…Bn – верхнее
основание
A1A2…An – нижнее снование
A1B1B2A2; …; AnBnB1A1 –
боковые грани – трапеции
O1
A1
α – плоскость основания
An
A1B1; A2B2; …; AnBn –
боковые ребра
OO1= H – высота
1
S п.п. S бок . S в.осн . S н.осн . V H (Sв.осн. Sн.осн. Sв.осн. Sн.осн. )
3

23.

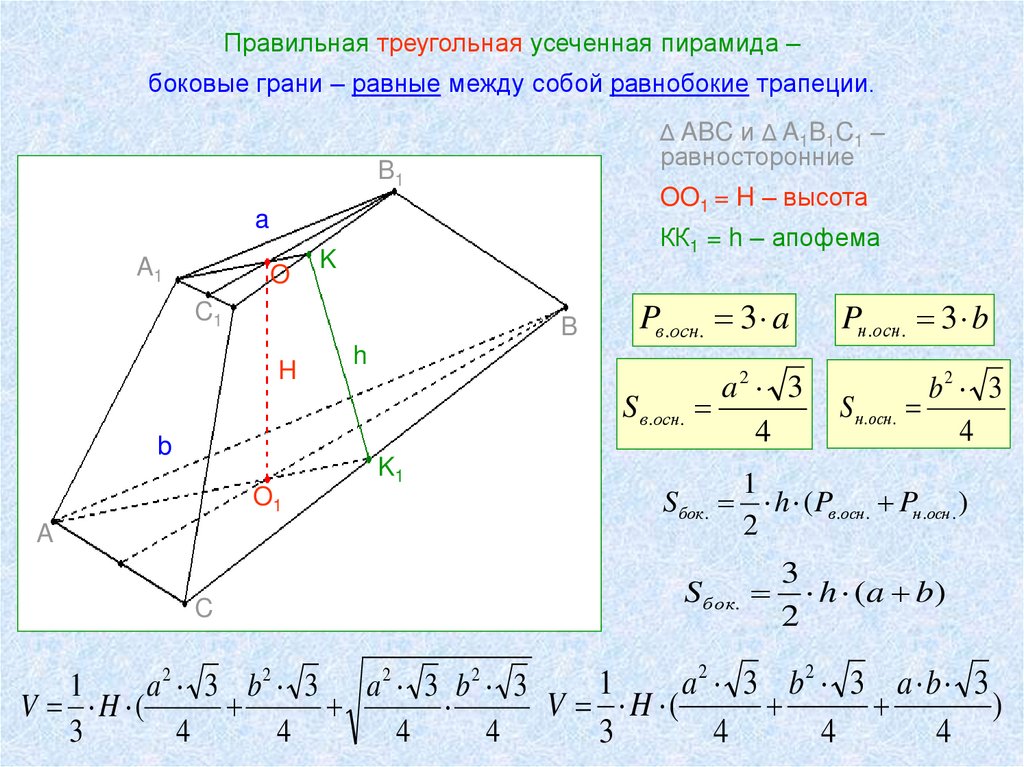
Правильная треугольная усеченная пирамида –
боковые грани – равные между собой равнобокие трапеции.
Δ ABC и Δ A1B1C1 –
равносторонние
B1
OO1 = H – высота
a
A1
O
КК1 = h – апофема
K
C1
B
H
b
h
K1
O1
A
C
Pв.осн. 3 a
Pн.осн. 3 b
a2 3
S в.осн.
4
b2 3
S н.осн.
4
1
Sбок. h ( Pв.осн. Pн.осн. )
2
S бок.
3
h ( a b)
2
1
a 3 b 3 a b 3
1
a 2 3 b2 3 a 2 3 b2 3
V H (
)
V H (
3
4
4
4
4
3
4
4
4
2
2

24.

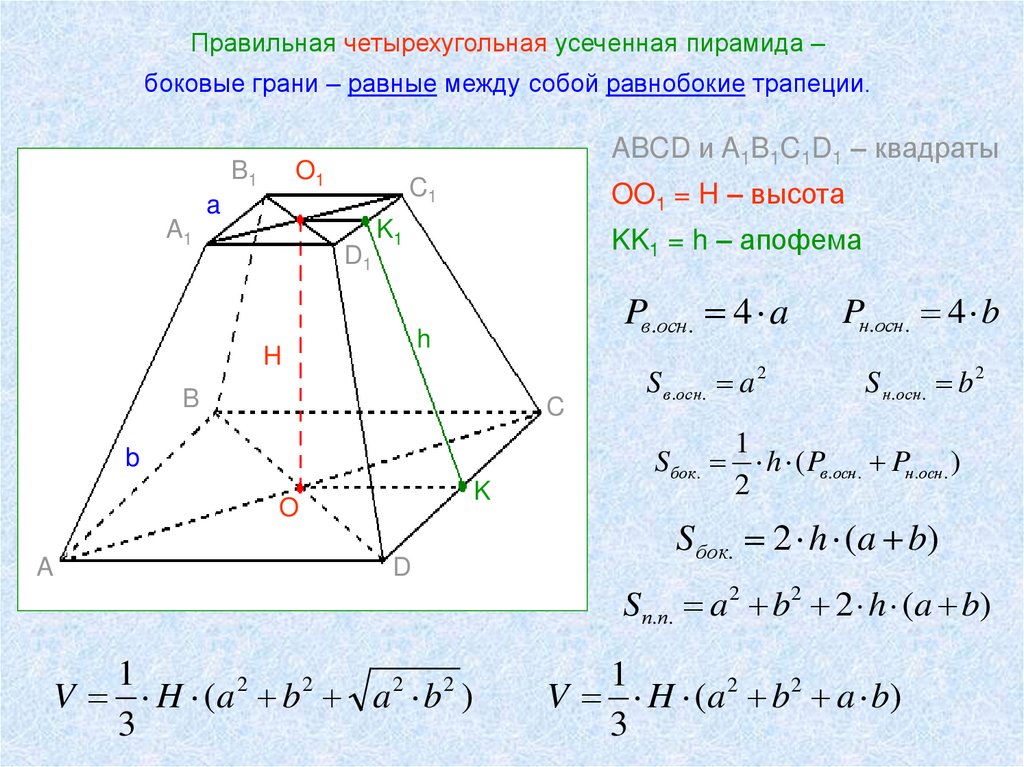
Правильная четырехугольная усеченная пирамида –
боковые грани – равные между собой равнобокие трапеции.
B1
ABCD и A1B1C1D1 – квадраты
O1
A1
OO1 = H – высота
C1
a
D1
K1
KK1 = h – апофема
h
H
B
C
b
K
O
A
D
1
V H (a 2 b 2 a 2 b 2 )
3
Pв.осн. 4 a
Pн.осн. 4 b
S в.осн. a 2
S н.осн. b 2
1
Sбок. h ( Pв.осн. Pн.осн. )
2
Sбок. 2 h (a b)
Sп.п. a 2 b2 2 h (a b)
1
V H (a 2 b 2 a b)
3

25.

Домашнее задание
• 1). Если в правильной треугольной пирамиде высота
H равна стороне основания a, то боковые ребра
составляют с плоскостью основания углы в 600.
Верно ли это утверждение?
• 2). Сторона квадрата равна 10 см. Доказать, что
нельзя, используя его в качестве основания,
построить правильную четырехугольную пирамиду
с боковым ребром 7 см.
• 3). Доказать или опровергнуть утверждение: «если в
пирамиде все ребра равны, то пирамида
правильная».