Similar presentations:
Многогранник - геометрическое тело
1.
2.
3.
Многогранник - геометрическое тело,ограниченное плоскими многоугольниками.
Плоские многоугольники
называются гранями многогранника
стороны многоугольника –
ребрами многогранника
вершины многоугольника –
вершинами многогранника.
С
4.
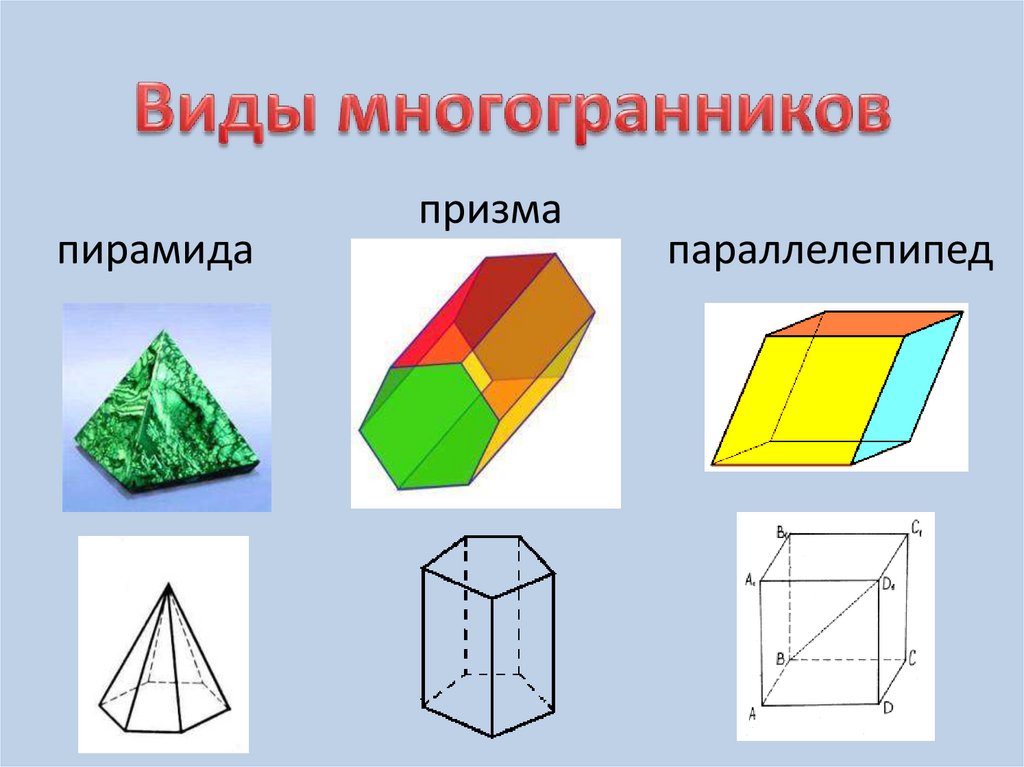
пирамидапризма
параллелепипед
5.
Основаниемявляется
многоугольник
боковые грани –
треугольники
(n-угольная пирамида имеет n+1
граней)
Пирамида называется
правильной,
если в основании лежит
правильный
многоугольник, а вершина
проектируется
в центр основания
6.
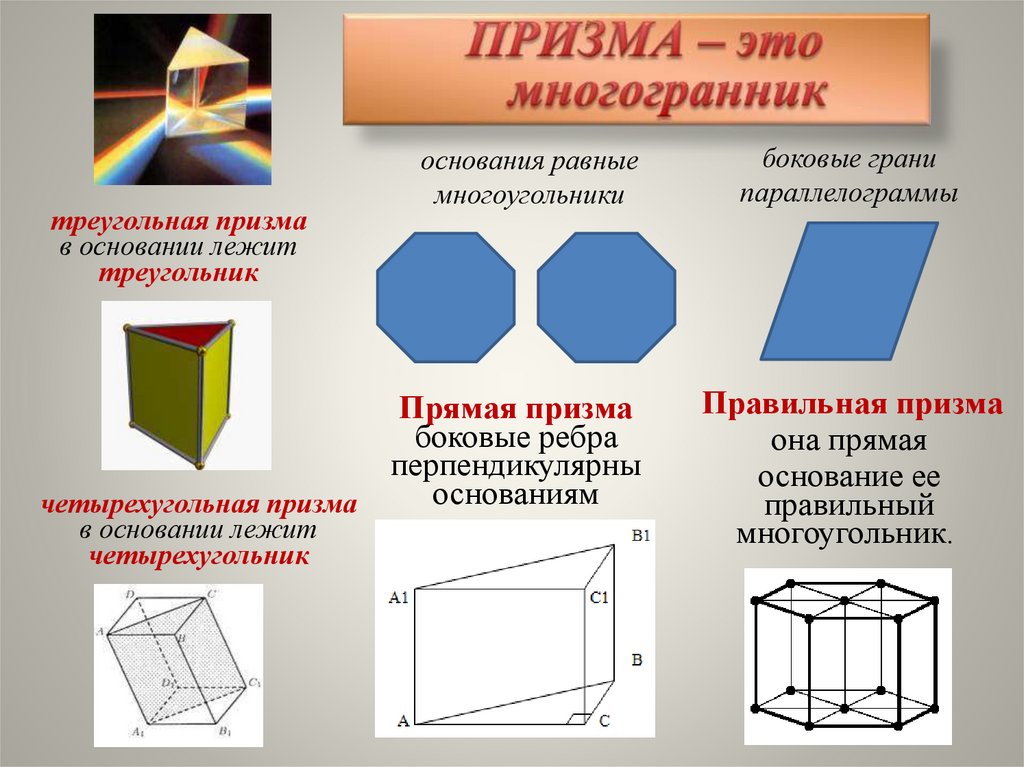
треугольная призмав основании лежит
треугольник
четырехугольная призма
в основании лежит
четырехугольник
основания равные
многоугольники
боковые грани
параллелограммы
Прямая призма
боковые ребра
перпендикулярны
основаниям
Правильная призма
она прямая
основание ее
правильный
многоугольник.
7.
основанием которойявляется параллелограмм
Параллелепипед, основанием которого является
прямоугольник или квадрат называется прямым
Свойства параллелепипеда:
1. Противоположные грани параллелепипеда параллельны и равны.
2. Диагонали параллелепипеда пересекаются в одной точке и
делятся этой точкой пополам.
8.
( от ,,тетра”- четыре и греческого ,,hedra” - грань)состоит из 4-х правильных треугольников, в
каждой его вершине сходятся 3 ребра.
Тетраэдр символизировал огонь,
т.к. его вершина устремлена вверх
9.
( от греческого ,,гекса” - шесть и ,,hedra” - грань)имеет 6 квадратных граней, в каждой его вершине
сходятся 3 ребра.
Гексаэдр больше известен как куб (от латинского
,,cubus”; от греческого ,,kubos”.
Гексаэдр (куб) символизировал землю,
так как самый «устойчивый»
10.
(от греческого okto - восемь и hedra - грань)имеет 8 граней (треугольных),
в каждой вершине сходятся 4 ребра.
Октаэдр символизировал воздух,
как самый "воздушный"
11.
(от греческого eikosi - двадцать и hedra - грань)имеет 20 граней (треугольных),
в каждой вершине сходится 5 рёбер
Икосаэдр символизировал воду,
так как он самый «обтекаемый»
12.
(от греческого dodeka - двенадцать и hedra - грань)имеет 12 граней (пятиугольных),
в каждой вершине сходятся 3 ребра.
Додекаэдр воплощал в себе "все сущее",
символизировал все мироздание, считался
главным
13.
14.
Название ТетраэдрФорма
граней
Число
граней
Число
ребер
Число
вершин
Куб
Октаэдр
Додекаэдр
Икосаэдр
15.
Математика - гимнастика для ума,СТЕРЕОМЕТРИЯ - витамин для мозга.
16.
Многогранники в искусствеВ эпоху Возрождения большой интерес к
формам правильных многогранников
проявили скульпторы. архитекторы,
художники. Леонардо да Винчи (1452 1519) например, увлекался теорией
многогранников и часто изображал их на
своих полотнах. Он проиллюстрировал
правильными и полуправильными
многогранниками книгу Монаха Луки
Пачоли ''О божественной пропорции.''
Знаменитый художник, увлекавшийся
геометрией Альбрехт Дюрер (14711528) , в известной гравюре
''Меланхолия '‘ на переднем плане
изобразил додекаэдр.
художник Эшер
17.
18.
Великаяпирамида в Гизе
Галикарнасский
мавзолей
Мечеть
Кул-Шариф
Никольский собор
Башня Сююмбике
Александрийский
маяк
19.
Кристаллы белого фосфора образованы молекулами Р4 .Такая молекула имеет вид тетраэдра.
Молекулы зеркальных изомеров молочной кислоты
также являются тетраэдрами.
Кристаллическая решётка метана имеет форму тетраэдра.
Метан горит бесцветным пламенем.
С воздухом образует взрывоопасные смеси.
Используется как топливо.
Сфалерит - сульфид цинка (ZnS).
Кристаллы этого минерала имеют форму тетраэдров, реже – ромбододекаэдров.
20.
Форму октаэдра имеет монокристалл алюмокалиевых кварцев,формула которого K(AL(SO4)2) * 12H2O.
Они применяются для протравливания тканей, выделки кожи.
Одним из состояний полимерной молекулы углерода, наряду с графитом,
является алмаз Алмазы обычно имеют октаэдр в качестве формы огранки.
Алмаз (от греческого adamas – несокрушимый) – бесцветный или окрашенный
кристалл с сильным блеском в виде октаэдра.
Кристаллы алмаза представляют собой гигантские полимерные молекулы и
обычно имеют форму огранки октаэдра, ромбододекаэдра, реже — куба или
тетраэдра.
21.
||АВСD и A1B1C1D1 – равные
параллелограммы – основания
АА1|| ВВ1|| СС1|| DD1 – боковые
ребра
В1
С1
А1
D1
Все грани параллелограммы.
AA1B1B; BB1C1C; CC1D1D; AA1D1D –
боковые грани
DB1 – диагональ
Свойства.
В
А
С
D
1. Противолежащие грани
параллелепипеда параллельны и
равны.
2. Диагонали параллелепипеда
пересекаются в одной точке и точкой
пересечения делятся пополам.
22.
– это параллелепипед, у которого боковые грани являютсяпрямоугольниками.
B1
С1
A1
D1
c
Lкаркаса 4 (a b c)
Sбок 2 (ac bc)
S п.п. Sбок. 2Sосн.
В
А
С
a
D
b
V Sосн. c
23.
– это параллелепипед, у которого все грани прямоугольники.a – длина, b – ширина,
с – высота, d – диагональ
c
d
d2 = a2 + b2 + c2
S п.п. 2 (ab bc ac)
а
b
V a b c
24.
: основания – равные n – угольники,лежащие в параллельных плоскостях,
боковые грани – параллелограммы.
Наклонная – боковые грани – параллелограммы.
HH1 – высота призмы
AH (k) – боковое ребро призмы
H
k
M
N
P
F
D
A
FMNPD – сечение,
перпендикулярное боковому ребру
H1
Sбок. Pсеч. k
S п.п. Sбок. 2Sосн.
V Sсеч. k
25.
Прямая призма – боковые грани – прямоугольники.все грани - квадраты
V a
а
d
3
H
а
а
d 3 a
2
V Sосн. H
Lкаркаса 12 a
Sбок. Pосн. H
S п.п. 6 a
2
2
26.
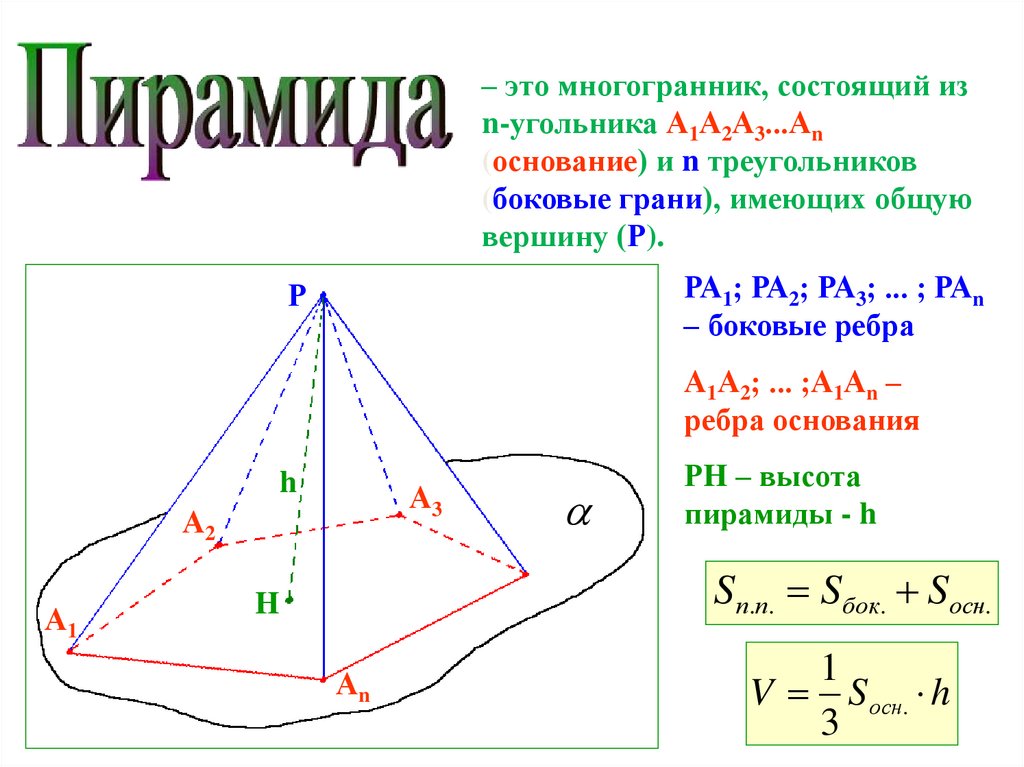
– это многогранник, состоящий изn-угольника А1А2А3...Аn
(основание) и n треугольников
(боковые грани), имеющих общую
вершину (Р).
РА1; РА2; РА3; ... ; РАn
– боковые ребра
Р
А1А2; ... ;А1Аn –
ребра основания
h
А3
А2
А1
РH – высота
пирамиды - h
S п.п. Sбок. Sосн.
H
Аn
1
V S осн. h
3
27.
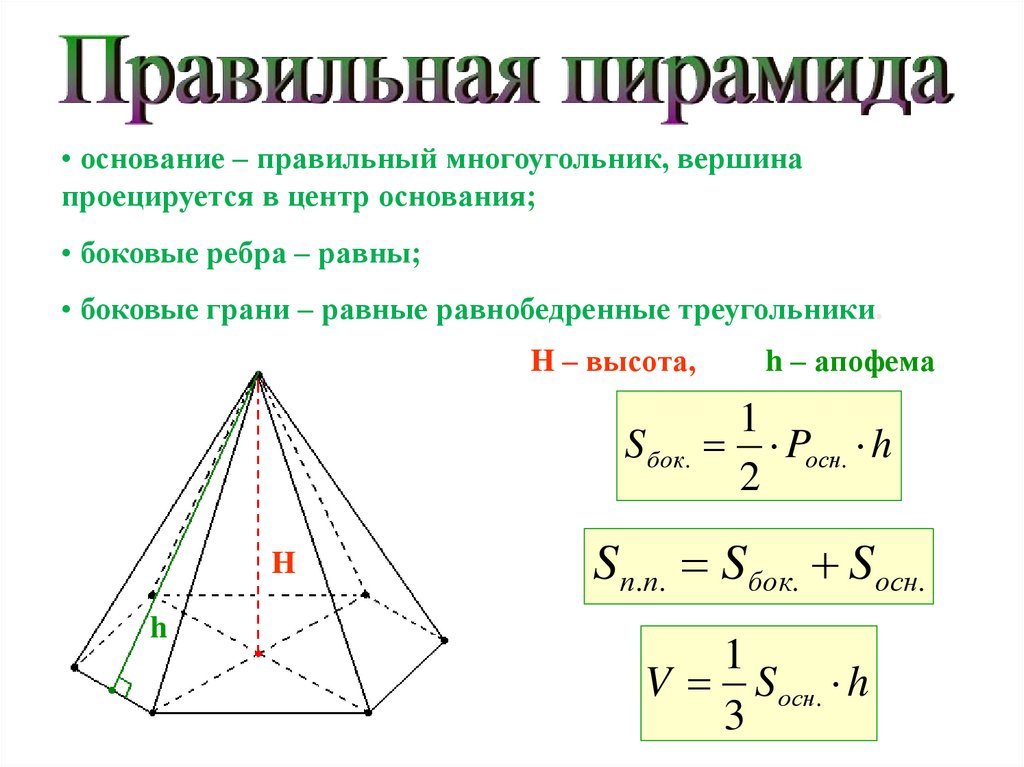
• основание – правильный многоугольник, вершинапроецируется в центр основания;
• боковые ребра – равны;
• боковые грани – равные равнобедренные треугольники.
H – высота,
h – апофема
1
S бок. Pосн. h
2
H
h
S п.п. Sбок. Sосн.
1
V S осн. h
3
28.
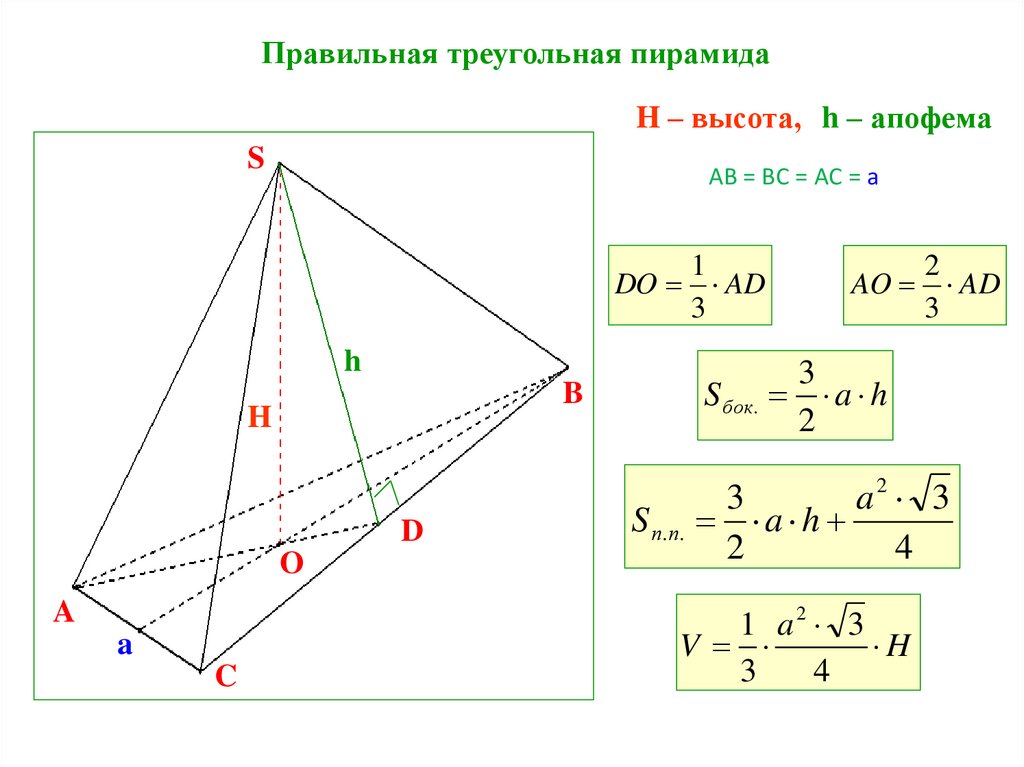
Правильная треугольная пирамидаH – высота, h – апофема
S
AB = BC = AC = a
1
DO AD
3
h
B
H
D
O
A
a
C
AO
2
AD
3
3
S бок. a h
2
3
a2 3
S п.п. a h
2
4
1 a2 3
V
H
3
4
29.
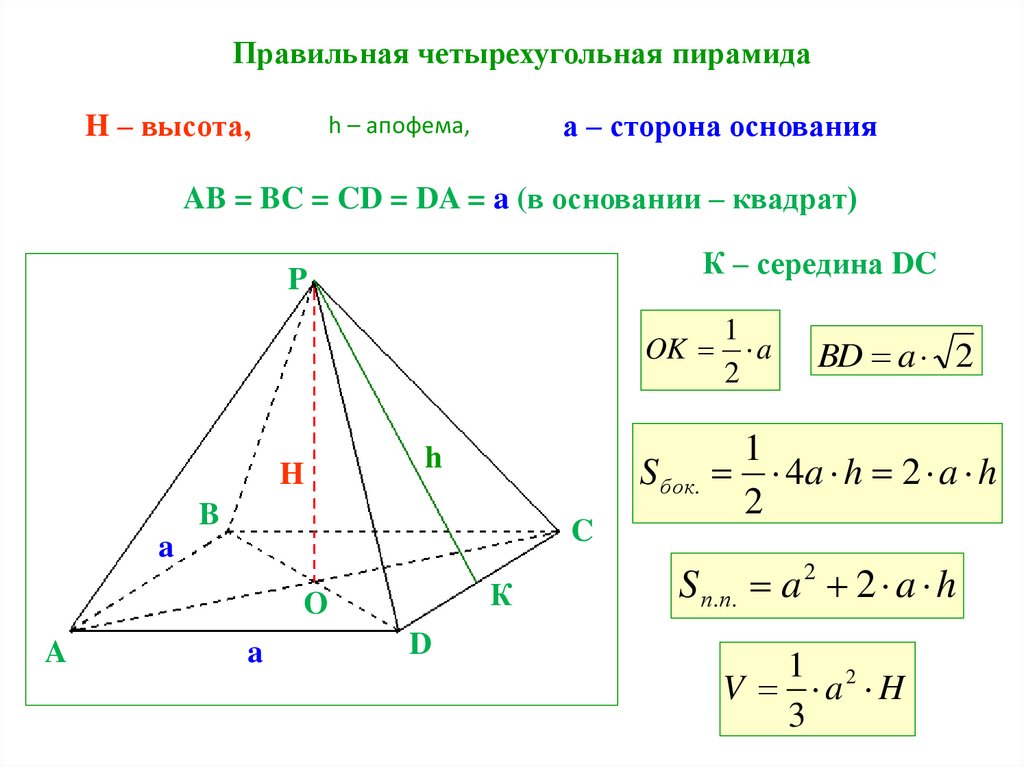
Правильная четырехугольная пирамидаH – высота,
а – сторона основания
h – апофема,
AB = BC = CD = DA = a (в основании – квадрат)
К – середина DC
P
1
OK a
2
H
h
B
C
a
К
O
A
a
D
BD a 2
1
S бок. 4a h 2 a h
2
S п.п. a 2 2 a h
1 2
V a H
3
30.
||B1
A2
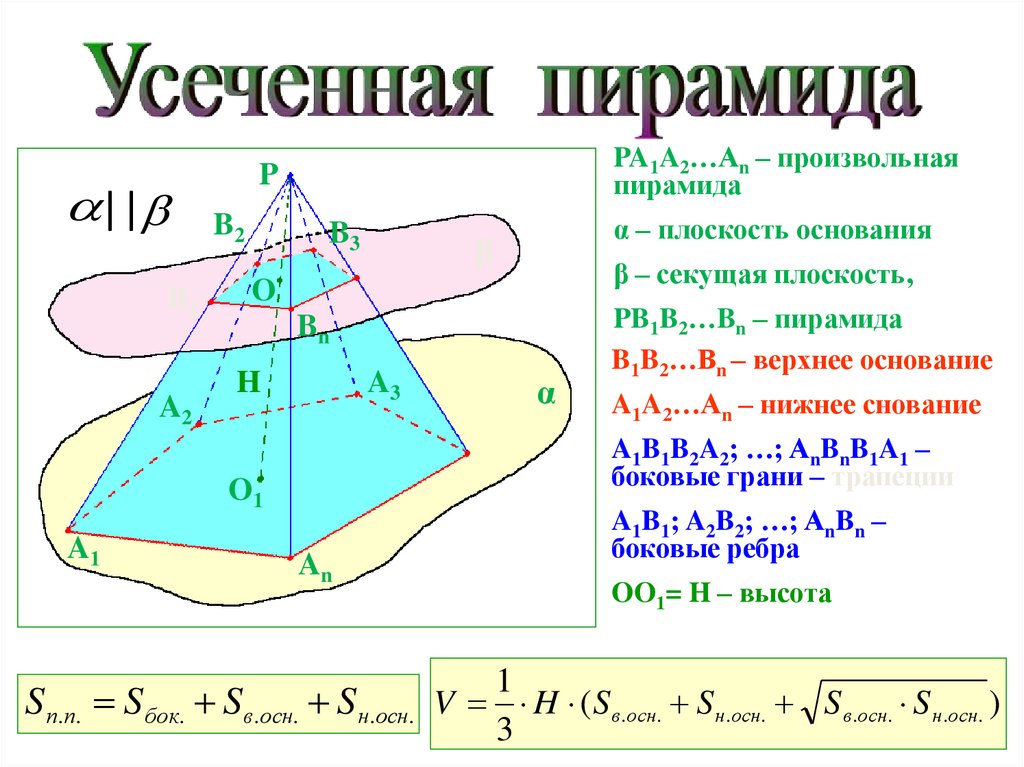
PA1A2…An – произвольная
пирамида
P
B2
B3
β
β – секущая плоскость,
O
Bn
H
A3
α
PB1B2…Bn – пирамида
B1B2…Bn – верхнее основание
A1A2…An – нижнее снование
A1B1B2A2; …; AnBnB1A1 –
боковые грани – трапеции
O1
A1
α – плоскость основания
An
A1B1; A2B2; …; AnBn –
боковые ребра
OO1= H – высота
1
S п.п. Sбок. Sв.осн. S н.осн. V H ( S в.осн. S н.осн. S в.осн. S н.осн. )
3
31.
Правильная треугольная усеченная пирамида –боковые грани – равные между собой равнобокие трапеции.
Δ ABC и Δ A1B1C1 –
равносторонние
B1
OO1 = H – высота
a
КК1 = h – апофема
O K
A1
C1
B
H
b
O1
h
K1
Pв.осн. 3 a
Pн.осн. 3 b
a2 3
S в.осн.
4
b2 3
S н.осн.
4
S бок.
A
C
1
h ( Pв.осн. Pн.осн. )
2
S бок.
3
h ( a b)
2
1
a 3 b 3 a b 3
1
a2 3 b2 3
a2 3 b2 3
V H (
)
V H (
3
4
4
4
4
3
4
4
4
2
2
32.
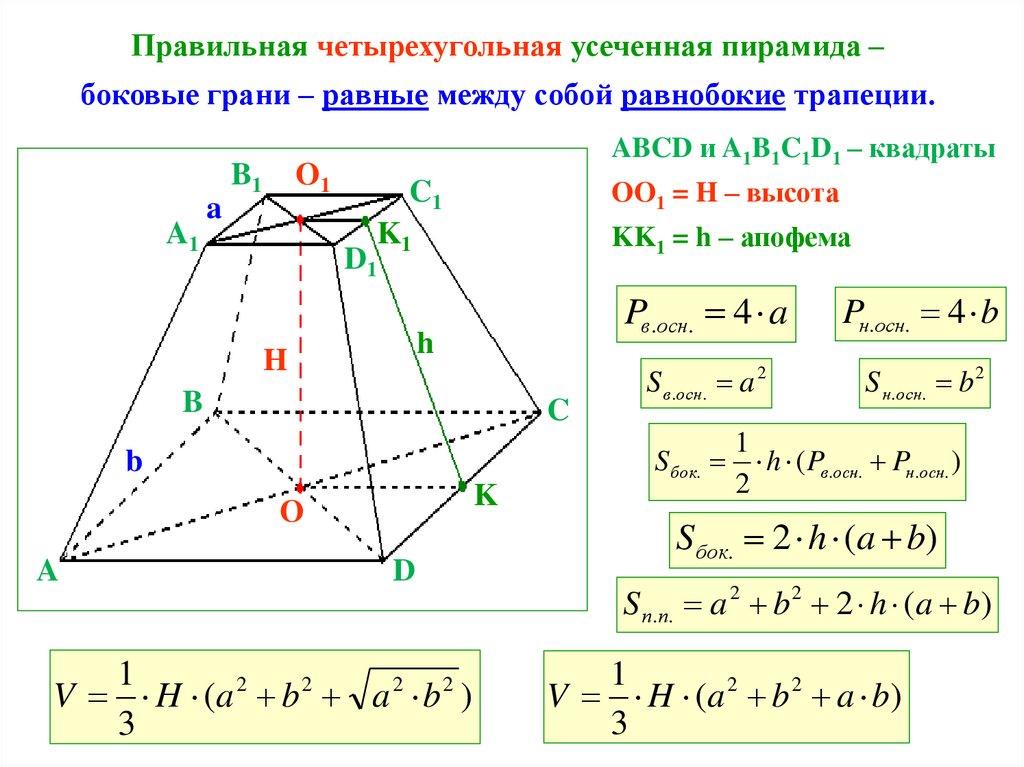
Правильная четырехугольная усеченная пирамида –боковые грани – равные между собой равнобокие трапеции.
B1
A1
ABCD и A1B1C1D1 – квадраты
O1
a
OO1 = H – высота
C1
KK1 = h – апофема
K1
D1
h
H
B
C
Pн.осн. 4 b
S в.осн. a 2
S н.осн. b 2
S бок.
b
K
O
A
Pв.осн. 4 a
D
1
V H (a 2 b 2 a 2 b 2 )
3
1
h ( Pв.осн. Pн.осн. )
2
Sбок. 2 h (a b)
S п.п. a 2 b 2 2 h ( a b)
1
V H ( a 2 b 2 a b)
3
33.
Многогранник - геометрическое тело,ограниченное со всех сторон плоскими
многоугольниками, называемыми гранями.
Стороны граней называются ребрами
многогранника, а концы ребер — вершинами
многогранника. По числу граней различают
четырехгранники, пятигранники и т. д.
























 mathematics
mathematics








