Similar presentations:
Пирамида. Правильная и усеченная пирамида
1.
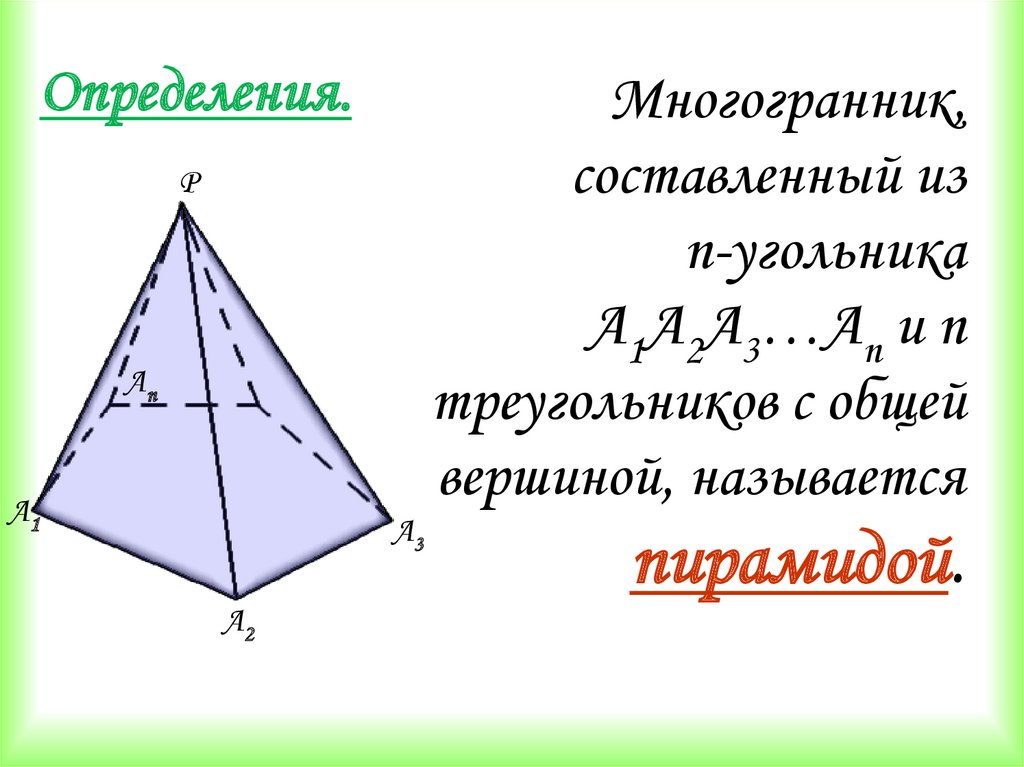
2. Определения.
Многогранник,составленный из
n-угольника
А1А2A3…Аn и n
треугольников с общей
вершиной, называется
P
Аn
A1
A3
A2
пирамидой.
3.
Пирамиду с основанием А1А2…Аn и вершиной Робозначают : РА1А2…Аn и называют n-угольной
пирамидой.
Многоугольник А1А2А3…Аn
называется основанием, а
треугольники- боковыми гранями
пирамиды.
Точка Р называется вершиной
пирамиды, а отрезки РА1,РА2,…,РАn
– ее боковыми ребрами.
4.
Перпендикуляр, проведенный из вершины пирамиды кплоскости основания, называется высотой пирамиды.
Р
М
А
Е
Н
В
РН - высота
С
РН- высота
(не лежит во внутренней области
пирамиды).
5.
Пирамида называется правильной, если ееоснование - правильный многоугольник, а
отрезок, соединяющий вершину пирамиды с
центром ее основания, является высотой
данной пирамиды.
S
1. SАВСD – правильная пирамида.
2. АВСD – квадрат (правильный
четырехугольник).
D
3. SО – высота.
А
С
О
В
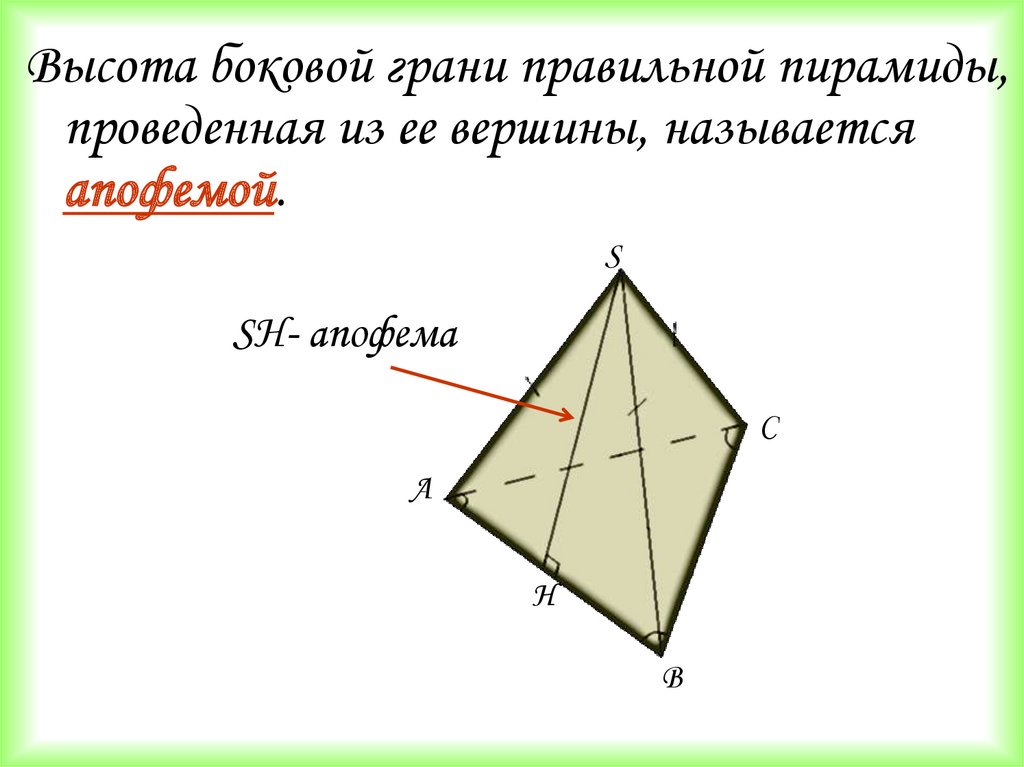
6.
Высота боковой грани правильной пирамиды,проведенная из ее вершины, называется
апофемой.
S
SH- апофема
С
А
Н
В
7.
Возьмем произвольную пирамидуPA1A2…An и проведем секущую
плоскость β||α основания пирамиды и
пересекающую боковые ребра в точках
B1,B2,…,Bn. Плоскость β разбивает
пирамиду на 2 многогранника.
Многогранник, гранями которого
являются n–угольники A1A2…An и
B1B2…Bn(нижнее и верхнее основания),
расположенные в параллельных
плоскостях, и n четырехугольников
A1A2B2B1, A2A3B3B2, …,
AnA1B1Bn(боковые грани), называется
усеченной пирамидой.
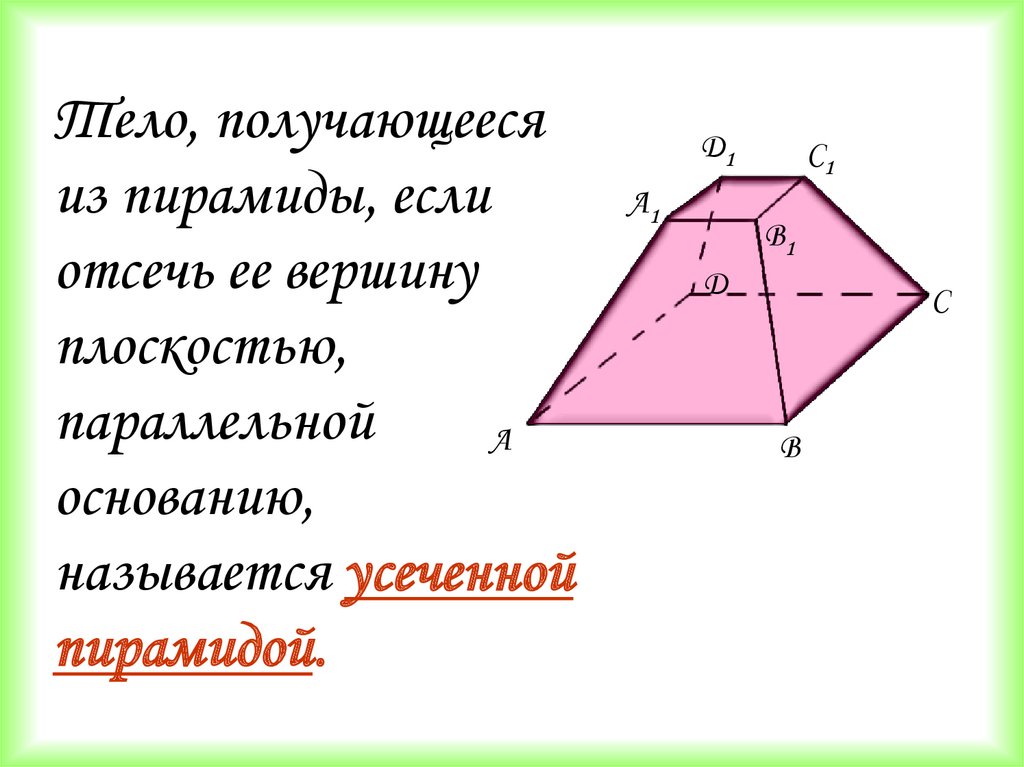
8.
Тело, получающеесяиз пирамиды, если
отсечь ее вершину
плоскостью,
параллельной
А
основанию,
называется усеченной
пирамидой.
D1
А1
С1
В1
D
С
В
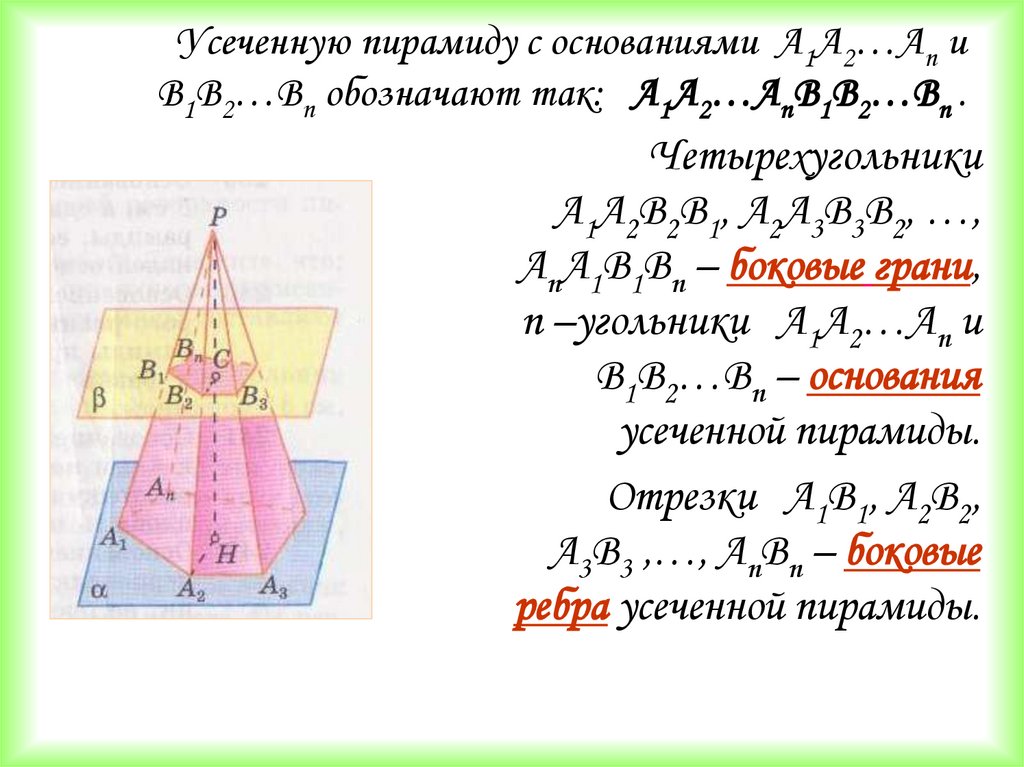
9.
Усеченную пирамиду с основаниями А1А2…Аn иВ1В2…Вn обозначают так: А1А2…АnВ1В2…Вn .
Четырехугольники
A1A2B2B1, A2A3B3B2, …,
AnA1B1Bn – боковые грани,
n –угольники А1А2…Аn и
В1В2…Вn – основания
усеченной пирамиды.
Отрезки А1В1, А2В2,
А3В3 ,…, АnВn – боковые
ребра усеченной пирамиды.
10.
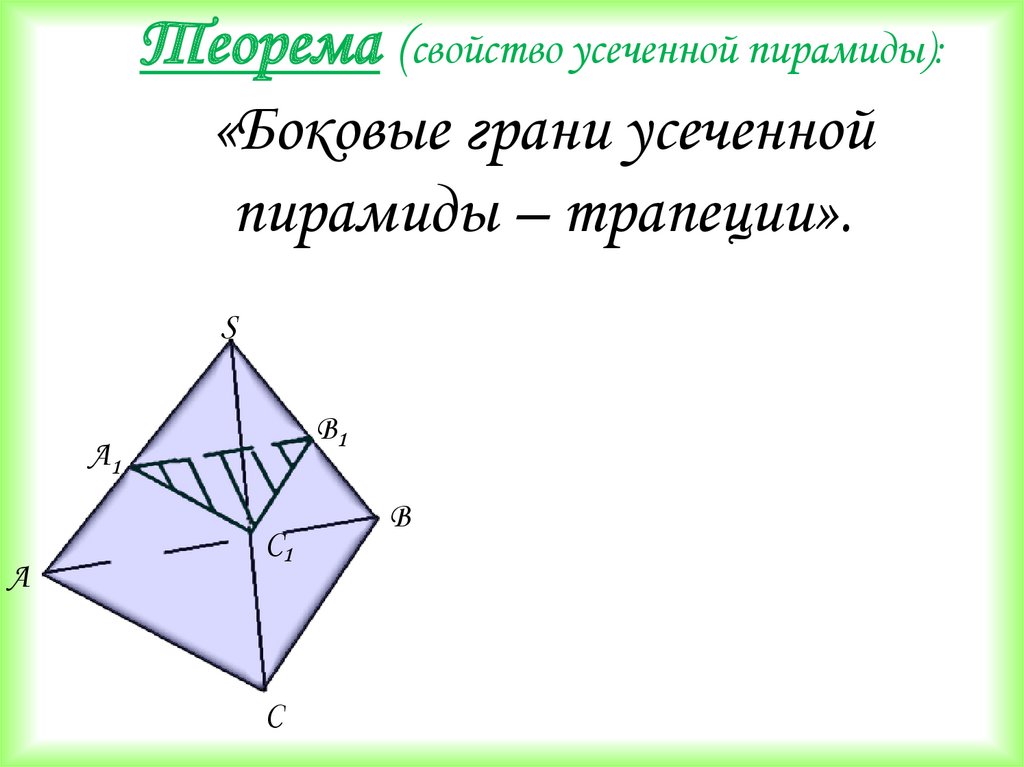
Теорема (свойство усеченной пирамиды):«Боковые грани усеченной
пирамиды – трапеции».
S
B1
А1
А
С1
С
B
11.
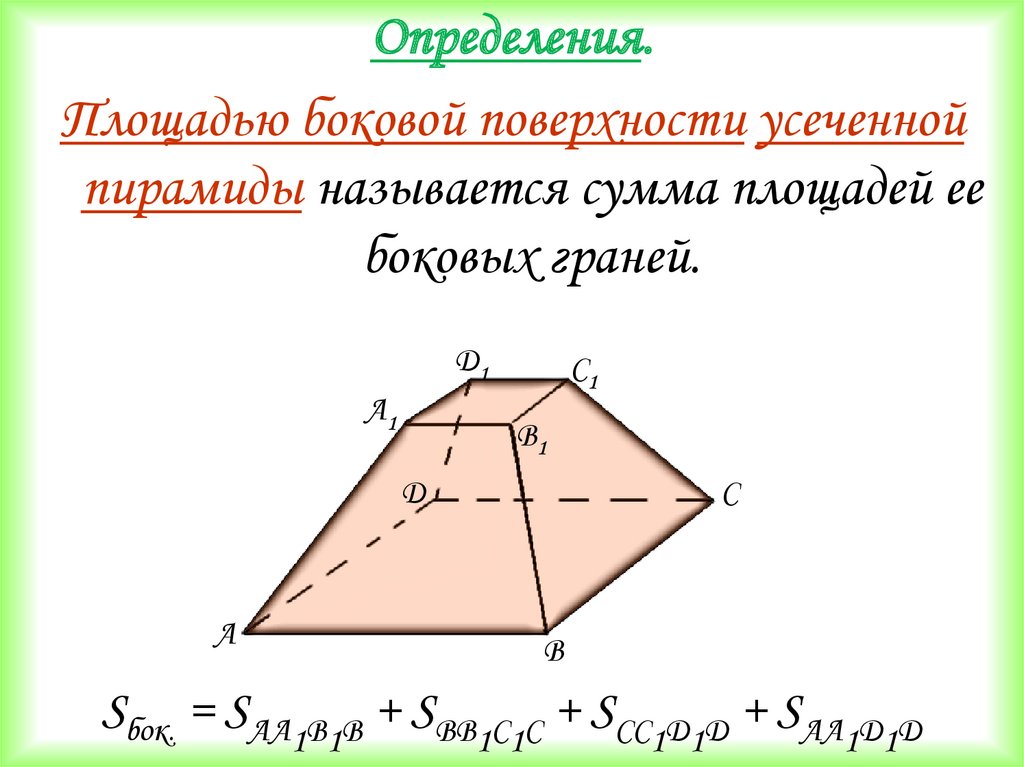
Определения.Площадью боковой поверхности усеченной
пирамиды называется сумма площадей ее
боковых граней.
D1
А1
С1
В1
D
А
С
В
Sбок. = SАА1В1В + SВВ1С1С + SСС1D1D + SАА1D1D
12.
РУсеченная пирамида
называется правильной,
если она получена сечением
правильной пирамиды
плоскостью, параллельной
плоскости основания.
М
Н
К
С
А
Основания правильной
усеченной пирамиды –
правильные
многоугольники, а боковые
грани – равнобедренные
трапеции.
В
1. (МНК) || ;
2. АСНМ,АМКВ,ВСНК –
равнобедренные трапеции, т.е.
АМ=КВ=НС
13.
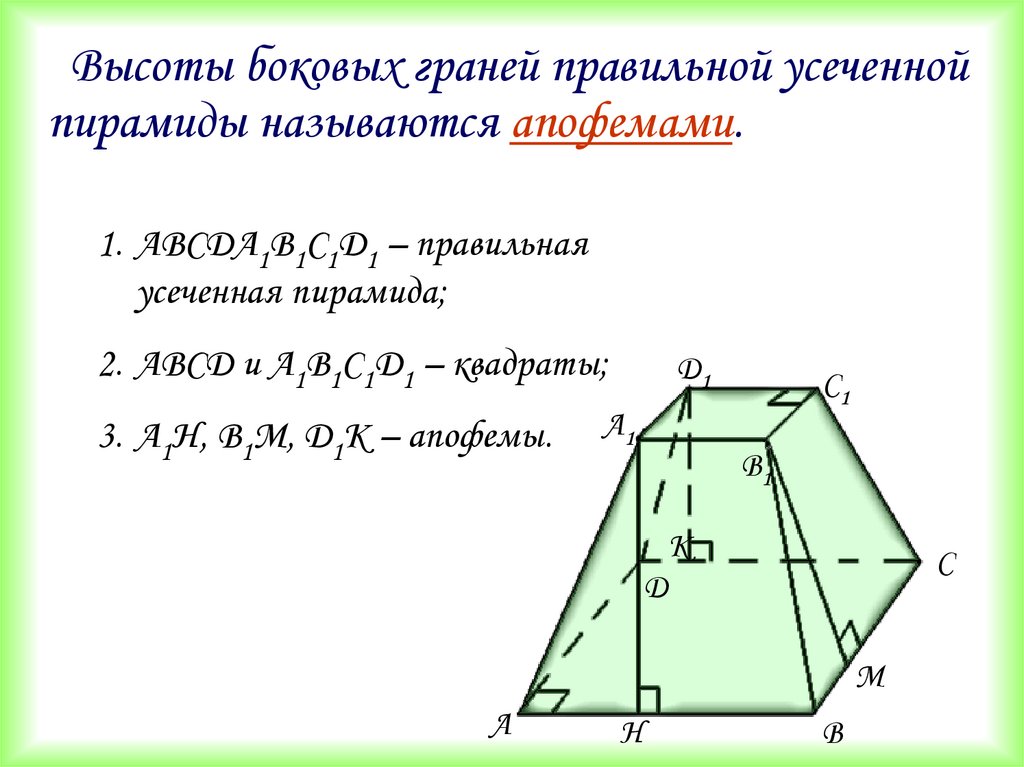
Высоты боковых граней правильной усеченнойпирамиды называются апофемами.
1. АВСDА1В1С1D1 – правильная
усеченная пирамида;
2. АВСD и А1В1С1D1 – квадраты;
3. А1Н, В1М, D1К – апофемы.
D1
А1
С1
В1
К
С
D
М
А
Н
В
14.
Теорема:«Площадь боковой поверхности
правильной усеченной пирамиды
равна произведению полусуммы
периметров оснований на апофему».
Sбок. пр. пир. =½∙(Росн +Росн ) ∙d
1
2
15. Теорема.
Объем V усеченной пирамиды, высотакоторой равна h, а площади оснований равны
S и S1, вычисляется по формуле
1
V усеч .пир . h S S 1 S S1
3








 mathematics
mathematics








