Усеченная пирамида

1. УСЕЧЕННАЯ ПИРАМИДА Учитель математики Носова Татьяна Николаевна МБОУ СОШ № 5 г.Николаевск-на-Амуре Хабаровского края 2010 год

2. План.

1. Определение усечённой
пирамиды.
2. Элементы усечённой пирамиды.
3. Вывод формулы площади
боковой поверхности
правильной усечённой
пирамиды.

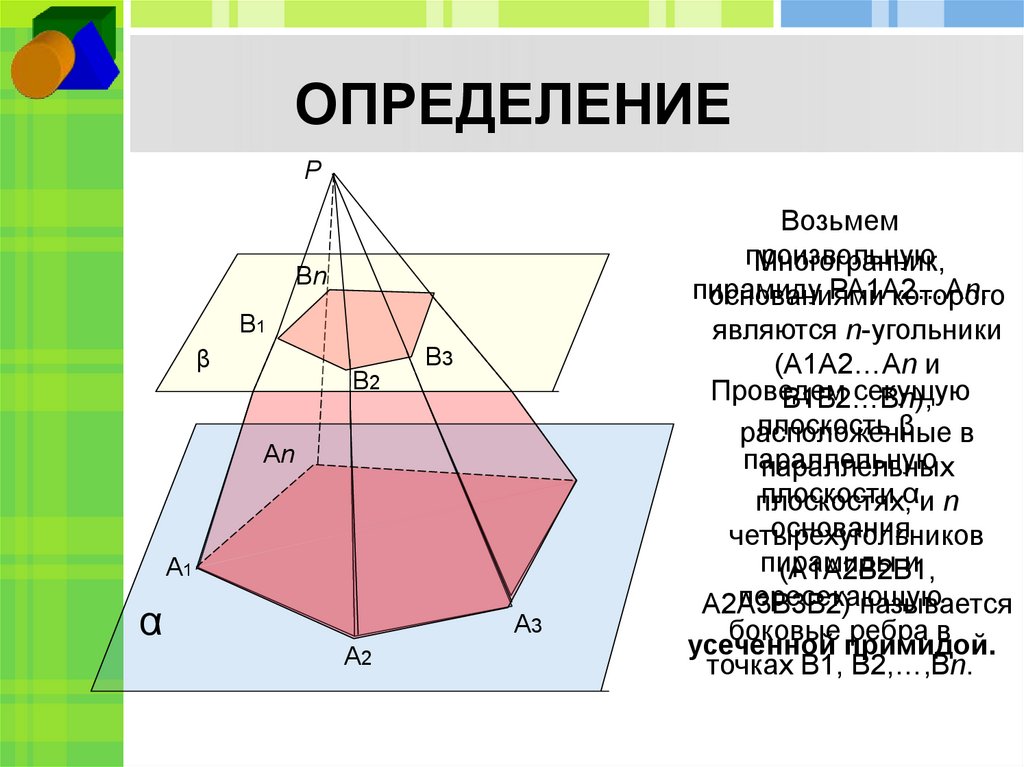
3. ОПРЕДЕЛЕНИЕ

Р
Вn
В1
β
В2
В3
Аn
А1
α
А3
А2
Возьмем
произвольную
Многогранник,
пирамиду
РА1А2…Аn.
основаниями
которого
являются n-угольники
(А1А2…Аn и
Проведем
секущую
В1В2…Вn),
плоскость β, в
расположенные
параллельную
параллельных
плоскости αи n
плоскостях,
основания
четырехугольников
пирамиды
и
(А1А2В2В1,
пересекающую
А2А3В3В2)
называется
боковые ребра в
усеченной примидой.
точках В1, В2,…,Вn.

4. Элементы усеченной пирамиды

Основания усеченной пирамиды
А1А2А3А4А5,
В5
В4
В1
В2
В1В2В3В4В5
Боковые грани усеченной пирамиды
В3
А1В1В2А2, А2В2В3А3, А3В3В4А4 и тд.
Ребра усеченной пирамиды
А5
А1А2, А2А3, А3А4, А4А5, А5А1,
А1В1, А2В2, А3В3, А4В4,А5В5 и тд.
А4
А1
А2
А3

5. Элементы усеченной пирамиды

В5
В1
В4
С
В2
Перпендикуляр, проведенный
из какой-нибудь точки одного
основания к плоскости
другого основания,
называется высотой
усеченной пирамиды.
В3
А5
А4
Н
А1
А2
А3
Отрезок СН является
высотой усеченной
пирамиды.

6. Боковые грани усеченной пирамиды – трапеции.

ДОКАЗАТЕЛЬСТВО:
В5
В4
β
В1
1)Рассмотрим боковую грань
А1А2В2В1:
А1А2 II В1В2
(А1А2 Є α, В1В2 Є β; α II β).
В3
В2
А1А2 и В1В2 не параллельны
(их продолжения пересекутся
в вершине Р)
А5
А4
α
А1
А2
А3
Данная грань – трапеция.
чтд.

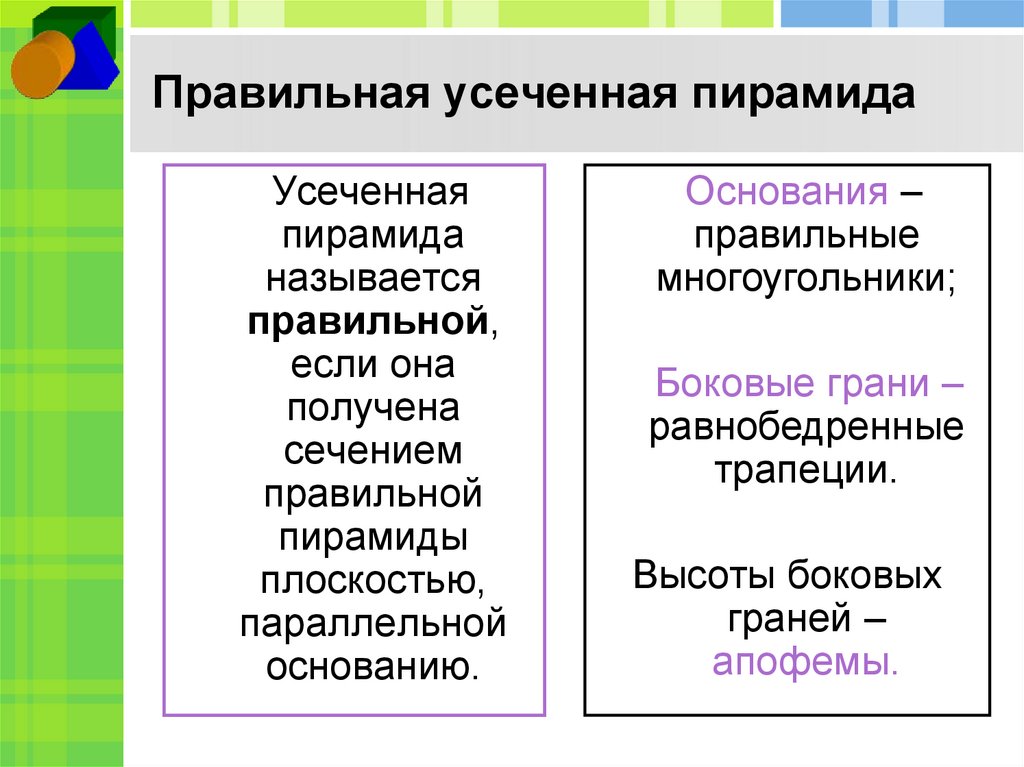
7. Правильная усеченная пирамида

Усеченная
пирамида
называется
правильной,
если она
получена
сечением
правильной
пирамиды
плоскостью,
параллельной
основанию.
Основания –
правильные
многоугольники;
Боковые грани –
равнобедренные
трапеции.
Высоты боковых
граней –
апофемы.

8.

Теорема:
площадь боковой поверхности правильной усеченной
пирамиды равна произведению полусуммы периметров
оснований на апофему.
Доказательство:
a1
a1
a1
a1
h
a1
a
a
a
1) Sбок=5 • Sтрапеции
(в правильной усеченной
пирамиде все грани
равны).
2) Pосн=5а
P1осн=5а1
Sтрапеции=(a +a1)/2•h
Sбок=(5а + 5а1)/2•h=
a
a
(Росн + Р1осн)/2•h.
чтд.