Геометрия. Площади многоугольников

1. Геометрия

2. Площади многоугольников

3.

1.
2.
3.
4.
5.
6.
7.
Площадь многоугольника.
Основные свойства площадей.
Площадь прямоугольника.
Площадь параллелограмма.
Площадь треугольника.
Площадь трапеции.
Площадь ромба.

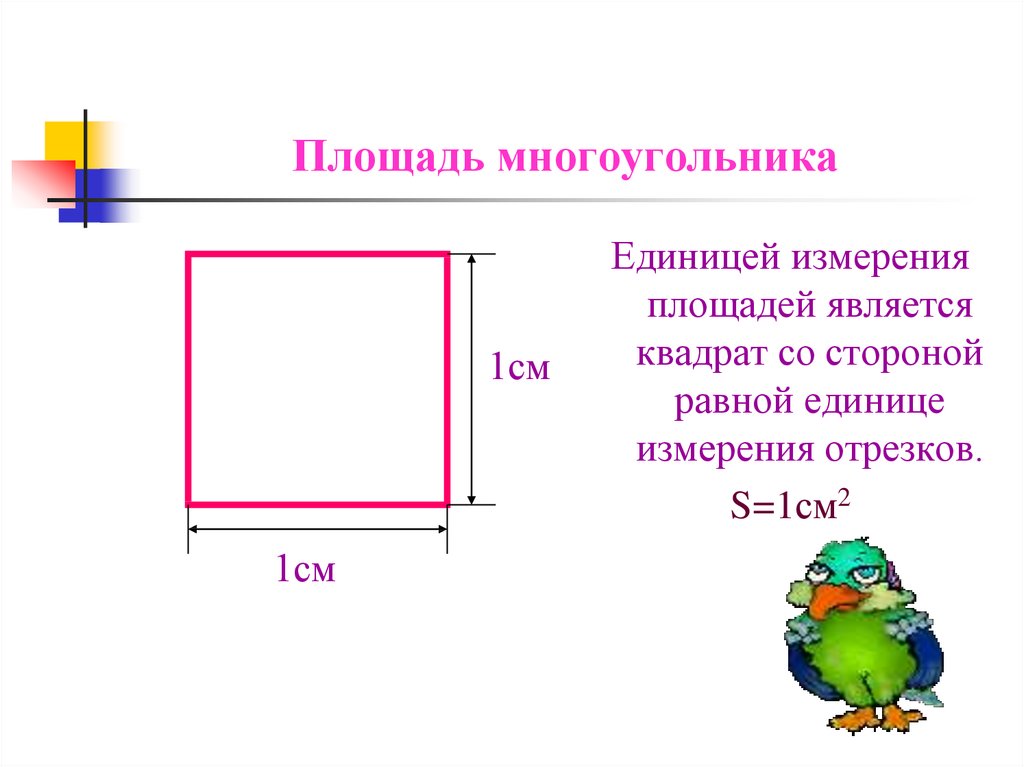
4. Площадь многоугольника

1см
1см
Единицей измерения
площадей является
квадрат со стороной
равной единице
измерения отрезков.
S=1см2

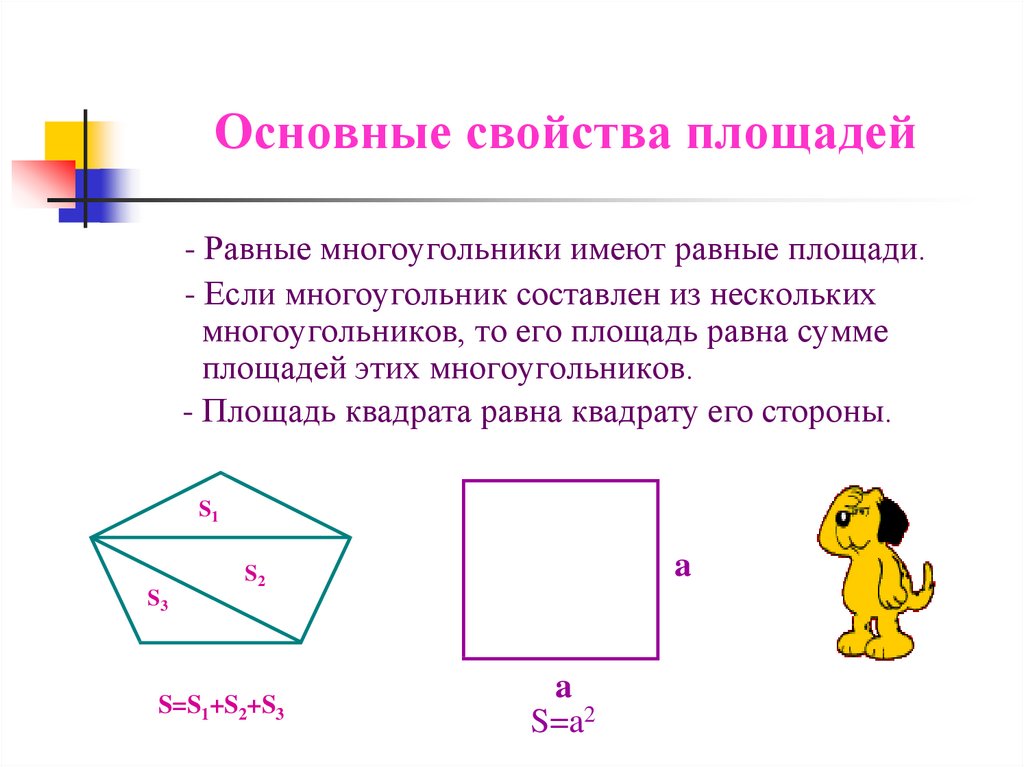
5. Основные свойства площадей

- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких
многоугольников, то его площадь равна сумме
площадей этих многоугольников.
- Площадь квадрата равна квадрату его стороны.
S1
a
S2
S3
S=S1+S2+S3
a
S=a2

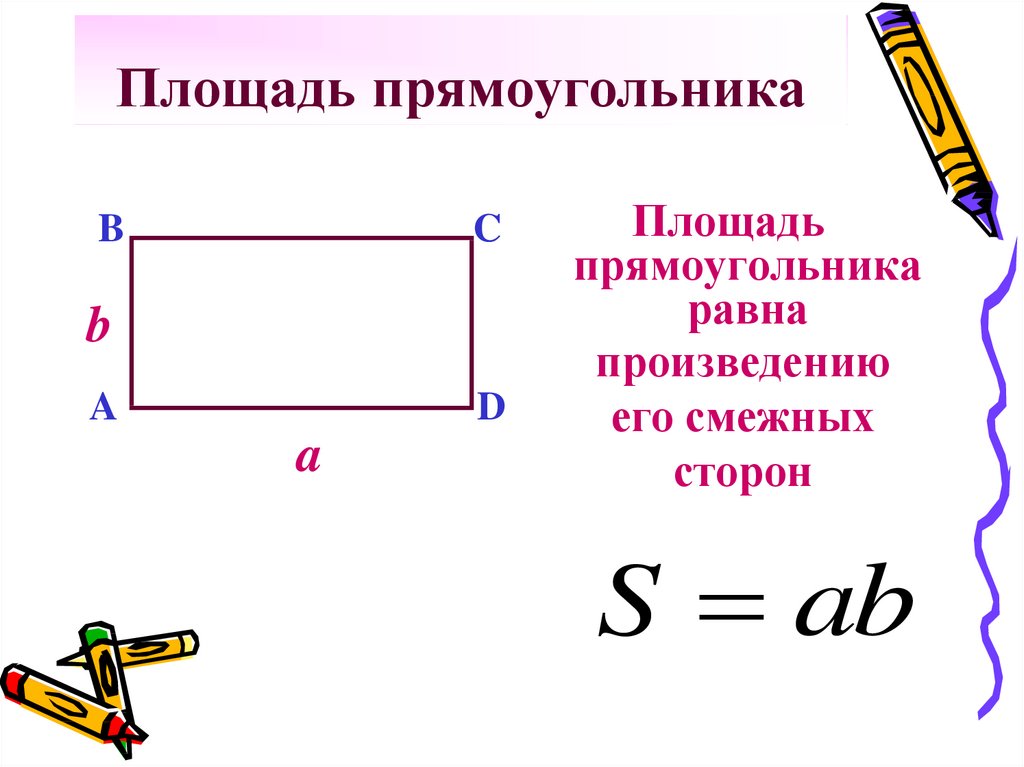
6. Площадь прямоугольника

B
C
b
A
D
a
Площадь
прямоугольника
равна
произведению
его смежных
сторон
S ab

7. Площадь параллелограмма

a
B
C
h
A
D
Площадь
параллелограмм
равна
произведению его
основания
на высоту.
S ah

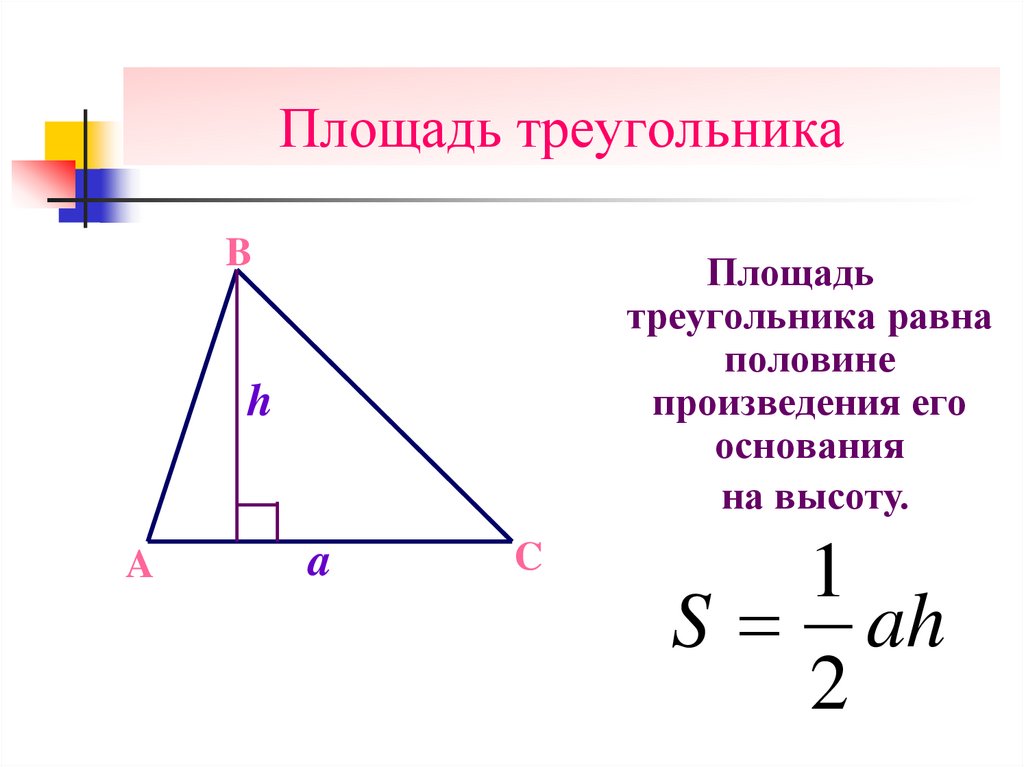
8. Площадь треугольника

B
Площадь
треугольника равна
половине
произведения его
основания
на высоту.
h
A
a
C
1
S ah
2

9. Площадь треугольника

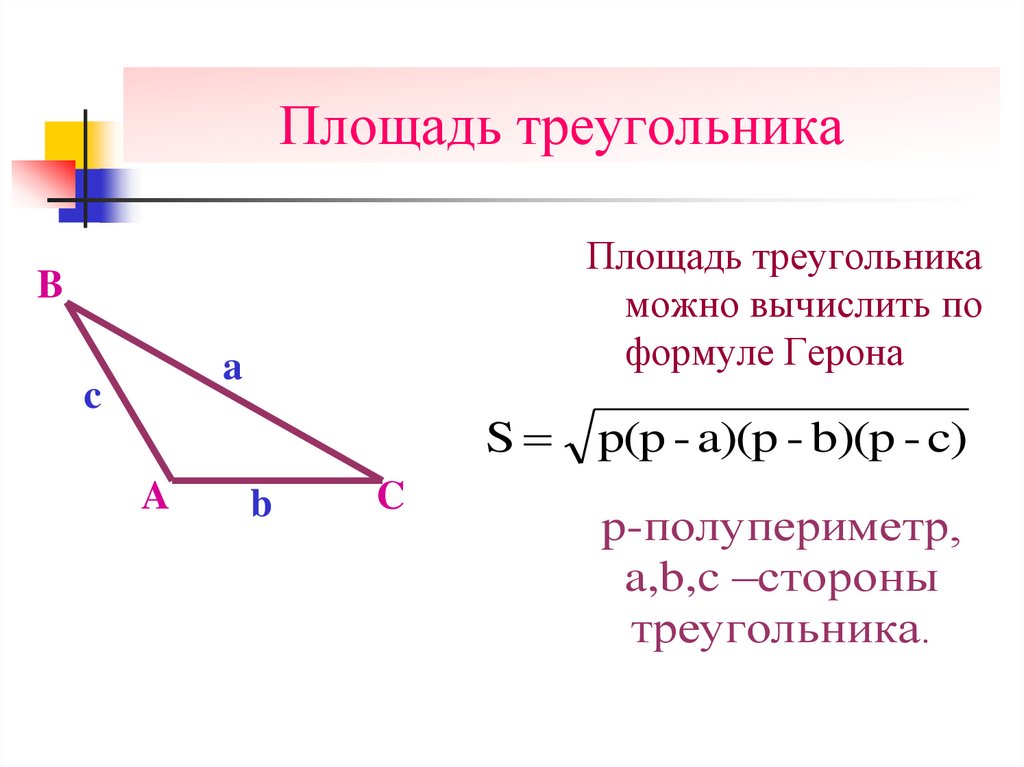
Площадь треугольника
можно вычислить по
формуле Герона
B
a
c
S
A
b
C
p(p - a)(p - b)(p - c)
p-полупериметр,
a,b,c –стороны
треугольника.

10. Площадь треугольника

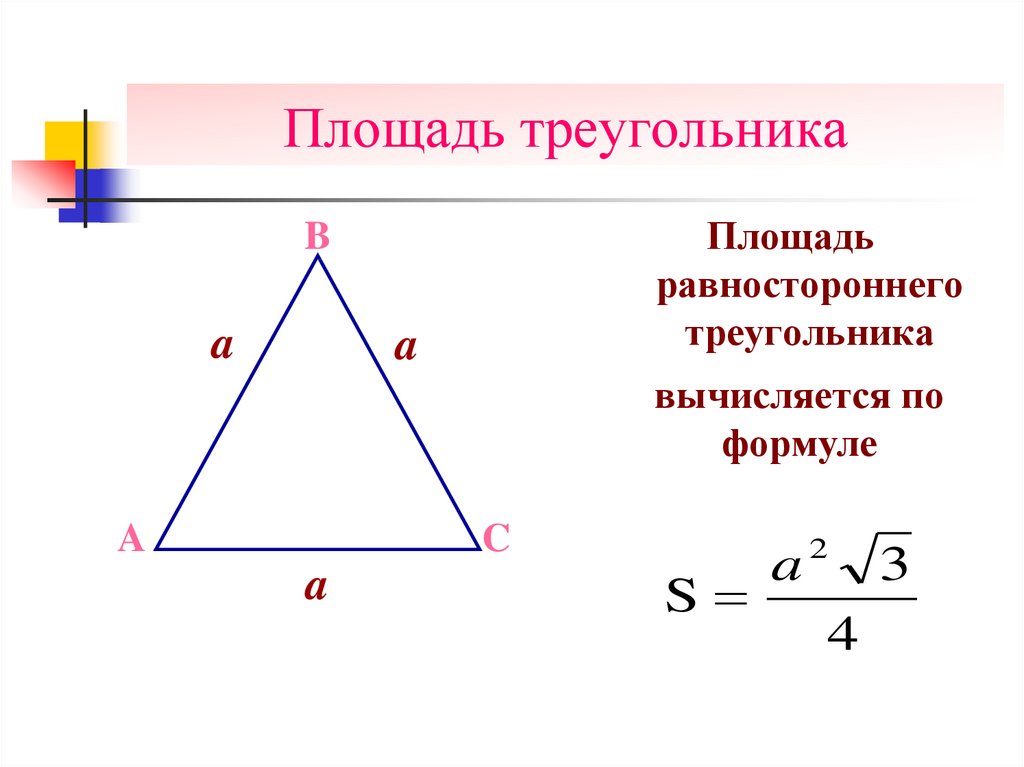
Площадь
равностороннего
треугольника
B
a
a
вычисляется по
формуле
A
C
a
a2 3
S
4

11. Площадь треугольника

Следствие 1. Площадь прямоугольного треугольника
равна произведения его катетов.
Следствие 2. Если высоты двух треугольников равны,
то их площади относятся как основания.

12. Площадь треугольника

Если угол одного треугольника
равен
углу другого треугольника, то
B
s
B1
C
A
площади этих треугольников
относятся
сторон,
как
произведения
заключающих
равные
углы.
s1
A1
C1
S
AB AC
S1 A1B1 A2 B2

13. Площадь трапеции.

b
B
C
h
A
a
D
Площадь трапеции
равна произведению
полусуммы ее
оснований
на высоту.
S
a b
2
h

14. Площадь трапеции.

B
E
A
Площадь трапеции
равна
C
h
произведению средней
линии
на высоту.
F
D
S EF h

15. Площадь ромба.

B
d1
d2
A
D
C
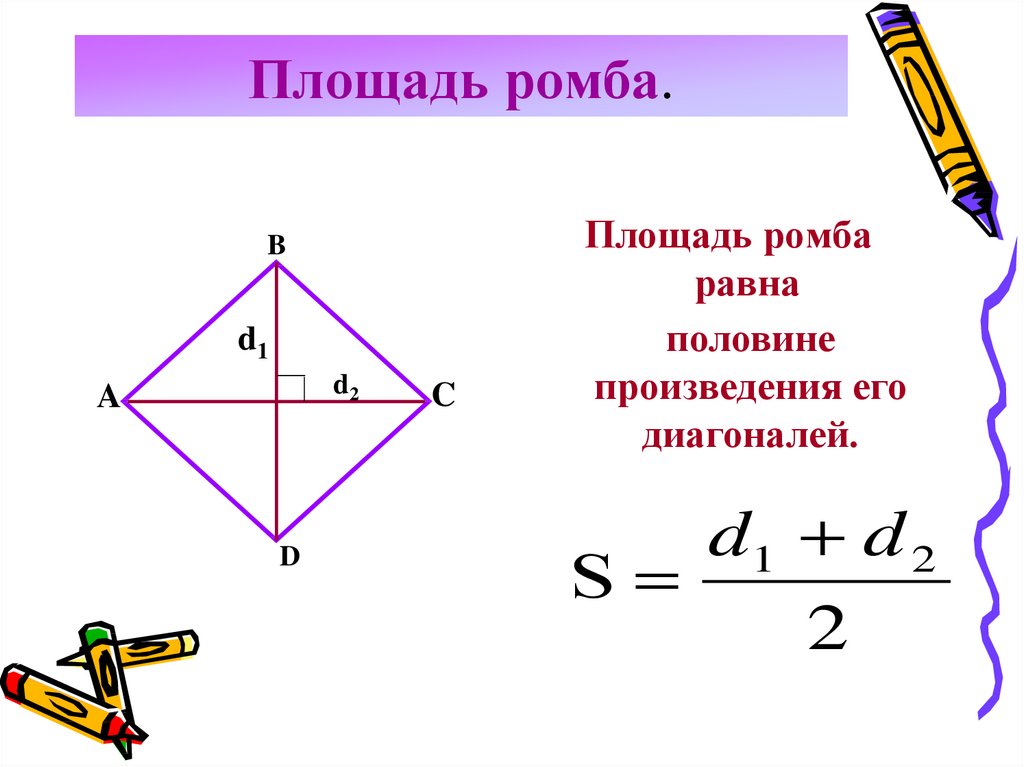
Площадь ромба
равна
половине
произведения его
диагоналей.
d1 d 2
S
2