Similar presentations:
Площадь геометрических фигур
1.
2.
Понятие площадиПлощадь квадрата
Площадь прямоугольника
Площадь треугольника
Площадь прямоугольного треугольника
Площадь параллелограмма
Площадь трапеции
3.
Понятие площадиПонятие площади многоугольника
Измерение площади
Свойства площадей
Содержание
4. Площадь многоугольника – это величина той части плоскости которую занимает многоугольник
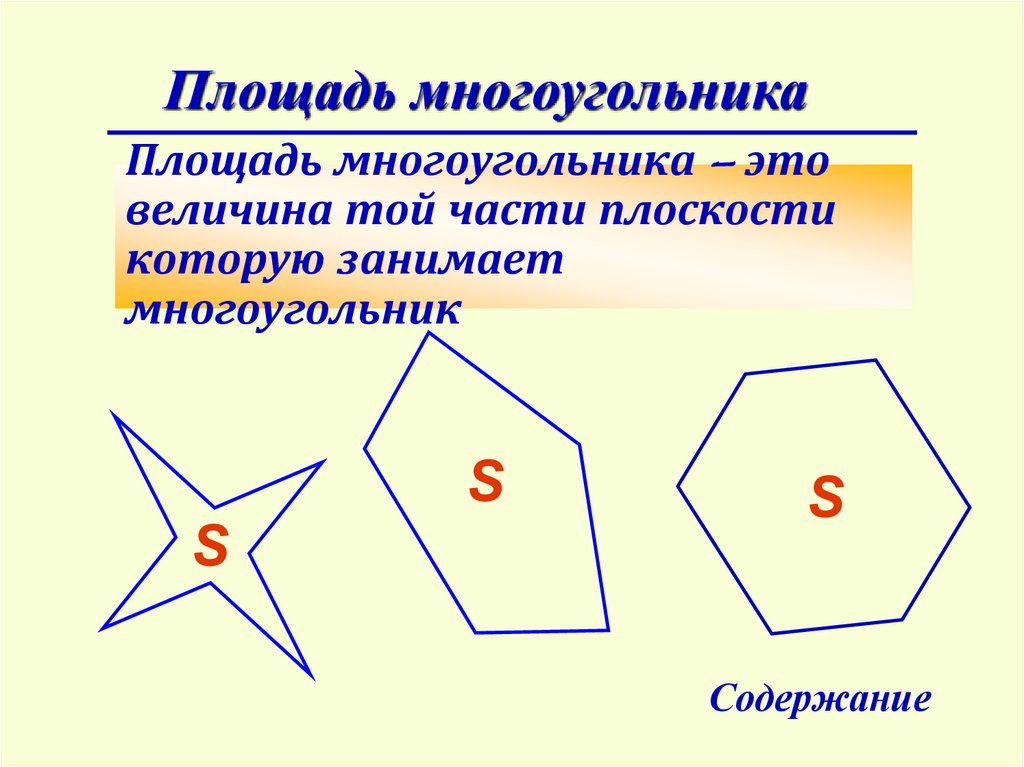
Площадь многоугольникаПлощадь многоугольника – это
величина той части плоскости
которую занимает
многоугольник
Содержание
5.
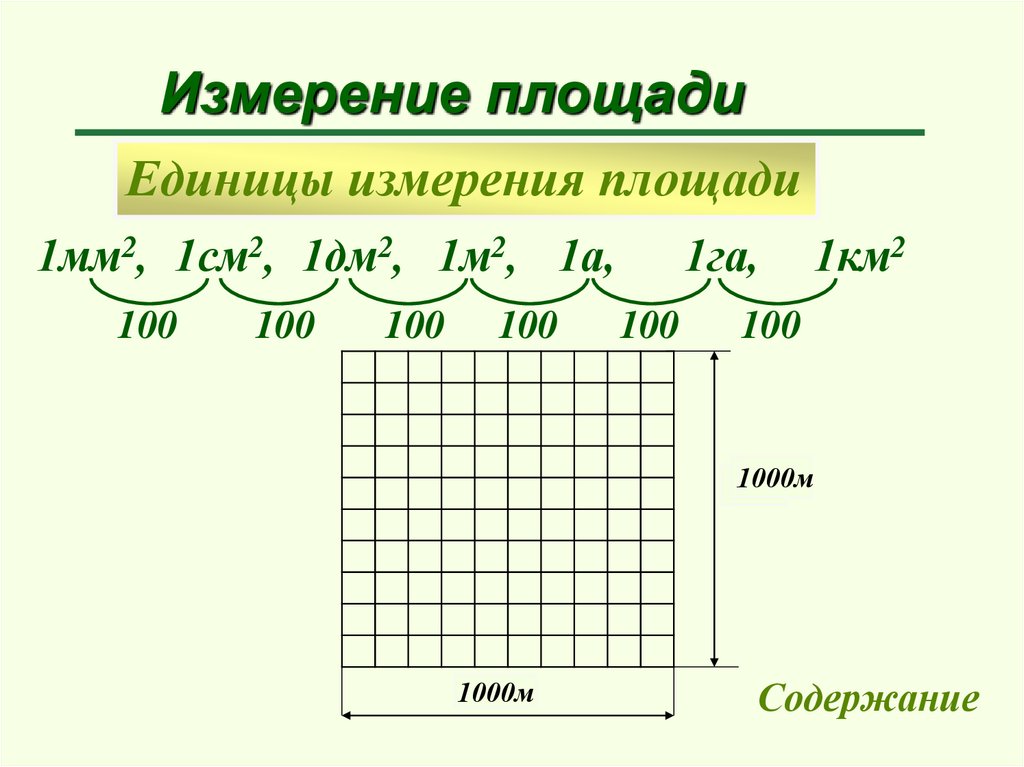
Измерение площадиЕдиницы измерения площади
1мм2, 1см2, 1дм2, 1м2, 1а,
100
100
100
100
1га,
100
1км2
100
1000м
110м
1100м
дм
м
1см
1см
1000м
100м
110
1дм
мм
Содержание
6.
Измерение площади1 см
1 см
10
11
12
7
8
9
4
5
6
1
2
3
1 см
1 см
S 2,14 cм2
S=12 cм2
Содержание
7.
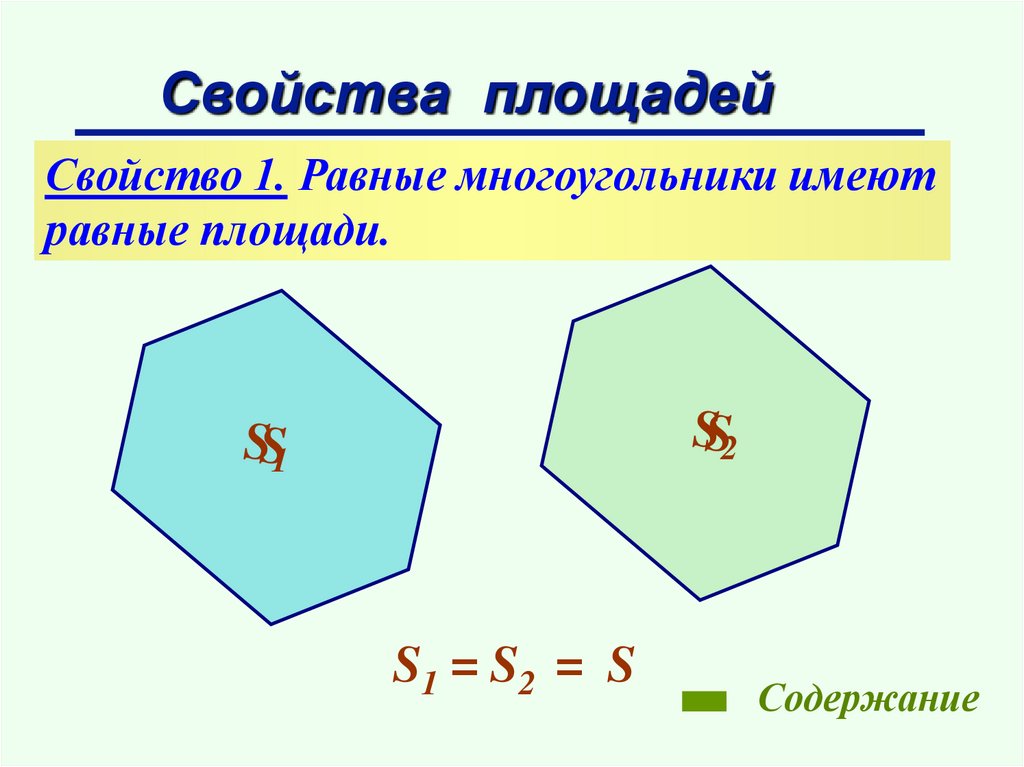
Свойства площадейСвойство 1. Равные многоугольники имеют
равные площади.
SS2
SS1
S1 = S2 = S
Содержание
8.
Свойства площадейСвойство 2. Если многоугольник составлен
из нескольких многоугольников, то его
площадь равна сумме площадей этих
многоугольников.
S1
S2
S3
S1 + S 2 + S3 = S
Содержание
9.
Свойства площадейСвойство 3. Площадь квадрата равна
квадрату его стороны.
21 22 23 24 25
16 17 18 19 20
5 11 12 13 14 15
6 7 8 9 10
1 2 3 4 5
5
S= 5∙5 =25
Содержание
10.
Свойства площадейСвойство 3. Площадь квадрата равна
квадрату его стороны.
S= а∙а = а2
а
а
Содержание
11.
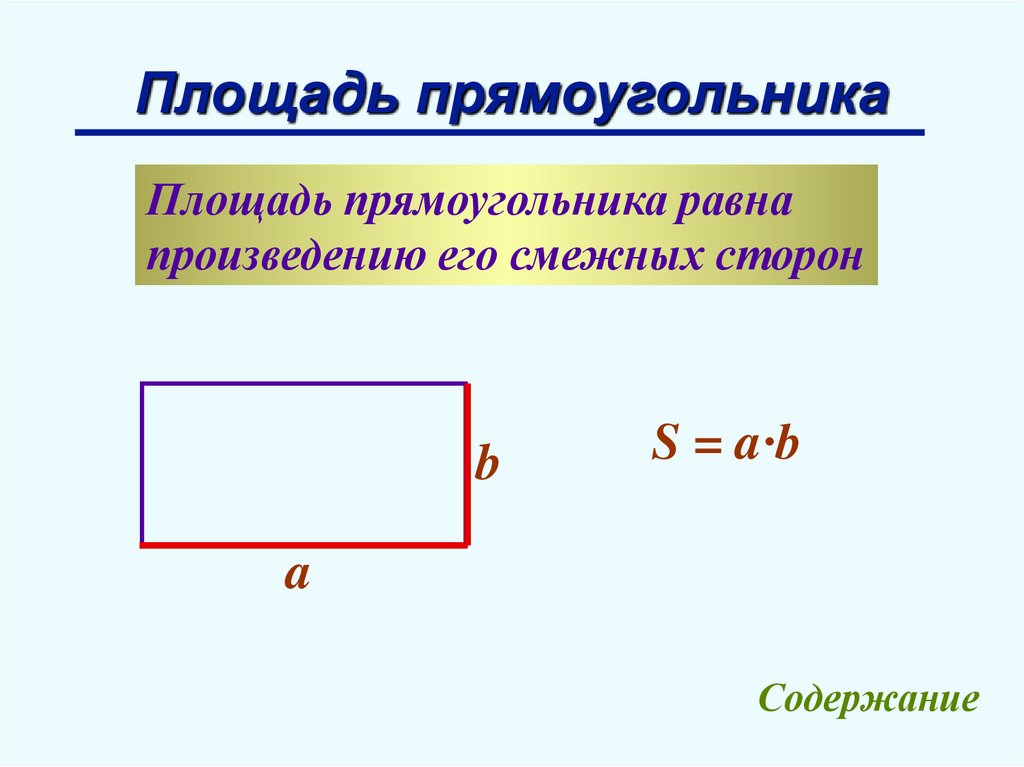
Площадь прямоугольникаПлощадь прямоугольника равна
произведению его смежных сторон
b
S = a∙b
a
Содержание
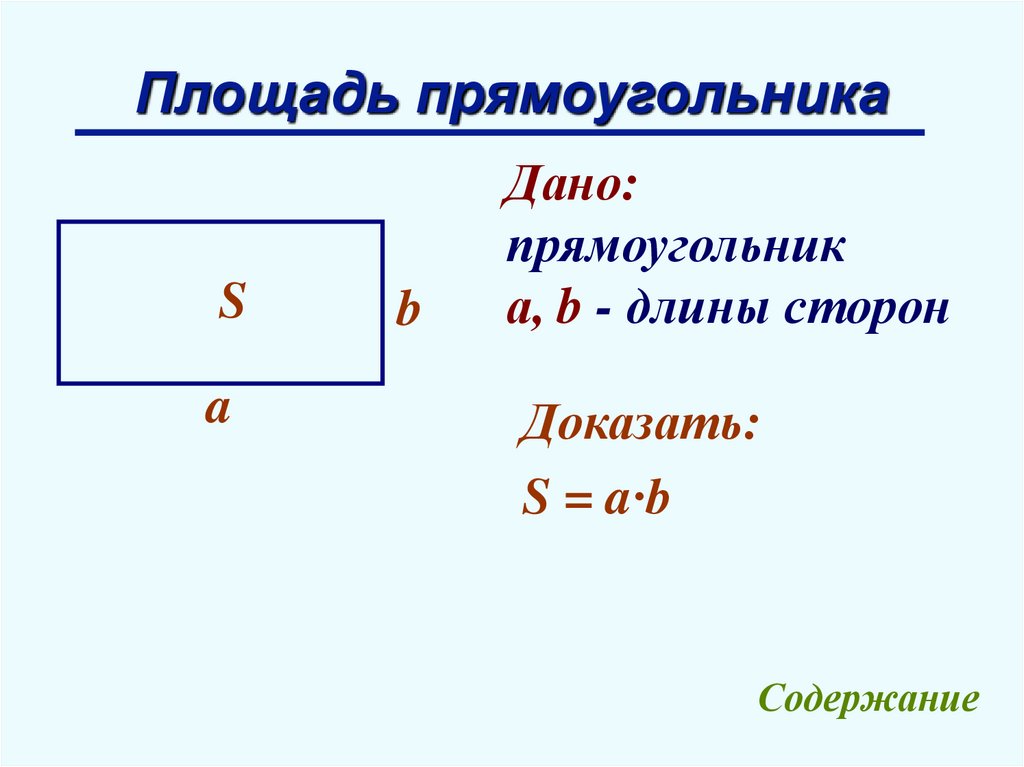
12.
Площадь прямоугольникаS
a
b
Дано:
прямоугольник
а, b - длины сторон
Доказать:
S = a∙b
Содержание
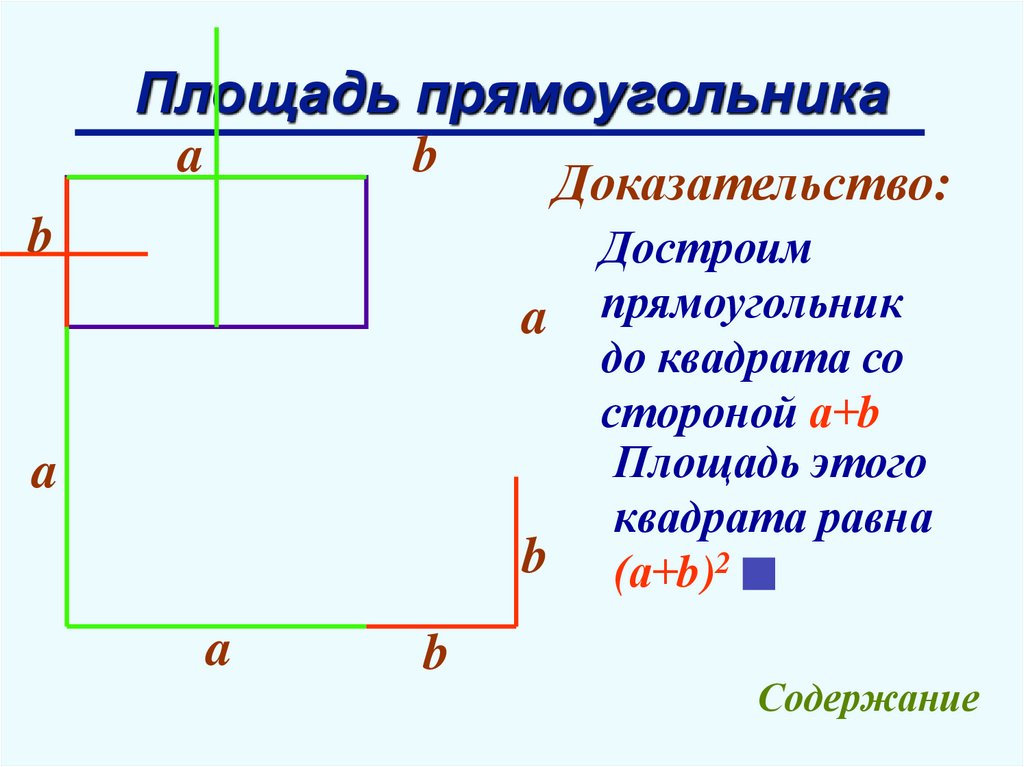
13.
Площадь прямоугольникаa
b
Доказательство:
b
a
a
b
a
b
Достроим
прямоугольник
до квадрата со
стороной а+b
Площадь этого
квадрата равна
(а+b)2
Содержание
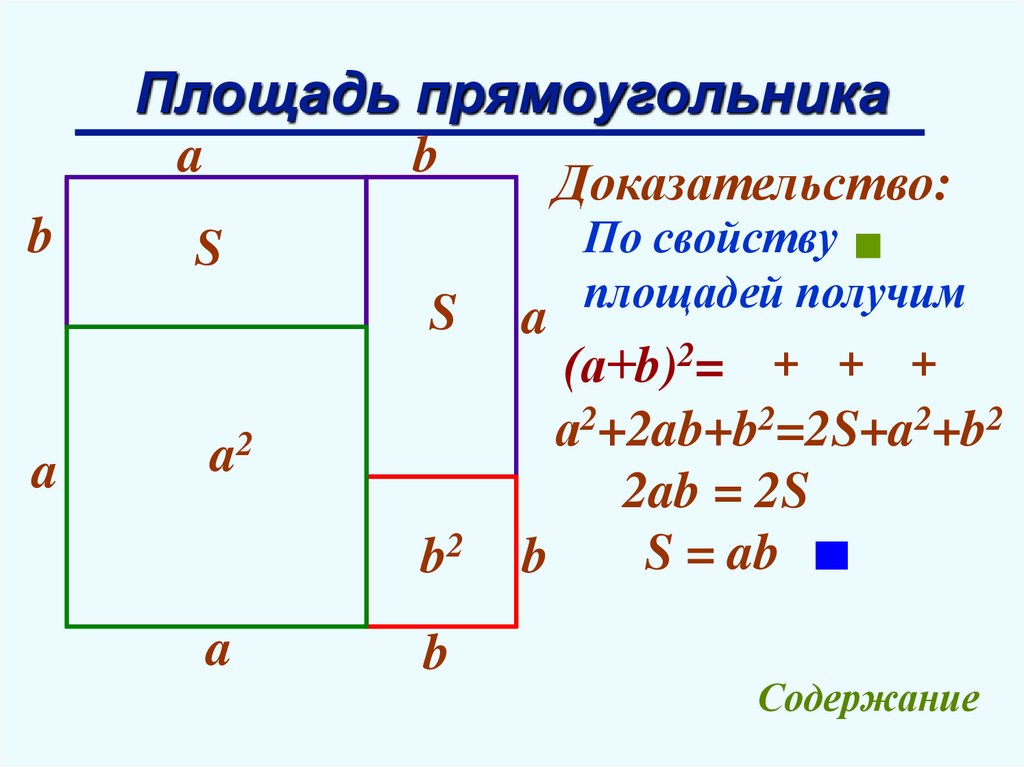
14.
Площадь прямоугольникаa
b
b
S
S
a
a2
b2
a
b
Доказательство:
Полученный квадрат
состоит из двух
a
прямоугольников с
площадью S и
двух квадратов с
площадями а2 и b2.
b
Содержание
15.
Площадь прямоугольникаa
b
b
S
S
a
Доказательство:
a2
b2
a
b
a
По свойству
площадей получим
(а+b)2= + + +
а2+2ab+b2=2S+a2+b2
2ab = 2S
S = ab
b
Содержание
16.
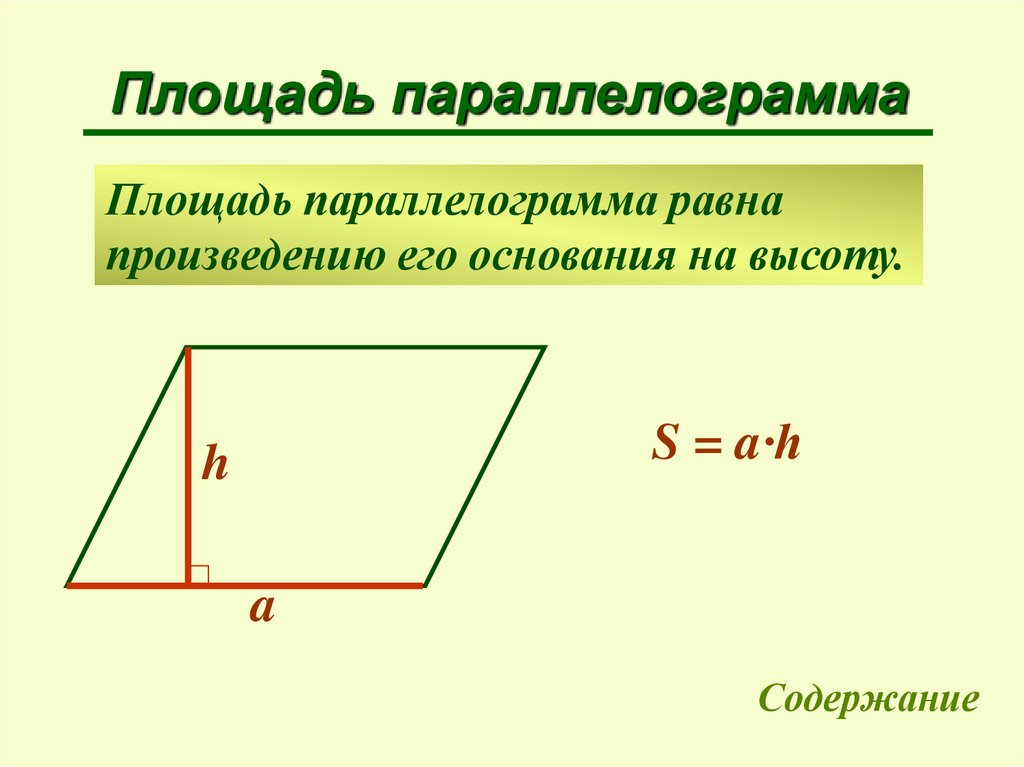
Площадь параллелограммаПлощадь параллелограмма равна
произведению его основания на высоту.
S = a∙h
h
a
Содержание
17.
Площадь параллелограммаB
C
Дано:
АВСD-параллелограмм
Доказать:
A
H
D
S = AD∙BH
Содержание
18.
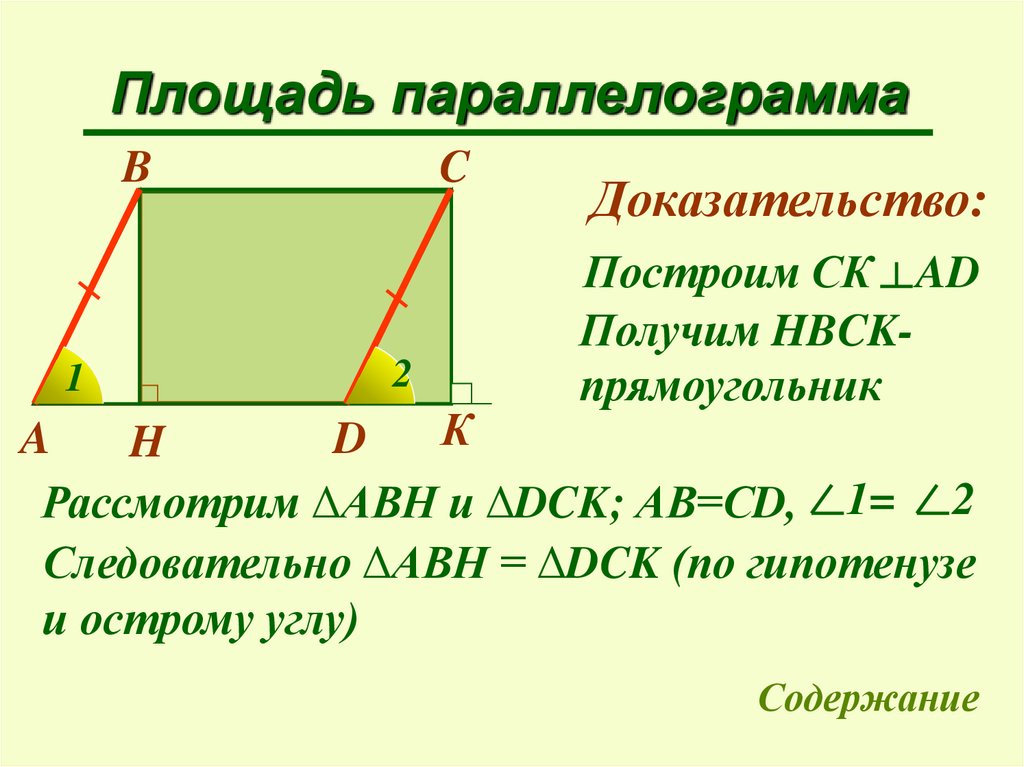
Площадь параллелограммаB
1
C
2
Доказательство:
Построим СК AD
Получим HBCKпрямоугольник
К
A
D
H
Рассмотрим ΔАВН и ΔDCK; АВ=СD, 1= 2
Следовательно ΔАВН = ΔDCK (по гипотенузе
и острому углу)
Содержание
19.
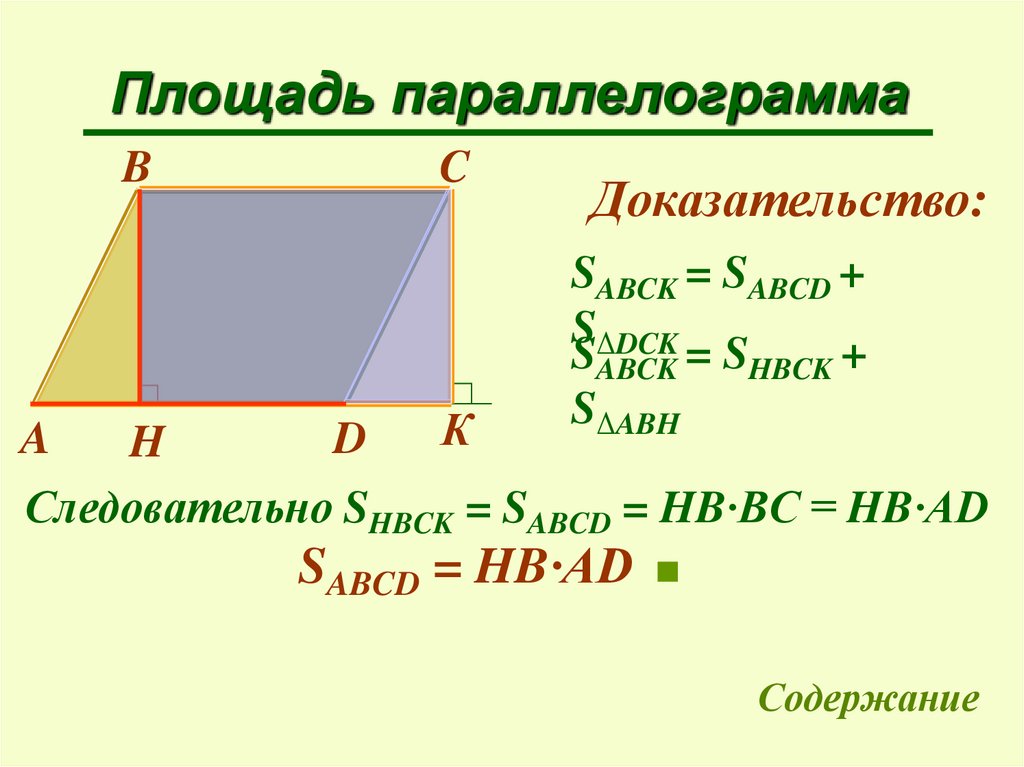
Площадь параллелограммаB
C
Доказательство:
SABCK = SABCD +
SΔDCK
SABCK = SHBCK +
SΔABH
К
D
H
Следовательно SHBCK = SABCD = HB∙BC = HB∙AD
A
SABCD = HB∙AD
Содержание
20.
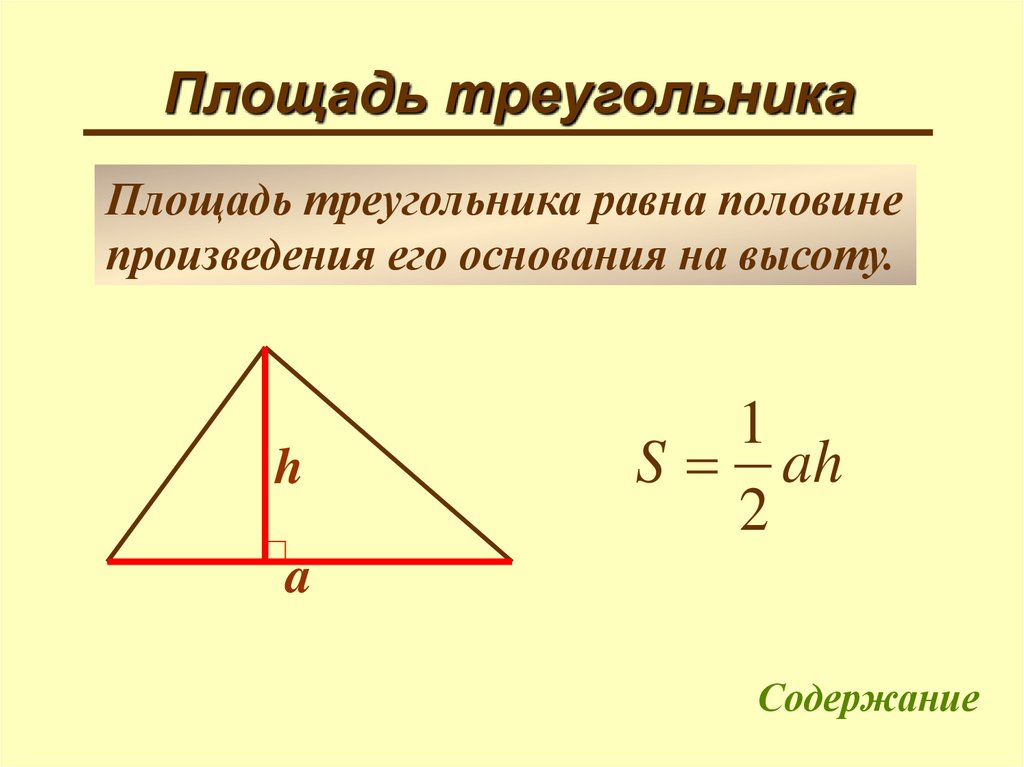
Площадь треугольникаПлощадь треугольника равна половине
произведения его основания на высоту.
h
1
S ah
2
a
Содержание
21.
Площадь треугольникаB
Дано:
ΔАВС; BН
АC
Доказать:
A
H
C
1
S = AC∙BH
2
Содержание
22.
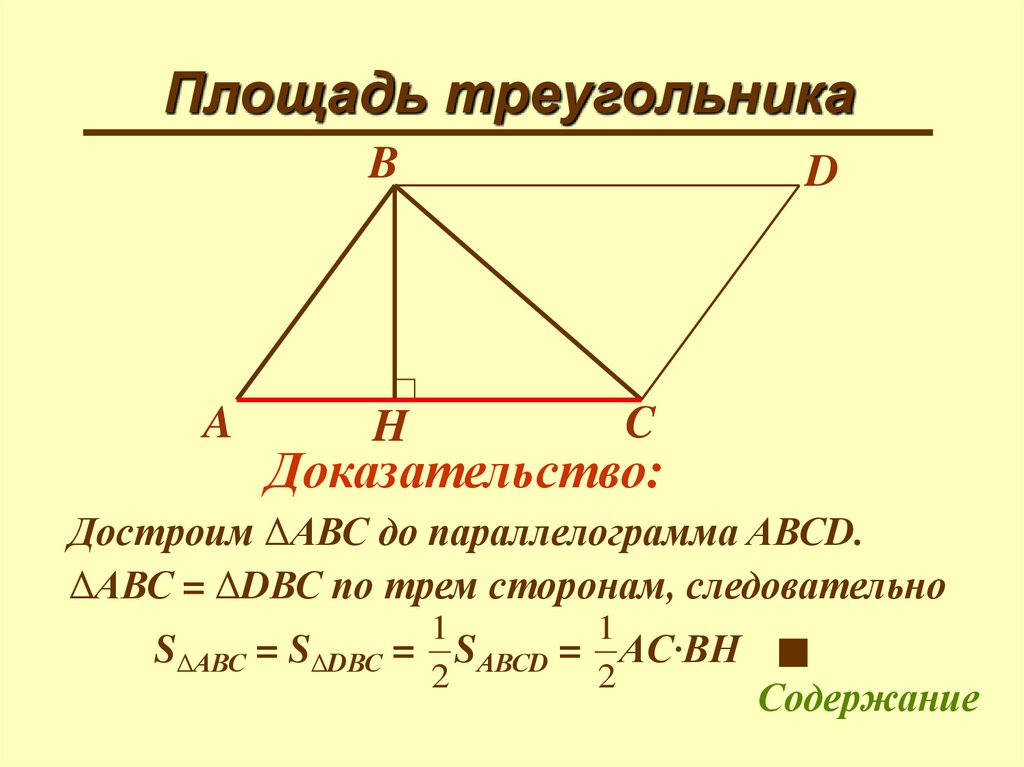
Площадь треугольникаB
A
H
D
C
Доказательство:
Достроим ΔАВС до параллелограмма АВСD.
ΔАВС = ΔDВС по трем сторонам, следовательно
1
1
SΔАВС = SΔDВС = SАВСD = AC∙BH
2
2
Содержание
23.
Площадь прямоугольноготреугольника
Площадь прямоугольного треугольника
равна половине произведения катетов
1
S= a∙b
2
а
b
Содержание
24.
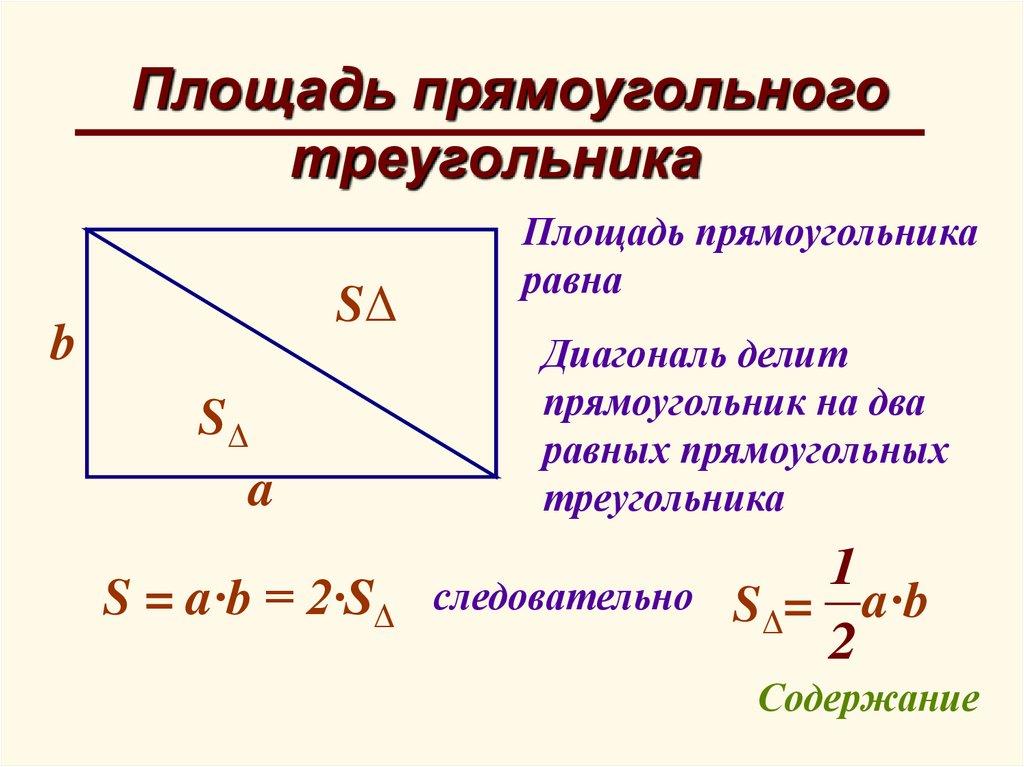
Площадь прямоугольноготреугольника
b
SΔ
S=a∙b
SΔ
a
S = a∙b = 2∙SΔ
Площадь прямоугольника
равна
Диагональ делит
прямоугольник на два
равных прямоугольных
треугольника
следовательно
1
SΔ= a∙b
2
Содержание
25.
Площадь трапецииПлощадь трапеции равна произведению
полусуммы ее оснований на высоту.
b
1
S a b h
2
h
a
Содержание
26.
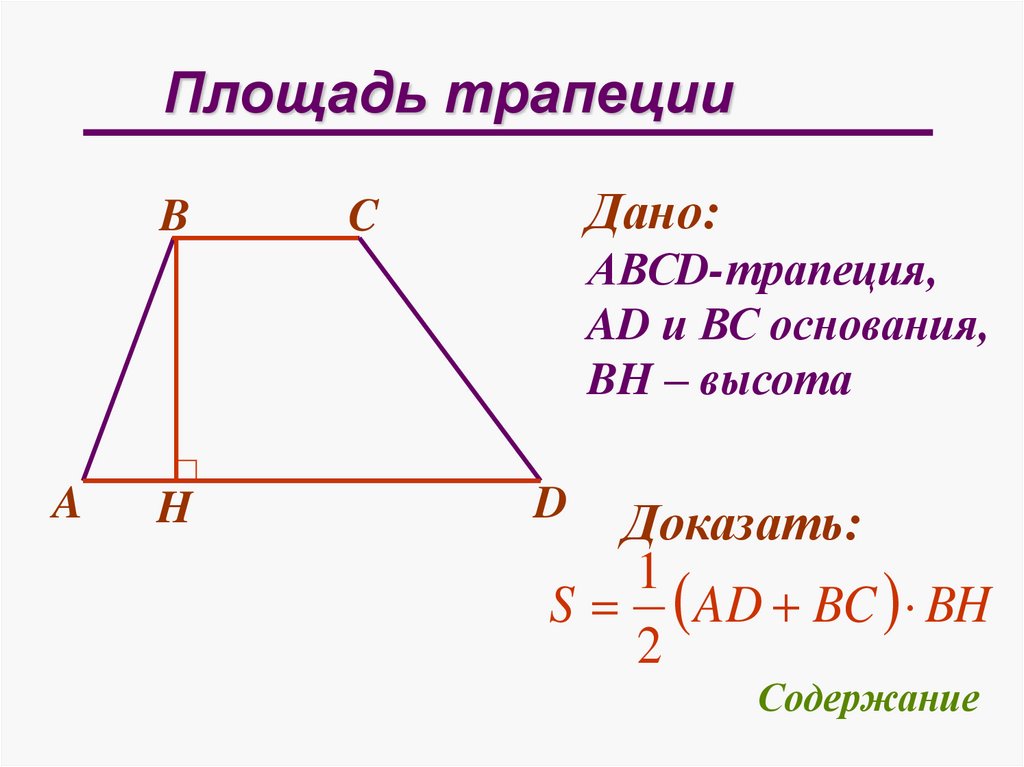
Площадь трапецииB
Дано:
C
АВСD-трапеция,
AD и ВС основания,
BH – высота
A
H
D
Доказать:
1
S AD BC BH
2
Содержание
27.
Площадь трапецииВ
С
P
Доказательство:
Построим диагональ BD,
получим ΔABD и ΔBDC
1
S ABD AD BH
2
1
H
А
D
S СBD ВС DP
2
HBPD – прямоугольник, следовательно ВН=PD
1
1
1
S AD BH BC BH AD BC BH
2
2
2
Содержание














 mathematics
mathematics








