Теория активированного комплекса

1.

Теория активированного комплекса.
3. Основные положения и вывод выражения для
константы скорости.

2.

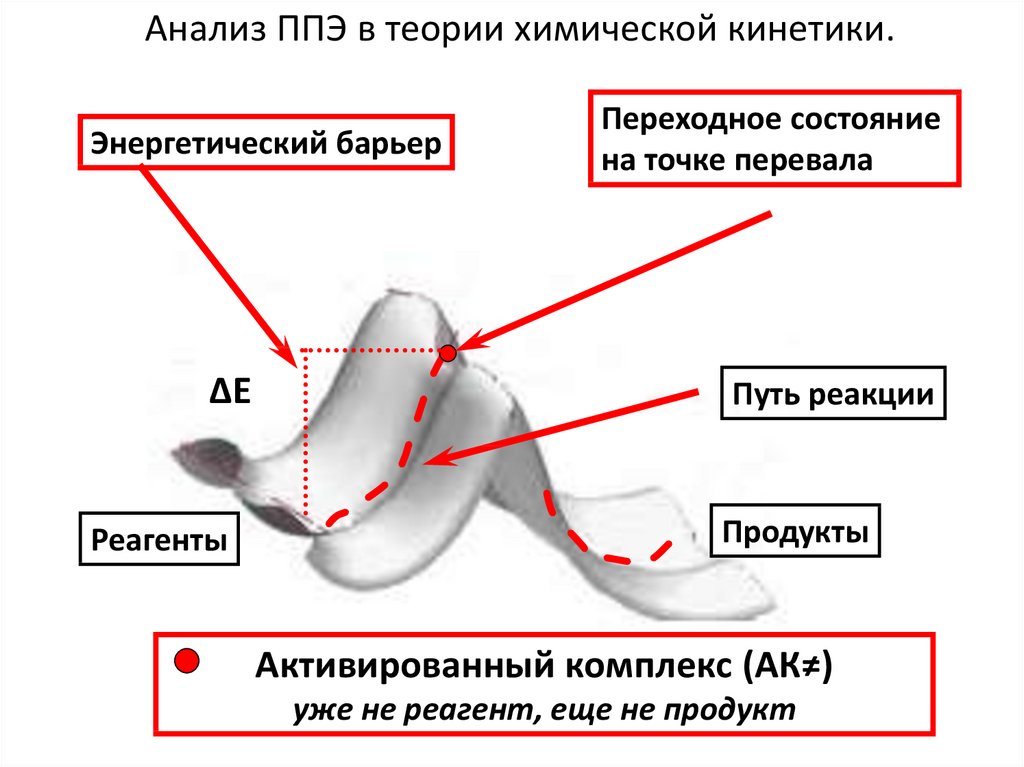
Анализ ППЭ в теории химической кинетики.
Энергетический барьер
∆Е
Реагенты
Переходное состояние
на точке перевала
Путь реакции
Продукты
Активированный комплекс (АК≠)
уже не реагент, еще не продукт

3.

Свойства активированного комплекса
(АК≠)
АК≠ - конфигурация в области
седловой точки на ППЭ
(минимальный максимум энергии,
перевал).
А..В..С
(АВС≠)
АВ
ВС
Конфигурация атомов в АК≠ является переходной между
конфигурациямми реагентов и продуктов.
АК≠ существует в некоторой малой области δ, а не в
единственной точке.
АК≠ имеет на одну поступательную степень свободы
больше, чем устойчивая частица.
АК≠ имеет на одну колебательную степень свободы
меньше, чем устойчивая молекула, состоящая из такого
же числа атомов.
Не путать АК≠ и промежуточным веществом!!

4.

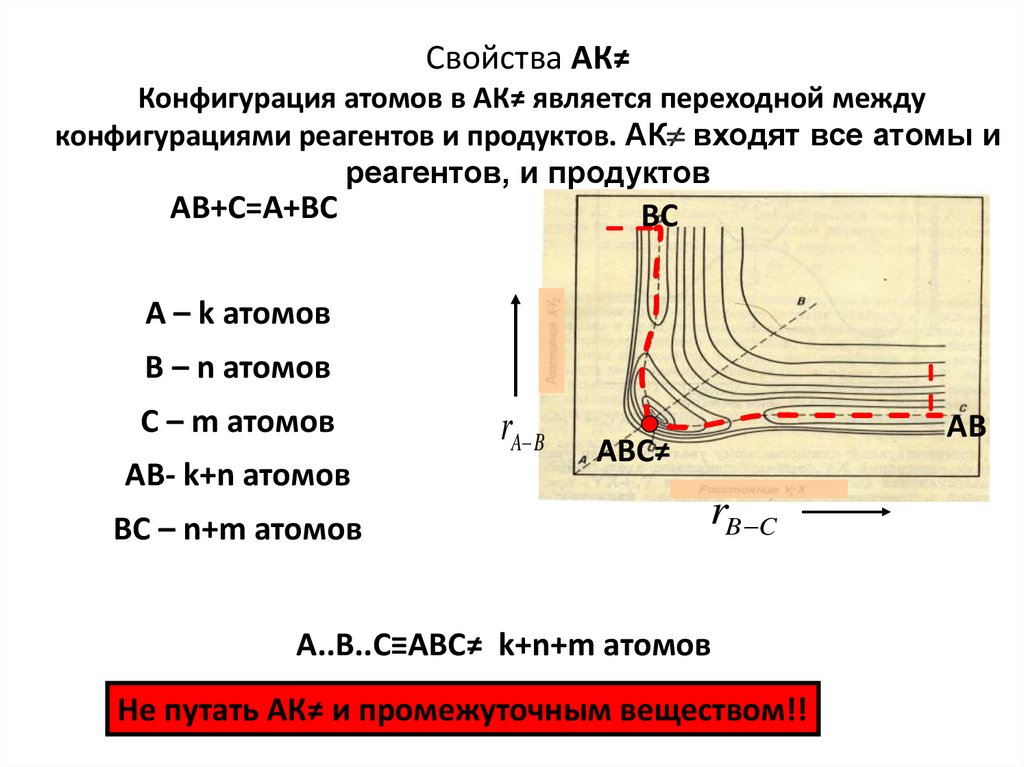
Свойства АК≠
Конфигурация атомов в АК≠ является переходной между
конфигурациями реагентов и продуктов. АК входят все атомы и
реагентов, и продуктов
АВ+С=А+ВС
ВС
А – k атомов
В – n атомов
С – m атомов
АВ- k+n атомов
ВС – n+m атомов
rA B
АВ
АВС≠
rB C
А..В..С≡АВС≠ k+n+m атомов
Не путать АК≠ и промежуточным веществом!!

5.

Время
АВ+С=А+ВС
Свойства
АК≠жизни АК≠
АК≠ существует в некоторой малой области δ, а не в
единственной точке. АК≠ имеет на одну поступательную
степень свободы больше, чем устойчивая частица.
δ
Е
Vк. р.
АВ
ВС
δ область
путь реакции
АВС≠
kT
V
к.р.
2
m
скорость движения АК≠ в области δ
в направлении координаты реакции (к.р.)
длина области в направлении координаты реакции (к.р.) - δ
(
2
m
kT
)
Q
h
t
к
.р
.
1
/2
1
2

6.

АК≠ имеет на одну колебательную степень свободы меньше, чем
устойчивая молекула, состоящая из такого же числа атомов.
Е
X1-путь реакции,
X2 –координата в сечении
в сечении минимум функции Е
колебание есть!
в сечении максимум функции E
колебания нет!
2
E
E
1 k2
0
,k
0
2
2
2
x
x
2
2
2
2
E
E
1 k1
0
,k
0
1
1
2
x
x
2
1
1
частота колебания гармонического осциллятора ν1 мнимая

7.

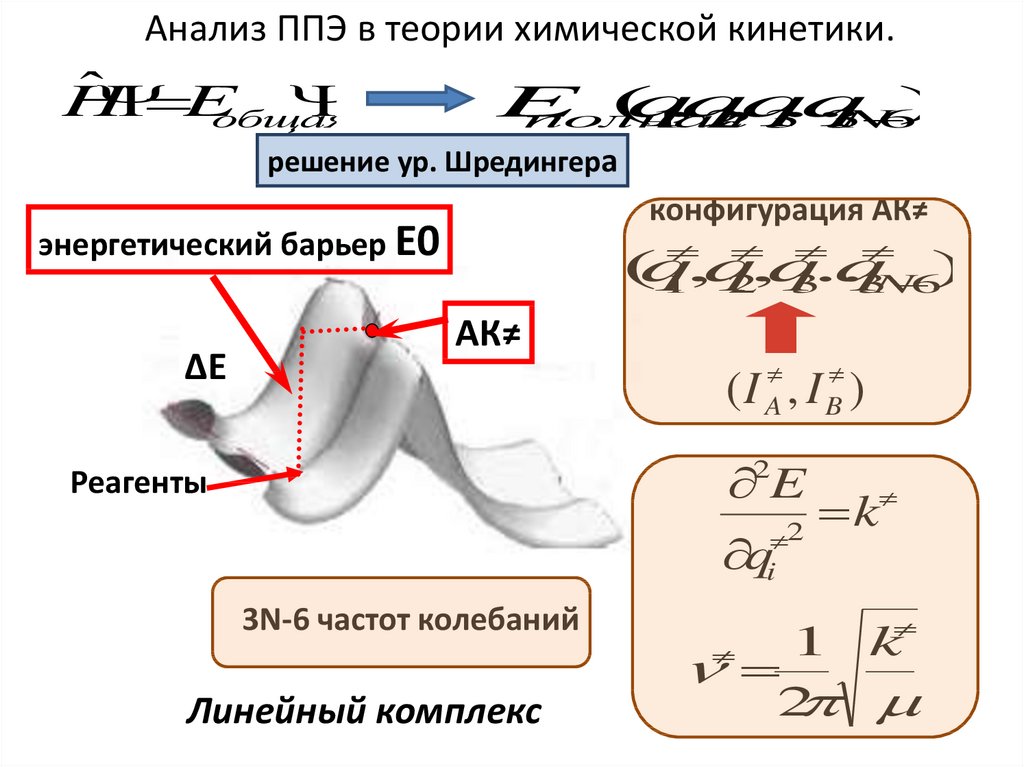
Анализ ППЭ в теории химической кинетики.
Ĥ
E
общая
E
(
q
,q
,q
..
q
)
полная
1
2
3
3
N
6
решение ур. Шредингера
конфигурация АК≠
энергетический барьер Е0
∆Е
1
2 3
3
N
6
(q,q,q..
q )
АК≠
( I A , I B )
E
2
Реагенты
2
i
q
3N-6 частот колебаний
k
1 k
2
Линейный комплекс

8.

Анализ ППЭ в теории химической кинетики.
Ĥ
E
общая
E
(
q
,q
,q
..
q
)
полная
1
2
3
3
N
6
решение ур. Шредингера, знаем координаты АК знаем
конфигурация АК≠
энергетический барьер Е0
∆Е
1
2 3
3
N
6
(q,q,q..
q )
АК≠
(IA , IB , IC )
E
2
Реагенты
2
i
q
3N-7 частот колебаний
k
1 k
2
Нелинейный комплекс

9.

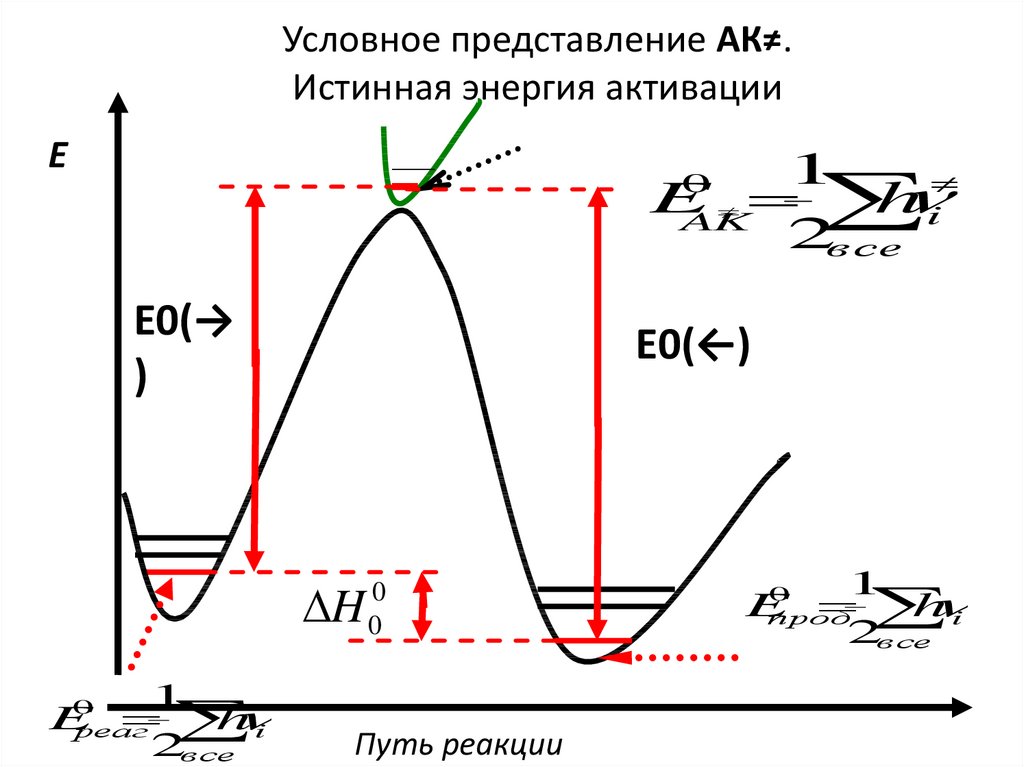
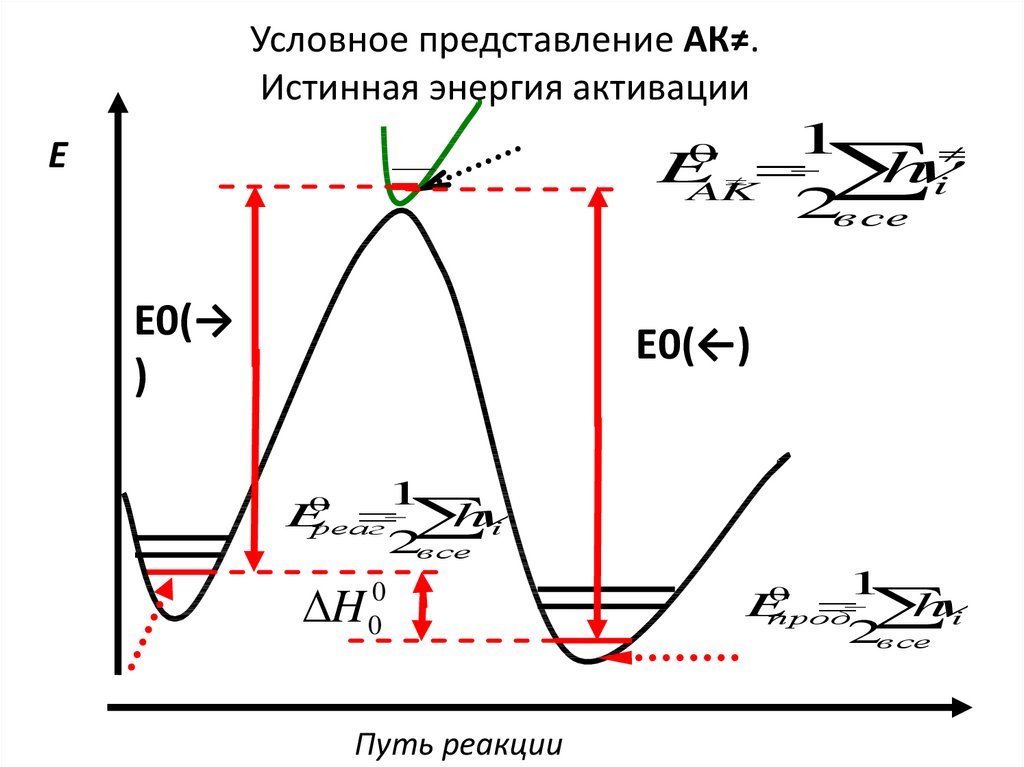
Условное представление АК≠.
Истинная энергия активации
E
1
E
h
i
2в се
0
AK
E0(→
)
E0(←)
H
1
0
E
h
i
реаг
2все
0
0
Путь реакции
1
E
h
i
2все
0
прод

10.

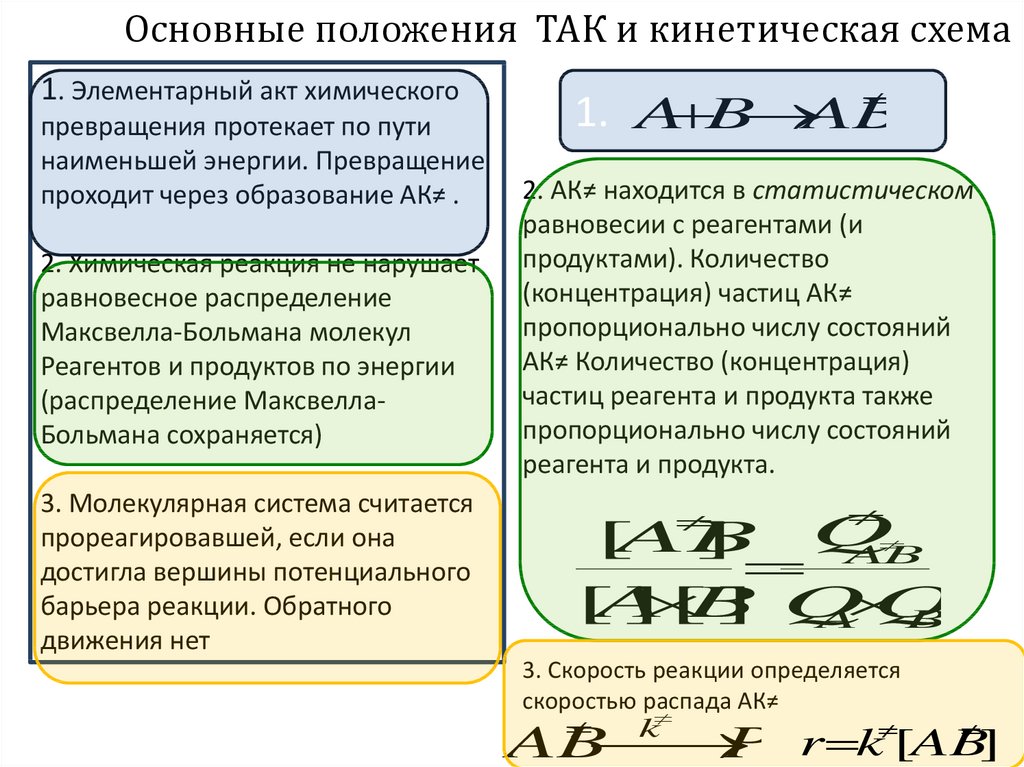
Основные положения ТАК и кинетическая схема
1. Элементарный акт химического
превращения протекает по пути
наименьшей энергии. Превращение
проходит через образование АК≠ .
2. Химическая реакция не нарушает
равновесное распределение
Максвелла-Больмана молекул
Реагентов и продуктов по энергии
(распределение МаксвеллаБольмана сохраняется)
3. Молекулярная система считается
прореагировавшей, если она
достигла вершины потенциального
барьера реакции. Обратного
движения нет
1. A B AB
2. АК≠ находится в статистическом
равновесии с реагентами (и
продуктами). Количество
(концентрация) частиц АК≠
пропорционально числу состояний
АК≠ Количество (концентрация)
частиц реагента и продукта также
пропорционально числу состояний
реагента и продукта.
Q
AB
[AB
]
[A
]
[B
] Q
Q
A
B
3. Скорость реакции определяется
скоростью распада АК≠
k
]
AB
P r k [AB

11.

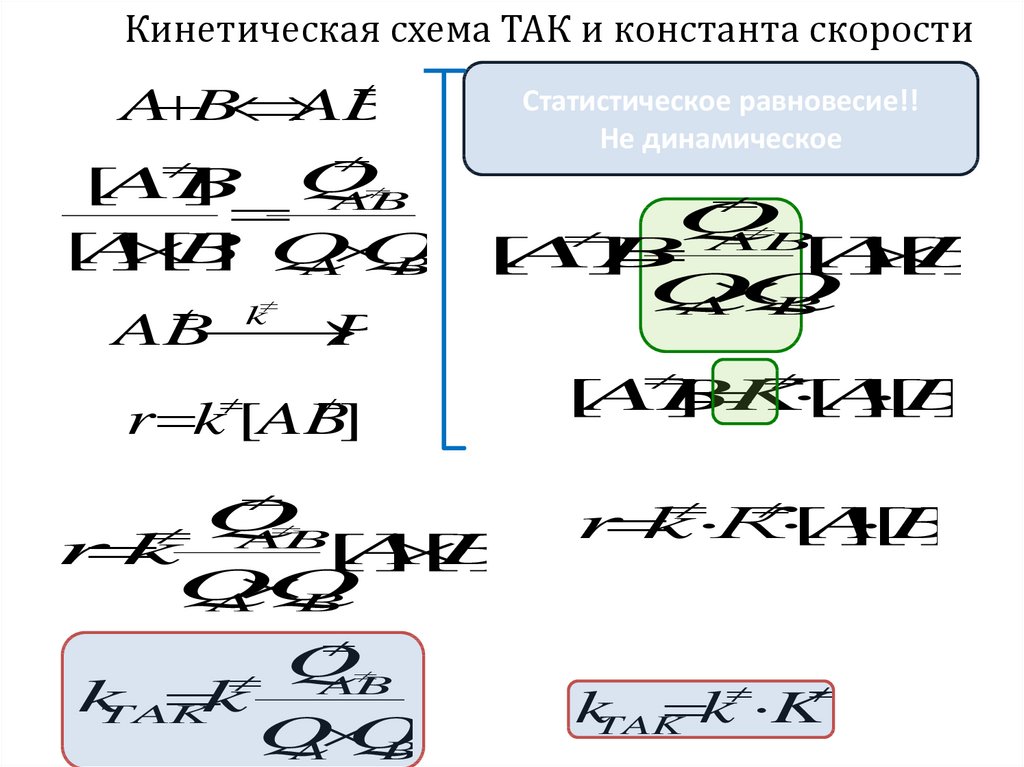
Кинетическая схема ТАК и константа скорости
A B AB
AB
Статистическое равновесие!!
Не динамическое
Q
[AB
]
Q
AB
[A
]
[B
] Q
Q
[
AB
]
[
A
]
[
B
]
A
B
Q
Q
A
B
k
AB
P
[AB
]
K [A
] [B
]
r k [AB]
AB
Q
r
k
[
A
]
[
B
]
Q
Q
A
B
Q
AB
k
k
TAK
Q
Q
A
B
r
k К [A
] [B
]
kTAK k K

12.

Вывод выражения для константы скорости ТАК
A B AB
AB
Q
[
AB
]
[
A
]
[
B
]
Q
Q
A
B
k
AB
P
r k [AB]
поступательная степень свободы по
координате реакции
(
2
m
kT
)
Q
h
t
к
.р
.
1
/2
k
k
TAK
AB
Q
Q
Q
A
B
для реакции первого порядка
k
1
1
2
2 m
k Т
Б
1
2
Т 1
k
Б
k
m
2

13.

Вывод выражения для константы скорости ТАК
k
k
TAK
AB
Q
Q
Q
A
B
Т 1
(
2
m
kT
)
k
Б
Q
k
h
m
2
t
к
.р
.
1
/2
1
2
1
/
2
Б
TAK
AB
k
T
(
2
m
kT
) Q
1
k
2
m
h Q
Q
A
B
Q
k
T AB
Б
k
TAK
hQ
Q
A
B
kБT
kTAK
K
h

14.

Условное представление АК≠.
Истинная энергия активации
1
E
h
i
2в се
E
0
AK
E0(→
)
E0(←)
1
E
h
i
2все
0
реаг
H
0
0
Путь реакции
1
E
h
i
2все
0
прод

15.

Q
g
exp(
)
g
exp(
)
...
g
exp
)
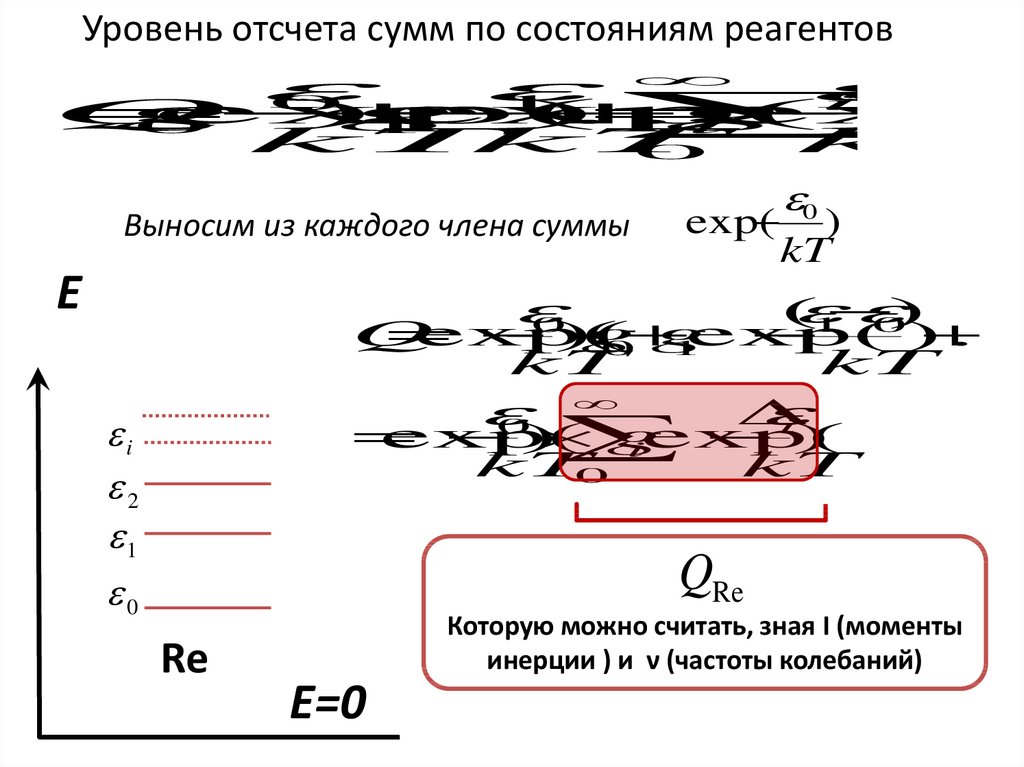
Уровень отсчета сумм по состояниям реагентов
0
0
i
1
1
i
0
kT
kT
Выносим из каждого члена суммы
exp(
kT
0
)
kT
(
)
0
1
0
Q
exp(
)(
g
g
exp(
)
...
E
0
kT
1
kT
0
i
exp(
)
g
exp(
)
i
kT
kT
i
2
1
0
0
QRe
Re
Которую можно считать, зная I (моменты
инерции ) и ν (частоты колебаний)
E=0

16.

Уровень отсчета сумм по состояниям
i
Q
g
exp(
)
..
g
exp(
)...
0
0
i
kT
i
kT
exp(
Выносим из каждого члена суммы
i
E
i
2
1
0
1
0
АК≠
E0/NA
0
)
kT
Q
exp(
0)(
g
..
g
exp(
i ).
0
kT
i
exp(
0) g
exp(
i)
kT
0
i
Q
kT
kT
AK
Которую можно считать, зная I≠ (моменты
инерции ) и ν ≠ (частоты колебаний)
Re
E=0
0 E/
0 N
A
0

17.

Расчет kТАК
Q
exp(
)
AB
0
k
T
kT
Б
k
TAK
h{
0
Q
Q
}
exp(
)
A
B
kT
0 E/
0 N
A
0
AB
E
k
TQ
0
Б
k
exp(
)
TAK
h
{
Q
Q
}
RT
A
B

18.

Неадиабатический переход (случается)
1ое возбужденное состояние
Переход есть!
основное состояние
Система переходит с одной энергетической кривой (ППЭ)
на другую, если кривые (ППЭ) пересекаются.
Электронное состояние системы меняется

19.

Туннелирование в реакциях многоатомных
молекул
прохождение системы из одной долины в другую,
“просачиваясь” мимо потенциального барьера
(чаще всего протон, идут при низких температурах)
внутримолекулярный
туннельный перенос
атома водорода в
малоновом альдегиде
CH
CH
OH
CH
OH
,
T
4
K
3
3
4CH
2
перенос протона

20.

Учет возможности туннелирования и
неадиабатических переходов
AB
Q
E
k
T
0
Б
k
exp(
)
TAK
h
Q
Q
RT
A
B
1
1
трансмиссионный коэффициент
если случается туннелирование
если случаются неадиабатические переходы

21.

Расчет kТАК
Нелинейный комплекс
Q
E
k
T
Q Q
Q
Q
0
Б
AB
t
v
rot
k
exp(
)
TAK
h
Q
Q
RT
A
B
(2
mkT
)3/2
Q
t
3
h
Все массы известны. Особенность –
объем V не водит в выражение
поступательной суммы по состояниям,
т.к выражение получено из константы
равновесия К (статистический вариант)
2 3
3
/
2
3
/
2
8
(
8I
I
I
)
(
kT
)
X
Y
Z
Q
r
3
h
3
N
7
Все моменты инерции
известны
1
h
Все частоты колебаний
Q
,
V
X
известны
k
X
1
exp(
)
T

22.

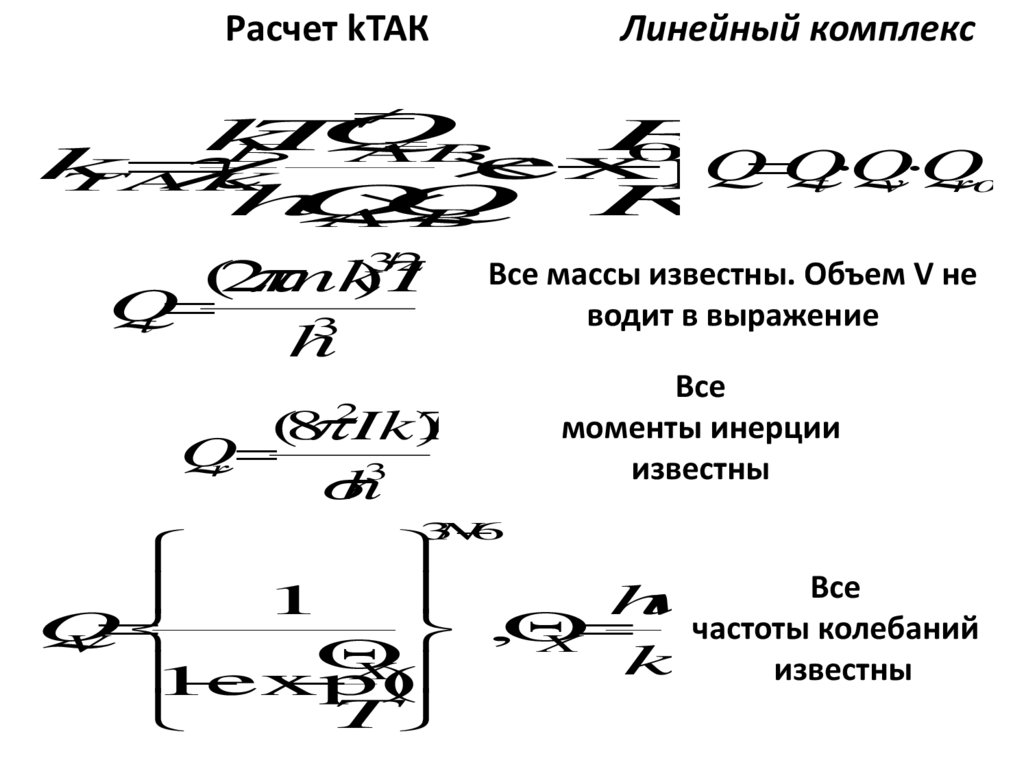
Расчет kТАК
Линейный комплекс
AB
Q
E
k
T
0
Б
k
exp(
)Q Q
TAK
t Q
v Q
rot
h
Q
Q
RT
A
B
(2
mkT
)
Q
t
3
h
3/2
Все массы известны. Объем V не
водит в выражение
(8
IkT
)
Q
r
h3
2
3
N
6
Все
моменты инерции
известны
Все
1
h
частоты колебаний
Q
,
V
X
k
X
известны
1
exp(
)
T

23.

Расчет kТАК
Q
E
k
TAB
0
Б
k
exp(
)
TAK
h
Q
Q
RT
A
B
После расчета ППЭ известны
E
(
q
,q
,q
..
q
)
- координаты минимумов
и седловой
точки
полная
1
2
3
3
N
6
Теория
- высота барьера для перехода от реагентов
активированного
к продуктам
- вторые
частные производные
Е’’
комплекса
– теория
Геометрия реагентов и АК≠ дает возможность
абсолютных
рассчитать моменты инерции, а вторые
скоростей
частные производные
- частоты колебаний.
Таким образом, есть возможность получить

24.

AFw
Определите энергию активации мономолекулярной реакции, если частота колебаний по разраваемой связи 2,4 1013 с-1, экспериментальное
значение константы скорости при 1000 К k=510 мин-1, трансмисионный коэффициент 0,8