Similar presentations:
Растворы электролитов
1.
Растворы электролитовПропускание тока через раствор электролита сопровождается разложением растворенного вещества и
выделением его составляющих (или их продуктов) на электродах. Т.о. движение заряда в таком
растворе сопровождается движением атомов или групп атомов – частей растворенного вещества.
Выделение происходит на обоих электродах, в эквивалентных количествах.
Законы Фарадея
1
2
m kIt
k
1 A
F n
n
It m Q m F
A
Ag
H
Cu
Zn
A.м.(г)
108
1
64
65
1/F=1.037 10-5 г/к,
k (мг/к)
1.118
0.01
0.32
0.34
F=96500 к
Если пропустить 1 F электричества, то выделяется
m=(A.м.)/n вещества
Элементарный электрический заряд:
наименьшее количество электричества,
существующее в природе (Гельмгольц)
e
F
96500
1.60 10 19 K
23
N 6.02 10
1
2.
ЭлектролитыЭлектролиты
Сильные
Ионный кристалл
U
+
+
Потенциал Леннарда-Джонса
-
+
-
Истинные
Ионные кристаллы:
NaCl, NH4NO3
Слабые
I J
U or
+
-
U w a R12 b R 6
Потенциальные
Молекулы, дающие
ионы в результате
взаимодействия с
растворителем:
HCl, CO2, NH3,
CH3COOH
R
σ
d
I J J I
2
σ – диаметр частицы,
d – равновесное расстояние,
a – параметр отталкивания,
b – параметр притяжения
Энергия кристалла из N катионов и N анионов:
kTR6
U ind
U disp
2
R6
3 II IJ I J
2 I I I J R6
U N az1 R n e 2 R
z1 – число ионов в 1-й координационной сфере, α – постоянная решетки (постоянная Маделунга,
для NaCl α = 1.748), e – элементарный заряд
2
3.
Растворение ионного кристалла в водеH
+
-
H
-
H
-
+
+
+
H
O
-
O
+
H
O
H
-
+
-
-
+
+
Почему электролиты диссоциируют в растворе ?
O
Закон Кулона:
q1q 2
F k 2
R
O
H
Растворитель
Вода
Нитробензол
Метилэтилкетон
Пиридин
Анилин
ε
(C2H5)2NH2Pi
78.3
99
34.5
45
17.8
61
12.5
72
7
5
N
H
(C2H5)2NH2Cl
KPi
94
100
3
74
6
85
5
58
2
нет данных
O
N
O
O
N
O
Степень диссоциации (%) 0.5 мМ растворов солей в различных
растворителях (по книге Измайлова “Электрохимия растворов”)
O-
O
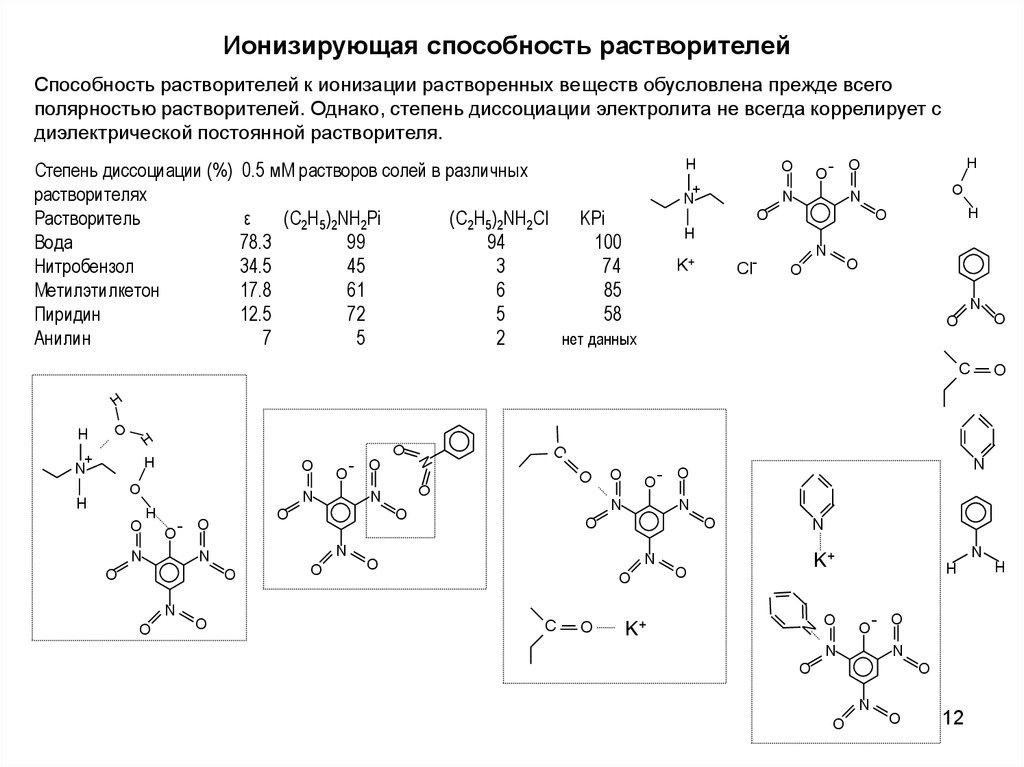
Пикраты сильно диссоцииованы,
начиная с
ε > 10, а хлоридная соль слабо
диссоциирована даже в нитробензоле.
Зависимость степени диссоциации от ε
не всегда монотонна
3
4. Вывод законов Фарадея из представлений о ионах
1m kIt
2
k
1 A
F z
1+2
m
1 A
It
F z
Масса выделившегося вещества ? – массе одной частицы, умноженной на число частиц:
m m1n
A
m1
N
Масса одной частицы:
Итак,
A
m n
N
Произведение силы тока на время – это величина перенесенного заряда, т.е.
произведение элементарного заряда, заряда (валентности) иона и числа
It Q ezn
перенесенных частиц:
F
It Q ezn zn
N
N
N
It
→ n Q
zF
zF
Получим объединенный закон Фарадея:
m
A N
1 A
It
It
N zF F z
4
5.
Гидратация и сольватация ионов в растворах электролитовРастворение электролитов, как правило, экзотермический процесс, тогда как получение
ионов в газовой фазе требует очень больших затрат энергии.
Отсюда – представления о гидратации и сольватации: образованием каких-то связей
между ионами и молекулами растворителя, что и делает этот процесс энергетически
выгодным
Пример:
+ 2Cl-, aq ΔH= -50 кДж/моль
CuCl2cr
Cu2+,
aq
CuCl2cr
Cu2+,
gas
+ 2Cl-, gas ΔH= +1986 кДж/моль
Гидратация катионов – взаимодействие с неподеленными электронными парами кислорода в
молекуле воды. Катионы s и p элементов – ион-дипольное взаимодействие, катионы переходных
металлов – донорно-акцепторная связь за счет перехода электронов атома кислорода на вакантные
связывающие орбитали катионов металлов.
Гидратация анионов – за счет образования водородных связей с частичным переходом электронной
плотности с аниона на молекулу воды.
Сольватация: катионы взаимодействуют с донорными функциональными группами или атомами
растворителей, а анионы – с акцепторными. Соответственно, основные (по Льюису) растворители
склонны сольватировать катионы, а кислотные – анионы.
5
6.
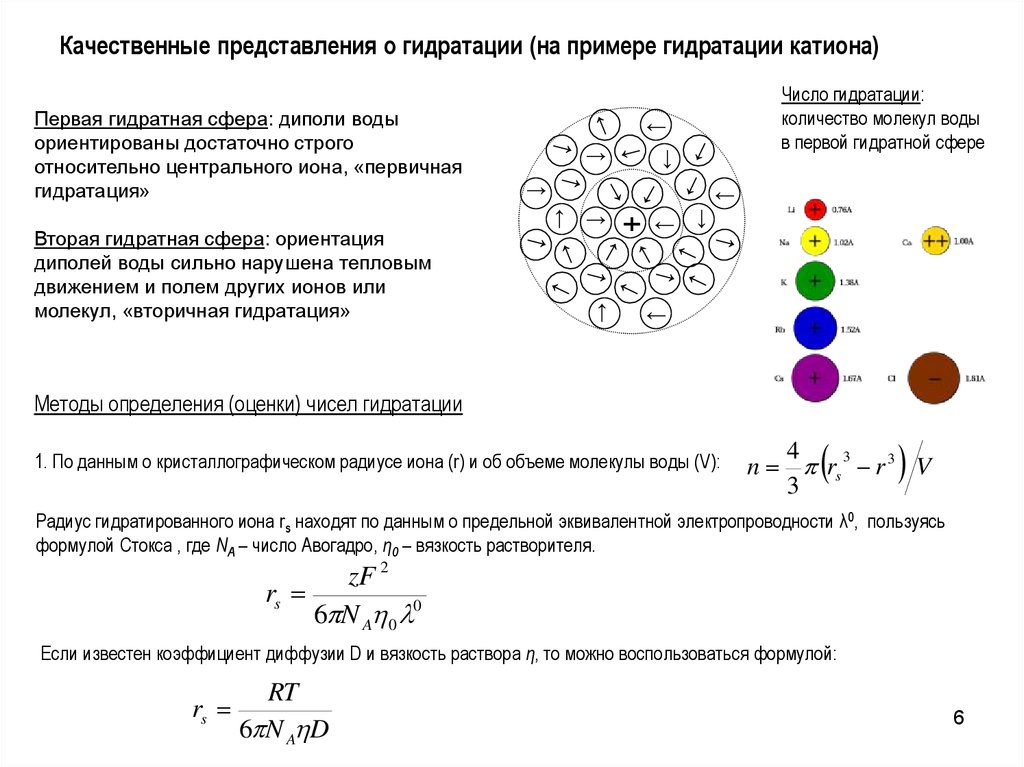
Качественные представления о гидратации (на примере гидратации катиона)←
+
←
←
←
←
←
←
←
Вторая гидратная сфера: ориентация
диполей воды сильно нарушена тепловым
движением и полем других ионов или
молекул, «вторичная гидратация»
←
←
Первая гидратная сфера: диполи воды
ориентированы достаточно строго
относительно центрального иона, «первичная
гидратация»
Число гидратации:
количество молекул воды
в первой гидратной сфере
←
Методы определения (оценки) чисел гидратации
1. По данным о кристаллографическом радиусе иона (r) и об объеме молекулы воды (V):
4
3
n rs r 3 V
3
Радиус гидратированного иона rs находят по данным о предельной эквивалентной электропроводности λ0, пользуясь
формулой Стокса , где NA – число Авогадро, η0 – вязкость растворителя.
zF 2
rs
6 N A 0 0
Если известен коэффициент диффузии D и вязкость раствора η, то можно воспользоваться формулой:
rs
RT
6 N A D
6
7.
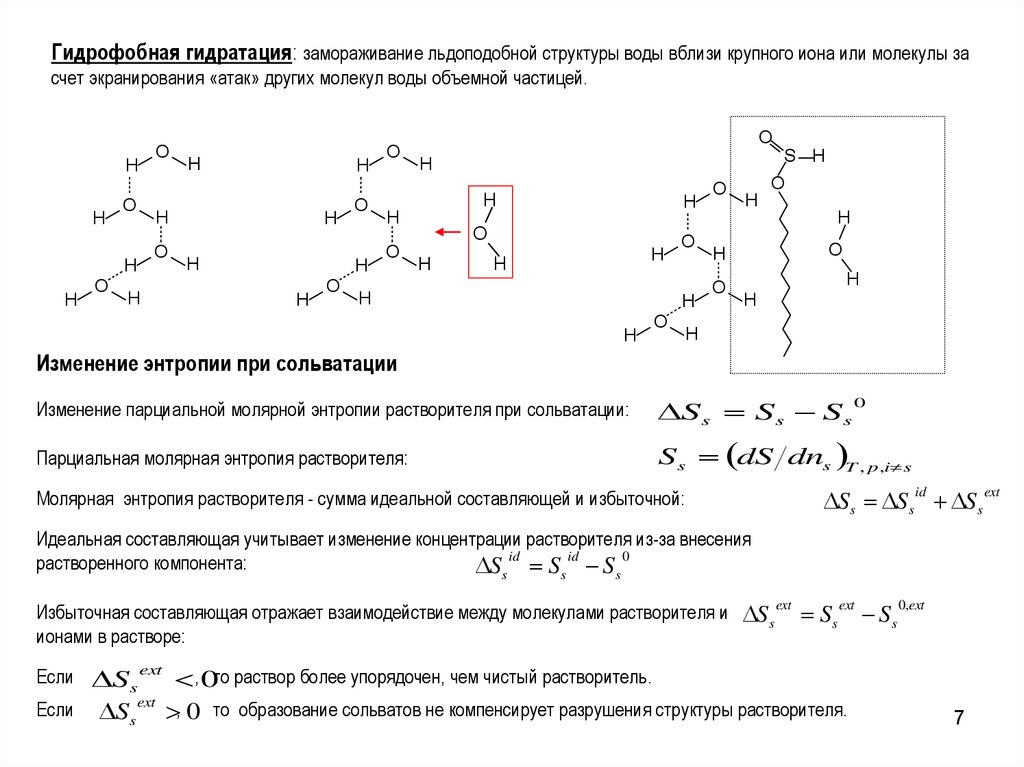
Гидрофобная гидратация: замораживание льдоподобной структуры воды вблизи крупного иона или молекулы засчет экранирования «атак» других молекул воды объемной частицей.
H
H
O
H
H
O
H
O
H
H
H
O
H
H
O
H
H
O
O
O
S H
H
H
H
O
H
O
H
H
H
H
O
H
H
O
O
O
H
H
O
H
O
H
H
H
Изменение энтропии при сольватации
Изменение парциальной молярной энтропии растворителя при сольватации:
Ss S s S s
Парциальная молярная энтропия растворителя:
Ss dS dns T , p ,i s
Молярная энтропия растворителя - сумма идеальной составляющей и избыточной:
0
Ss Ss Ss
id
Идеальная составляющая учитывает изменение концентрации растворителя из-за внесения
id
id
0
растворенного компонента:
Ss Ss Ss
Избыточная составляющая отражает взаимодействие между молекулами растворителя и Ss ext Ss ext Ss 0,ext
ионами в растворе:
Если S s ext , 0то раствор более упорядочен, чем чистый растворитель.
Если Ss ext , 0 то образование сольватов не компенсирует разрушения структуры растворителя.
7
ext
8.
Оценка ионных составляющих свободной энергии и энтальпии сольватацииВ конденсированных системах при комнатной температуре различие между значениями ΔG и ΔH невелико.
Поэтому
G H
H
s
dissolv
cryst
Строго разделить ΔG и ΔH сольватации электролита на ионные составляющие невозможно. Предполагают,
что эти величины одинаковы у гидратов одинаковых радиусов. К этому условию приближается CsI
ΔHs, CsI = -560.4 кДж/моль, принимая ΔHs, Cs = ΔHs, I , для каждого из ионов получим 280.2
кДж/моль.
Далее, для солей CsX считаем ΔHs, X = ΔHs, CsX – ΔHs, Cs , а для иодидов MI ΔHs, M = ΔHs,CsI –
ΔHs, I .
Так получают шкалу ионных энтальпий и свободных энергий гидратации для всех солей
цезия и всех иодидов, а затем – вообще для любых электролитов.
Слабости этого подхода:
1.
Сравнительно произвольный, хотя и логичный выбор «пилотного» электролита – CsI;
2.
Допущение, что термодинамические функции гидратации пилотных ионов не зависят от
природы другого иона в электролите, т.е. гидратация Cs+ одна и та же в растворах всех
солей цезия, а гидратация I- - во растворах всех иодидов.
Для каких растворов справедливо допущение 2?
8
9.
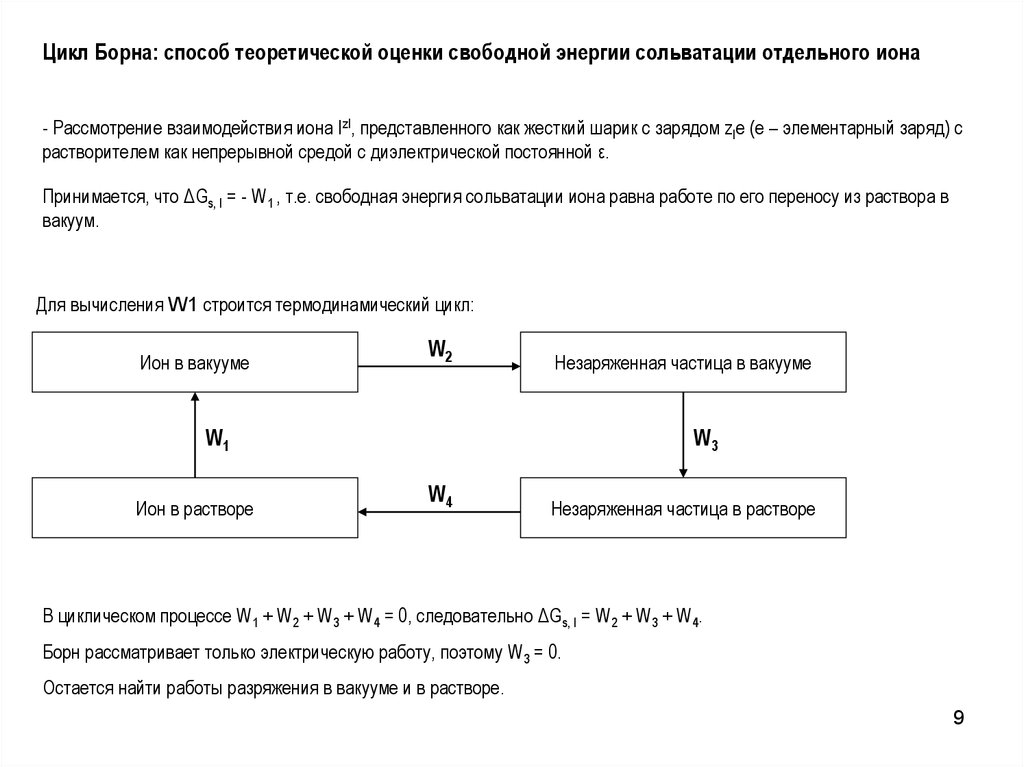
Цикл Борна: способ теоретической оценки свободной энергии сольватации отдельного иона- Рассмотрение взаимодействия иона IzI, представленного как жесткий шарик с зарядом zIe (e – элементарный заряд) с
растворителем как непрерывной средой с диэлектрической постоянной ε.
Принимается, что ΔGs, I = - W1 , т.е. свободная энергия сольватации иона равна работе по его переносу из раствора в
вакуум.
Для вычисления W1 строится термодинамический цикл:
Ион в вакууме
W2
Незаряженная частица в вакууме
W1
Ион в растворе
W3
W4
Незаряженная частица в растворе
В циклическом процессе W1 + W2 + W3 + W4 = 0, следовательно ΔGs, I = W2 + W3 + W4.
Борн рассматривает только электрическую работу, поэтому W3 = 0.
Остается найти работы разряжения в вакууме и в растворе.
9
10.
Цикл Борна- продолжениеРабота разряжения 1 моля ионов в вакууме определяется электростатическим потенциалом ΦR , зарядом на
поверхности иона q и диэлектрической постоянной среды (вакуума) – ε0:
zI e
zI e
W2 N A RI dq N A
q
4 0 RI
0
0
dq N A
zI e 2
8 0 RI
Работа разряжения 1 моля ионов в среде растворителя - аналогично:
zI e
zI e
0
0
W4 N A RI dq N A
Комбинируя, получим Уравнение Борна для свободной энергии
сольватации:
Дифференцируя по температуре, получим
выражение для энтропии сольватации:
S s ,I
d Gs ,I
dT
q
4 0 RI
Gs ,I N A
dq N A
zI e 2
8 0 RI
z I e 2
1
1
8 0 RI
z e 1 d
N A I
2
8
R
dT
p
p
0 I
2
Пользуясь уравнением Гиббса-Гельмгольца, получим для энтальпии сольватации Уравнение Борна-Бьеррума:
G H
G
T
T p
H s , I Gs , I T S s , I p N A
z I e 2
1
1 d
1
T
8 0 RI
2 dT p
10
11.
Классификации растворителейПротонные - отделяют или присоединяют H+ :
R-OH, R2-NH, R-SH
Апротонные – не отделяют и не присоединяют
H+ : C6H13, C6H6, CCl4
Кислые – склонны отдавать H+ : CH3COOH,
др. кислоты
Жесткие – лучше взаимодействуют с
жесткими (слабо поляризуемыми)
ионами, гл. обр. электростатика: H2O
хорошо гидратирует H+, Li+, Mg2+, SO42-
Основные – склонны присоединять H+ :
NH3, пиридин
Мягкие – лучше взаимодействуют с
мягкими (хорошо поляризуемыми)
ионами, гл. обр. ковалентные связи
Амфотерные: H2O, спирты, фенолы
Растворители
Нивелирующие - сближают электролиты по их
способности к диссоциации (по сравнению с
H2O), например R-OH нивелируют силу кислот
Дифференцирующие – усиливают различия
электролитов по их способности к
диссоциации, например кетоны
дифференцируют силу кислот
11
12.
Ионизирующая способность растворителейСпособность растворителей к ионизации растворенных веществ обусловлена прежде всего
полярностью растворителей. Однако, степень диссоциации электролита не всегда коррелирует с
диэлектрической постоянной растворителя.
Степень диссоциации (%)
растворителях
Растворитель
Вода
Нитробензол
Метилэтилкетон
Пиридин
Анилин
0.5 мМ растворов солей в различных
ε
(C2H5)2NH2Pi
78.3
99
34.5
45
17.8
61
12.5
72
7
5
(C2H5)2NH2Cl
KPi
94
100
3
74
6
85
5
58
2
нет данных
H
O
+
N
N
O-
H
O
O
N
O
H
O
H
Cl-
K+
N
O
O
N
O
O
C
O
H
O-
N
N
O
N
O
O
O-
O
N
O
N
N
O
O
N
O
O
O
O
O-
O
O
H
O
N
O
H
C
O
H
H
+
N
N
O
O
N
O
O
C
O
N
O
K+
N
N
K+
O
N
O
H
O
H
O-
N
O
N
O
O
N
O
O
12
H
13.
Активность и концентрация компонентаФормальное соотношение активности и концентрации:
ai Ci γ i
Концентрация – величина, пропорциональная количеству вещества в единице
массы или объема, в этом смысле – относительна, но абсолютна в том смысле, что
не является разностной. Концентрация имеет размерность.
Активность – величина, связанная со свободной энергией и заданная как функция
химического потенциала:
i i0 RT ln ai / ai 0 i0 RT ln ai
ai ai0 exp i i0 RT
Поэтому численное значение активности зависит от выбора стандартного
состояния. Активность – безразмерная величина, размерность коэффициента
активности обратна размерности концентрации:
C 1
13
14.
Особенности термодинамики ионных системПолные потенциалы – потенциалы, которые включают все виды работы,
совершаемой при перемещении массы компонента из одной части системы в другую
Примеры:
Гравитационно-химический потенциал. Пусть масса i-го компонента dni
перемещается вдоль вертикальной оси (т.е. вдоль градиента поля тяготения) на
расстояние (h”–h’). Изменение свободной энергии Гиббса составит
dG=(μi”- μi’)dni + Mig(h”-h’)dni. πi = μi + Migh (химическая + механическая работа)
Mi – масса, соответствующая dni, g –ускорение свободного падения.
Равновесие устанавливается при dG=0, т.е. πi’= πi” или μi’+Migh’= μi”+Migh”
Электрохимический потенциал. Пусть dni ионов сорта i преодолевает скачок
электрического потенциала (ψ”- ψ’). Изменение свободной энергии Гиббса составит
dG = (μi”- μi’)dni + ziF(ψ”- ψ’)dni. μ
I=
μi+ziFψ (химическая и электрическая работа)
Равновесие устанавливается при dG=0, т.е.
или i ' i " , т.е.
dG i ' i " dni zi F ' " 0
i / zi F / i " zi F "
14
15.
Активность электролита, средние и ионные активностиν M z ν- X z
Пусть электролит диссоциирует по схеме: M X
Раствор: растворитель S и растворенный электролита E. Запишем для них уравнение
Гиббса-Дюгема: n d n d 0 или n d ln a n d ln a 0
s
s
e
e
s
s
e
e
С другой стороны, раствор состоит из растворителя и ионов. Для раствора в 1000 г
1000
растворителя можем записать:
d s m d m d 0
1000
M
s
d ln as m d ln a m d ln a 0
или
Ms
1000
d ln as me d ln ae 0
Ms
m d ln a m d ln a me d ln ae
Моляльные концентрации ионов: m me
m me
a
a
0 или
Следовательно, d ln a d ln a d ln ae 0 т.е. d ln
ae
lim a m me lim a m me
Стандартное состояние:
me 0
Const
me 0
Для электролита стандартное состояние выбираем так, чтобы Const=1:
Отсюда связь активности электролита,
средней активности и активностей ионов:
a a
ae
1 /
e
a a
Коэффициент активности электролита и ионные
коэффициенты активности
a m
a a
1 /
1 /
a a ae
ν ν ν
15
16.
Методы экспериментального определения коэффициентов активности1. Методы, использующие данные о химическом потенциале растворителя
(например -давлении пара) - основаны на уравнении Гиббса-Дюгема
ni d i 0
i
1.1. Давление пара растворителя над раствором
0
as ps ps
пропорционально активности растворителя:
1.2. Изопиестический метод: два раствора нелетучих
компонентов приводят в равновесие по
растворителю, затем определяют составы обоих
растворов.
1.3. Криоскопический и эбуллиоскопический методы: по изменению температуры
замерзания или кипения в сравнении с чистым растворителем
16
17.
2. “Прямые” методы2.1. Экстракционный метод: μi(1) = μi(2) – приводят в равновесие
растворы в двух несмешивающихся растворителях.
Находят коэффициент распределения ki = Ci(1)/Ci(2) при разных
значений концентраций.
ki
Экстраполируя на предельное разбавление, находят ki0 –
термодинамический коэффициент распределения, ki0 = ai(1)/ai(2)
ki0
Ci(2)
Зная
и активности компонента в одном из растворителей, можно
теперь найти их для другого растворителя.
0
(1)
( 2) 0
( 2) ( 2) 0
0
ai
ai ki
Ci i ki
(1)
( 2 ) ki
i (1) 2
i
2
ki
Ci
Ci ki
Ci ki
2.2. Метод э.д.с.: определяем активность электролита IX в растворе, путем
измерения разности потенциалов 2-х электродов, обратимых, соответственно, к
RT
RT
ионам I+ и X0
0
k i0
i i
F
x x
ln ai
ln a x
F
RT
2 RT
E i x E 0
ln ai a x E 0
ln a ix
F
F
Проблема: все экспериментальные методы дают активность компонента (электролита
как целого). Строгих методов измерения активности ионов не существует.
Приближение Мак-Иннеса: a KCl aK aCl aK aCl aK aCl
Приближение Гуггенгейма: a CaCl a a
2
3
2
Ca Cl
aCa aCl a a
3
2
Ca Cl
aNa
NaCl
a
a
NaCl 2
NaCl
NaCl
Cl
a
концентрации
растворов одинаковы
NaCl 2
NaCl
a KCl
17
KCl
18.
Теория сильных электролитовСильный электролит: вещество, которое полностью диссоциирует при любой его
концентрации в растворе
Экспериментальные факты в пользу существования сильных электролитов
1. По данным рентгеноструктурного анализа кристаллическая решетка сильного электролита
построена из ионов. Если молекулы отсутствуют в кристалле, то тем менее вероятно их
появление в растворе, где силы притяжения между ионами уменьшаются в силу высокой
диэлектрической проницаемости среды
2. Коэффициенты экстинкции растворов сильных электролитов не зависят от концентрации
3. Молярные теплоты нейтрализации сильных кислот и оснований не зависят от концентрации
Термодинамика описывает свойства физико-химических систем с помощью параметров
состояния и функций состояния. Некоторые из них можно измерить непосредственно, другие
– выразить через измеримые величины изменения в ходе какого-либо процесса.
Термодинамика не дает возможности описать эти величины с помощью модельных
представлений.
В частности, получить теоретически связь между коэффициентами активности и составом
раствора можно только из внетермодинамических представлений.
18
19.
Задача: найти способ теоретического расчета электролитных (и ионных !)коэффициентов активности
Если нас интересует активность, обратимся к величине химического потенциала.
Разность химических потенциалов компонента в интересующем нас состоянии и в стандартном
состоянии разобьем на “идеальную” часть и “поправку”
i i 0 i RT ln Ci RT ln i i ,id i ,corr
Перейдем к соответствующим выражениям для свободной энергии Гиббса:
d Gid
i ,id
dn
i T , p ,n j i
d Gcorr
i ,corr
dn
i
T , p ,n j i
d Gcorr
RT ln i
dn
i
T , p , n j i
Итак, надо найти выражение для величины ΔGcorr
Теория Дебая-Хюккеля
Исходные положения:
1. Неидеальность вызвана межчастичными взаимодействиями: ориентационным, индукционным,
дисперсионным, а также кулоновским межионным взаимодействием
2. Все перечисленные взаимодействия, кроме кулоновского, заметны на расстояниях в пределах
1 нм, на расстояниях 10 нм и более кулоновское взаимодействие – единственное. (1 моль/л – 1
нм, 10-3 моль/л -10 нм)
Таким образом, мы можем ограничиться рассмотрением только кулоновских взаимодействий, но
должны быть готовы к тому, что теория не будет работать при концентрациях свыше 10-3 моль/л
19
20.
Ищем выражение для “поправочного” слагаемого свободной энергии – ΔGcorr,рассматривая только кулоновское взаимодействие
Стандартное состояние – идеальный предельно разбавленный раствор. В нем нет межионных
взаимодействий. При увеличении концентрации электролита ионы сближаются и начинают
взаимодействовать. Непосредственное вычисление соответствующего изменения свободной
энергии невозможно. Но можно заменить реальный процесс подходящим циклом, причем в нем
будет рассматриваться только электрическая работа.
Ион в вакууме
W
Незаряженная
частица в вакууме
W
Ион в растворе
W
W
Незаряженная
частица в растворе
Цикл Борна
Незаряженная частица
W1
Ион
Предельно разбавленный раствор
Незаряженная частица
W2
Ион
Раствор конкретной концентрации C
20
21.
Работа разряжения иона сорта i в предельно разбавленном раствореРазряжение – изменение заряда иона от его истинной величины zie до 0, т.е. текущее (по ходу
процесса) значение заряда q меняется от zie до 0
Для каждого значения q по ходу процесса разряжения справедливо выражение
электрического потенциала ψii, создаваемого самим ионом на расстоянии r:
i i
q
4 0 r
Электрическая работа, связанная с изменением заряда на величину dq равна
dW1 i dq
q
i
4 0 r
dq
Нас интересует именно работа разряжения данного иона, поэтому за расстояние r мы берем
радиус иона: r0. Тогда работа изменения заряда от zie до 0 равна
0
0
W1 i dq
i
zi e
zi e
q
4 0 r0
dq
zi e 2
8 0 r0
21
22.
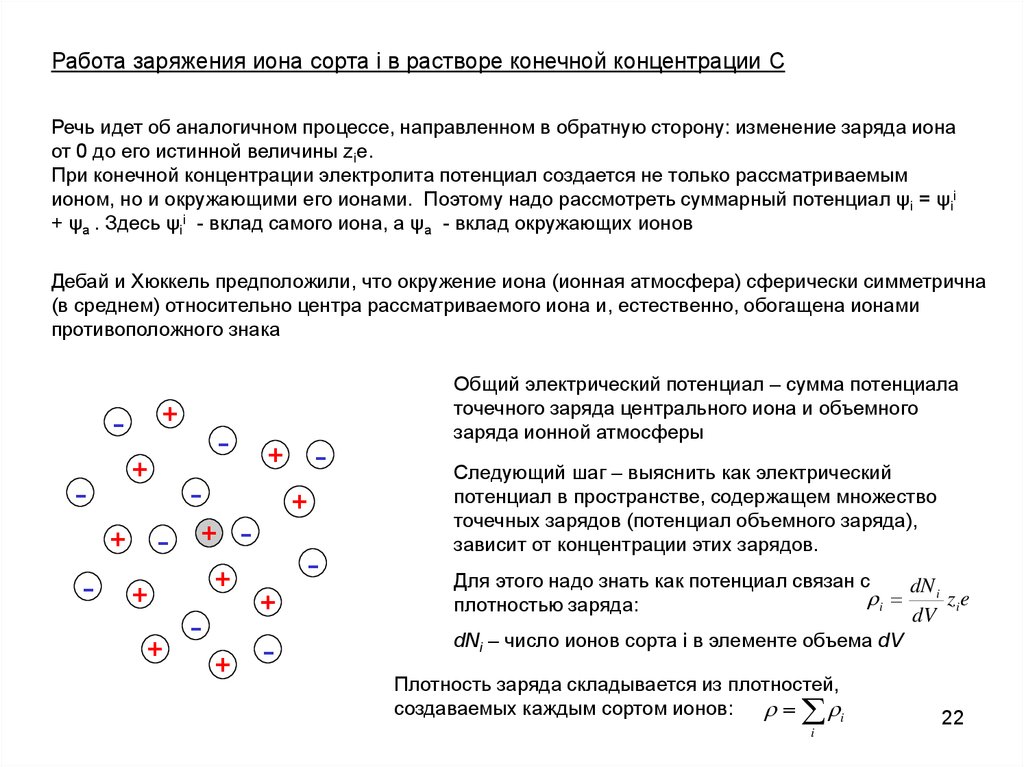
Работа заряжения иона сорта i в растворе конечной концентрации CРечь идет об аналогичном процессе, направленном в обратную сторону: изменение заряда иона
от 0 до его истинной величины zie.
При конечной концентрации электролита потенциал создается не только рассматриваемым
ионом, но и окружающими его ионами. Поэтому надо рассмотреть суммарный потенциал ψi = ψii
+ ψa . Здесь ψii - вклад самого иона, а ψa - вклад окружающих ионов
Дебай и Хюккель предположили, что окружение иона (ионная атмосфера) сферически симметрична
(в среднем) относительно центра рассматриваемого иона и, естественно, обогащена ионами
противоположного знака
+
+
-
-
+
+
+
+
-
+
- + -
+
-
-
+
+
-
Общий электрический потенциал – сумма потенциала
точечного заряда центрального иона и объемного
заряда ионной атмосферы
Следующий шаг – выяснить как электрический
потенциал в пространстве, содержащем множество
точечных зарядов (потенциал объемного заряда),
зависит от концентрации этих зарядов.
Для этого надо знать как потенциал связан с
dN i
i
zi e
плотностью заряда:
dV
dNi – число ионов сорта i в элементе объема dV
Плотность заряда складывается из плотностей,
создаваемых каждым сортом ионов:
i
i
22
23.
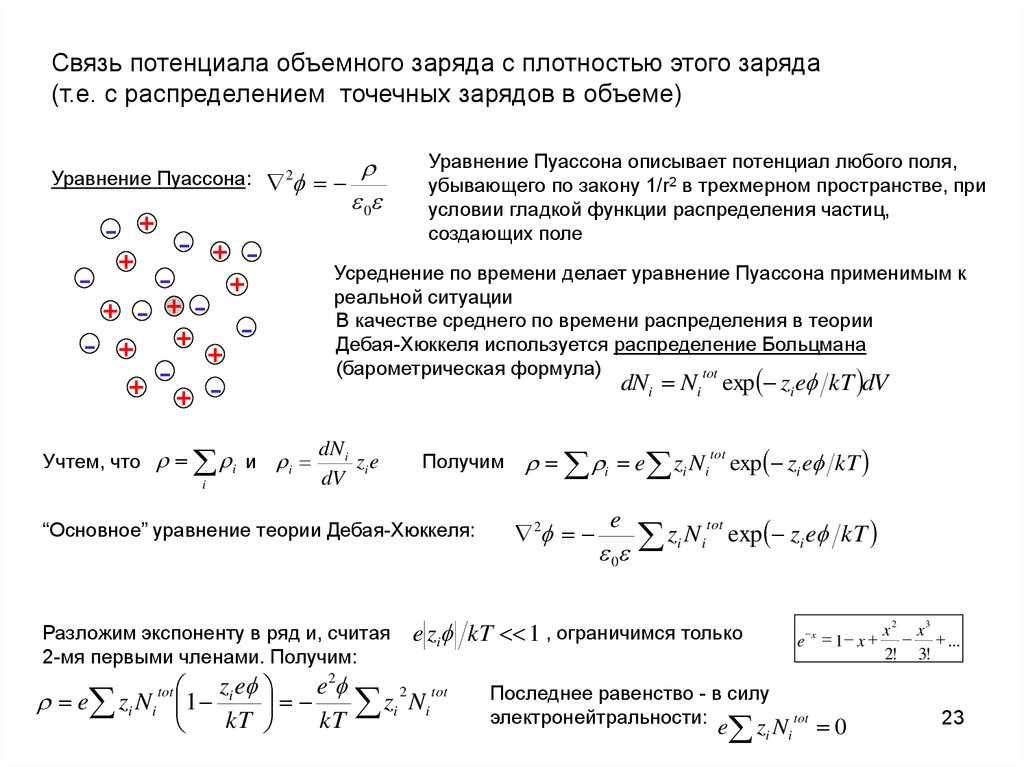
Связь потенциала объемного заряда с плотностью этого заряда(т.е. с распределением точечных зарядов в объеме)
Уравнение Пуассона:
- + + +
+
+
+ - + + + + - -
0
2
Уравнение Пуассона описывает потенциал любого поля,
убывающего по закону 1/r2 в трехмерном пространстве, при
условии гладкой функции распределения частиц,
создающих поле
Усреднение по времени делает уравнение Пуассона применимым к
реальной ситуации
В качестве среднего по времени распределения в теории
Дебая-Хюккеля используется распределение Больцмана
(барометрическая формула)
tot
dNi Ni exp zi e kT dV
+
Учтем, что
i
i
и i
dN i
zi e
dV
Получим
“Основное” уравнение теории Дебая-Хюккеля:
Разложим экспоненту в ряд и, считая
2-мя первыми членами. Получим:
2
e
0
zi Ni exp zi e kT
tot
e zi kT 1 , ограничимся только
e2
zi e
2
tot
e zi Ni 1
zi Ni
kT
kT
tot
i e zi Ni tot exp zi e kT
Последнее равенство - в силу
электронейтральности:
e zi N i
e
x
tot
2
3
1 x x x ...
2! 3!
0
23
24.
Вернемся к уравнению Пуассона, причем оператор Лапласа запишем в полярных координатах, т.к.считаем систему ион + ионная атмосфера центральносимметричной:
e2 Ni zi
d 2 2 d
2
2
dr
r dr
0
0 kT
tot
2
2
Общее решение имеет вид:
e χr
r
e χr
r
Т.е.
2 2
α и β – константы интегрирования. Ищем их
из граничных условий
На бесконечном расстоянии от иона (r → ∞ ) нет поля. Т.е. при r → ∞ д.б. ψ → 0. Первое слагаемое
при r → ∞ обращается в 0 при любых α. Чтобы вся сумма обратилась в 0 требуется β=0.
Таким образом,
e χr
r
Для определения константы α разложим и эту экспоненту в ряд, ограничиваясь 2-мя первыми
членами:
χr
2 2
e
r
r
1 r
... 1 r
r
2!
r
e2 Ni zi
tot
Поскольку
0 kT
2
, то при предельном разбавлении эта величина (χ) обращается в 0.
Соответственно, в предельно разбавленном растворе
r
.
Отсюда
ezi
4 0
24
25.
Таким образом, результирующий потенциал в системе ион – ионная атмосфера может быть записанкак
ezi
4 0 r
1 r
ezi 1
ezi 1 1
4 0 r
4
rD
0 r
rD 1
Здесь
Ионную атмосферу можно заменить зарядом, равным по величине заряду центрального иона,
противоположным ему по знаку и равномерно распределенным по сфере радиуса rD = χ-1.
Величина rD - эффективный радиус ионной атмосферы или Дебаевский радиус. Для плоского
случая (двойной электрический слой) аналог этой величины – Дебаевская длина: эффективная
толщина диффузной части двойного электрического слоя (теория Гуи-Чапмена).
e2 Ni zi
tot
Дебаевский радиус: rD
I
1
2
Ci zi
2
rD
2
2
0 kT
0 kT
2
e2 N A ni zi
tot
V 0 kT
2
e2 N A
C z 2e N I
2
2
i i
0 kT
A
0 kT
Для 1:1 электролита в воде при 25 оС
2
2e N A I
rD=2C-1/2 A, при 0.01 M – rD=20 A.
Теперь получим работу возвращения заряда на ион в растворе конечной концентрации
zie
zie
zie
zie
2
zi e2
W2 dq
dq
dq W1
qdq W1
4 0 r0
4 0 rD
4 0 rD 0
12 0 rD
0
0
0
q
q
Здесь r0 т.к. речь о заряжении иона радиусом r0
1
25
26.
Для полной электрической работы, связанной с перемещением иона сорта i из предельноразбавленного раствора в раствор конечной концентрации (т.е. работы создания ионной
атмосферы):
2 2
W W1 W2
zi e
12 0 rD
Для всех ионов электролита, присутствующих в объеме V, общая электрическая работа составит
3/ 2
e 2V Ni zi
e3 N A
We
1/ 2
12 0 rD
12 0 V 0 kT
tot
2
n z
2 3/ 2
j
j
Теперь вернемся к исходной идее: поправка на неидеальнность должна отражать только
электростатическое взаимодействие, тогда
d Gcorr
dW
RT ln i
e
dni T , p ,n j i dni T , p ,n j i
d
e NA
lg i
1/ 2
2.303RT 12 0 V 0 kT
3
3/ 2
n z
2 3/ 2
j
dni
j
1/ 2 2
3
e
N
zi I
A
3/ 2
2.303 4 2 0 kT
n j ni
1/ 2
Введем обозначение
e3 N A
A
3/ 2
2.303 4 2 0 kT
.
В водных р-рах при 25 0С А~0.509
Мы получили предельный закон (первое приближение) теории Дебая-Хюккеля:
lg i Azi
2
I
26
27.
Более точные выражения теории Дебая-ХюккеляПоправка Хюккеля: учет объема самих ионов
Интегрирование по всему объему раствора разумно проводить только тогда, когда объем,
занимаемый ионами пренебрежимо мал по сравнению с общим объемом, т.е. только для
разбавленных растворов (в пределах 0.001 М).
В более концентрированных надо иметь в виду, что ионы могут занять заметную долю объема. С
другой стороны, расстояние между центрами ионов не может быть меньше, чем сумма их радиусов.
Отсюда - второе приближение теории Дебая-Хюккеля:
Исключаем объем центрального иона, т.е. интегрируем не от 0, а от r=a. Величина a – эффективный
радиус иона (радиус Киеланда).
Тогда константа интегрирования
ezi
exp a
4 0 (1 a)
2
В результате получим
Azi I
lg i
,
1 aB I
B 2e 2 N A 0 kT .
1/ 2
В водных растворах
при 25 0С B~0.329
Значения параметра a подбирают эмпирически!
Уравнение Дэвис (3-е приближение теории Дебая-Хюккеля): учет локального изменения
диэлектрической постоянной вблизи иона (работает до 0.1 М растворов, в т.ч. CaCl2):
2
Azi I
lg i
0.1zi I
1 aB I
27
28.
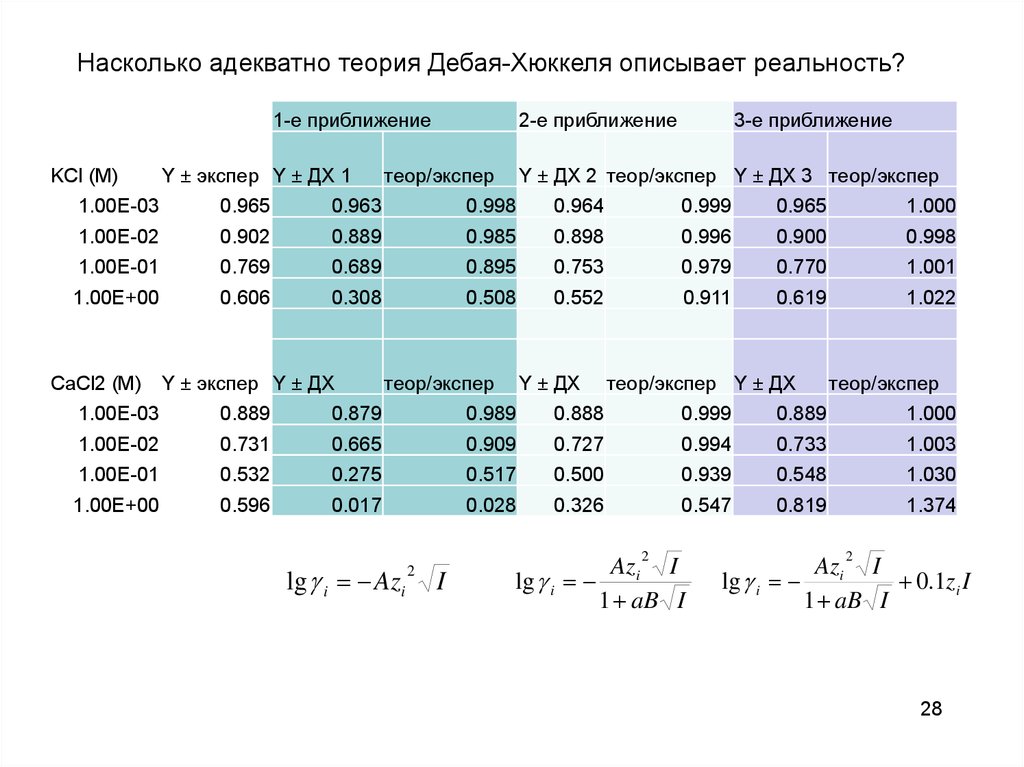
Насколько адекватно теория Дебая-Хюккеля описывает реальность?1-е приближение
KCl (M)
Υ ± экспер Υ ± ДХ 1
2-е приближение
теор/экспер
3-е приближение
Υ ± ДХ 2 теор/экспер Υ ± ДХ 3 теор/экспер
1.00E-03
0.965
0.963
0.998
0.964
0.999
0.965
1.000
1.00E-02
0.902
0.889
0.985
0.898
0.996
0.900
0.998
1.00E-01
0.769
0.689
0.895
0.753
0.979
0.770
1.001
1.00E+00
0.606
0.308
0.508
0.552
0.911
0.619
1.022
CaCl2 (M)
Υ ± экспер Υ ± ДХ
теор/экспер
Υ ± ДХ
теор/экспер Υ ± ДХ
теор/экспер
1.00E-03
0.889
0.879
0.989
0.888
0.999
0.889
1.000
1.00E-02
0.731
0.665
0.909
0.727
0.994
0.733
1.003
1.00E-01
0.532
0.275
0.517
0.500
0.939
0.548
1.030
1.00E+00
0.596
0.017
0.028
0.326
0.547
0.819
1.374
lg i Azi
2
2
I
Azi I
lg i
1 aB I
2
Azi I
lg i
0.1zi I
1 aB I
28
29.
Более современные теорииТеория Робинсона-Стокса – учет расхода растворителя на сольватацию ионов
Здесь φ – осмотический коэффициент растворителя,
s
Azi I
s hi
h
–
число
гидратации, ν – количество ионов данного
lg i
lg 1 h / ns
1 aB I 2.303ns
вида в одной молекуле электролита, ns – число
2
молей растворителя в 1-молярном растворе
электролита
Теория Питцера: ионы представлены как жесткие сферы, а не как точечные заряды. Т.е. не
просто учтен их объем, а учтено отталкивание на близких расстояниях
3/ 2
A I
2A
2
2 2
D
lg z z
ln 1 aB I m
C m
B
1 aB I
Параметры C и D эмпирические
29
30.
Перенос электрического заряда в растворах электролитовСпособы (виды) переноса: конвекция, диффузия, (электро)миграция
Конвекция: перенос объема раствора, например – из-за перемешивания
Диффузия: перенос электролита в объеме раствора под действием градиента химического
потенциала
Электромиграция: перенос электролита в объеме раствора под суммарным действием
градиентов химического потенциала и внешнего электрического поля
Сопротивление
R
l
S
Электропроводность
K R 1
Удельная электропроводность:
электропроводность объема материала
(твердого или жидкого), заключенного в
кубике с ребром 1 см, помещенном
между двумя электродами большой
площади
1S
S
l
l
Удельная
электропроводность
1 см
Вещество
Серебро
Алюминий
Уголь
NaCl (750 0C)
H2SO4 30%
KCl 1M
H2O
κ (Ом-1см-1)
6.2·105
3.6·105
2·105
3.4
0.74
9.8·10-2
5.5·10-8
30
31.
Основное понятие, применяемое при описании процессов переноса вещества, теплоты,электрического заряда, и т.д. – плотность потока. Вектор!
Плотность потока частиц сорта i: число частиц этого сорта,
пересекающих площадку единичной площади,
расположенную перпендикулярно направлению движения
частиц, за 1 единицу времени
Ji – поток частиц сорта i, двигающихся со скоростью Vi относительно системы
отсчета, которая движется со скоростью Vref
J i Ci V i V ref
Кристаллы: система отсчета – кристаллическая решетка
Растворы: разные системы отсчета
Характеристическая система Гитторфа: Vref – средняя скорость
движения частиц растворителя
J iH
Ci V i V solv
Поток в системе Гитторфа
Характеристическая система Фика: Vr = W – средняя скорость движения всего объема раствора, в
котором происходит перенос. Удобство системы Фика: если нет конвекции, т.е. раствор покоится
относительно наблюдателя, то Vref = W = 0
W Ci vi V i
i
Ci – концентрация, vi – парциальный
молярный объем частиц сорта i
J iF
Ci V i W
Поток в системе Фика
31
32.
Речь идет о движении только вдоль оси x, символвектора в дальнейшем не применяем
+
Катод
Анод
x
i F zi J i F ziC iVi FVref ziC i
Плотность электрического тока:
i
Число переноса ионов сорта i
i
FziCi Vi Vref
z C V V
I i ii S
i i i ref
I iS F ziCi Vi Vref ziCi Vi Vref
i
tiH tiF Vi Vsolv Vi W
В любой системе отсчета
t
i
i
i
i F ziC iVi
Плотность электрического тока не зависит от выбора
характеристической системы отсчета!
ti
i
i
В разбавленных растворах числа переноса по Гитторфу и по
Фику совпадают, но в концентрированных могут заметно
различаться
1
32
33.
Подвижность ионаПусть система однородна (нет градиентов) даже по
оси x. Тогда никакого направленного переноса не
будет, только хаотичное тепловое движение частиц
Наложим внешнее электрическое поле с напряженностью
x
d d x grad
f accel zi Fgrad , пропорциональная
напряженности электрического поля, и тормозящая сила трения
f inhib,t k Vi , Vsolv ,
На частицы действует постоянная ускоряющая сила
пропорциональная скорости движения частицы относительно тормозящей среды в текущий момент
времени t.
В некий момент времени t = τ достигнутая частицей скорость
порождает такую тормозящую силу, которая компенсирует
действие ускоряющей:
Vi ,
0
f accel finhib,t
dt
mi
f accel f inhib,t
k
dt Vsolv f accel zi Fgrad
mi
0
Начиная с этого момента t = τ частица движется с постоянной скоростью Vi – Vsolv = Vi,τ – Vsolv = ui
Ui ui zi F - электрическая подвижность иона IZi
Тогда для парциальной плотности тока и общей плотности тока получим
i F zi C i U i grad
i
ii F zi CiUi grad и
33
34.
Закон Ома для раствора электролита:Удельная электропроводность:
Удельное сопротивление:
F zi C i U i
i
1
i F zi C i U i grad
i
ii F zi CiUi grad
i
grad
i grad
Удельная электропроводность
и удельное сопротивление не
зависят от системы отсчета !
HCl
400
2
(Ом моль см )
Законы (правила) Кольрауша
Эквивалентная электропроводность:
C*
300
-1
C z C z C
*
-1
Эквивалентная концентрация:
200
KCl
100
1-й закон Кольрауша
0 A C
Для слабых электролитов можно записать
2-й закон Кольрауша
0 IX 0 I 0 X
(принцип независимого движения ионов)
AgNO3
CH3COOH
0
0 A C
0.0
0.1
0.2
0.3
1/2
C
Вклады ионов I+ и X- в предельную эквивалентную
электропроводность электролита IX – это величины,
характерные для данных ионов, вне зависимости от
других ионов в растворе.
Предельная эквивалентная электропроводность ионов I+ в растворе электролита IX, IY и любом
другом – одна и та же: 0 I ( IX ) 0 I ( IY )
Аналогично – для ионов X-: их вклад в проводимость растворов IX и JX один и тот же:
0 X ( IX ) 0 X ( JX )
34
35.
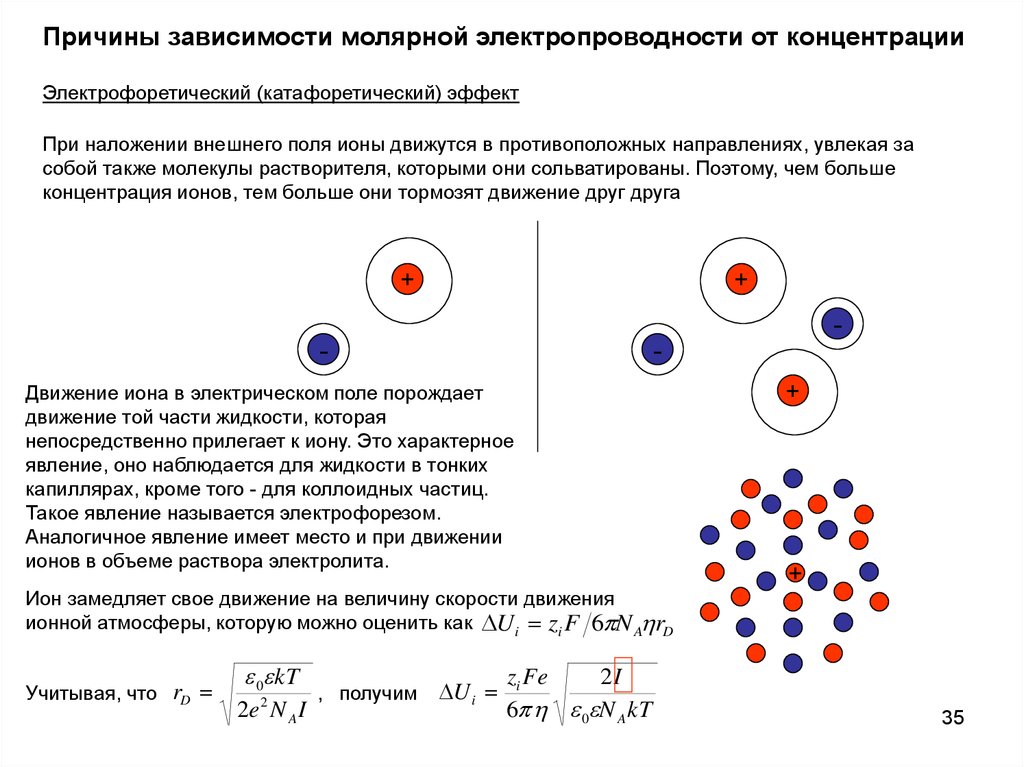
Причины зависимости молярной электропроводности от концентрацииЭлектрофоретический (катафоретический) эффект
При наложении внешнего поля ионы движутся в противоположных направлениях, увлекая за
собой также молекулы растворителя, которыми они сольватированы. Поэтому, чем больше
концентрация ионов, тем больше они тормозят движение друг друга
+
+
-
-
-
Движение иона в электрическом поле порождает
движение той части жидкости, которая
непосредственно прилегает к иону. Это характерное
явление, оно наблюдается для жидкости в тонких
капиллярах, кроме того - для коллоидных частиц.
Такое явление называется электрофорезом.
Аналогичное явление имеет место и при движении
ионов в объеме раствора электролита.
Ион замедляет свое движение на величину скорости движения
ионной атмосферы, которую можно оценить как U i zi F 6 N A rD
Учитывая, что rD
0 kT
2e 2 N A I
, получим
U i
zi Fe
2I
6 0 N A kT
+
+
35
36.
Причины зависимости молярной электропроводности от концентрацииРелаксационный эффект
Заряд ионной атмосферы
противоположен заряду центрального
иона и в среднем распределен
сферически симметрично по отношению
к центральному иону.
При наложении внешнего поля
центральный ион и ионная
атмосфера движутся в
противоположных направлениях.
+
Качественно
электрофоретический
эффект объясняет закон
Кольрауша: уменьшение
подвижности
пропорционально корню
из концентрации. Но
количественного согласия
нет, должна быть еще
какая-то причина
снижения подвижности
ионов
На некоторое время (10-9 – 10-7 с)
возникает асимметрия окружения
иона ионной атмосферой. “Старая”
ионная атмосфера (сзади по
отношению к движению иона)
разрушается, а новая – впереди –
создается.
Суммарное время разрушения старой ионной атмосферы и создания новой называется временем
2
релаксации. Это время можно оценить по формуле
, η – вязкость.
relax 6 ri rD kT
Хотя время релаксации на несколько порядков меньше, чем время, за которое ион преодолевает
расстояние, равное радиусу ионной атмосферы (10-3 с), влияние релаксации очень значительно.
Дело в том, что напряженность поля ионной атмосферы обычно превосходит напряженность
36
внешнего поля.
37.
Теория электропроводности ОнзагераТеория Онзагера учитывает межионные электростатические взаимодействия примерно также,
как они учтены в теории Дебая-Хюккеля, а потоки всех частиц описываются с помощью
уравнений гидродинамики.
Учитывается, что в результате электрофоретического эффекта подвижность иона уменьшается (по
сравнению с величиной в предельно разбавленном растворе)
Ui Ui Ui Ui zi F 6 N A rD
0
0
Кроме того, на внешнее поле Eex накладывается релаксационное поле ΔE:
В сильно разбавленном растворе одного электролита IX:
где
zz
0 0
q
i x
i
x
Если
zi z x F 2
E
q
E 12 N A 0 RT 1 q rD
,
zi z x z x i zi x 0
0
В результате Онзагер получил для эквивалентной
электропроводности выражение:
B1
E Eex E
zi z x F 3q
3 N A 2 0 RT
3/ 2
1 q
zx zi 1 и aB I 1
B2
ix ix0 B1 ix0 B2
z z F
i
x
6 N A
3
1 aBI
I
2
0 RT
, то получим закон Кольрауша:
ix ix0 B1 ix0 B2 Cix
37
38.
Эффекты Вина: увеличение электропроводности в сильных электрических полях1-й эффект Вина
В электрическом поле умеренной напряженности (E < 104 В/м) электропроводность не зависит
от величины E. В сильных полях (E ~ 107 В/м) - сильный рост эквивалентной
электропроводности, по мере увеличения напряженности поля она стремится к значению,
характерному для предельно разбавленного раствора
При высокой напряженности внешнего
электрического поля ионы движутся так
быстро, что ионная атмосфера не успевает
образоваться. В результате, как
электрофоретический, так и релаксационный
эффекты исчезают.
Граница эффекта Вина: E 4 107 C
+
В/м
2-й эффект Вина
В сильном электрическом поле увеличивается
электропроводность слабых электролитов: эффект
диссоциации в поле.
kd
Диссоциация электролита:
I+ + X-
IX
ka
Kd = kd/ka
Константа скорости ассоциации ka не изменяется при наложении поля, а константа
скорости диссоциации kd сильно увеличивается в поле. В результате равновесие
диссоциации сдвигается вправо.
38
39.
Эффект Дебая-Фалькенгагена: увеличениеэлектропроводности в переменном
электрическом поле
Исходя из идеи ионной атмосферы, Дебай и
Фалькенгаген предсказали, что эффект
асимметрии (релаксационный эффект) должен
исчезнуть, если вместо постоянного
электрического поля приложить переменное
поле высокой частоты.
+
Действительно, при частотах порядка 1 МГц,
когда период колебаний поля соизмерим со
временем релаксации
relax 6 ri rD 2 kT
наблюдается
заметное увеличение электропроводности
Даже малые (и периодические) колебания ионов вызывают
колебания их сольватных оболочек. Поэтому электрофоретический
эффект сохраняется также и в переменном электрическом поле
В переменном поле исчезает только релаксационный эффект, а электрофоретический
остается, поэтому эквивалентная электропроводность в переменном поле не достигает
значений, характерных для предельно разбавленных растворов
39
40.
Механизм переноса ионов в растворах электролитовФормула Нернста-Эйнштейна: связь коэффициента диффузии и подвижности
Формула Стокса: непрерывная диффузия
сферической частицы радиуса ri в непрерывной
среде (континууме) с вязкостью η
Di
Di U i
RT
zi F
RT
6 ri N A
Крупная частица среди маленьких!
А если размеры частиц соизмеримы, или частицы
растворителя больше, чем ионы?
Концепция Эйринга: диффузия – последовательность
скачков, для которых требуется энергия активации
2
act
kT
E
Di kli ni exp Ei
Аномальная подвижность Перенос иона из водной фазы в органическую
ионов H+ и OH- в водных
растворах
H
H
+
+
O
H
O
H
+
+
H
O
O
H
H
H
H
E
X
X
40
41.
Кислотность водных и неводных растворовШкала pH для водных растворов
Ag│AgCl, буфер, KCl (m) │H2, Pt
E E 0 Ag AgCl
RT
RT
ln aH
ln mCl Cl
F
F
F
lg mCl lg aH Cl
E E 0 Ag AgCl
2.303RT
E E 0 Ag AgCl
Буфер
Фталатный
Фосфатный
Боратный
Д-Х
4.002
6.858
9.177
γ±
4.011
6.873
9.180
RT
RT
ln aH
ln aCl Используют ГЯ без
жидкостного соединения,
F
F
чтобы избежать трудностей с
диффузионным потенциалом
Измеряют э.д.с. при разных значениях mCl и
экстраполируют на mCl = 0 (γCl = 1). По ходу
построения, γCl вычисляют по теории ДебаяХюккеля или принимают γCl = γ±KCl
Построить шкалу pH водных растворов удается только путем
внесения внетермодинамических допущений. Но результаты
внесения различных допущений оказываются очень близкими друг
к другу
Шкала pH для неводных растворов (?)
H
1
aq
2
org
aq / org
E el 2
org
H 0,aq H 0,org
F
H
aq / org
el1
org
RT aH
ln
aq
F
aH
1
aq1
2
org
aq2
aq
E el 2
aq 2
H
aq1/ org
I
Построить единую согласованную шкалу pH для разных растворителей не удается !
aq 2 / org
el1
aq1
41
42.
Функции кислотностиАррениус: кислота (HA) – вещество, которое в водном растворе отщепляет ион водорода
основание (BOH) –вещество, которое в водном растворе отщепляет ион гидроксила
HA ↔ H+ + ABOH ↔ B+ + OHБренстед: кислота (A, BH) – это вещество, способное отщеплять протон, основание (B) – это
вещество, способное присоединять протон
AzA ↔ H+ + BzA-1
BzA-1 + H+ ↔ AzA
HCl ↔ H+ + ClNH3 + H+ ↔ NH4+
Важно: необходимы 2 протолитические системы, например A1 + B2 ↔ B1 + A2
Льюис: кислота (A) – это вещество, способное быть акцептором электронов, основание (B) – это
вещество, способное быть донором электронов. Сам ион H+ - кислота Льюиса, реакции
– это вытеснение одного основания другим: AB1 + B2 ↔ AB2 + B1 По Льюису для
реакции необходимы 2 основания.
Гаммет: для сопоставления кислотности растворов в разных растворителях можно использовать
цветные индикаторы (B, BH), концентрации которых малы, поэтому внесение индикатора не
влияет на кислотность раствора.
Ka
aH aB
aBH
lg K a lg
aB
lg aH
aBH
H 0 lg K a lg
CB
lg aH lg B
CBH
BH
Функция кислотности Гаммета (нитроанилины, B, BH+)
Считается, что γB/γBH = Const для всех индикаторов во всех растворителях.
Для этого химическая структура индикаторов д.б. близкой, а концентрации - маленькими
Для индикаторов типа CH ↔ C- + H+
H lg K a lg
CC
CCH
Для индикаторов типа DH2+ ↔ D+ + H+
H lg K a lg
CD
CDH
42
43.
Расплавы солейВ расплавах в значительной мере сохраняется квазикристаллический порядок чередования
ионов различных знаков – как в кристаллической решетке.
Но в силу высокой температуры ионы в расплавах имеют высокую кинетическую энергию.
Поэтому можно предполагать высокую степень диссоциации в расплавах.
Вместе с тем, электропроводность их не так велика, как можно было бы ожидать при такой
концентрации зарядов в единице объема и высокой степени диссоциации. Электропроводность
расплавов обусловлена дефектами структуры, которых намного больше, чем в твердых солях.
Сложные закономерности чисел переноса
Удельная
электропроводность
Вещество
Серебро
NaCl (750 0C)
LiF (905 0C)
AlCl3 (200 0C)
H2SO4 30%
KCl 1M
H2O
κ (Ом-1см-1)
6.2·105
3.4
20.3
5.6·10-8
0.74
9.8·10-2
5.5·10-8
KCl – MgCl2 (1:1)
tK = 0.7, tMg = 0.14, tCl = 0.16
KCl – MgCl2 (2:1)
tK = 0.8, tMg = 0.0,
tCl = 0.20
Расплавные источники тока
Анод: металлический Li, Ca (!)
Катод: CaCrO4, CuO, Fe2O3, WO3
V ~ 3 В, i ~ 103 A/м2 (!)
LiCl - KCl
10 – 15 лет хранения в холодном
виде
43
44.
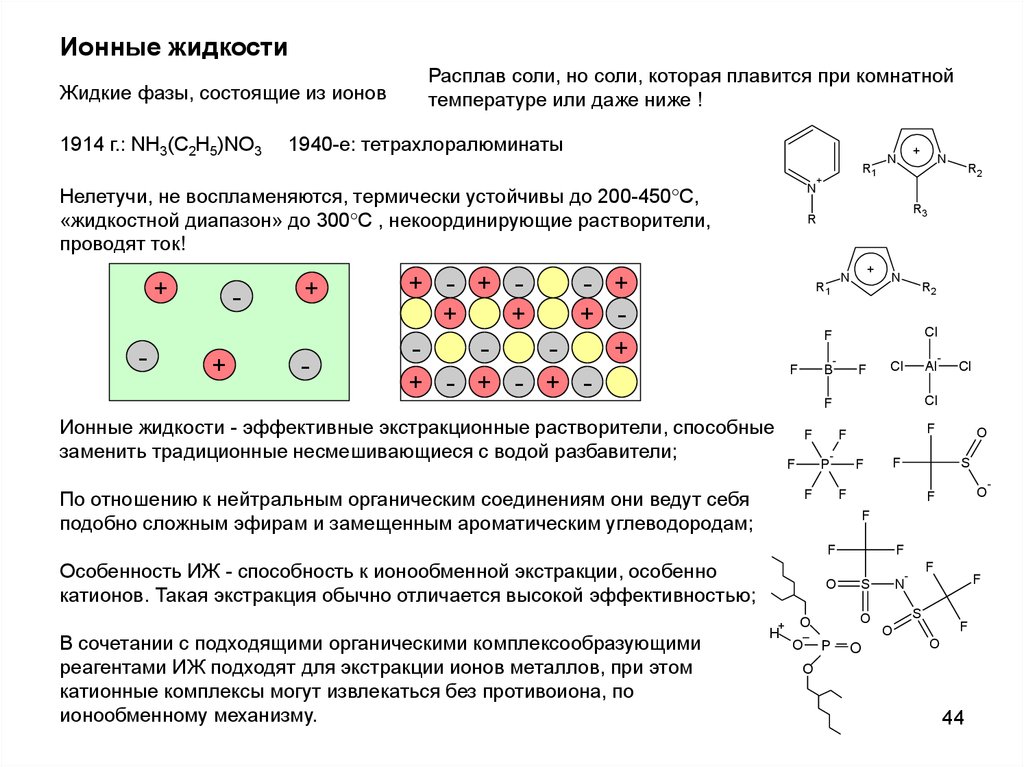
Ионные жидкостиЖидкие фазы, состоящие из ионов
1914 г.: NH3(C2H5)NO3
Расплав соли, но соли, которая плавится при комнатной
температуре или даже ниже !
1940-e: тетрахлоралюминаты
+
-
+
+
-
+
N
R2
R3
R
+ - + - +
+
+
+ +
+ - + - + -
+
N
R1
N
R2
Cl
F
F
B
-
F
Cl
Al
Ионные жидкости - эффективные экстракционные растворители, способные
заменить традиционные несмешивающиеся с водой разбавители;
F
F
По отношению к нейтральным органическим соединениям они ведут себя
подобно сложным эфирам и замещенным ароматическим углеводородам;
-
F
Cl
F
F
P
-
Cl
F
F
F
O
S
F
O
F
F
F
Особенность ИЖ - способность к ионообменной экстракции, особенно
катионов. Такая экстракция обычно отличается высокой эффективностью;
В сочетании с подходящими органическими комплексообразующими
реагентами ИЖ подходят для экстракции ионов металлов, при этом
катионные комплексы могут извлекаться без противоиона, по
ионообменному механизму.
N
N
Нелетучи, не воспламеняются, термически устойчивы до 200-450 С,
«жидкостной диапазон» до 300 С , некоординирующие растворители,
проводят ток!
+
R1
O
+
H
F
S
F
O
_
O
F
N
O
O
F
-
S
P
O
O
O
44
-


































 chemistry
chemistry








