ДУ и численные методы. Системы дифференциальных уравнений. 2 семестр. Лекция 8

1. ДУ и численные методы 2 семестр

Лекция 8
Системы дифференциальных
уравнений

2.

Введение
• Во многих задачах математики, физики и техники
требуется определить несколько функций,
связанных между собой несколькими
дифференциальными уравнениями.
• Для этого необходимо располагать, вообще говоря,
таким же числом уравнений. Если каждое из этих
уравнений является дифференциальным, то есть
имеет вид соотношения, связывающего неизвестные
функции и их производные, то говорят о системе
дифференциальных уравнений.
2

3.

Основные понятия теории СДУ
Определение. Система уравнений вида
Fi t , x1 t , x1 t ,
i 1, s
, x1
m1
t ,
, xk t , xk t ,
, xk
mk
t 0,
t a, b
связывающих независимую переменную t,
неизвестные функции x1 t , , xk t и их
производные до порядков m1,m2,… mk соответственно,
называется системой обыкновенных
дифференциальных уравнений в общей форме.
Сумма порядков старших производных
неизвестных функций, входящих в СДУ, называется
порядком СДУ.
3

4.

Определение. Совокупность непрерывно
дифференцируемых на (а,b)
1 t , 2 t , , k t t , t a, b ,
функций
называется решением СДУ, если она обращает на
интервале (а,b) каждое уравнение этой системы в
тождество.
4

5.

Способы представления СДУ
1. Канонический вид.
Определение. Система, которая может быть разрешена
относительно старших производных неизвестных функций,
называется канонической:
mj
xj
t f j t; x1 t ,
m1 1
, x1
,
, xk t ,
mk 1
, xk
.
5

6.

2. Нормальный вид.
Определение.
Система уравнений
первого
порядка,
разрешенных относительно производных первого порядка
всех искомых функций, называется нормальной:
xi t fi t , x1 t ,
Замечание:
Для неизвестных функций
y1(x), y2(x),…, yn(x) СДУ
примет вид:
, xn t .
dy1
dx f 1 x, y1 , y 2 , , y n
dy 2 f x, y , y , , y
2
1
2
n
dx
dy n f x, y , y , , y
n
1
2
n
dx
6

7.

Если СДУ задана в канонической форме, то ее можно
записать в нормальной форме, обозначив производные
искомых функций через дополнительные неизвестные
функции.
Пример: записать СДУ в нормальной форме.
y x y 2
x y x
y z
Обозначим y z , тогда x z x
.
z z x y 2
7

8.

Определение.
Интегралом
дифференциальных
уравнений
нормальной
системы
называется
функция
(t , x1 , x2 ,..., xn ), определенная и непрерывная вместе с
частными производными t , x ,..., x в некоторой области D
1
n
изменения переменных и принимающая при любых x a, b
постоянное значение при подстановке в нее произвольного
решения системы.
Равенство (t , x1 , x2 ,..., xn ) C , где (t , x1 , x2 ,..., xn ) – интеграл
нормальной системы,
C
– произвольная постоянная, называется
первым интегралом системы.
8

9.

Геометрическая интерпретация СДУ в нормальной
форме
Рассмотрим для определенности нормальную систему:
dy
dx f1 ( x, y, z ),
dz f ( x, y, z ).
2
dx
Общее решение этой системы имеет вид: y y ( x, C1 , C2 ),
z z ( x, C1 , C2 ).
Каждая из функций - уравнение цилиндрической
поверхности в трехмерном пространстве,
их совокупность – кривую в Oxyz, которая является
интегральной кривой исходной системы.
9

10.

СДУ определяет в каждой точке x, y, z некоторой области
dy
пространства значения dx
dz
и dx , задающие направление,
которого касается интегральная кривая.
Нормальная система дифференциальных уравнений задает
поле направлений в пространстве.
Нахождение общего решения этой системы геометрически
означает
нахождение
двухпараметрического
семейства
кривых, в каждой своей точке касающихся направления,
задаваемого полем.
10

11.

Механическая интерпретация СДУ в нормальной
форме
Определение. Пространство переменных x1, x2 ,
, xn систе-
мы дифференциальных уравнений в нормальной форме называется фазовым пространством системы.
Уравнения системы задают значения скоростей изменения координат изображающей точки M t x1 t ,
, xn t ,
a t b.
Решение СДУ эквивалентно восстановлению координат
движущейся в пространстве R точки по известным скоростям
их изменения.
11

12.

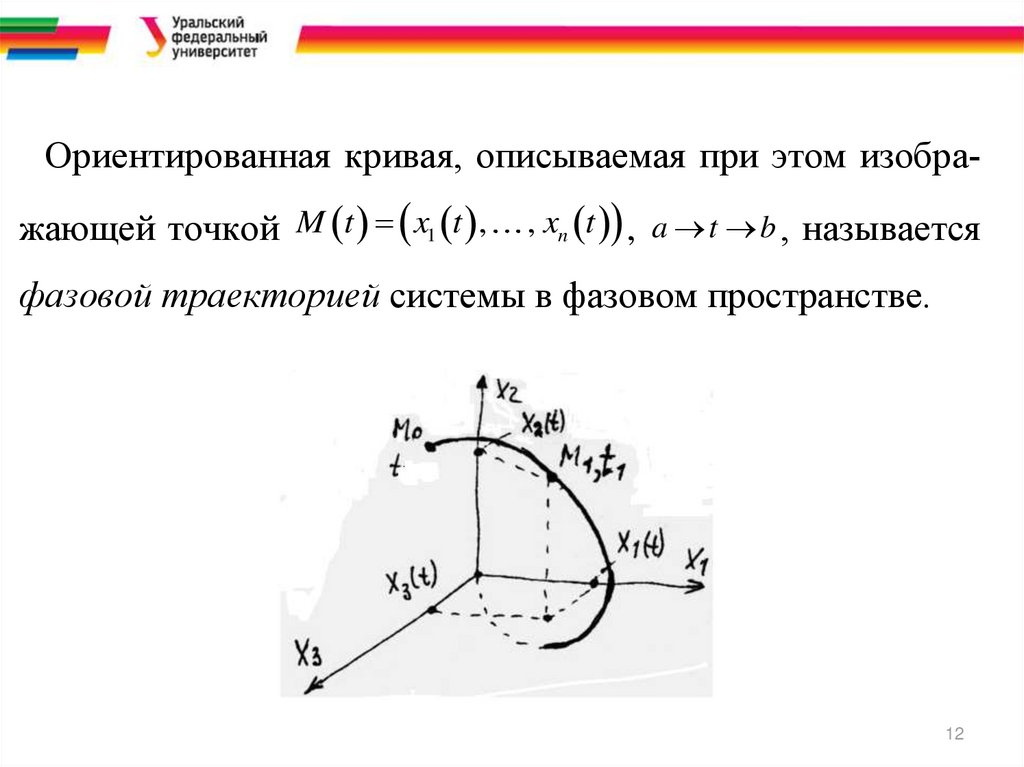
Ориентированная кривая, описываемая при этом изображающей точкой M t x1 t ,
, xn t , a t b , называется
фазовой траекторией системы в фазовом пространстве.
12

13.

Задача Коши для системы дифференциальных уравнений
состоит в том, чтобы найти такое решение, которое при x=x0
принимало бы заданные значения:
y1 x0 y10 , y 2 x0 y 20 , , y n x 0 y n0 .
Записывается задача Коши для нормальной системы
дифференциальных уравнений следующим образом
dy1
dx f1 x, y1 , y2 , , yn
dyn f n x, y1 , y2 , , yn
dx
y x y , y x y , , y x y
10
2
0
20
n
0
n0
1 0
13

14.

Теорема существования и единственности решения задачи
Коши.
Теорема. Пусть правые части уравнений системы в НФ,
т.е. функции f i x, y1 , y 2 , , y n , (i=1,2,…,n) непрерывны
по всем переменным в некоторой области D и имеет в
ней
непрерывные
частные
производные
f i f i
f i
,
, ,
y1 y 2
y n
Тогда
.
каковы
бы
ни
были
значения
x x 0 y1 y10 , y 2 y 20 , , y n y n0 ,
принадлежащие
области D, существует единственное решение
y1 x , y 2 x , , y n x ,
системы
удовлетворяющее
начальным условиям
y1 x 0 y10 , y 2 x 0 y 20 , , y n x 0 y n0 .
14

15.

Некоторые приемы аналитического решения СДУ
Сведение к одному уравнению (исключения
неизвестных)
dy1
или в векторном виде
f 1 x, y1 , y 2 , , y n
dx
dy 2 f x, y , y , , y
2
1
2
n
dx
dy n f x, y , y , , y
n
1
2
n
dx
yi (t ) fi ( x, y1 ,..., yn ), i 1,..., n
Дифференцируем по х первое уравнение системы
d 2 y1
dx 2
df 1 df 1 dy1
df 1 dy n
dx dy1 dx
dy n dx
15

16.

dy n
dy1 dy 2
Заменяя производные dx , dx , , dx
их выражениями
f 1 , f 2 , , f n из исходной системы уравнений, будем иметь
d 2 y1
F2 x, y1 , y 2 , , y n
2
dx
Дифференцируем полученное уравнение и поступая
аналогично предыдущему, найдём
d 3 y1
dx
3
F3 x, y1 , y 2 , , y n
Продолжая далее таким же образом, получим уравнение
d n y1
dx
n
Fn x, y1 , y 2 , , y n
16

17.

dy1
dx F1 x, y1 , y 2 , , y n
2
d y1
2 F2 x, y1 , y 2 , , y n
dx
..................................................
Итак, получили систему d n y
1
dx n Fn x, y1 , y 2 , , y n
Из первых п-1 уравнений определим y2 , y3 , … , yn , выразив
их через x, y и
dy1 d 2 y1
d n 1 y1
,
, ,
2
dx dx
dx n 1
.
Подставляя эти выражения в последнее из уравнений
системы, получим уравнения п-го порядка для определения y1
d n y1
n 1
x
,
y
,
y
,
,
y
1
1
1
n
dx
17

18.

Решив это уравнение, найдём y1
y1 1 x, C1 , C 2 , , C n
Дифференцируя последнее выражение п-1 раз, найдём
dy1 d 2 y1
d n 1 y1
,
, ,
2
производные
как функции от
dx dx
dx n 1
x, C1 , C 2 , , C n .
Подставляя эти функции в равенства, определяющие y2 , y3 , …
, yn , получим:
y 2 2 x , С1 , С 2 , , С n
...........................................
y x, C , C , , C .
n
1
2
n
n
Таким образом, найдено решение системы:
y1 1 x, C1 , C 2 , , C n
y x, С , С , , С
2
2
1
2
n
...........................................
y n n x, C1 , C 2 , , C n
18

19.

Пример. Найти общее решение системы уравнений:
x 5x 2 y
y 2x 2 y
Продифференцируем первое уравнение: x 5 x 2 y ;
Подставим в это выражение производную у =2x + 2y
из второго уравнения.
x 5 x 4 x 4 y;
Подставим сюда у, выраженное из первого уравнения:
Получим ОЛДУ: x 5x 4x 2x 10x
x 7 x 6x 0
x C1 e t C 2 e 6t ;
x C1 e t 6C 2 e 6t ;
x C1et C2 e6t
1
t
6t
y
2
C
e
C
e
1
2
2
2 y x 5 x C1 e t 6C 2 e 6t 5C1 e t 5C 2 e 6t ;
1
y 2C1 e C 2 e 6 t ;
2
t
19

20.

Домашнее задание
Решить СДУ сведением к одному ДУ
20

21.

Метод интегрируемых комбинаций
Законспектируйте материал из прикрепленной лекции
11 и по аналогии с примером выполните задание:
Записать СДУ в симметричной форме.
Решить методом сведения к одному ДУ
и методом интегрируемых комбинаций
21