Пирамида

1.

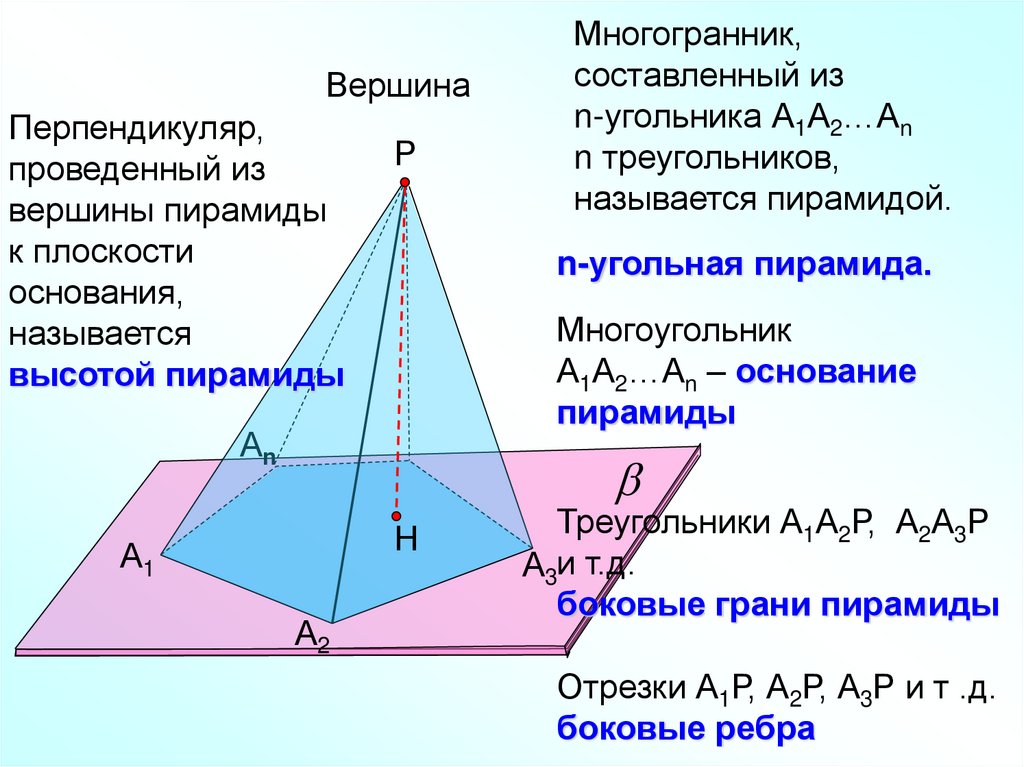
Вершина
Перпендикуляр,
проведенный из
вершины пирамиды
к плоскости
основания,
называется
высотой пирамиды
Р
Многогранник,
составленный из
n-угольника А1А2…Аn
n треугольников,
называется пирамидой.
n-угольная пирамида.
Многоугольник
А1А2…Аn – основание
пирамиды
Аn
Н
А1
А2
Треугольники А1А2Р, А2А3Р
А3и т.д.
боковые грани пирамиды
Отрезки А1Р, А2Р, А3Р и т .д.
боковые ребра

2.

SS
Н
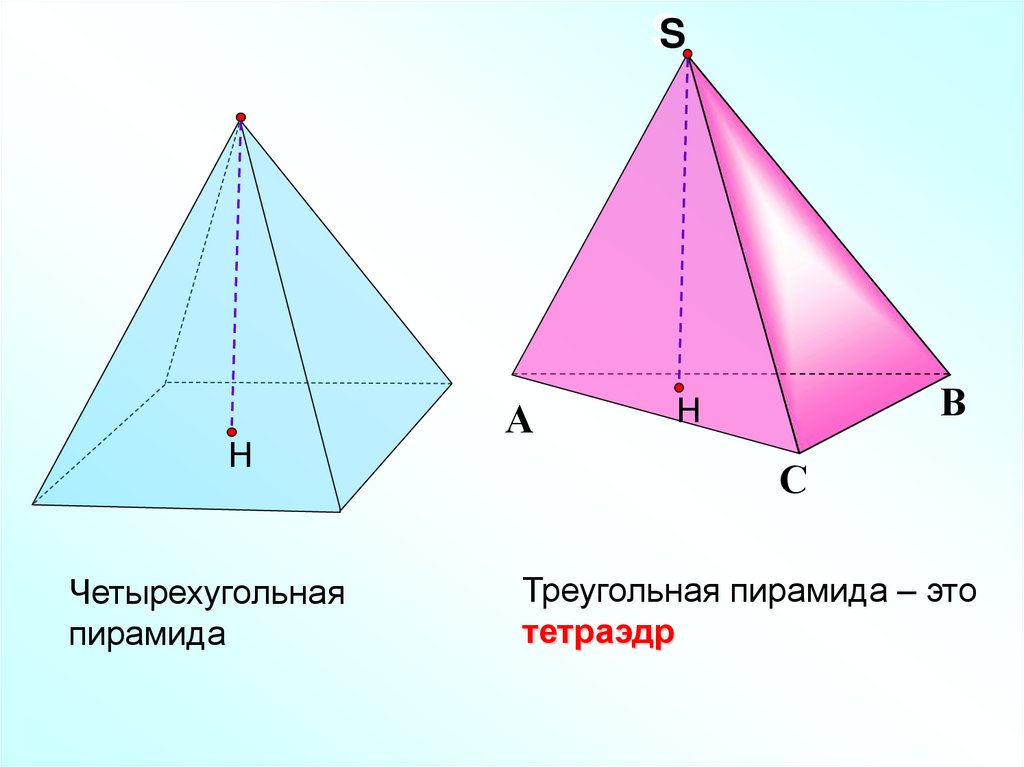
Четырехугольная
пирамида
А
В
Н
С
Треугольная пирамида – это
тетраэдр

3.

Пятиугольная
пирамида
Р
Шестиугольная
пирамида
Аn
Н
А1
А3
А2
Н
Sполн Sбок Sосн

4.

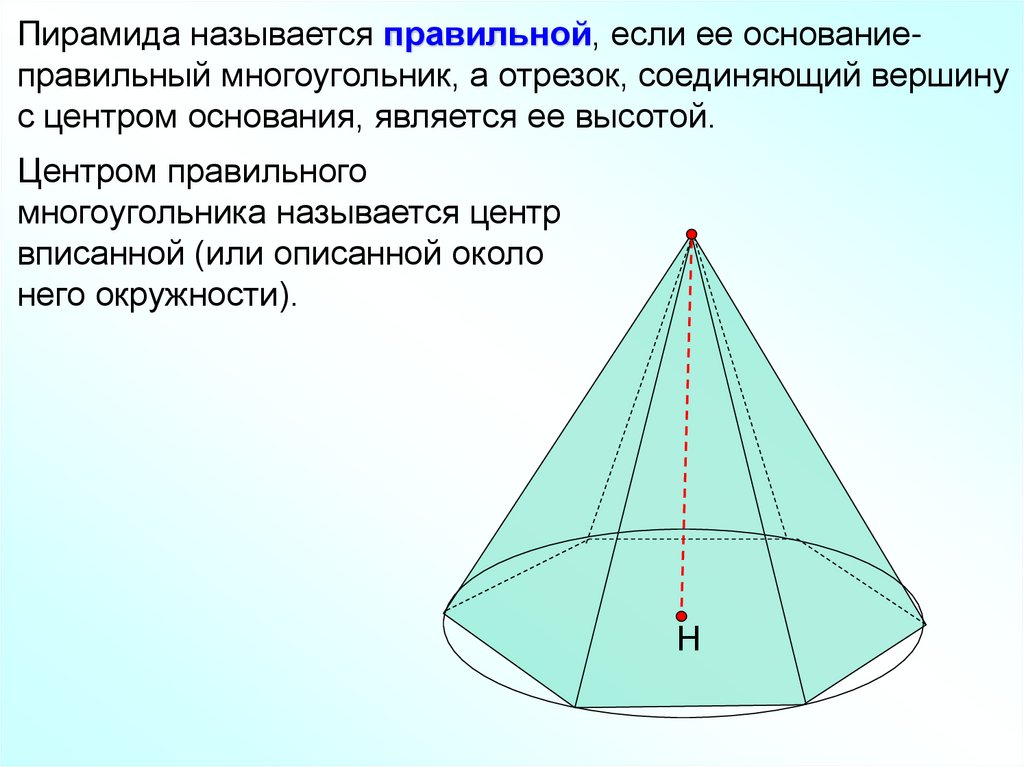
Пирамида называется правильной, если ее основаниеправильный многоугольник, а отрезок, соединяющий вершину
с центром основания, является ее высотой.
Центром правильного
многоугольника называется центр
вписанной (или описанной около
него окружности).
Н

5.

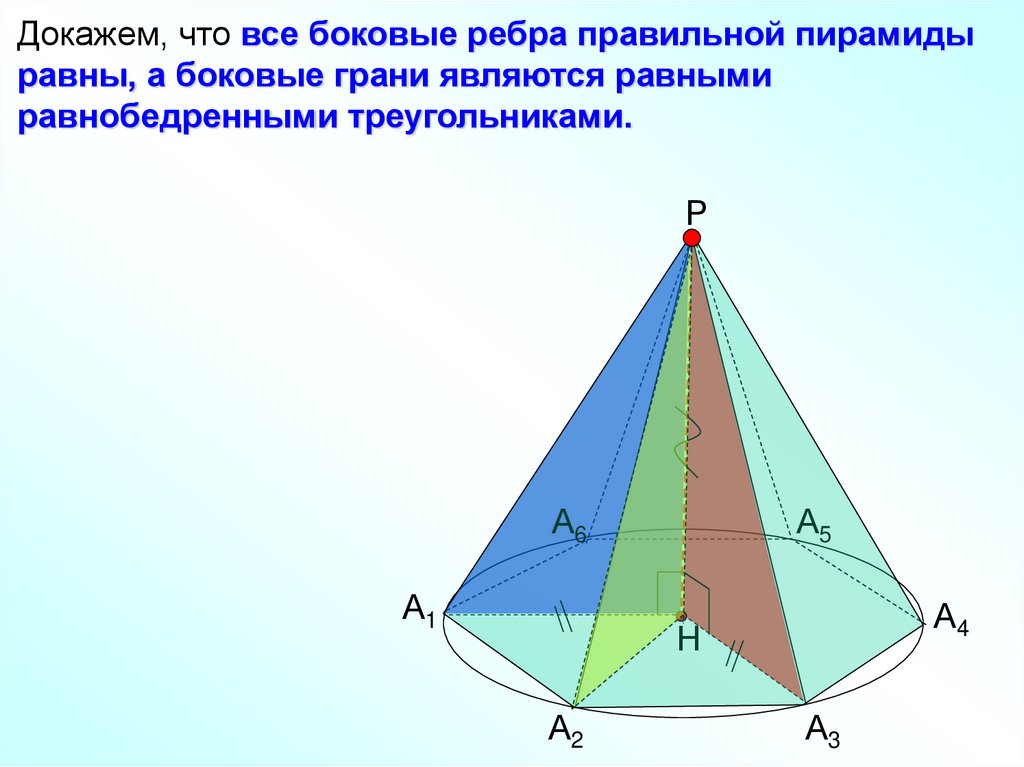
Докажем, что все боковые ребра правильной пирамиды
равны, а боковые грани являются равными
равнобедренными треугольниками.
Р
А6
А1
А5
А4
Н
А2
А3

6.

Высота боковой грани правильной пирамиды, проведенная из
ее вершины, называется апофемой.
Р
А6
А1
А5
А4
Н
А2
А3

7.

Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на
апофему.
S бок
1
Росн h
2
Р
h
А6
А1
А5
А4
Н
А2
А3

8.

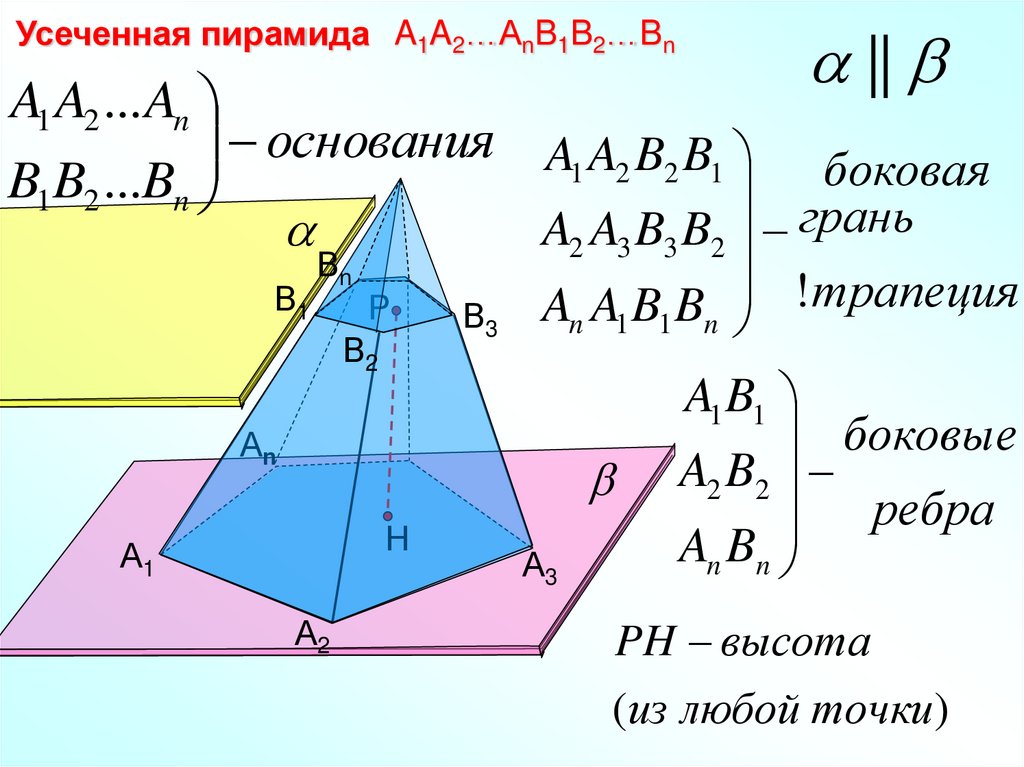
Усеченная пирамида A1A2…AnB1B2…Bn
||
A1 A2 ... An
основания A A B B
1 2 2 1
боковая
B1B2 ...Bn
A2 A3 B3 B2 грань
В1
Вn
Р
В2
В3
An A1 B1 Bn ! трапеция
Аn
Н
А1
А2
А3
A1 B1
боковые
A2 B2
ребра
An Bn
PH высота
(из любой точки )

9.

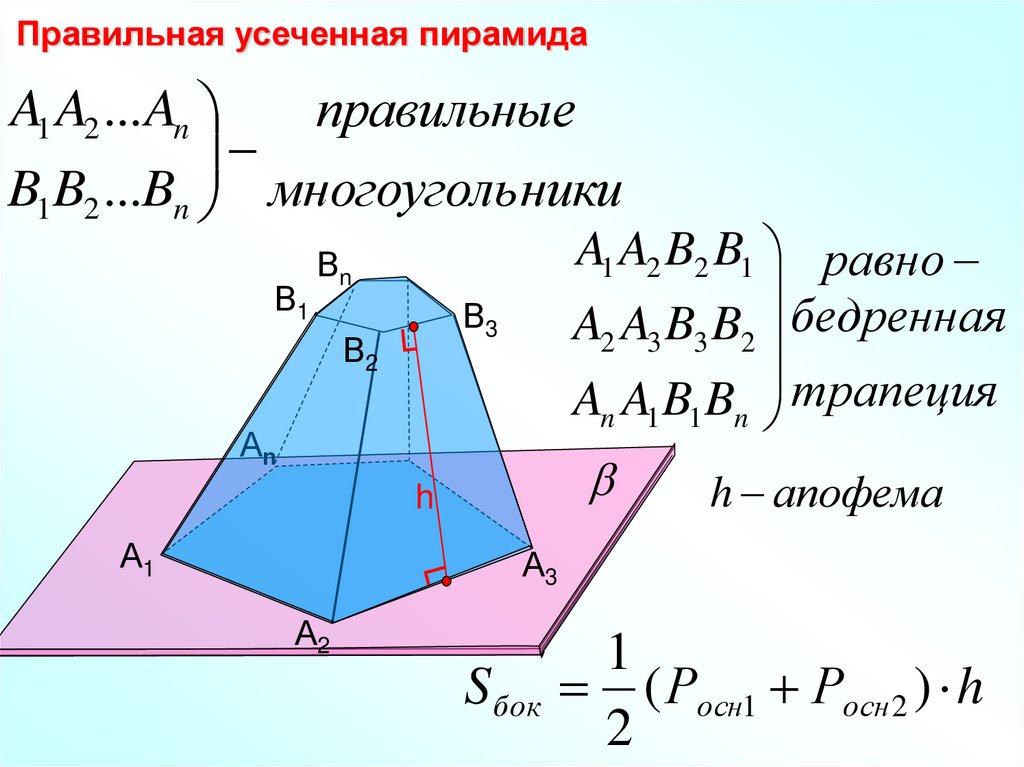
Правильная усеченная пирамида
A1 A2 ... An
правильные
B1B2 ...Bn многоугольники
В1
A1 A2 B2 B1 равно
A2 A3 B3 B2 бедренная
An A1 B1 Bn трапеция
Вn
В3
В2
Аn
h
А1
h апофема
А3
А2
S бок
1
( Росн1 Росн 2 ) h
2