Similar presentations:
Пирамида. 10 класс
1.
2.
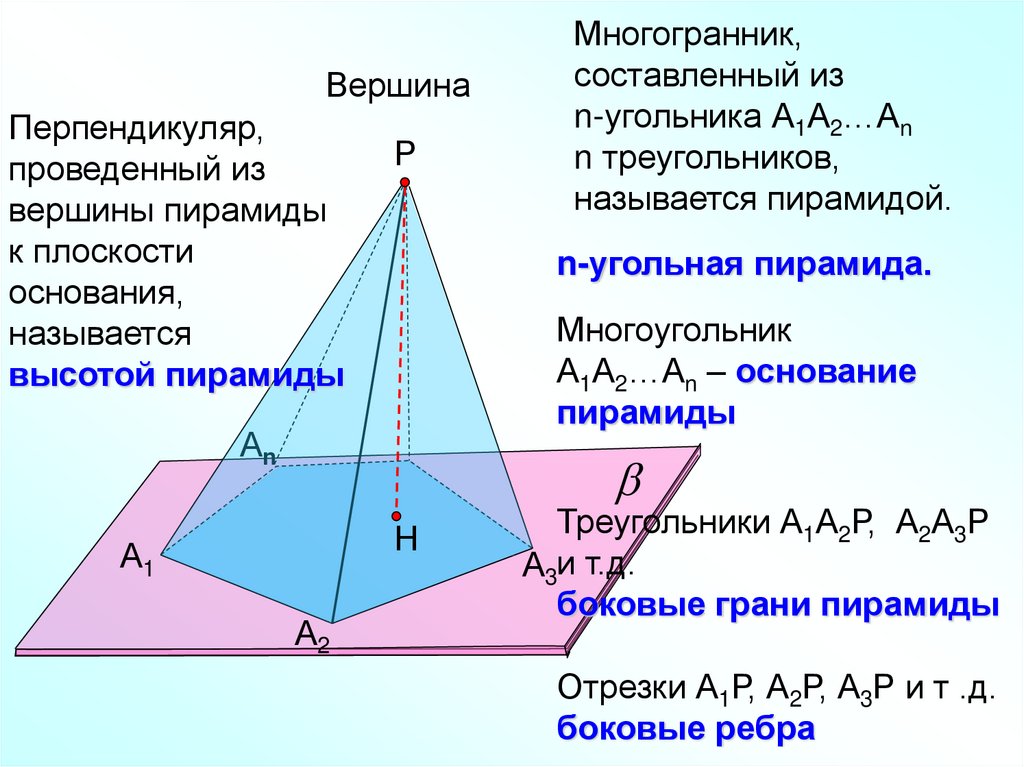
ВершинаПерпендикуляр,
проведенный из
вершины пирамиды
к плоскости
основания,
называется
высотой пирамиды
Р
Многогранник,
составленный из
n-угольника А1А2…Аn
n треугольников,
называется пирамидой.
n-угольная пирамида.
Многоугольник
А1А2…Аn – основание
пирамиды
Аn
Н
А1
А2
Треугольники А1А2Р, А2А3Р
А3и т.д.
боковые грани пирамиды
Отрезки А1Р, А2Р, А3Р и т .д.
боковые ребра
3.
SSН
Четырехугольная
пирамида
А
В
Н
С
Треугольная пирамида – это
тетраэдр
4.
Пятиугольнаяпирамида
Р
Шестиугольная
пирамида
Аn
Н
А1
А3
А2
Н
Sполн Sбок Sосн
5.
№ 239. Основанием пирамиды является ромб, сторонакоторого равна 5 см, а одна из диагоналей 8 см. Найдите
боковые ребра пирамиды, если ее высота проходит через
точку пересечения диагоналей основания и равна 7 см.
Н
7
D
4
А
5 см
8
O
С
5 см
3
В
6.
№ 243. Основанием пирамиды DАВС является треугольникАВС, у которого АВ = АС = 13 см, ВС = 10 см; ребро АD
перпендикулярно к плоскости основания и равно 9 см.
Найдите площадь боковой поверхности пирамиды.
D
9
13
В
10
M
А
13
С
7.
Пирамида называется правильной, если ее основаниеправильный многоугольник, а отрезок, соединяющий вершинус центром основания, является ее высотой.
Центром правильного
многоугольника называется центр
вписанной и описанной около него
окружности.
Н
8.
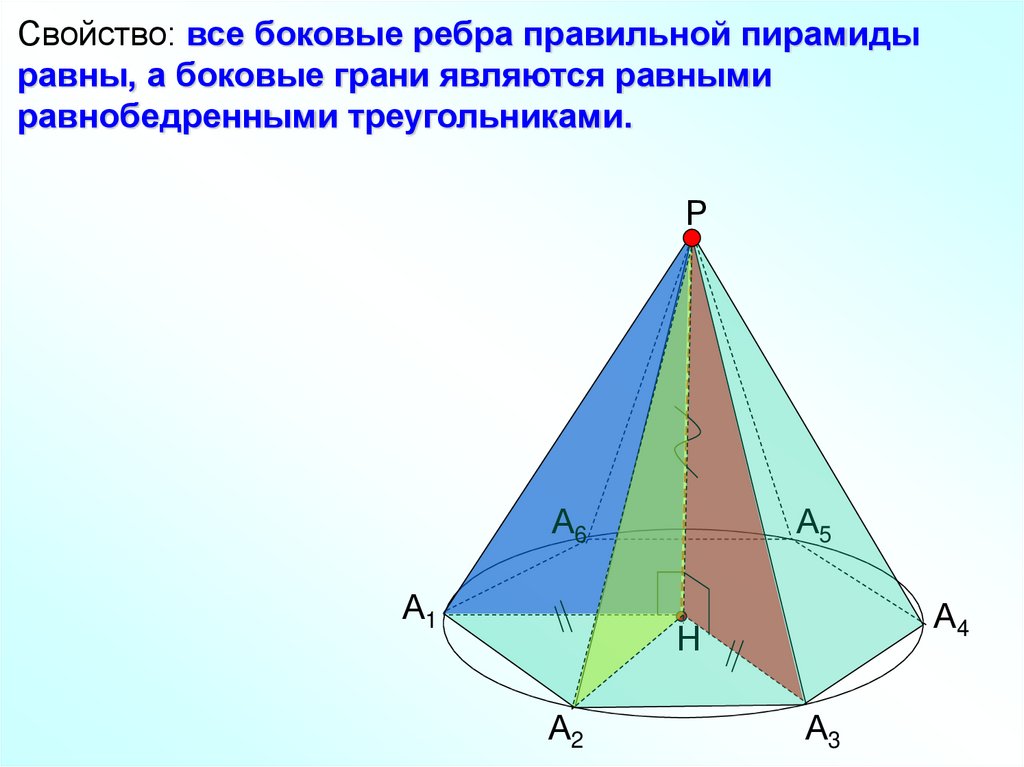
Свойство: все боковые ребра правильной пирамидыравны, а боковые грани являются равными
равнобедренными треугольниками.
Р
А6
А1
А5
А4
Н
А2
А3
9.
Высота боковой грани правильной пирамиды, проведенная изее вершины, называется апофемой.
Р
А6
А1
А5
А4
Н
А2
А3
10.
Площадь боковой поверхности правильной пирамидыравна половине произведения периметра основания на
апофему.
S бок
1
Росн h
2
Р
h
А6
А1
А5
А4
Н
А2
А3
11.
№240. Основанием пирамиды является параллелограмм,стороны которого равны 20 см и 36 см, а площадь равна
360 см2. Высота пирамиды проходит через точку пересечения
диагоналей основания и равна 12 см. Найти S полн.поверх.
Н
D
12
О
O
А
М
36
С
С
D
K
B
20
А
K
В
12.
№ 244. Основанием пирамиды DАВС являетсяпрямоугольный треугольник АВС, у которого гипотенуза АВ =
29 см, катет АС = 21 см. Ребро АD перпендикулярно к
плоскости основания и равно 20 см. Найдите Sбок.
D
20
29
В
А
21
С










 mathematics
mathematics








