Резонансные явления в электрических цепях

1.

1
РЕЗОНАНСНЫЕ ЯВЛЕНИЯ В
ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

2.

Резонансные явления могут возникать в
электрических цепях, содержащих индуктивности и
емкости.
Резонанс в цепи с последовательным соединением
индуктивности и емкости называют резонансом
напряжений или последовательным резонансом.
При параллельном соединении тех же элементов
может возникать резонанс токов.
В сложной разветвленной цепи могут иметь место
оба вида резонанса.
2

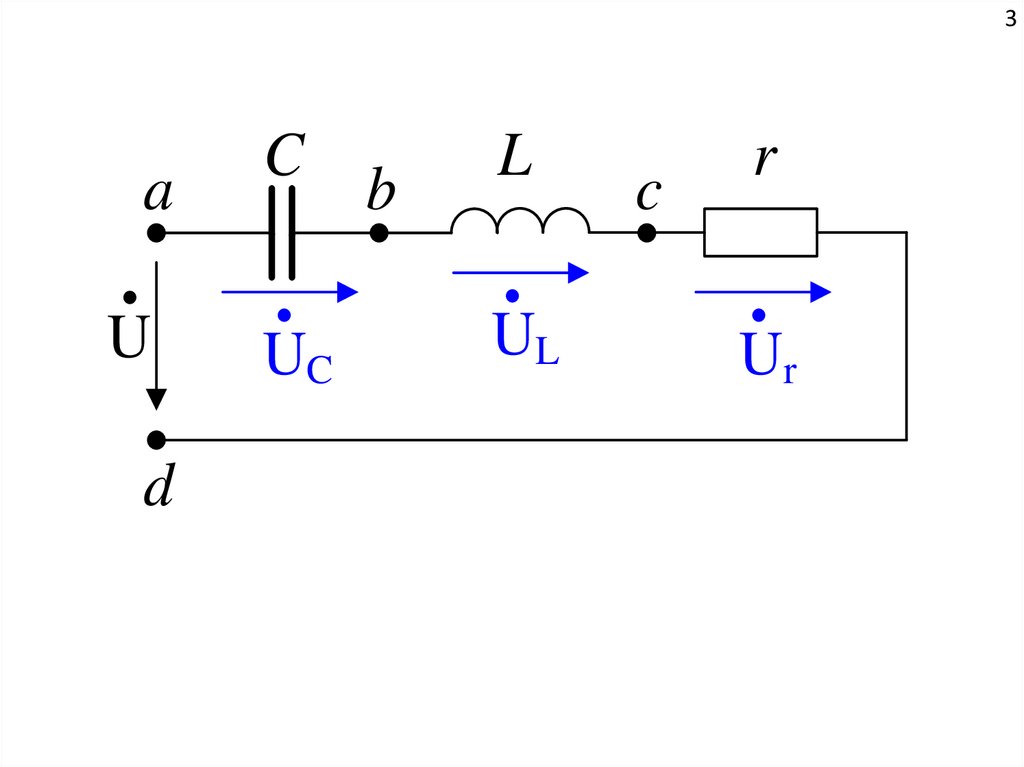
3.

3
a
U
d
C
UC
b
L
UL
c
r
Ur

4.

4
Входное комплексное сопротивление этой схемы:
2
1
1 j
2
Z r j L
r L
e
C
C
где
1
L
C
arctg
.
r
(3.44)

5.

Изменяя частоту, индуктивность или емкость, можно
добиться равенства нулю реактивного сопротивления в
составе (3.44).
Изменяя частоту при неизменных значениях
индуктивности и емкости, придем к условию
1
0 L
0
0C
,
которое рассматривается как условие резонанса.
5

6.

6
Угловая частота
1
0
LC
называется резонансной.
При резонансе напряжений, как следует из выражения
(3.44), входное сопротивление становится чисто
активным:
Z = r.
Это значение является минимальным, поэтому ток I0 в
схеме становится максимальным.

7.

7
Из (3.44) также следует, что угол φ = 0 и входной ток
цепи совпадает по фазе с напряжением.
Совпадение по фазе входного напряжения и тока
является основным признаком наличия резонанса не
только в рассматриваемом контуре, но и в любой другой
цепи.

8.

Напряжения UL и UC при последовательном
соединении элементов L и С находятся в
противофазе.
Если xL ≠ xC, их амплитуды и действующие
значения неодинаковы.
При выполнении условия резонанса,
xL = xC , амплитуды становятся одинаковыми.
Отсюда и название «резонанс напряжений».
8

9.

9
Характеристическое или волновое
сопротивление контура:
L
C

10.

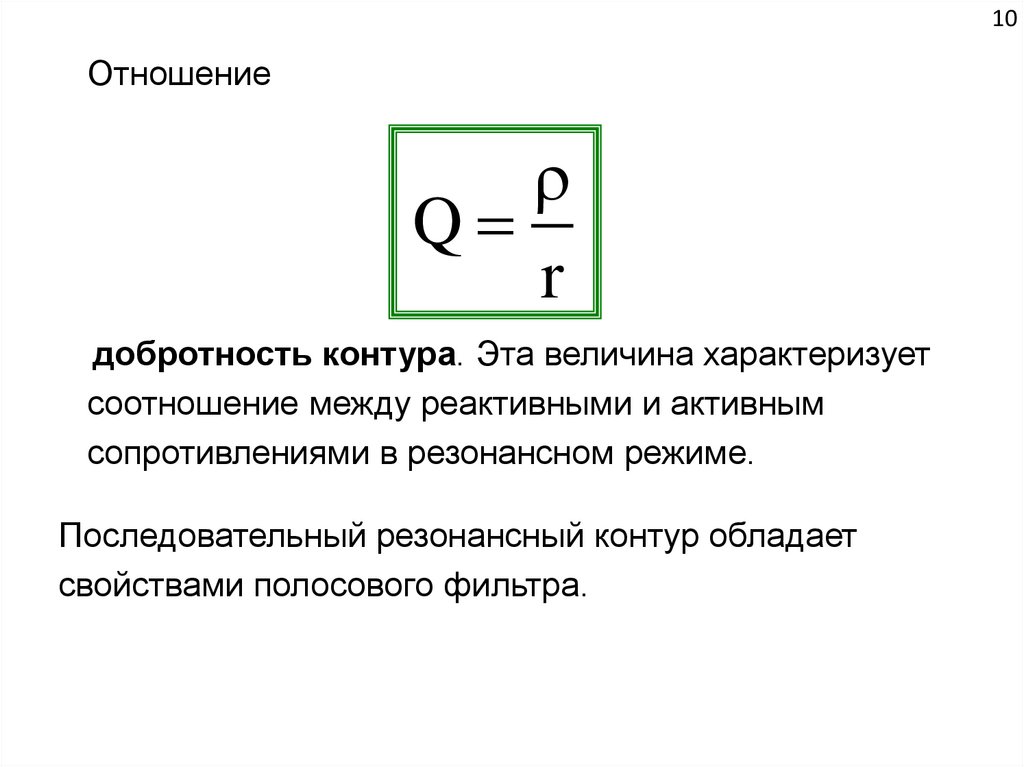
10
Отношение
Q
r
добротность контура. Эта величина характеризует
соотношение между реактивными и активным
сопротивлениями в резонансном режиме.
Последовательный резонансный контур обладает
свойствами полосового фильтра.

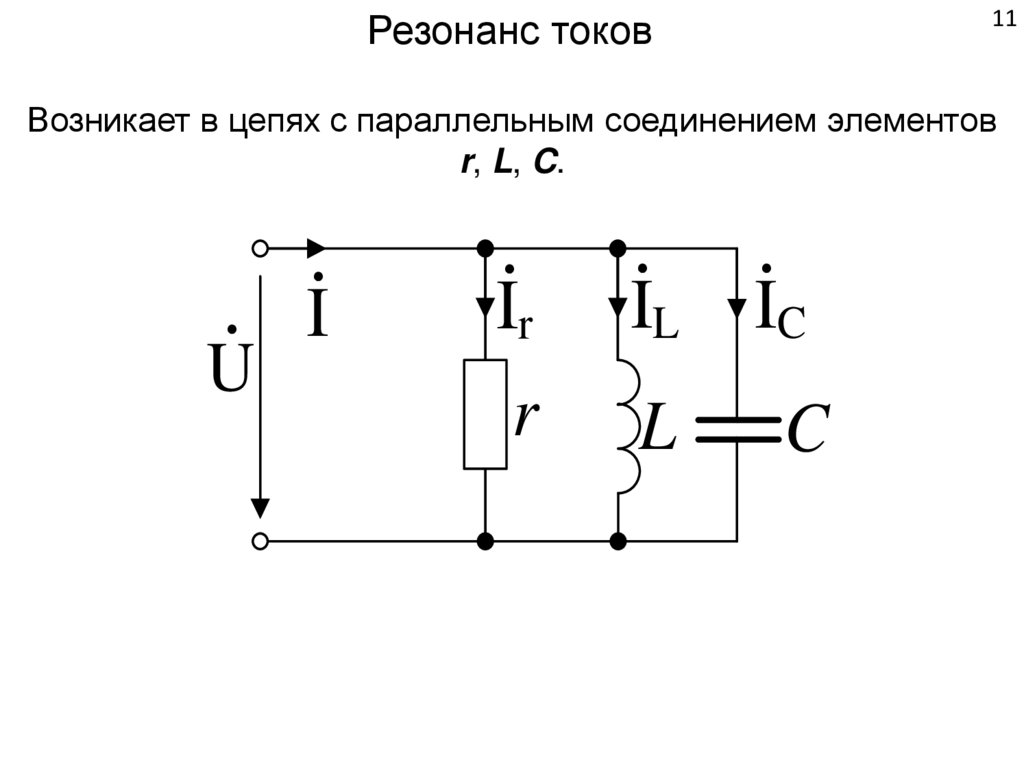
11.

11
Резонанс токов
Возникает в цепях с параллельным соединением элементов
r, L, C.
·U
·I
·Ir
·IL ·IC
r
L
C

12.

12
·
U
r
L
C
Входная комплексная
проводимость схемы:
1
j
Y g j(b L bC ) g j
C ye
L
2
где
b L bC
1
y g
C ; arctg
g
L
2

13.

13
При резонансной частоте реактивная проводимость
принимает нулевое значение:
1
0C 0.
0 L
Откуда резонансная частота
1
0
.
LC

14.

14
Проводимость g=1/r есть минимальное значение входной
проводимости (максимальное значение входного
сопротивления).
Поэтому при резонансе токов входной ток схемы
принимает минимальное значение:
I0 I r0 gU.

15.

15
Схема с параллельным соединением
элементов r, L, C обладает характеристиками
заграждающего или режекторного фильтра.
В области частот, примыкающей к резонансной,
входное сопротивление цепи максимально.
Поэтому ток минимален, откуда и название
«заграждающий фильтр».