Теория электрических цепей

1. Дисциплина: Теория электрических цепей

2. Лекция №7

Тема: Резонансные
явления в
колебательных
контурах. Частотные
характеристики

3. Учебные вопросы

1. Резонанс в последовательном
колебательном контуре.
2. Частотные характеристики
последовательного колебательного контура.
3. Избирательные свойства
последовательного колебательного контура.
4. Резонанс в параллельном колебательном
контуре.
5. Частотные характеристики параллельного
колебательного контура.

4. Литература

Попов В.П. Основы теории
цепей: Учебник для вузов
спец. "Радиотехника".-М.:
Высшая школа, 2007. с.
199-218, с.218-260.

5. Режимы работы последовательной RLC-цепи

Векторные диаграммы напряжений и токов
Активно-индуктивный
Активно-ёмкостной
Активный
(резонанс напряжений)

6. Свойства активно-индуктивного режима последовательной RLC-цепи

Свойства активноиндуктивного режима
последовательной RLC-цепи
xL xC
U L xL I U C xC I
1
L
c
0
- напряжение опережает ток
источника;
- цепь имеет индуктивный
характер;

7. Свойства активно-ёмкостного режима последовательной RLC-цепи

xL xC
U L xL I U C xC I
1
L
c
0
- напряжение отстает от тока
источника;
- цепь имеет емкостной
характер;

8. Свойства режима резонанса напряжений последовательной RLC-цепи

xL xC
U L xL I U C xC I
1
L
c
0
- напряжение на индуктивном и емкостном
элементах полностью компенсируют друг друга,
т.к. , а напряжение на резистивном элементе
становится равным напряжению источника и
совпадает по фазе с током;
- сопротивление цепи имеет чисто резистивный
характер;

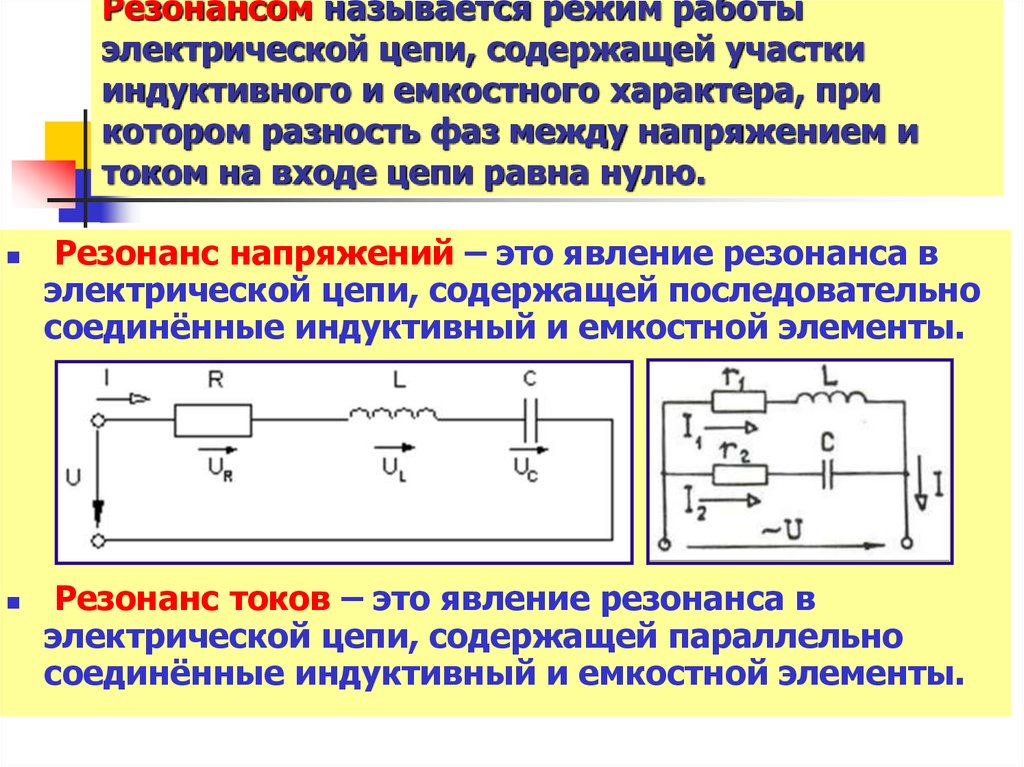
9. Резонансом называется режим работы электрической цепи, содержащей участки индуктивного и емкостного характера, при котором

разность фаз между напряжением и
током на входе цепи равнa нулю.
Резонанс напряжений – это явление резонанса в
электрической цепи, содержащей последовательно
соединённые индуктивный и емкостной элементы.
Резонанс токов – это явление резонанса в
электрической цепи, содержащей параллельно
соединённые индуктивный и емкостной элементы.

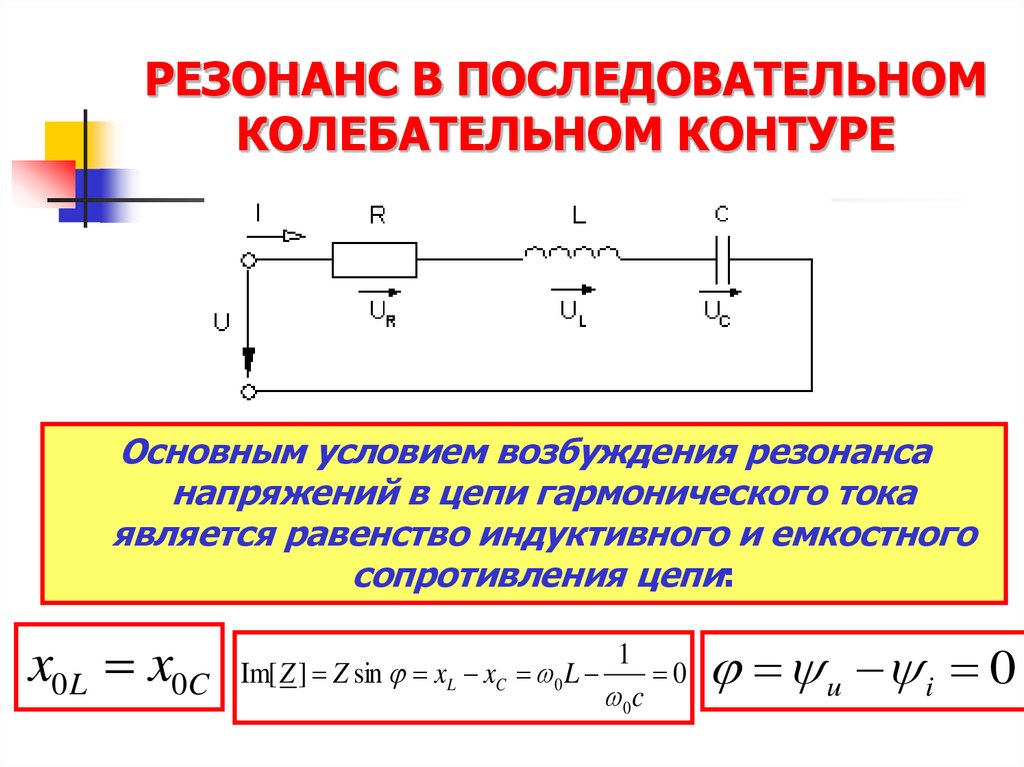
10. РЕЗОНАНС В ПОСЛЕДОВАТЕЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Основным условием возбуждения резонанса
напряжений в цепи гармонического тока
является равенство индуктивного и емкостного
сопротивления цепи:
x0 L x0C
Im[ Z ] Z sin xL xC 0 L
1
0
0 c
u i 0

11. Характеристики резонанса напряжений

1. Резонансная частота:
0 L
1
0С
0
2. Характеристическое
1
LC
(волновое) сопротивление:
0 L
1
0 c
L
C
3. Добротность и затухание контура
Q
R
1
R
d
Q

12. Способы возбуждения резонанса

1 способ. При неизменных параметрах цепи
(L = const, C = const) необходимо изменять
угловую частоту напряжения источника
питания (ω = var), приближая ее к собственной
частоте цепи:
0
2 способ. При неизменной угловой частоте напряжения
источника питания ( ω= const) необходимо изменять
собственную угловую частоту цепи, изменяя ее
параметры (L = var, C = var) и обеспечивая
приближение собственной частоты контура к частоте
напряжения источника питания:
0

13.

Свойства цепи при
резонансе напряжений
1. Полное сопротивление цепи в резонансном
режиме имеет чисто резистивный характер,
равно сопротивлению резистивного элемента и
является минимальным:
Z R j ( x L xC )
Z Z R 2 ( xL xC ) 2
x0 L x0C
x 0 x 0L x 0C 0
Z0
R02 x02 R0 Z min

14.

Свойства цепи при
резонансе напряжений
2. Ток в цепи при резонансе напряжений
является максимальным и по характеру
чисто активным, т.е. не имеет сдвига по
фазе по отношению к напряжению:
U
I0
Z0
U
R02 ( x0 L
U
U
I max
R0 Z min
x0C ) 2
x0 L x0C
x0
0 u i arctg
arctg
0
R0
R0

15.

Свойства цепи при
резонансе напряжений
3. Коэффициент мощности цепи равен
единице, полная мощность равна
активной. Это означает, что ток в цепи
при резонансе совершает максимальную
полезную работу.
0 0 cos 1
0
P0 S0 cos 0 UI0 cos 0 UI0 S0
S0 P02 Q02 P02 (Q0 L Q0C )2 ( I 02 R)2 [( I 02 x0 L ) ( I 02 x0C )]2 I 02 R P0

16.

Свойства цепи при
резонансе напряжений
4. В цепи имеют место обратимые преобразования энергии
электрического и магнитного полей, причем интенсивность
этих преобразований одинакова: энергия электрического
поля конденсатора и энергия магнитного поля катушки
преобразуются одна в другую с одинаковой скоростью .
Q0 L I x Q0C I x 0
2
0 0L
2
0 0C
Q0 Q0 L Q0C 0
Q0C 0, Q0 L 0
Все колебания энергии (обратимые ее преобразования)
имеют место только в пределах внешней цепи, возврата
энергии к источнику нет .

17.

Свойства цепи при
резонансе напряжений
5. Энергия, потребляемая контуром от
источника, равна энергии, теряемой в
активном сопротивлении контура R.
Колебательный процесс в контуре без
потерь должен иметь незатухающий
характер.
T
T
T
0
0
0
W П uidt 2U 0 cos( 0t ) 2I 0 cos( 0t ) dt 2RI 02 cos 2 ( 0t )dt RI 02T

18. Физический смысл добротности контура

Wзап
LI 02
L
WП
RI 02T
RT
Wзап 0 L
1
Q
WП
2 R 2 R 2
1
2
T
f0
0
Q 2
Wзап
WП
Добротность колебательного контура
характеризует свойство колебательного контура
запасать энергию в реактивных элементах, она
равна отношению энергии, запасаемой в
контуре, к энергии потребляемой контуром за
период колебаний, умноженному на 2π.

19.

Свойства цепи при
резонансе напряжений
6. Действующие значения напряжений на
реактивных элементах равны между собой:
U
U 1
U 0 L U 0C I 0 x0 L I 0 x0C 0 L
R
R 0 c
U 0 L U 0C 1 L
Q
U
U
R C R
U L
U LC U L
U U Q
R LC R C
R C
R
Добротность контура показывает во
сколько раз напряжения на
реактивных элементах контура при
резонансе превышает значение
приложенного к контуру
напряжения.

20. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПОСЛЕДОВАТЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА

Зависимости от частоты параметров контура:
x( ) xL ( ) xC ( )
Фазо-частотная
характеристика
1
L
x( )
c
( ) arctg
arctg
R
R
Амплитудно-частотные характеристики – это зависимости
действующих или амплитудных значений тока и
напряжения от частоты:
I ( )
U L ( )
U C ( )

21. Амплитудно-частотные характеристики

U
I ( )
Z ( )
U
1 2
R ( L )
c
2
U L
U L ( ) I ( ) xL ( )
1 2
R ( L )
c
2
U C ( ) I ( ) xc ( )
U
1 2
c R ( L )
c
2
U
R2
1 2
(
1
)
2 2
2
L
LC
U
R 2 2c 2 ( 2 LC 1) 2

22.

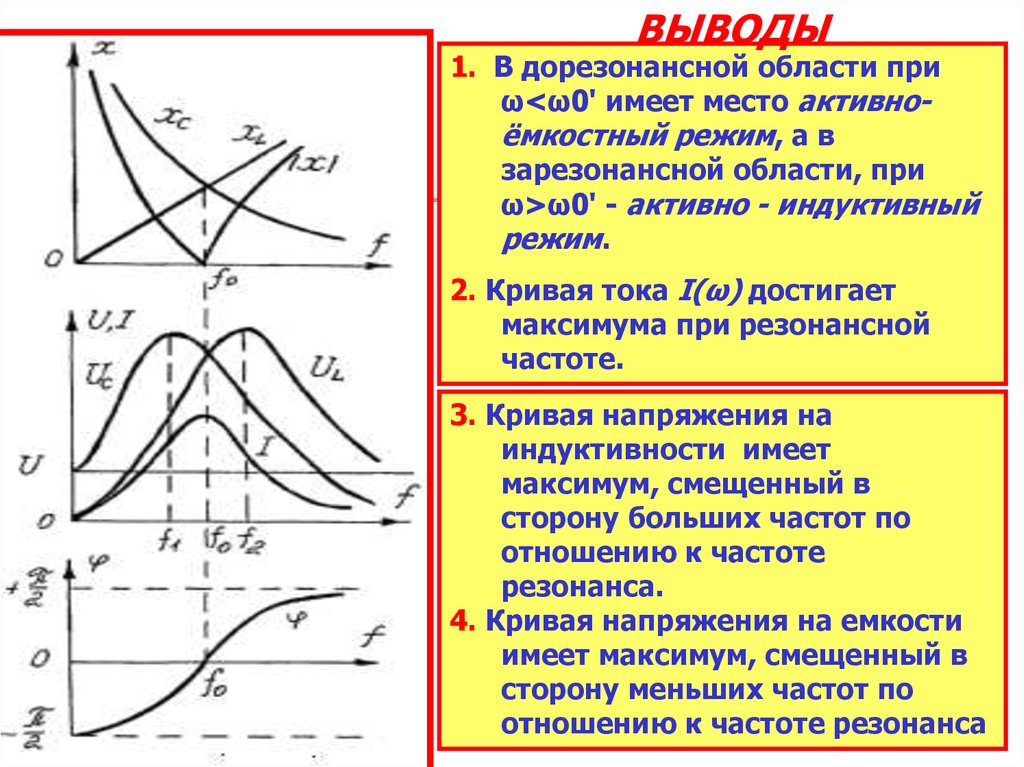
ВЫВОДЫ
1. В дорезонансной области при
ω<ω0' имеет место активноёмкостный режим, а в
зарезонансной области, при
ω>ω0' - активно - индуктивный
режим.
2. Кривая тока I(ω) достигает
максимума при резонансной
частоте.
3. Кривая напряжения на
индуктивности имеет
максимум, смещенный в
сторону больших частот по
отношению к частоте
резонанса.
4. Кривая напряжения на емкости
имеет максимум, смещенный в
сторону меньших частот по
отношению к частоте резонанса

23. Расстройки колебательных контуров

Абсолютная расстройка – разность между частотой колебаний,
подводимых к контуру от источника, и резонансной частотой
контура
0
Относительная расстройка – отношение абсолютной расстройки к
резонансной частоте.
Обобщенная расстройка –
0
0
Q( )
0
Обобщенная расстройка для случая
малых расстроек -
2Q
0

24. Нормированная амплитудно-частотная характеристика

I
U R
R
f( )
2
2
2
2
I0
0
R x U
R x ( )
xL xC 2
0 1 2
1
1 2
1 0
Z R x R 1 (
) R 1 2 ( L ) R 1 2 ( L
)
R
R
c
R 0
0 c
2
2
02 L2 0 2
R 1 2 ( )
R 0
0 L
0 2
Z R 1 Q ( ) R 1 2
0
2
Q
R
0
x
Q( )
0
R

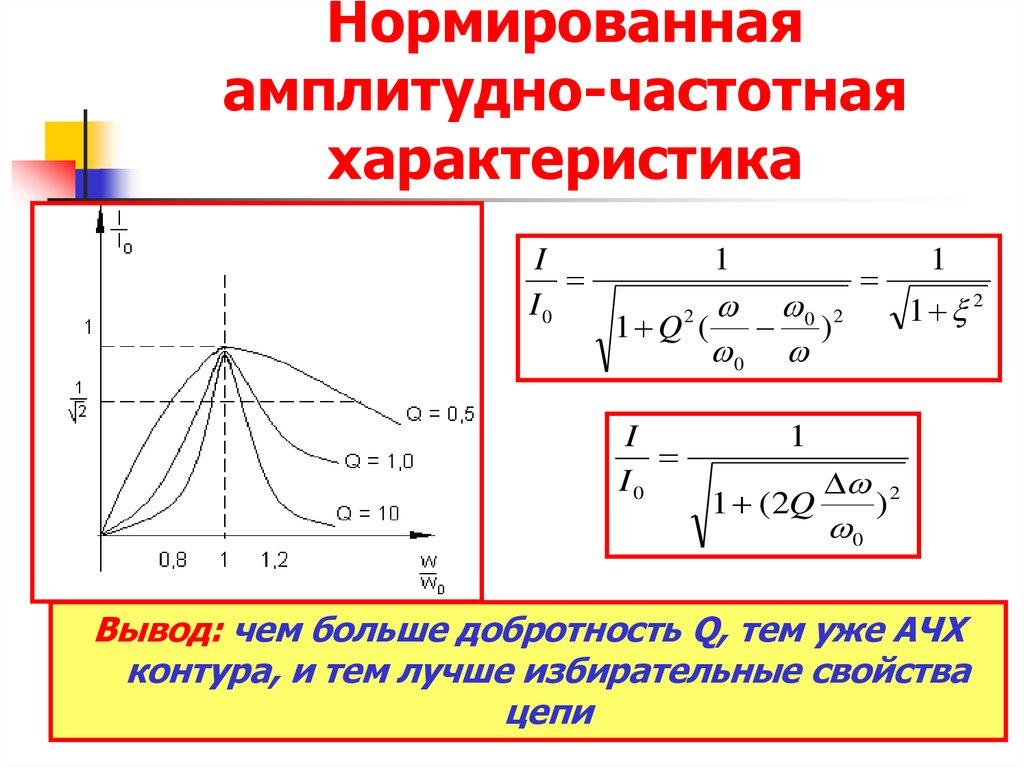
25. Нормированная амплитудно-частотная характеристика

I
I0
1
0 2
1 Q ( )
0
2
I
I0
1
1 2
1
1 ( 2Q
0
)2
Вывод: чем больше добротность Q, тем уже АЧХ
контура, и тем лучше избирательные свойства
цепи

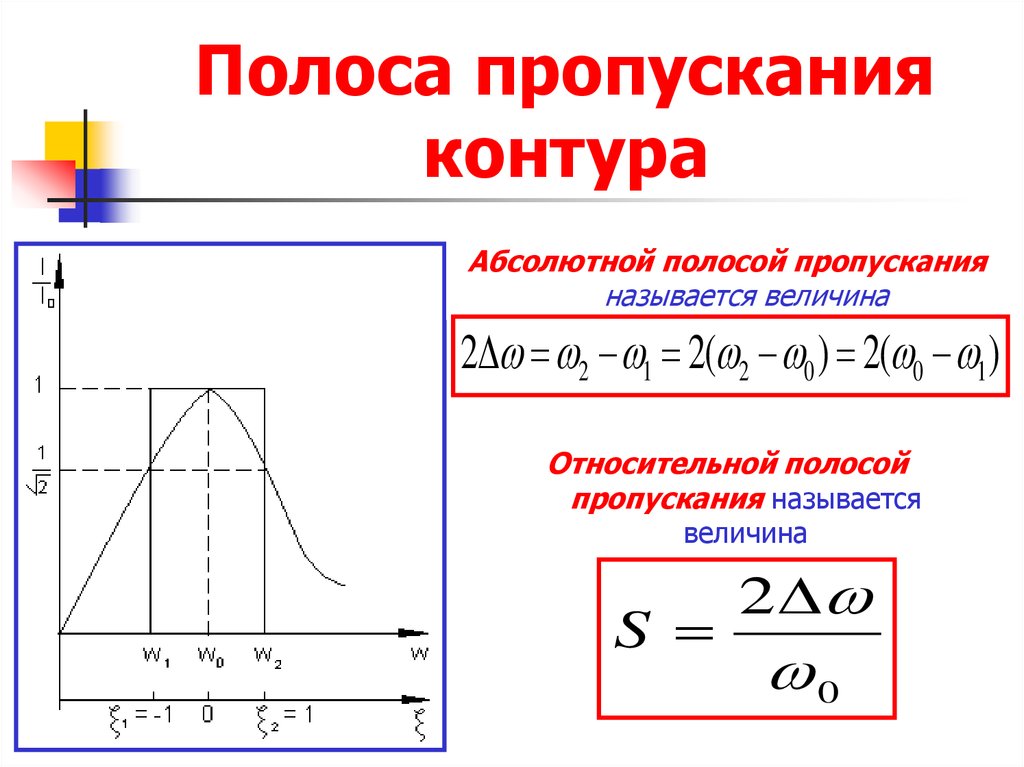
26. Полоса пропускания контура

Абсолютной полосой пропускания
называется величина
2 2 1 2( 2 0 ) 2( 0 1 )
Относительной полосой
пропускания называется
величина
S
2
0

27. Полоса пропускания контура

Граничная частота – это та частота, при которой средняя
мощность, поглощаемая последовательным контуром,
вдвое меньше средней мощности, поглощаемой при
резонансе:
P
I 2R
1
2
P0
I0 R
2
I
1
1
I0
2
1 2
0
1, 2 1 ( )Q
0
Полоса пропускания последовательного
колебательного контура – это диапазон
частот, в пределах которого значения АЧХ
составляют не менее , чем
ее
максимального значения на резонансной частоте

28. Граничные частоты

2 0
1 0
1 ( )Q 1 2 ( )Q 1
0 2
0 1
1
1
2Q
1
1 0
2
4Q
0
2 2 1
0 d
Q
1
2
2Q
S
2
0
1
1 0
2
4Q
1
d
Q
Вывод: полоса пропускания, характеризующая
избирательные свойства колебательного контура,
пропорциональна резонансной частоте и обратно
пропорциональна добротности; относительная полоса
пропускания равна затуханию контура.

29. Параллельный колебательный контур

Y1 =
1
Z1
=
R1
2
R1 ( L ) 2
1
R1 j L
=
L
-j
= g1 + jb1,
2
2
R1 ( L)
1
1
R2
1
C
Y2 =
=
=
+
= g2+ jb2
1
1 2
1
2
2
R2 j
R2 ( )
Z2
R2 (
)2
C
C
C
Параллельным колебательным контуром называется электрическая
цепь, в которой индуктивность и емкость включены параллельно
источнику сигнала.
j

30. РЕЗОНАНС В ПАРАЛЛЕЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Основным условием возбуждения
резонанса токов в цепи
гармонического тока является
равенство индуктивного и
емкостного проводимостей цепи:
b 0 L b 0C
0 ' L
2
2
R1 ( 0 ' L)
1
0 'C
R
2
2
1
(
)
0 'C

31. Резонансная частота и способы возбуждения резонанса токов

1
ω0'=
LC
L
2
R1
C
L
2
R2
C
= ω0
R1
2
2
R2
2
2
Вывод: резонанса токов можно добиться
теми же способами, которыми
обеспечивается резонанс напряжений:
изменением частоты приложенного к
цепи напряжения ω или собственной
резонансной частоты ω0', т.е. на основе
равенства ω=ω0'.

32.

Свойства цепи при
резонансе токов
1. Полная проводимость цепи при резонансе токов
имеет резистивный характер и является
минимальной.
Y0
Y=g+j (bС-bL)
y Y g 2 (bC bL ) 2
b 0 L b 0C
b0 b0L b0C 0
g b g 0 Y min
R1
2
( 0 ' L )
2
0
2
0
R1
2

33.

Свойства цепи при
резонансе токов
2. Ток в цепи при резонансе токов является
минимальным и по характеру чисто
активным, т.е. не имеет сдвига по фазе по
отношению к напряжению:
I0 = y0 ∙U = U∙
g 0 b0
2
2
= U ∙g0 = U∙ymin= =Imin
b 0C b 0 L
b0
0 u i arctg
arctg
0
g0
g0

34. Свойства цепи при резонансе токов

3. Действующие значения
токов ветвей контура на
резонансной частоте
одинаковы:
I 0 L I 0C
U
Ub0 L Ub0C I 0
R1

35. Свойства цепи при резонансе токов

4. Добротность параллельного
колебательного контура совпадает с
добротностью последовательного контура,
составленного из тех же элементов.
Q=
I0L
=
I0
I 0C
I0
=
R1
1
=
R1
L
C

36. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПАРАЛЛЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА

Зависимости от частоты параметров контура:
b ( ) bL ( ) bC ( )
Фазо-частотная
характеристика
1
C
b ( )
( ) arctg
arctg L
g
g
Амплитудно-частотные характеристики – это зависимости
действующих или амплитудных значений тока от
частоты:
I ( )
I 1 ( )
I 2 ( )

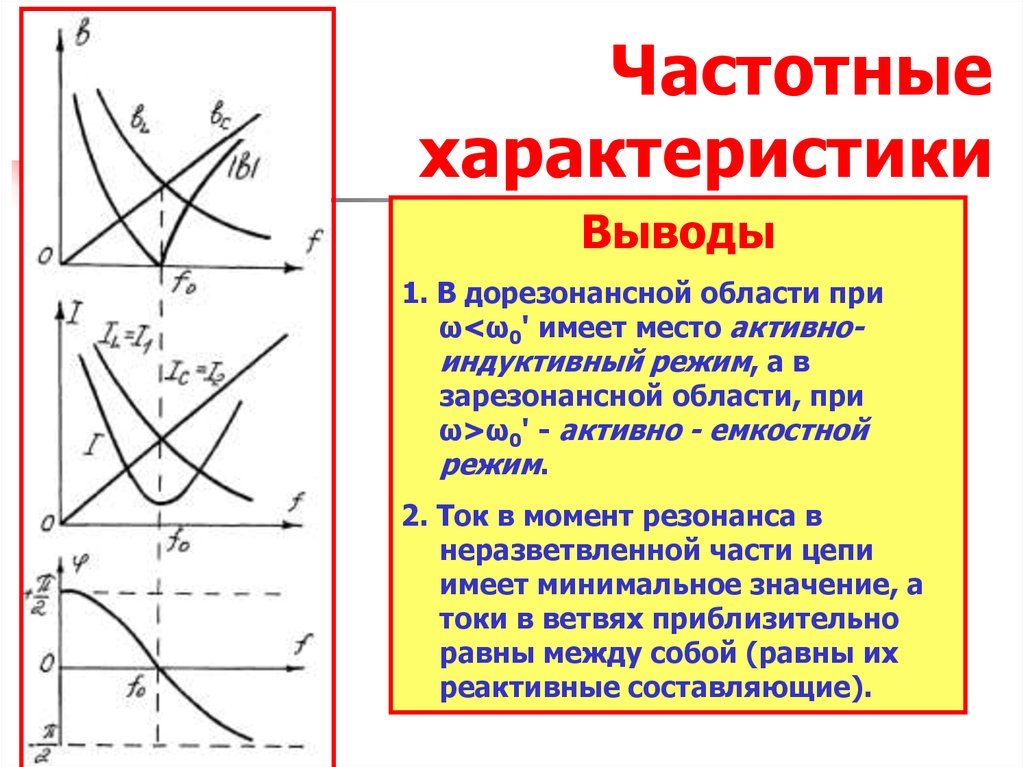
37. Частотные характеристики

Выводы
1. В дорезонансной области при
ω<ω0' имеет место активноиндуктивный режим, а в
зарезонансной области, при
ω>ω0' - активно - емкостной
режим.
2. Ток в момент резонанса в
неразветвленной части цепи
имеет минимальное значение, а
токи в ветвях приблизительно
равны между собой (равны их
реактивные составляющие).