Similar presentations:
Частотные свойства цепей синусоидального тока. Резонанс токов. Лекция №12
1. Дисциплина: Теоретические основы электротехники
2.
23. Лекция №12
Тема: Частотныесвойства цепей
синусоидального
тока. Резонанс токов
4. Учебные вопросы
1. Понятие о резонансе впараллельном колебательном
контуре.
2. Свойства цепи при резонансе
токов.
3. Частотные характеристики
параллельного колебательного
контура.
4. Применение явления резонанса в
электрических цепях.
5. Литература
1. Бессонов Л.А.Теоретические основы
электротехники.
Электрические цепи:
учебник для бакалавров. –
М. : Издательство Юрайт,
2012, с. 106-114.
6.
1. Понятие о резонансе в параллельномколебательном контуре
Избирательностью (селективностью) называется
свойство цепи пропускать на выход из всей суммы
колебаний различных частот только колебания с
относительно узкой полосой частот.
Избирательность параллельных колебательных
контуров основана на явлении резонанса токов.
Резонансом называется режим работы
электрической цепи, содержащей участки
индуктивного и емкостного характера, при котором
разность фаз между напряжением и током на входе
цепи равна нулю.
Резонансом токов называется явление резонанса в
участке электрической цепи, содержащей
параллельно соединенные индуктивный и емкостной элементы.
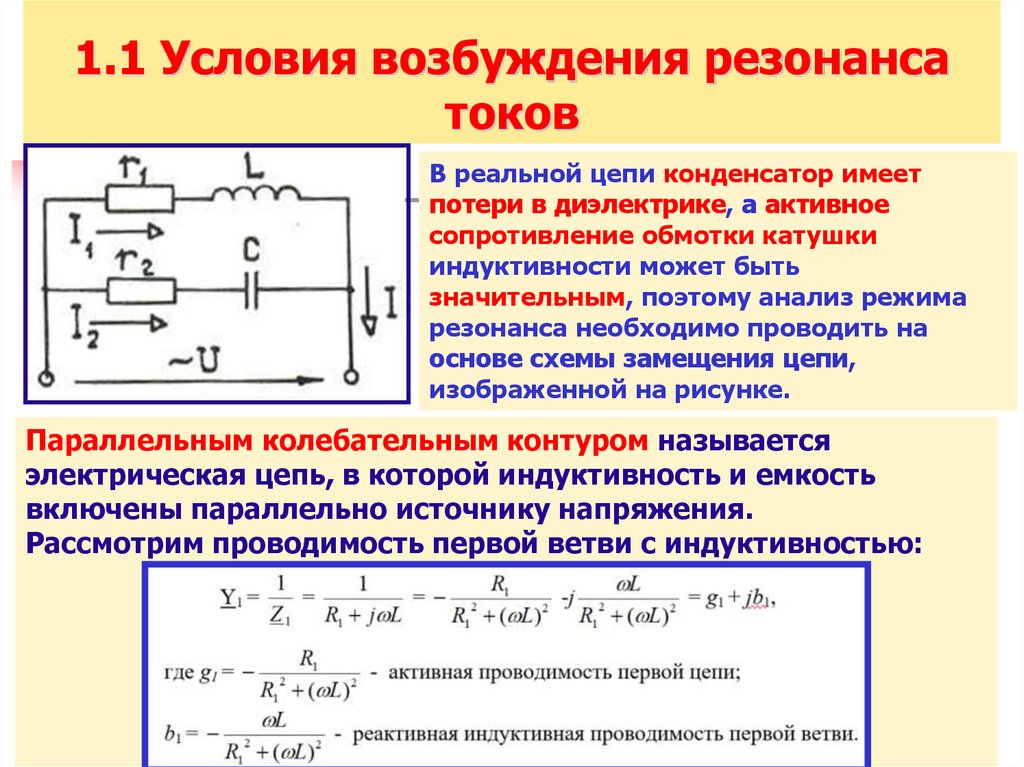
7. 1.1 Условия возбуждения резонанса токов
В реальной цепи конденсатор имеетпотери в диэлектрике, а активное
сопротивление обмотки катушки
индуктивности может быть
значительным, поэтому анализ режима
резонанса необходимо проводить на
основе схемы замещения цепи,
изображенной на рисунке.
Параллельным колебательным контуром называется
электрическая цепь, в которой индуктивность и емкость
включены параллельно источнику напряжения.
Рассмотрим проводимость первой ветви с индуктивностью:
8. Условия возбуждения резонанса токов (продолжение)
Рассмотрим проводимость второйветви с конденсатором:
9. Условия возбуждения резонанса токов (окончание)
По определению резонансного режима ток I должен совпадатьпо фазе с напряжением U, т.е. φ = ψu – ψi = 0. Это будет и при
условии, что сумма реактивных проводимостей ветвей равна
нулю: b1 + b2 = 0.
Следовательно, условием возбуждения резонанса токов
является равенство индуктивной и емкостной проводимостей:
Резонансную угловую частоту можно получить из
приведённого выше уравнения, разрешив его
относительно ωʹ0.
10. 1.2 Резонансная частота и способы возбуждения резонанса токов
Вывод: резонанса токов можно добиться теми же способами,которыми обеспечивается резонанс напряжений:
изменением частоты приложенного к цепи напряжения ω
или собственной резонансной частоты ω0', т.е. на основе
равенства ω=ω0'.
11.
2. Свойства цепи прирезонансе токов
Рассмотрим эти свойства при небольшом
упрощении, приняв R2 = 0, т.е. считая,
что потери энергии в конденсаторе
невелики. Схема замещения цепи
примет вид, показанный на рисунке.
b 0 L b 0C
y Y g 2 (bC bL ) 2
b0 b0L b0C 0
Несмотря на наличие
индуктивности L и
емкости C, цепь по
отношению к
источнику ведет
себя как резистор с
проводимостью g0.
12.
Свойства цепи при резонансетоков (продолжение)
2. Ток в цепи при резонансе токов является
минимальным и по характеру чисто активным,
т.е. не имеет сдвига по фазе по отношению к
напряжению:
b 0C b 0 L
b0
0 u i arctg
arctg
0
g0
g0
13.
Свойства цепи при резонансе токов3. Коэффициент мощности цепи равен единице, полная
мощность равна активной, следовательно, ток в цепи при
резонансе совершает максимально полезную работу.
cos(φ0)=1; P0=UI0=S0
4. В цепи имеют место колебания энергии электрического и
магнитного полей конденсатора и катушки, при этом скорости
взаимного преобразования энергии этих полей одинаковы (Q0L
= Q0C), к источнику энергия не возвращается (Q0 = 0).
Энергетический процесс при резонансе токов, если сопротивление R1
мало, протекает аналогично процессу в цепи при резонансе
напряжений ( ω0'≈ω0): источник питания лишь доставляет энергию в
цепь на покрытие ее тепловых потерь. В конденсаторе и катушке
имеют место взаимные преобразования энергии электрического и
магнитного полей, происходящее с двойной частотой по сравнению с
14.
Свойства цепи прирезонансе токов
5. Действующие значения токов ветвей контура на
резонансной частоте одинаковы:
U
I 0 L I 0C Ub0 L Ub0C I 0
R1
так как
6. Добротность параллельного
колебательного контура совпадает с
добротностью последовательного контура,
составленного из тех же элементов.
15. 3. Частотные характеристики параллельного колебательного контура
Зависимости от частоты параметров контура:b ( ) b L ( ) bC ( )
Фазо-частотная
характеристика
1
C
b ( )
( ) arctg
arctg L
g
g
Амплитудно-частотные характеристики токов (резонансные
характеристики)– это зависимости действующих или
амплитудных значений тока от частоты:
I ( )
I 1 ( )
I 2 ( )
16.
Построение резонансныххарактеристик токов ведется в
действующих значениях на основе
следующих соотношений:
17. Частотные характеристики параллельного колебательного контура
Выводы1.
Ток в момент резонанса в
неразветвленной части цепи имеет
минимальное значение, а токи в
ветвях приблизительно равны между
собой (равны их реактивные
составляющие).
2. В дорезонансной области при
ω<ω0' имеет место активноиндуктивный режим, а в
зарезонансной области, при
ω>ω0' - активно - емкостной
режим.
3. Максимальный сдвиг фаз между
напряжением и током наблюдается
при минимальных и при
максимальных частотах.
18.
4. Применение явления резонанса в электрическихцепях. 4.1 Применение резонанса напряжений
1. Явление резонанса напряжений используют в электрических
фильтрах разного рода.
Если необходимо пропустить только ток определенной частоты, то LC-цепочку
включают последовательно приемнику, тогда составляющие сигнала на
резонансной частоте цепочки пройдут к нагрузке почти без потерь, а частоты
далекие от резонанса окажутся сильно ослаблены и можно сказать, что к нагрузке
совсем не попадут. Данный принцип применим к радиоприемникам, где
перестраиваемый колебательный контур настраивают на прием строго
определенной частоты нужной радиостанции.
Или наоборот, если необходимо устранить из передаваемого сигнала
составляющую тока определенной частоты, то параллельно приемнику ставят
цепочку из соединенных последовательно конденсатора и катушки
индуктивности, чтобы ток резонансной частоты этой LC-цепочки замкнулся бы
через нее, и не попал к бы приемнику. Тогда токи частоты далекой от резонансной
частоты LC-цепочки будут проходить в нагрузку беспрепятственно, и только
близкие к резонансу по частоте токи - будут находить себе кротчайший путь через
LC-цепочку.
19.
Применение резонанса напряжений2. Явление резонанса напряжений используют для стабилизации
напряжения. Если напряжение в сети непредсказуемо упало, а станку
нужно напряжение не менее 220 вольт, то последовательно со станком
(если приводом в нем является асинхронный двигатель) включают по
несколько конденсаторов на фазу, и таким образом напряжение на
обмотках статора поднимается.
Здесь важно правильно подобрать количество конденсаторов, чтобы
они точно скомпенсировали своим емкостным сопротивлением вместе с
индуктивным сопротивлением обмоток просадку напряжения в сети, то
есть слегка приблизив цепь к резонансу — можно поднять упавшее
напряжение даже под нагрузкой.
3. Резонанс напряжений в электротехнике является нежелательным
явлением, поскольку он вызывает перенапряжения и выход из строя
оборудования. Например, возьмем длинную кабельную линию, которая
по какой-то причине оказалась не подключенной к нагрузке, но при
этом питается от промежуточного трансформатора. Такая линия с
распределенной емкостью и индуктивностью, если ее резонансная
частота совпадет с частотой питающей сети, просто будет пробита и
выйдет из строя. Чтобы предотвратить разрушение кабелей от
случайного резонанса напряжений, применяют вспомогательную
нагрузку.
20.
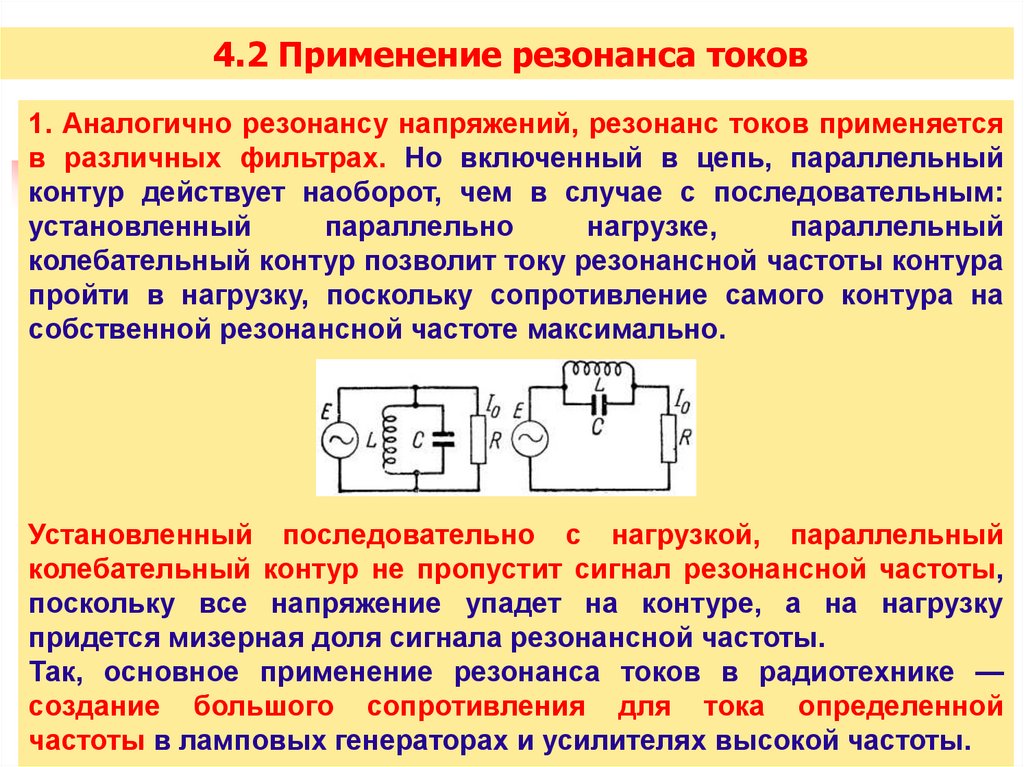
4.2 Применение резонанса токов1. Аналогично резонансу напряжений, резонанс токов применяется
в различных фильтрах. Но включенный в цепь, параллельный
контур действует наоборот, чем в случае с последовательным:
установленный
параллельно
нагрузке,
параллельный
колебательный контур позволит току резонансной частоты контура
пройти в нагрузку, поскольку сопротивление самого контура на
собственной резонансной частоте максимально.
Установленный последовательно с нагрузкой, параллельный
колебательный контур не пропустит сигнал резонансной частоты,
поскольку все напряжение упадет на контуре, а на нагрузку
придется мизерная доля сигнала резонансной частоты.
Так, основное применение резонанса токов в радиотехнике —
создание большого сопротивления для тока определенной
частоты в ламповых генераторах и усилителях высокой частоты.
21.
Применение резонанса токов2. В электротехнике резонанс токов используется с целью
достижения высокого коэффициента мощности нагрузок,
обладающих значительными индуктивными и емкостными
составляющими.
Например, установки компенсации реактивной мощности
(КРМ) представляют собой конденсаторы, подключаемые
параллельно обмоткам асинхронных двигателей и
трансформаторов, работающих под нагрузкой ниже
номинальной.
К таким решениям прибегают как раз с целью достижения
резонанса токов (параллельного резонанса), когда
индуктивное сопротивление оборудования делается равным
емкостному сопротивлению подключаемых конденсаторов
на частоте сети, чтобы реактивная энергия циркулировала
между конденсаторами и оборудованием, а не между
оборудованием и сетью; чтобы сеть отдавала энергию
только тогда, когда оборудование нагружено и потребляет
активную мощность.



















 physics
physics








