Четырехмерный мир (пространство Минковского)

1.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Определение 1:
R (ct, x, y, z )
четырехвектор события (мировой точки)
R 2 c 2t 2 x 2 y 2 z 2
квадрат длины
Компоненты R преобразуются в соответствии с преобразованиями Лоренца
Определение 2:
Четырехскаляром (инвариантом) называется величина, не зависящая от
выбора ИСО a a
R2
четырехскаляр

2.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Определение 3:
A ( At , Ax , Ay , Az ) четырехвектор
Компоненты A преобразуются в соответствии с преобразованиями Лоренца
Ax ( Ax At )
A y Ay
Ax ( Ax At )
Ay A y
Az Az
At ( At Ax )
Az Az
1 1 2 ,
At ( At Ax )
V c

3.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Свойства четырехвекторов
A2 At2 Ax2 Ay2 Az2
1.
A2 inv
2.
A B
квадрат длины четырехвектора
четырехскаляр
A B
Равенство четырехвекторов сохраняется во всех ИСО
Четырехвектора можно складывать и умножать на числа как и обычные векторы.
Типы четырехвекторов
1.
A2 0
пространственноподобный
2.
A2 0
времениподобный
3.
A2 0
светоподобный

4.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Четырехскорость
V
dR
d
, собственное время материальной точки
dt d
V
1
dR
( c, v x , v y , vz )
dt
1 2 , v c
или
V ( c, v)
V 2 2c2 2v2 2c2 (1 v2 c2 ) c 2

5.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Релятивистский закон сложения скоростей
Из преобразований Лоренца для четырехскорости
v x
vx V
,
1 vx c
v y
При малых скоростях
v x v x V ,
v y v y ,
V
vy
(1 vx c)
c, v
v z vz
,
v z
vz
(1 vx c)
c
или
v v V
Релятивистский закон сложения скоростей соответствуют второму
постулату Эйнштейна о неизменности скорости света c во всех ИСО.

6.

Релятивистская динамика
Нерелятивистский импульс
Если в результате столкновения шаров (тел) движение одного шара
"уменьшилось", то движение другого шара "увеличилось".
Поэтому предполагается, что при соударении тел сумма мер движения
шаров не меняется.
Закон сохранения импульса (для замкнутых систем)
p
i
const,
pi mi vi
Следствия:
1. Закон сохранения массы.
2. Закон сохранение кинетической энергии при абсолютно упругих
столкновениях

7.

Релятивистская динамика
Релятивистский импульс
Пусть в релятивистском случае
1.
2.
p
i
const
p m( v )v
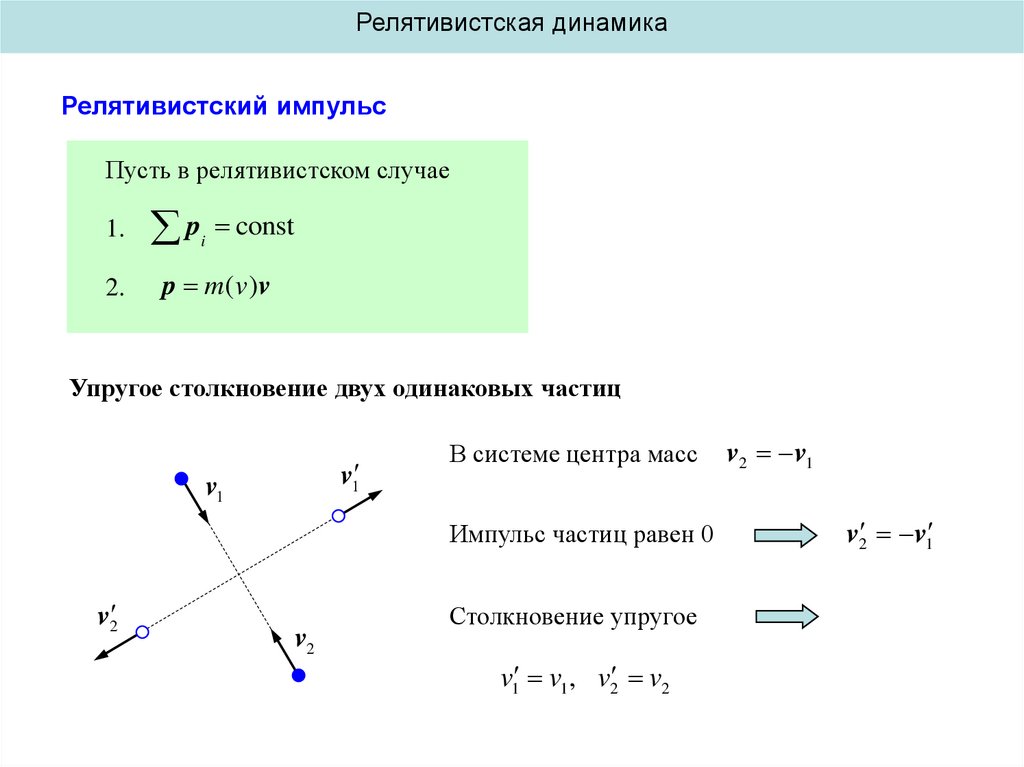
Упругое столкновение двух одинаковых частиц
v1
v1
В системе центра масс
Импульс частиц равен 0
v2
v2
Столкновение упругое
v1 v1 , v2 v2
v2 v1
v2 v1

8.

Релятивистская динамика
Релятивистский импульс
4-импульс
P mV ( mc, mv)
m обычная масса
при
v 0
mv mv
В системе центра масс
P1 P2 P1 P2
4-вектор
(2 mc,0,0,0) (2 mc,0,0,0)
4-вектор
данное равенство сохраняется во всех ИСО

9.

Релятивистская динамика
Релятивистский импульс
P1 P2 P1 P2
или
( 1mc 2mc, 1mv1 2mv2 ) ( 1 mc 2mc, 1 mv1 2mv2 )
p1 p2 const
p mv
релятивистский импульс
Данное выражение импульса единственное совместимое с
принципом сохранения импульса при столкновении двух частиц
p
i
const, p mv
закон сохранения импульса

10.

Релятивистская динамика
Релятивистский энергия
Определение:
E mc 2
релятивистский энергия
4-импульс системы
Ei
,
m
v
i i i
c
Так как в замкнутой системе во всех ИСО сохраняются
пространственные компоненты 4-импульса системы
Сохраняется также временная компонента 4-импульса системы, или
E
i
const, E mc2
закон сохранения энергии

11.

Релятивистская динамика
Релятивистский энергия
При малых скоростях
E0 mc 2
2
mv
E mc 2 mc 2
2
энергия покоя
K E E0 ( 1)mc 2
кинетическая энергия
При упругих столкновениях
K
i
const
Таким образом, закон сохранения импульса приводит к
закону сохранения энергии и к
закону сохранения кинетической энергии (для упругих столкновений)

12.

Релятивистская динамика
Релятивистский энергия
4-вектор энергии-импульса (4-импульса)
E
P ,
c
p
P 2 E 2 c 2 p 2 m2c 2
Энергия и импульс света
При v = c
pc 2
E
v
E pc
E 2 c 2 p 2 m 2c 2 0
m 0
Данные соотношения подтверждаются экспериментально,
например, при изучении эффекта Комптона.

13.

Релятивистская динамика
Релятивистская сила
E c p m c
dE
dp
v
dt
dt
L r p
dL
dp
r
dt
dt
2
d
dt
2
2
2 2
Исходя их этого, сила (как мера воздействия) определяется как
F
dp
dt
4-вектор силы
F
dP
d
dt d
dE
vF
dt

14.

Релятивистская динамика
Релятивистская сила
F ( Fv ), F
c
В соответствии с преобразованиями Лоренца
B
( Fv )
c
Fx
,
1 v x c
Fx
F v
Fv VFx
,
1 v x c
Fy
Fy
(1 v x c )
,
Fz
Fz
(1 v x c )