Механика

1.

Литература:
Трофимова Т.И. – Курс Физики
Савельев И.В. – Курс физики, том 1 – Механика и Молекулярная Физика
Савченко Н.Е. – Решение задач по физике
Фирганг Е.В. - Руководство к решению задач по курсу общей физике
1

2.

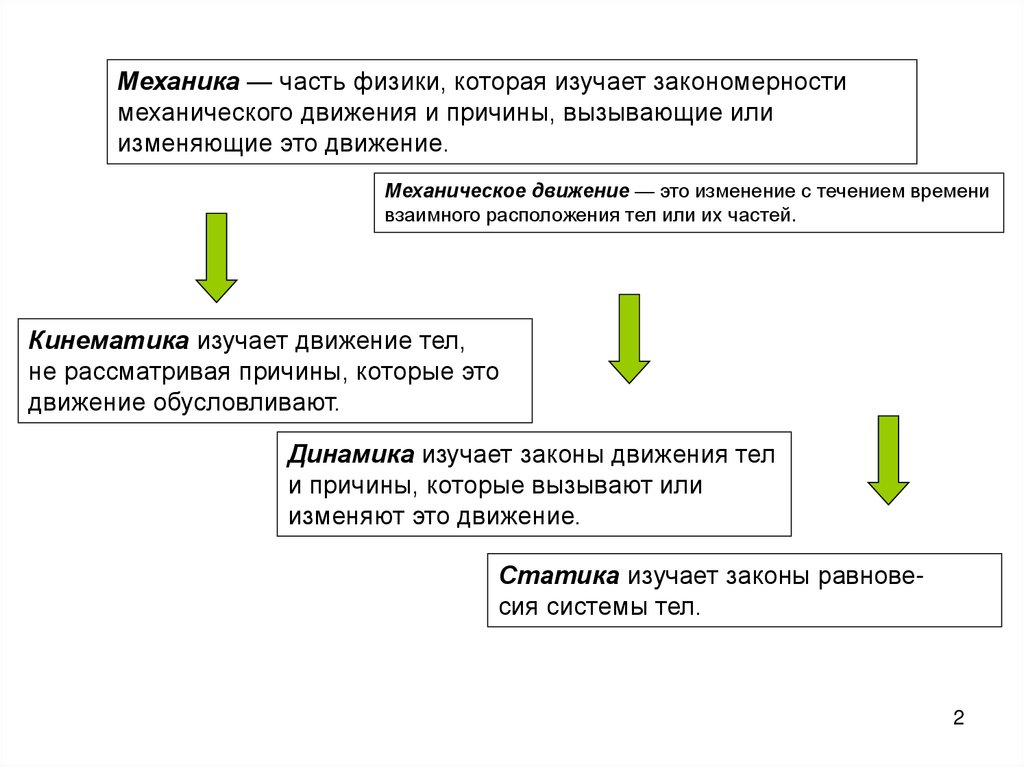
Механика — часть физики, которая изучает закономерности
механического движения и причины, вызывающие или
изменяющие это движение.
Механическое движение — это изменение с течением времени
взаимного расположения тел или их частей.
Кинематика изучает движение тел,
не рассматривая причины, которые это
движение обусловливают.
Динамика изучает законы движения тел
и причины, которые вызывают или
изменяют это движение.
Статика изучает законы равновесия системы тел.
2

3.

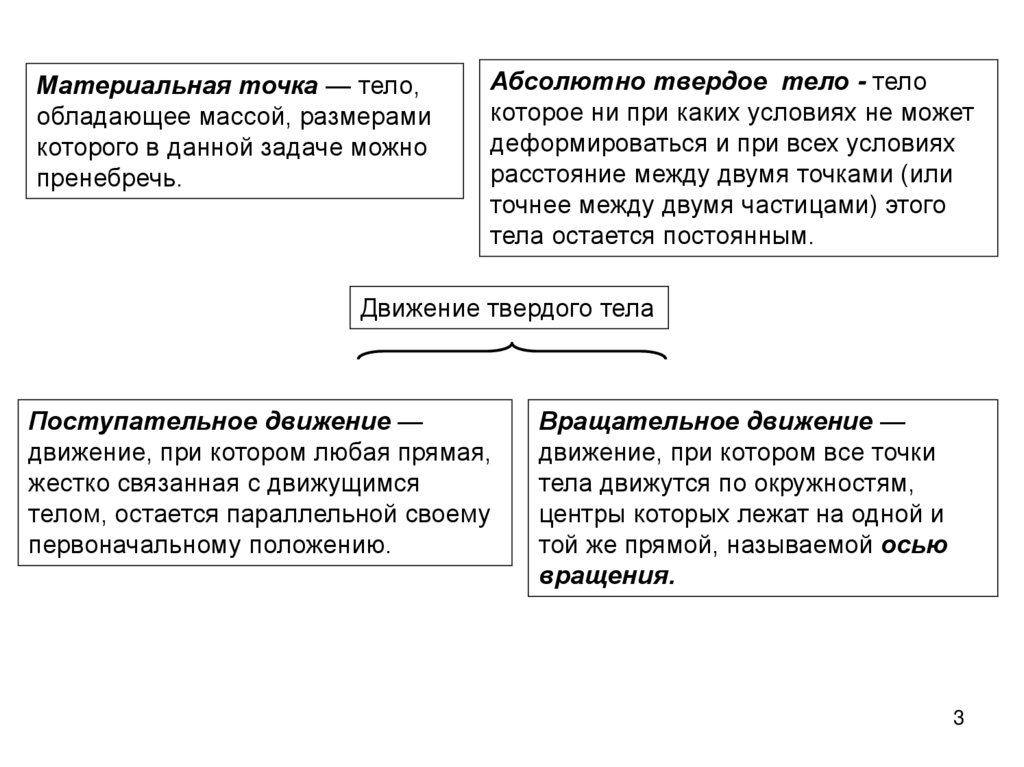
Материальная точка — тело,
обладающее массой, размерами
которого в данной задаче можно
пренебречь.
Абсолютно твердое тело - тело
которое ни при каких условиях не может
деформироваться и при всех условиях
расстояние между двумя точками (или
точнее между двумя частицами) этого
тела остается постоянным.
Движение твердого тела
Поступательное движение —
движение, при котором любая прямая,
жестко связанная с движущимся
телом, остается параллельной своему
первоначальному положению.
Вращательное движение —
движение, при котором все точки
тела движутся по окружностям,
центры которых лежат на одной и
той же прямой, называемой осью
вращения.
3

4.

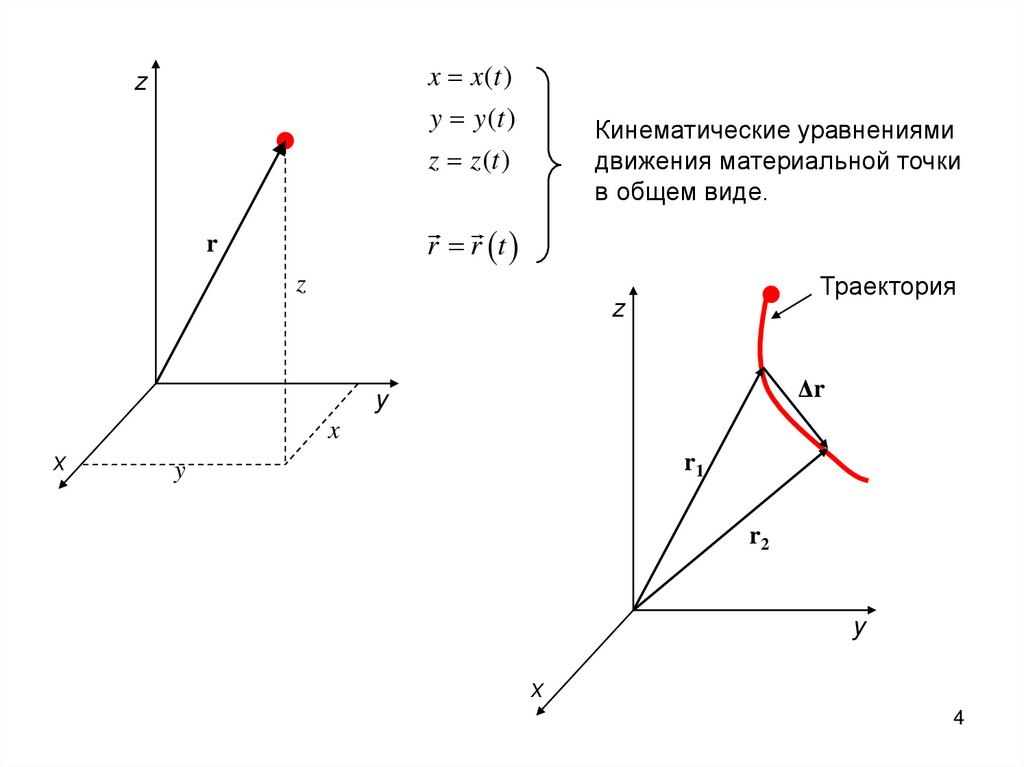
x x (t )
y y (t )
z z (t )
z
Кинематические уравнениями
движения материальной точки
в общем виде.
r r t
r
Траектория
z
z
Δr
y
x
х
r1
y
r2
y
х
4

5.

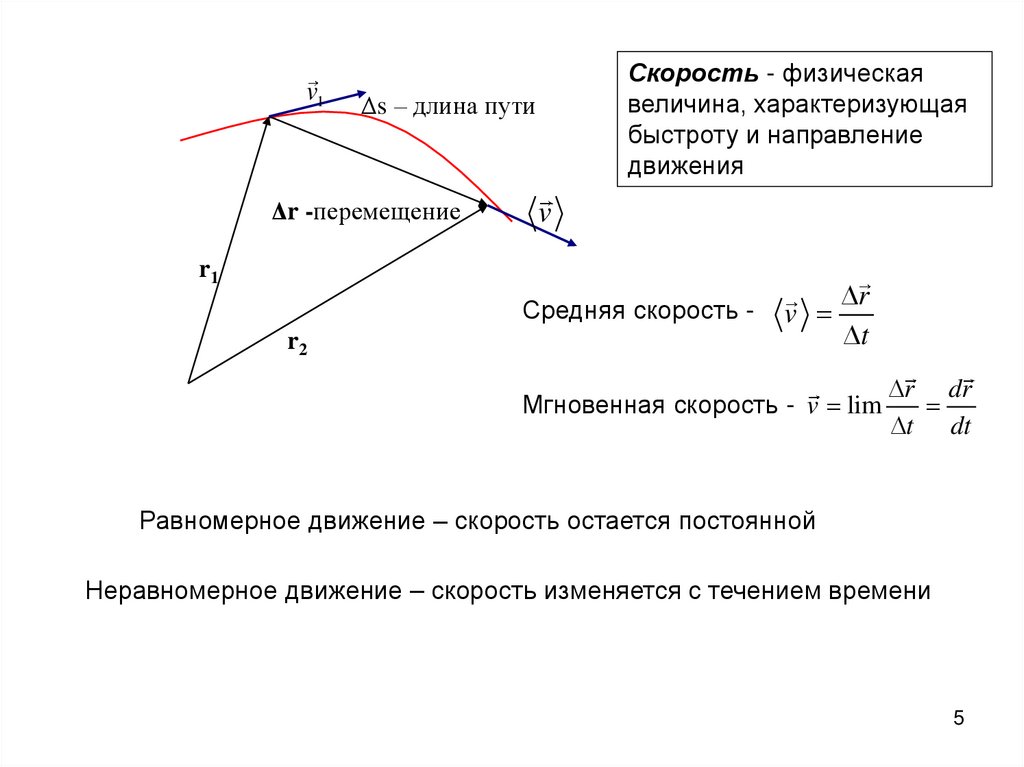
v1
Скорость - физическая
величина, характеризующая
быстроту и направление
движения
Δs – длина пути
Δr -перемещение
v
r1
Средняя скорость -
v
r2
r
t
Мгновенная скорость - v lim
r dr
t dt
Равномерное движение – скорость остается постоянной
Неравномерное движение – скорость изменяется с течением времени
5

6.

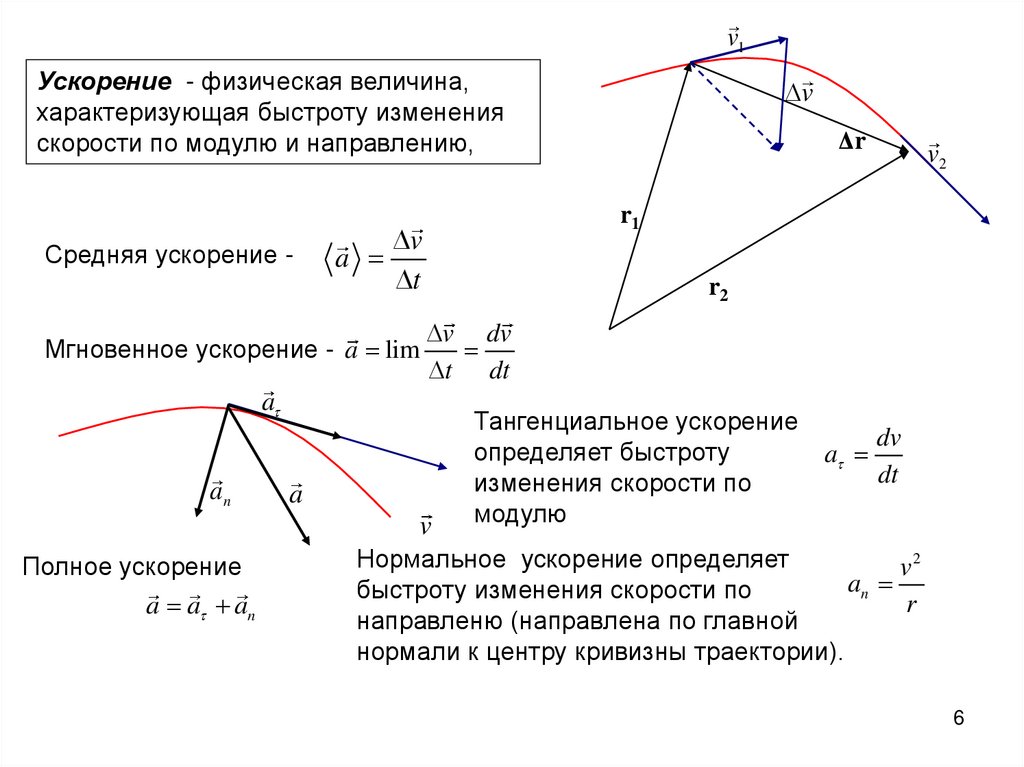
v1
Ускорение - физическая величина,
характеризующая быстроту изменения
скорости по модулю и направлению,
Средняя ускорение -
v dv
t dt
a
v
Полное ускорение
a a an
v2
r2
a
an
Δr
r1
v
a
t
Мгновенное ускорение - a lim
v
Тангенциальное ускорение
определяет быстроту
изменения скорости по
модулю
a
dv
dt
Нормальное ускорение определяет
v2
an
быстроту изменения скорости по
r
направленю (направлена по главной
нормали к центру кривизны траектории).
6

7.

Кинематические уравнения движения материальной точки
Прямолинейное равномерное движение
ax 0 v const
x x0 vt
Прямолинейное равнопеременное движение
ax const
vx v0 x axt
at 2
x x0 v0 xt
2
ax 0
- равноускоренное движение
ax 0
- равнозамедленное движение
7

8.

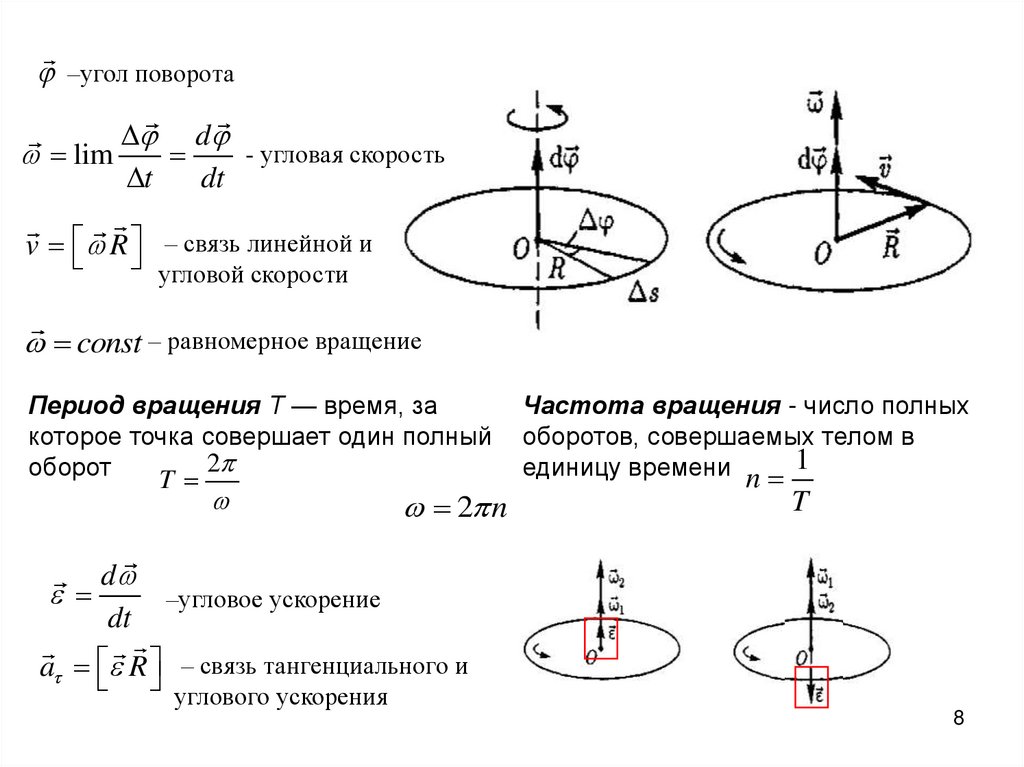
–угол поворота
d
- угловая скорость
lim
t
dt
v R – связь линейной и
угловой скорости
const – равномерное вращение
Период вращения Т — время, за
которое точка совершает один полный
2
оборот
T
2 n
Частота вращения - число полных
оборотов, совершаемых телом в
единицу времени n 1
T
d
–угловое ускорение
dt
a R – связь тангенциального и
углового ускорения
8

9.

Первый закон Ньютона: всякая материальная точка (тело) сохраняет
состояние покоя или равномерного прямолинейного движения до тех пор,
пока воздействие со стороны других тел не заставит ее изменить это
состояние.
Инертность - стремление
тела сохранять состояние покоя
или равномерного
прямолинейного движения.
первый закон Ньютона - закон инерции
Те системы отсчета, по отношению к которым выполняется первый закон
Ньютона, называются инерциальными системами отсчета.
Относительно таких систем материальная точка, свободная от внешних
воздействий, либо покоится, либо движется равномерно и прямолинейно.
Масса тела — физическая
величина, одна из основных
характеристик материи,
определяющая ее инерционные
(инертная масса) и гравитационные
(гравитационная масса) свойства.
Сила — это векторная величина,
мера механического воздействия
на тело со стороны других тел или
полей, в результате которого тело
приобретает ускорение или
изменяет свою форму и размеры.
9

10.

Второй закон Ньютона — основной закон динамики поступательного
движения — отвечает на вопрос, как изменяется механическое движение
материальной точки (тела) под действием приложенных к ней сил.
Второй закон Ньютона: ускорение, приобретаемое материальной
точкой (телом), пропорционально вызывающей его силе, совпадает с
нею по направлению и обратно пропорционально массе материальной
точки (тела).
a
F
m
Импульс (количество движения) – векторная величина численно равная
произведению массы материальной точки на ее скорость и имеющая
направление скорости
p mv
dp dp
F F
dt dt
Более общая формулировка второго закона
Ньютона: скорость изменения импульса материальной
точки равна действующей на нее силе.
Принцип независимости действия сил: если на материальную
точку действует одновременно несколько сил, то каждая из этих сил
сообщает материальной точке ускорение согласно второму закону
Ньютона, как будто других сил не было
10

11.

Взаимодействие между материальными точками (телами) определяется
третьим законом Ньютона: всякое действие материальных точек (тел)
друг на друга носит характер взаимодействия; силы, с которыми действуют
друг на друга материальные точки, всегда равны по модулю, противоположно
направлены и действуют вдоль прямой, соединяющей эти точки. Эти силы
приложены к разным материальным точкам (телам), всегда действуют
парами и являются силами одной природы.
F12
F12
F12 F21
Все три законы Ньютона, справедливы
только в инерциальных системах отсчета
11

12.

Совокупность материальных
точек (тел), рассматриваемых
как единое целое, называется
механической системой.
Силы взаимодействия между
материальными точками механической
системы называются внутренними.
Силы, с которыми на материальные
точки системы действуют внешние
тела, называются внешними
Механическая система тел, на
которую не действуют внешние
силы, называется замкнутой
(или изолированной).
Закон сохранения импульса: импульс
замкнутой системы сохраняется, т. е. не
изменяется с течением времени
p mi vi const
i
Центром масс (или центром инерции)
системы материальных точек называется
воображаемая точка С, положение которой
характеризует распределение массы этой
системы.
i mi vi p mvC
i mi ri
vC
rC
m
m
Закон движения центра масс
m
dvC
F1 F2
dt
Fn
12

13.

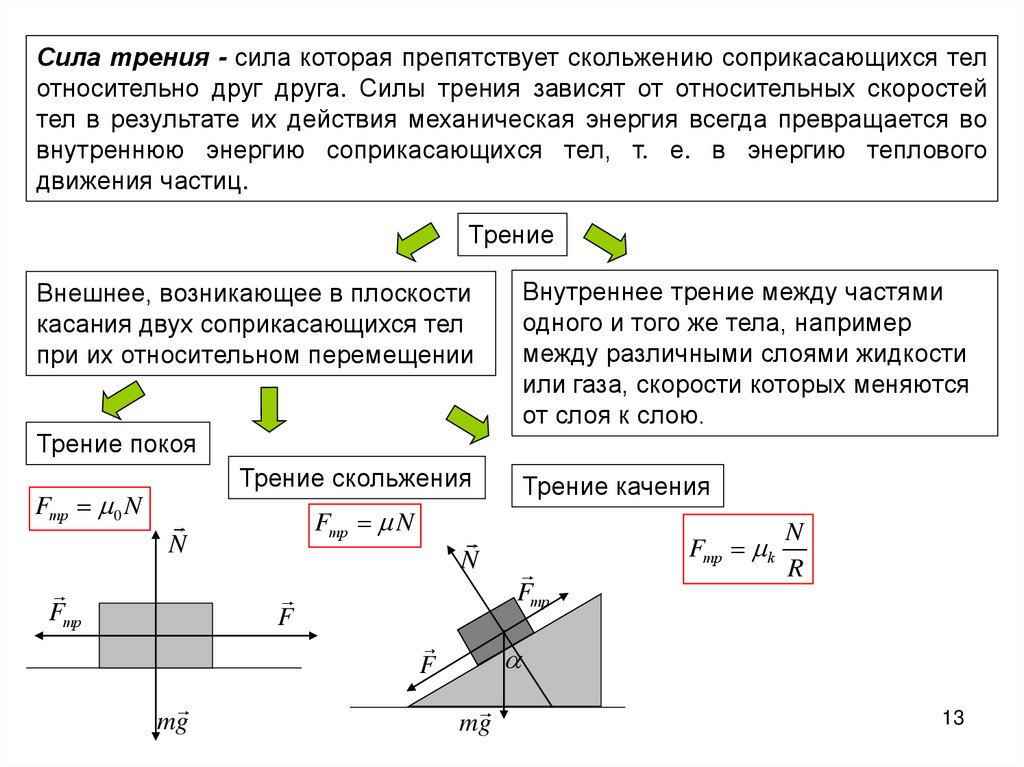
Сила трения - сила которая препятствует скольжению соприкасающихся тел
относительно друг друга. Силы трения зависят от относительных скоростей
тел в результате их действия механическая энергия всегда превращается во
внутреннюю энергию соприкасающихся тел, т. е. в энергию теплового
движения частиц.
Трение
Внутреннее трение между частями
одного и того же тела, например
между различными слоями жидкости
или газа, скорости которых меняются
от слоя к слою.
Внешнее, возникающее в плоскости
касания двух соприкасающихся тел
при их относительном перемещении
Трение покоя
Трение скольжения
Fтр 0 N
Fтр N
N
Fтр
Fтр k
N
Fтр
F
N
R
F
mg
Трение качения
mg
13

14.

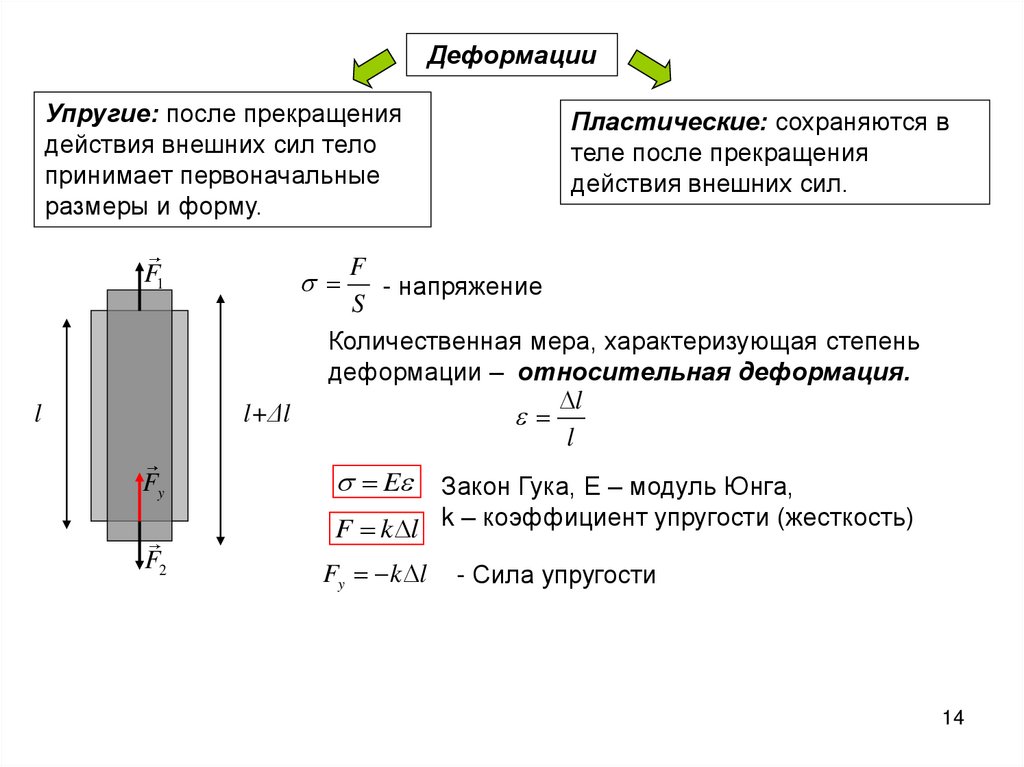
Деформации
Упругие: после прекращения
действия внешних сил тело
принимает первоначальные
размеры и форму.
F1
l
Пластические: сохраняются в
теле после прекращения
действия внешних сил.
F
- напряжение
S
Количественная мера, характеризующая степень
деформации – относительная деформация.
l
l
l+Δl
E
Fy
Закон Гука, Е – модуль Юнга,
F k l k – коэффициент упругости (жесткость)
F2
Fy k l
- Сила упругости
14

15.

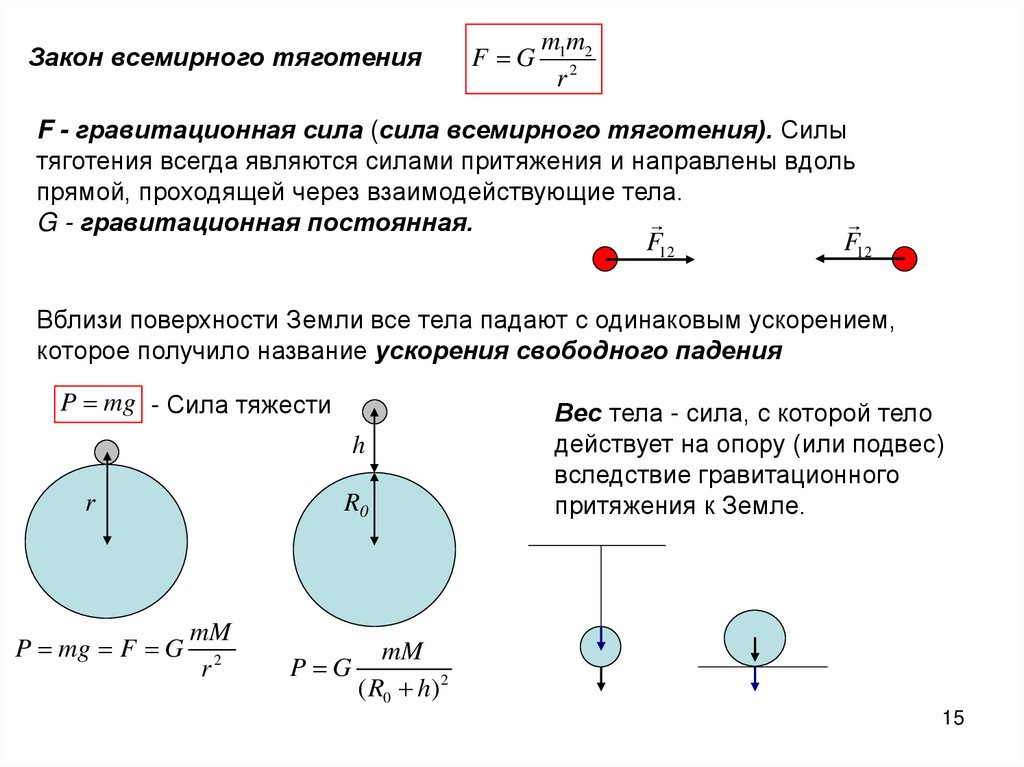
Закон всемирного тяготения
F G
m1m2
r2
F - гравитационная сила (сила всемирного тяготения). Силы
тяготения всегда являются силами притяжения и направлены вдоль
прямой, проходящей через взаимодействующие тела.
G - гравитационная постоянная.
F12
F12
Вблизи поверхности Земли все тела падают с одинаковым ускорением,
которое получило название ускорения свободного падения
P mg - Сила тяжести
h
r
P mg F G
R0
mM
r2
P G
Вес тела - сила, с которой тело
действует на опору (или подвес)
вследствие гравитационного
притяжения к Земле.
mM
( R0 h) 2
15

16.

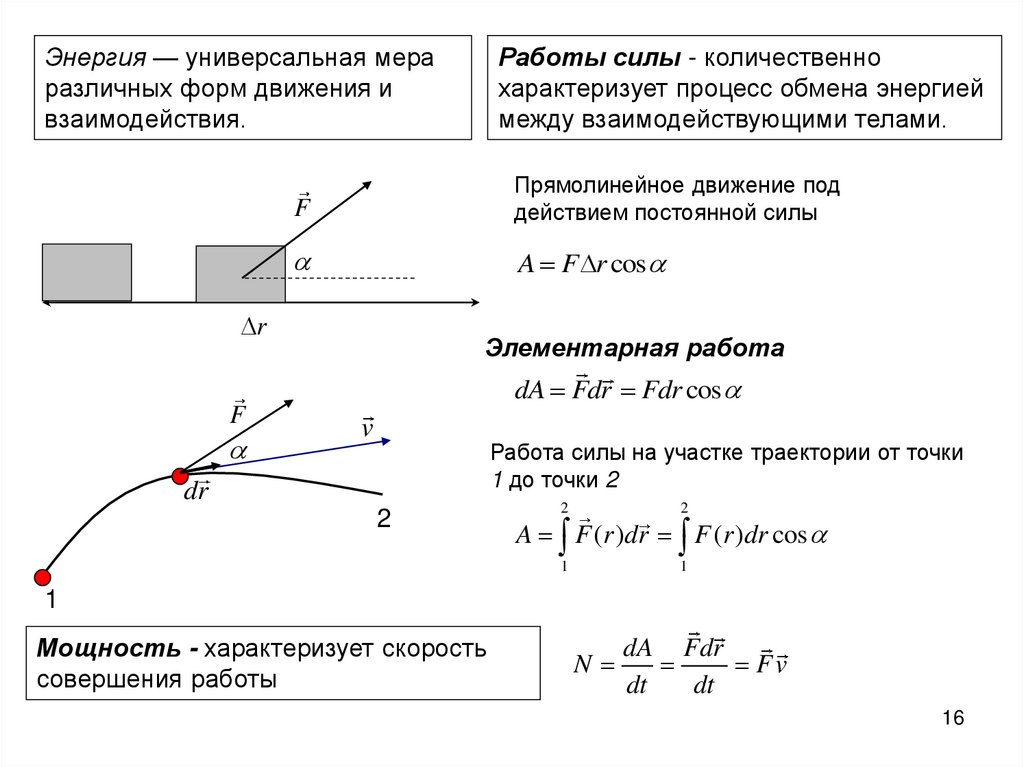
Энергия — универсальная мера
различных форм движения и
взаимодействия.
Работы силы - количественно
характеризует процесс обмена энергией
между взаимодействующими телами.
F
Прямолинейное движение под
действием постоянной силы
A F r cos
r
Элементарная работа
dA Fdr Fdr cos
F
v
Работа силы на участке траектории от точки
1 до точки 2
dr
2
2
2
1
1
A F (r )dr F (r )dr cos
1
Мощность - характеризует скорость
совершения работы
N
dA Fdr
Fv
dt
dt
16

17.

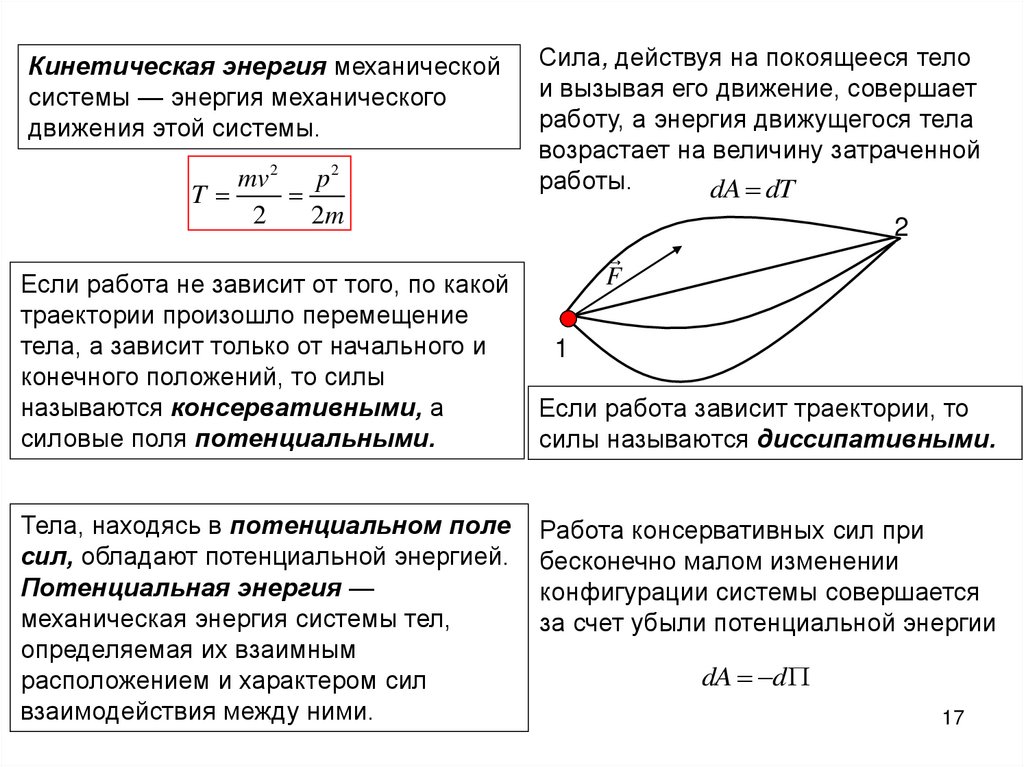
Кинетическая энергия механической
системы — энергия механического
движения этой системы.
mv 2 p 2
T
2
2m
Если работа не зависит от того, по какой
траектории произошло перемещение
тела, а зависит только от начального и
конечного положений, то силы
называются консервативными, а
силовые поля потенциальными.
Тела, находясь в потенциальном поле
сил, обладают потенциальной энергией.
Потенциальная энергия —
механическая энергия системы тел,
определяемая их взаимным
расположением и характером сил
взаимодействия между ними.
Сила, действуя на покоящееся тело
и вызывая его движение, совершает
работу, а энергия движущегося тела
возрастает на величину затраченной
работы.
dA dT
2
F
1
Если работа зависит траектории, то
силы называются диссипативными.
Работа консервативных сил при
бесконечно малом изменении
конфигурации системы совершается
за счет убыли потенциальной энергии
dA d
17

18.

Для консервативных сил
Fx
, Fy
, Fz
F grad
x
y
z
Конкретный вид функции потенциальной энергии зависит от
характера силового поля
mgh
h
П=0
r
G
Δl
m1m2
r
k ( l ) 2
2
потенциальная энергия тела поднятого над
поверхностью Земли (h<<R0)
потенциальная энергия гравитационного
взаимодействия
потенциальная энергия
упругодеформированного тела
Полная механическая энергия системы — энергия механического движения
и взаимодействия, равна сумме кинетической и потенциальной энергий
E T
18

19.

Закон сохранения механической энергии: в системе тел, между которыми
действуют только консервативные силы, полная механическая энергия
сохраняется, т. е. не изменяется со временем.
E T const
Механические системы, на тела которых действуют только консервативные
силы (внутренние и внешние), называются консервативными системами.
Закон сохранения механической энергии можно сформулировать
так: в консервативных системах полная механическая энергия сохраняется.
диссипативные системы –
системы, в которых механическая
энергия постепенно уменьшается за
счет преобразования в другие
(немеханические) формы энергии.
Этот процесс получил название
диссипации (рассеяния) энергии.
Закон сохранения и превращения энергии: энергия никогда не
исчезает и не появляется вновь, она лишь превращается из одного
вида в другой.
19

20.

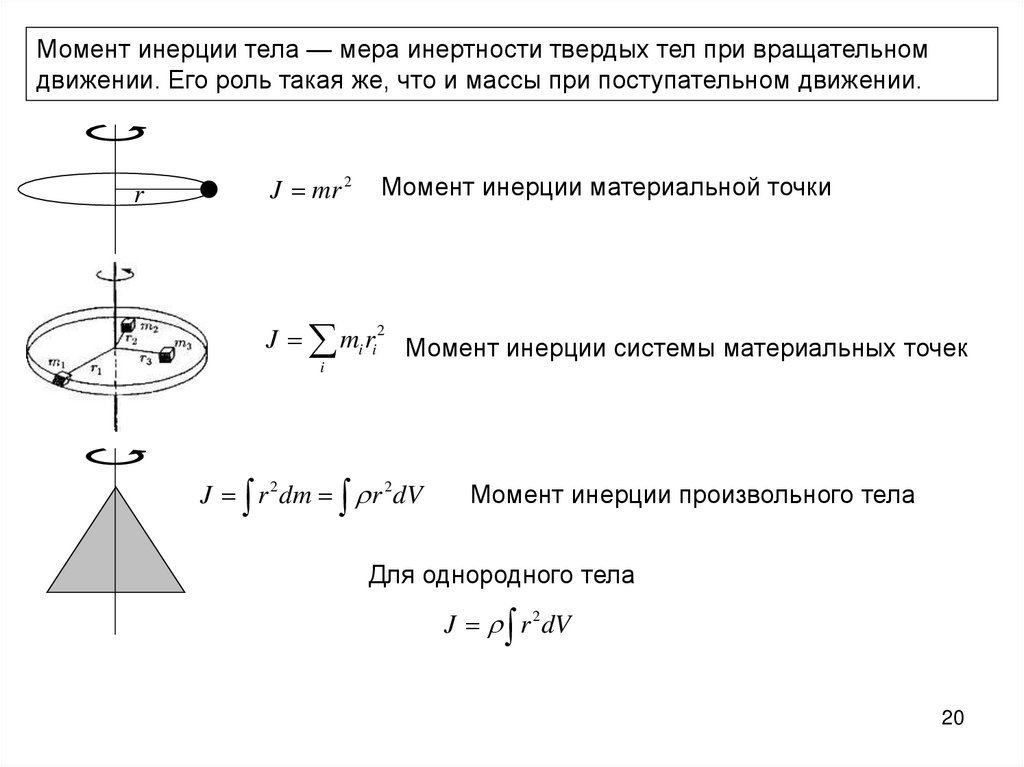
Момент инерции тела — мера инертности твердых тел при вращательном
движении. Его роль такая же, что и массы при поступательном движении.
r
J mr 2
Момент инерции материальной точки
J mi ri 2 Момент инерции системы материальных точек
i
J r 2 dm r 2 dV
Момент инерции произвольного тела
Для однородного тела
J r 2 dV
20

21.

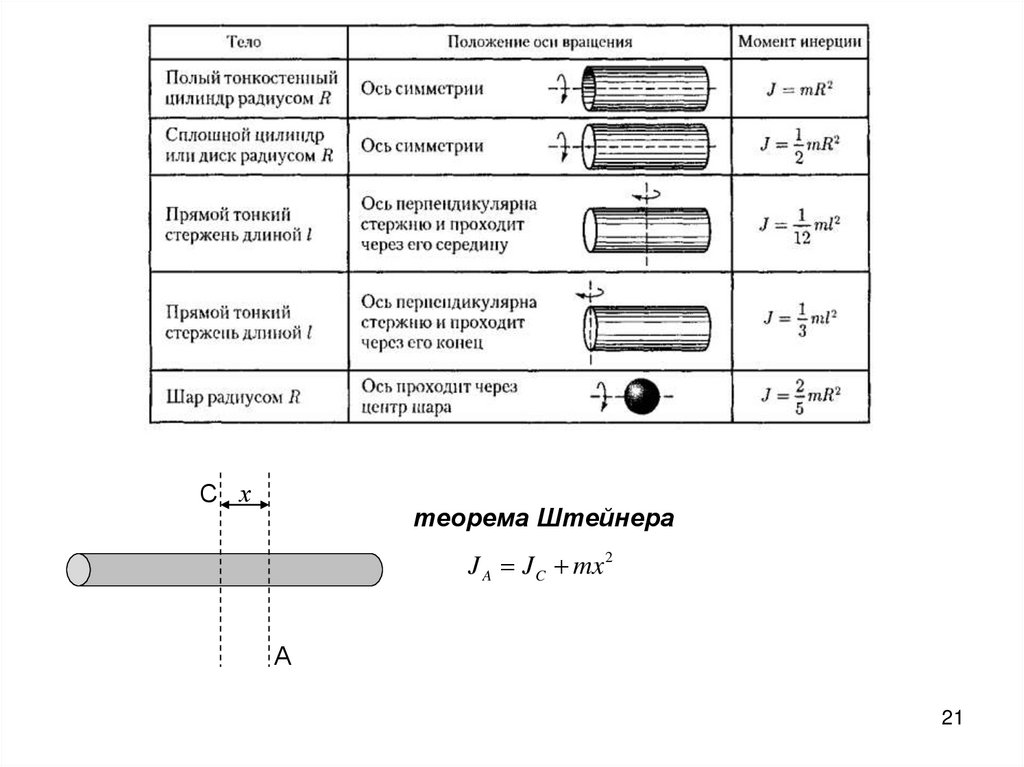
С х
теорема Штейнера
J A J C mx 2
А
21

22.

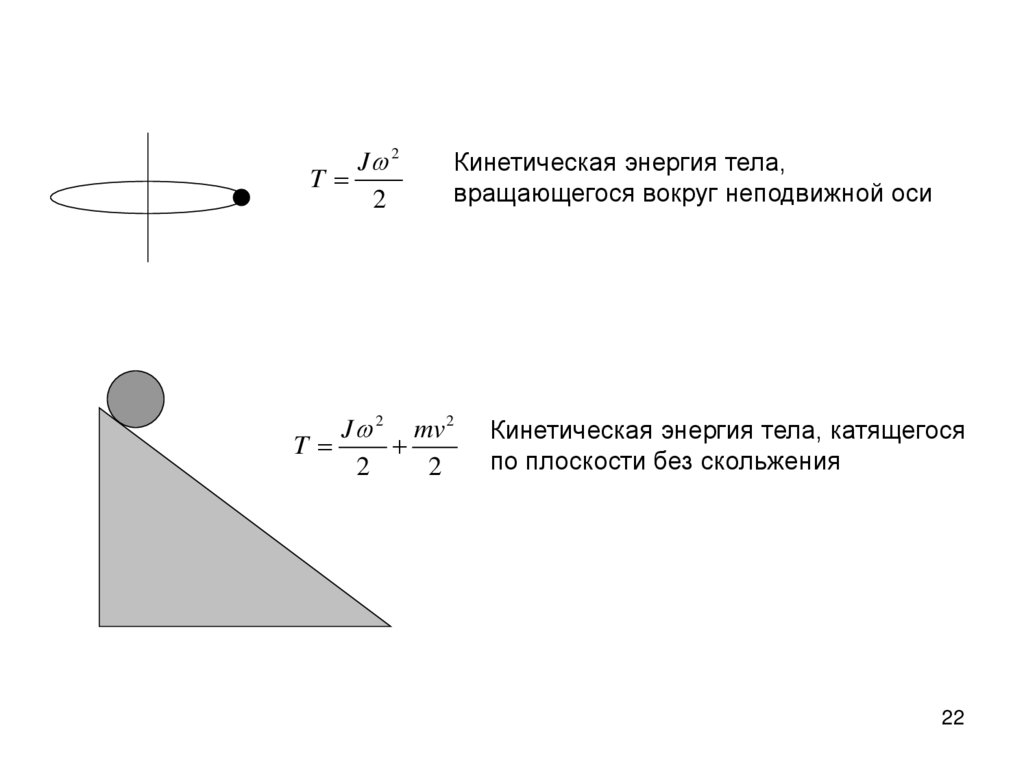
J 2
T
2
Кинетическая энергия тела,
вращающегося вокруг неподвижной оси
J 2 mv 2
T
2
2
Кинетическая энергия тела, катящегося
по плоскости без скольжения
22

23.

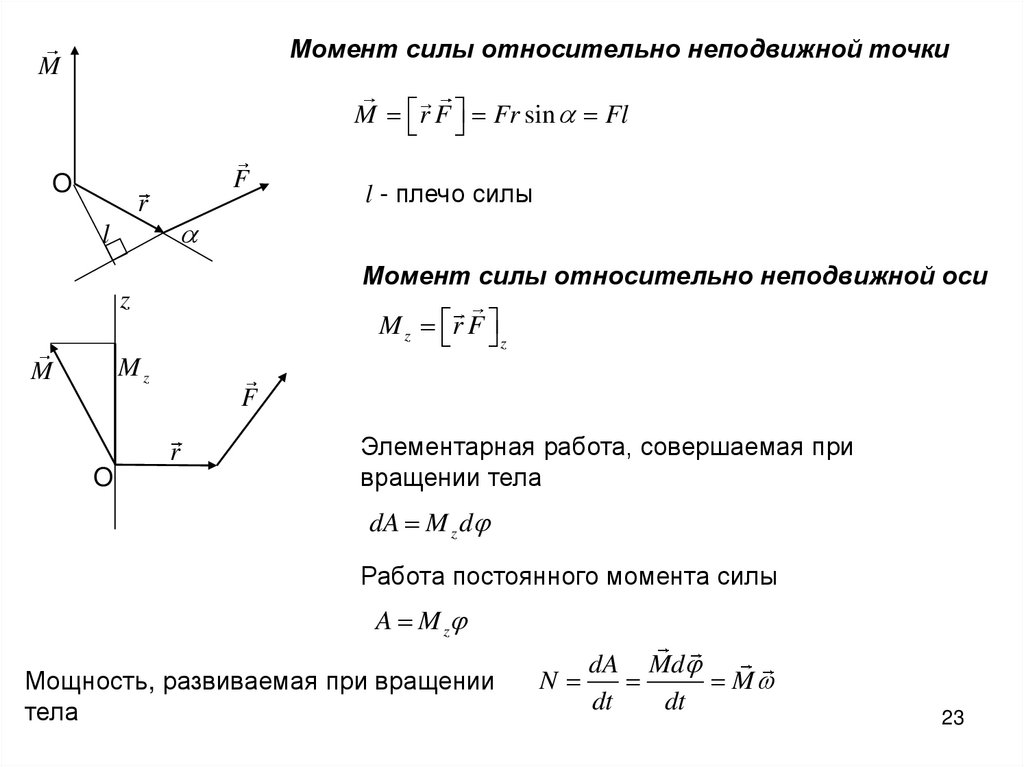
Момент силы относительно неподвижной точки
M
M r F Fr sin Fl
F
O
r
l
l - плечо силы
Момент силы относительно неподвижной оси
z
M z r F
z
Mz
M
F
r
O
Элементарная работа, совершаемая при
вращении тела
dA M z d
Работа постоянного момента силы
A M z
Мощность, развиваемая при вращении
тела
N
dA Md
M
dt
dt
23

24.

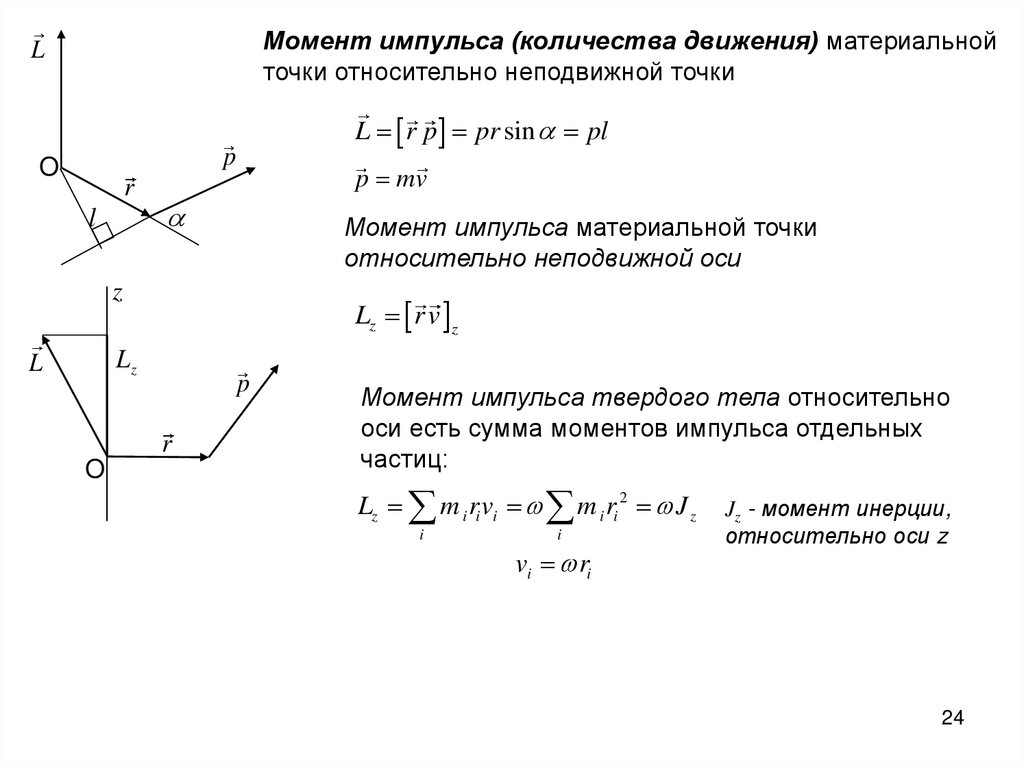
Момент импульса (количества движения) материальной
точки относительно неподвижной точки
L
L r p pr sin pl
p
O
r
l
p mv
Момент импульса материальной точки
относительно неподвижной оси
z
Lz r v z
Lz
L
p
r
O
Момент импульса твердого тела относительно
оси есть сумма моментов импульса отдельных
частиц:
2
Lz m i rv
i i m i ri J z
i
i
vi ri
Jz - момент инерции,
относительно оси z
24

25.

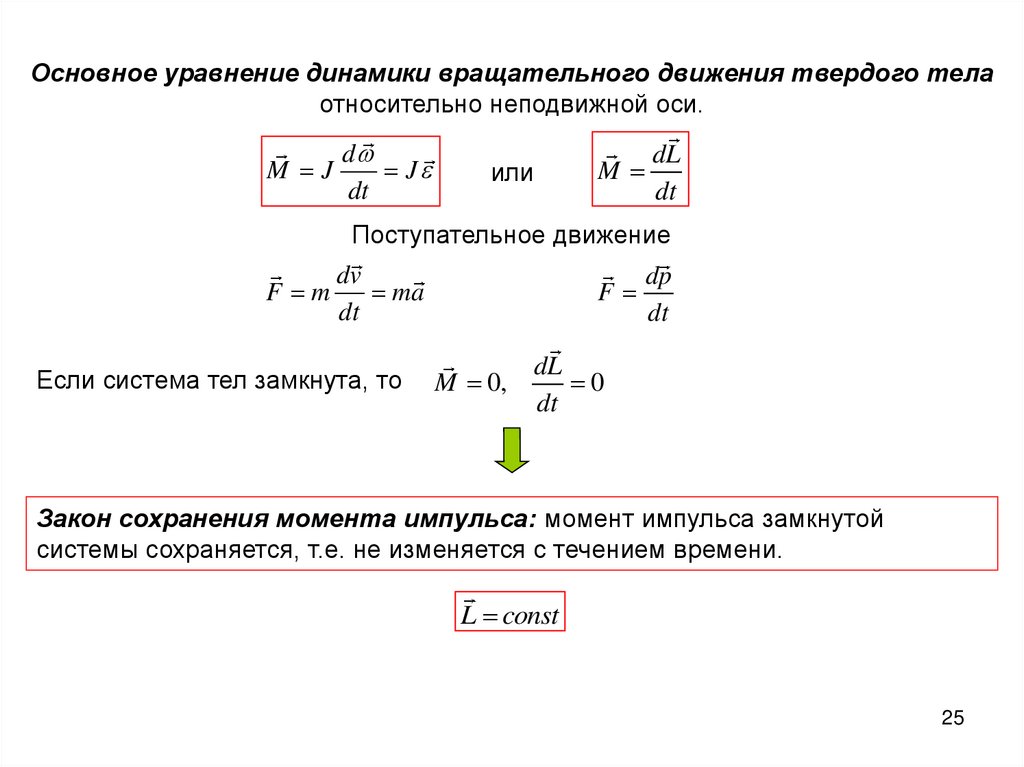
Основное уравнение динамики вращательного движения твердого тела
относительно неподвижной оси.
M J
d
J
dt
или
M
dL
dt
Поступательное движение
F m
dv
ma
dt
Если система тел замкнута, то
F
M 0,
dp
dt
dL
0
dt
Закон сохранения момента импульса: момент импульса замкнутой
системы сохраняется, т.е. не изменяется с течением времени.
L const
25

26.

Сопоставим основные величины и уравнения, определяющие вращение
тела вокруг неподвижной оси и его поступательное движение
26

27.

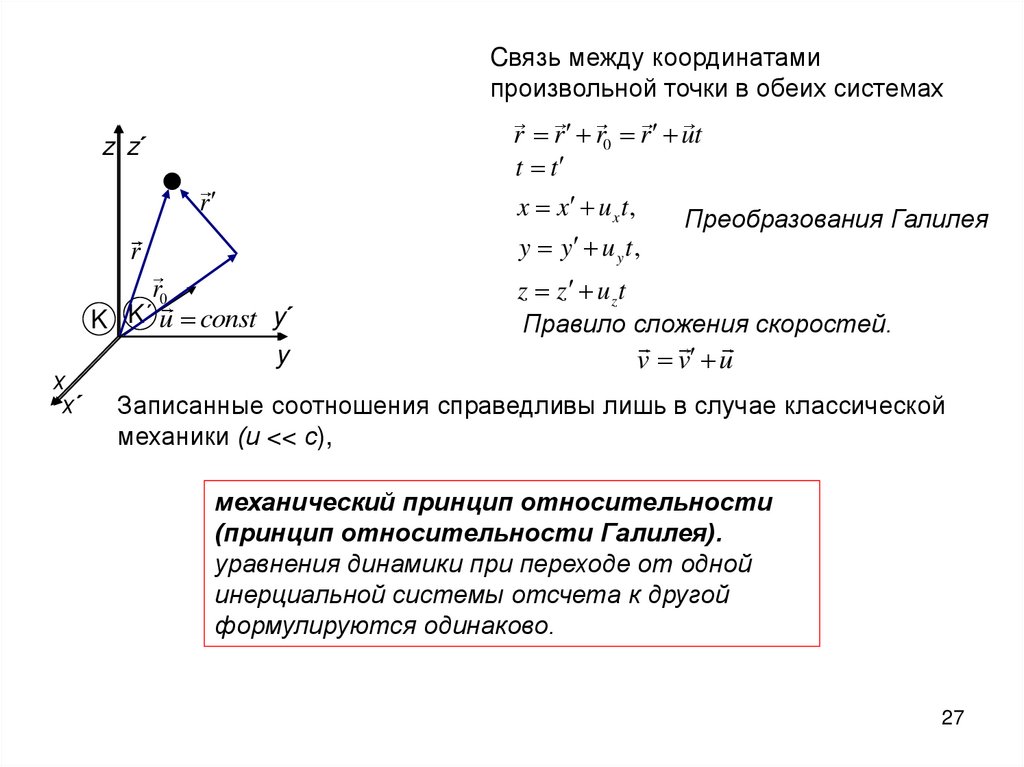
Cвязь между координатами
произвольной точки в обеих системах
z z´
r
r
х
х´
r0
K K´ u const y´
y
r r r0 r ut
t t
x x u x t ,
Преобразования Галилея
y y u y t ,
z z uzt
Правило сложения скоростей.
v v u
Записанные соотношения справедливы лишь в случае классической
механики (и << с),
механический принцип относительности
(принцип относительности Галилея).
уравнения динамики при переходе от одной
инерциальной системы отсчета к другой
формулируются одинаково.
27

28.

В основе специальной теории относительности лежат
постулаты Эйнштейна
I.
Принцип
относительности:
никакие
опыты
(механические,
электрические, оптические), проведенные внутри данной инерциальной
системы отсчета, не дают возможности обнаружить, покоится ли эта система
или движется равномерно и прямолинейно; все законы природы инвариантны
по отношению к переходу от одной инерциальной системы отсчета к другой.
II. Принцип инвариантности скорости света: скорость света в вакууме
не зависит от скорости движения источника света или наблюдателя и
одинакова во всех инерциальных системах отсчета
Преобразования Галилея
(и << с)
Преобразования Лоренца
(и ≈ с)
K K
t t
x x vt ,
y y ,
z z
K K
t
v
x
2
x vt
c
, x
,
2
2
v
v
1 2
1 2
c
c
y y , z z
t
28

29.

Длительность событий в разных системах отсчета
t
t
1
2
v
c2
- Релятивистское замедление хода часов,
Δt – промежуток времени в системе К,
относительно которой точка покоится
Длина тел в разных системах отсчета.
v2
l l0 1 2
c
- Релятивистское сокращение длины стержня,
l0 – длина стержня в системе К´, относительно которой
стержень покоится
Релятивистский закон сложения скоростей
v u
v
v u
1 2
c
v – скорость тела в системе К,
v´ – скорость тела в системе К´,
u – скорость системы К´ относительно системы К
29

30.

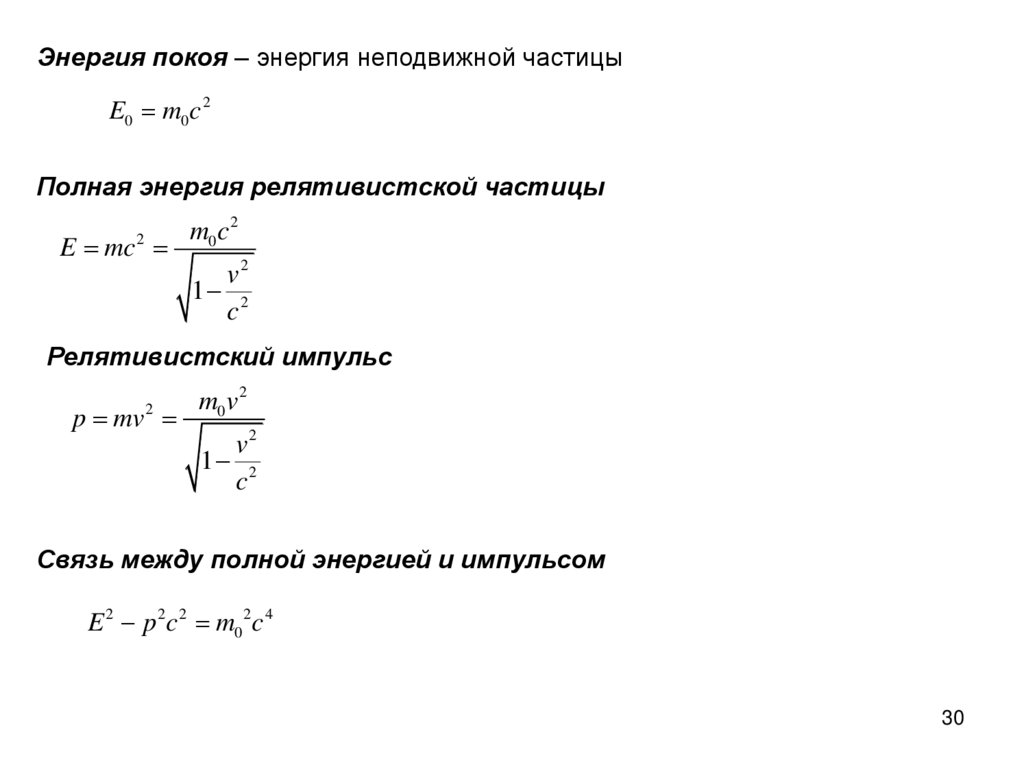
Энергия покоя – энергия неподвижной частицы
E0 m0 c 2
Полная энергия релятивистской частицы
E mc
2
m0 c 2
v2
1 2
c
Релятивистский импульс
p mv
2
m0v 2
v2
1 2
c
Связь между полной энергией и импульсом
E 2 p 2 c 2 m0 2c 4
30