Релятивистская кинематика. Основные представления классической физики

1.

Релятивистская кинематика
Основные представления классической физики
1. Принцип евклидового пространства.
Физическое пространство является 3-мерным евклидовым пространством.
2. Принцип абсолютного времени.
Время идет одинаково для всех тел.
3. Принцип инерции.
Свободное тело движется прямолинейно и равномерно относительно других
свободных тел (инерциальных систем).
4. Принцип относительности Галилея.
Все механические явления в инерциальных системах отсчета протекают
одинаково.
5. Принцип сохранения импульса.
В замкнутой системе сохраняется количество движения (импульс).

2.

Релятивистская кинематика
Основные представления классической физики
Следствия:
1. Преобразования Галилея
r r Vt
t t
r r Vt
t t
2. Правило сложения скоростей
v v V
3. Инвариантность длины и промежутков времени
l l , t t
4. Импульс
p mv
5. Сохранение массы.
Сохранение кинетической энергии в упругих столкновениях.

3.

Релятивистская кинематика
Постулаты Эйнштейна
D
D
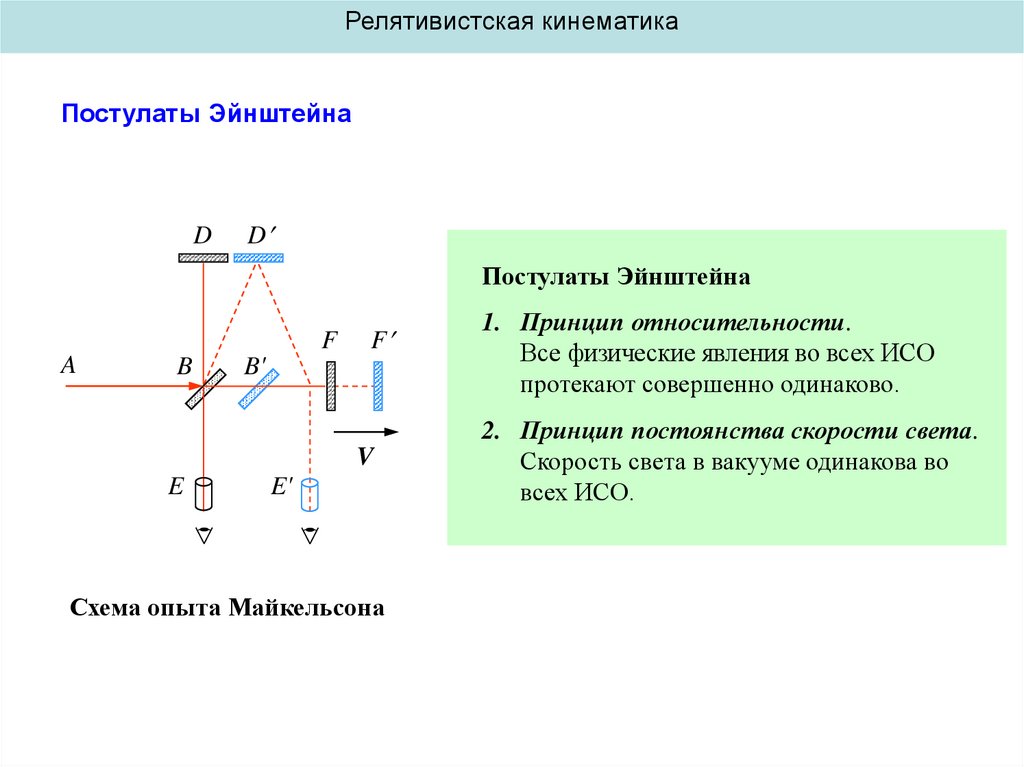
Постулаты Эйнштейна
F
A
B
F
B'
V
E
E'
Схема опыта Майкельсона
1. Принцип относительности.
Все физические явления во всех ИСО
протекают совершенно одинаково.
2. Принцип постоянства скорости света.
Скорость света в вакууме одинакова во
всех ИСО.

4.

Релятивистская кинематика
Основные представления СТО
1. Принцип евклидового пространства.
Физическое пространство является 3-мерным евклидовым пространством.
2. Принцип абсолютного времени постоянства скорости света.
Скорость света в вакууме одинакова во всех ИСО.
3. Принцип инерции.
Свободное тело движется прямолинейно и равномерно относительно других
свободных тел (инерциальных систем).
4. Принцип относительности Галилея СТО (Эйнштейна).
Все физические явления в инерциальных системах отсчета протекают
одинаково.
5. Принцип сохранения импульса.
В замкнутой системе сохраняется количество движения (импульс).

5.

Релятивистская кинематика
Синхронизация часов
t0 r c
r
t0
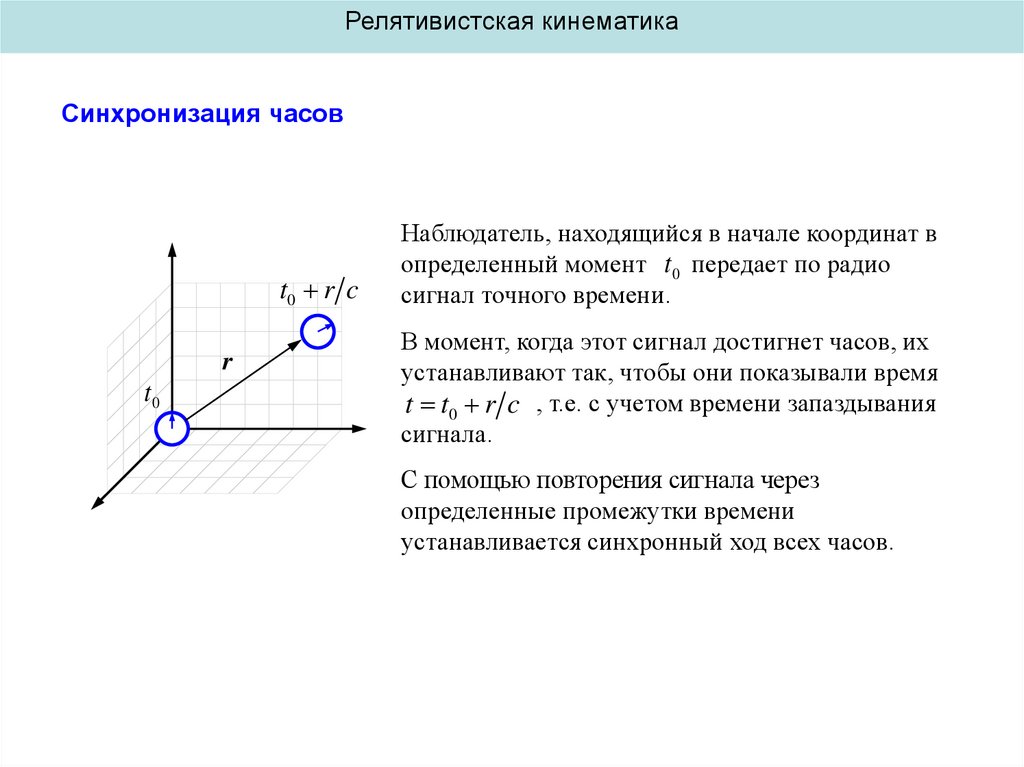
Наблюдатель, находящийся в начале координат в
определенный момент t 0 передает по радио
сигнал точного времени.
В момент, когда этот сигнал достигнет часов, их
устанавливают так, чтобы они показывали время
t t0 r c , т.е. с учетом времени запаздывания
сигнала.
С помощью повторения сигнала через
определенные промежутки времени
устанавливается синхронный ход всех часов.

6.

Релятивистская кинематика
Соотношения между событиями
A
K'
B
V
A, B фотоэлементы
K
Система K':
t A
l
l
, tB
2c
2c
Система K:
tA
l
l
, tB
2(c V )
2(c V )
t A tB
t A tB
События, одновременные в одной системе отсчета, не являются
одновременными в другой системе отсчета.
Одновременность является относительной.
Время в разных системах отсчета течет по разному.

7.

Релятивистская кинематика
Замедление времени и сокращение длины
Построение ИСО
ИСО система координат + система синхронизированных часов
неподвижный атом
, T естественные эталоны длины и времени
1 м = k
практические эталоны
1 c = mT
1960 1983: 1 метр равен 1 650 763,73 длин волн оранжевой линии (6056 Å)
спектра излучения изотопа криптона 86Kr в вакууме.
Современное определение: 1 метр равен длине пути, проходимого светом в
вакууме за (1 / 299 792 458) секунды.
Современное определение: 1 секунда равна 9 192 631 770 периодам излучения,
соответствующего переходу между двумя сверхтонкими уровнями основного
состояния атома 133Cs .

8.

Релятивистская кинематика
Замедление времени и сокращение длины
K'
K
OA = 1 м (в системе K)
?
A'
O'A' = 1 м (в системе K')
A
A' > или < A ?
Пусть l уменьшается при движении.
V
O'
С точки зрения K'
O
x, x'
A < A'
С точки зрения K A' < A
противоречие
A = A' (совпадение)
Таким образом, имеет место равенство поперечных размеров тел или
y y,
z z

9.

Релятивистская кинематика
Замедление времени и сокращение длины
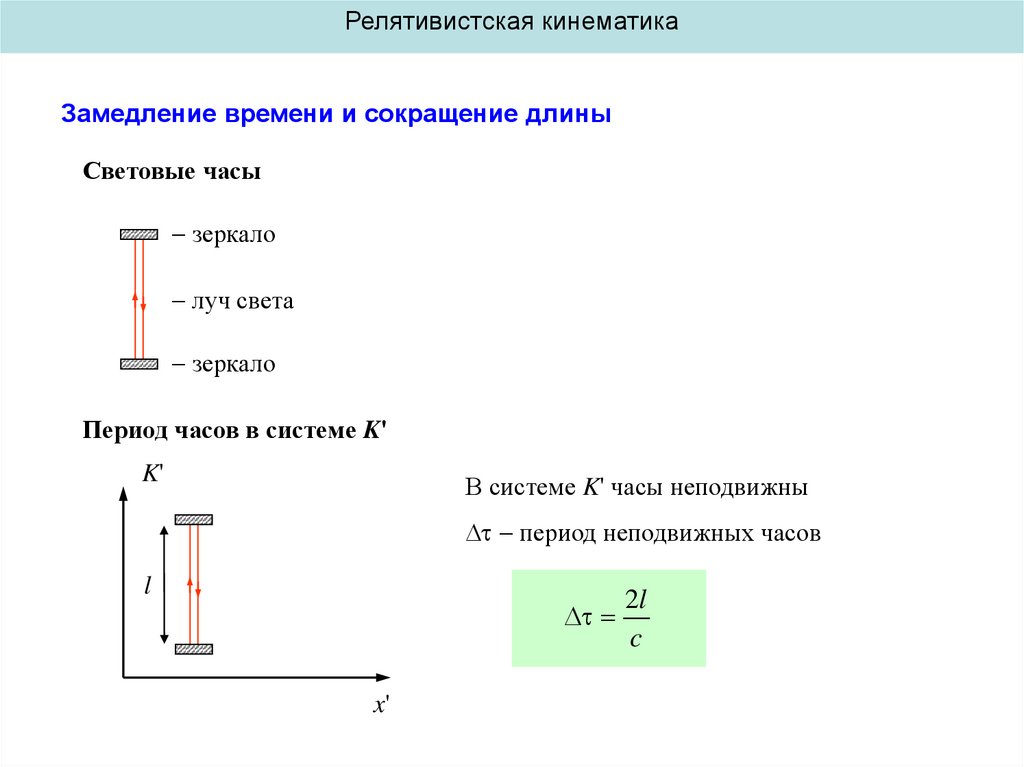
Световые часы
зеркало
луч света
зеркало
Период часов в системе K'
K'
В системе K' часы неподвижны
период неподвижных часов
l
x'
2l
c

10.

Релятивистская кинематика
Замедление времени и сокращение длины
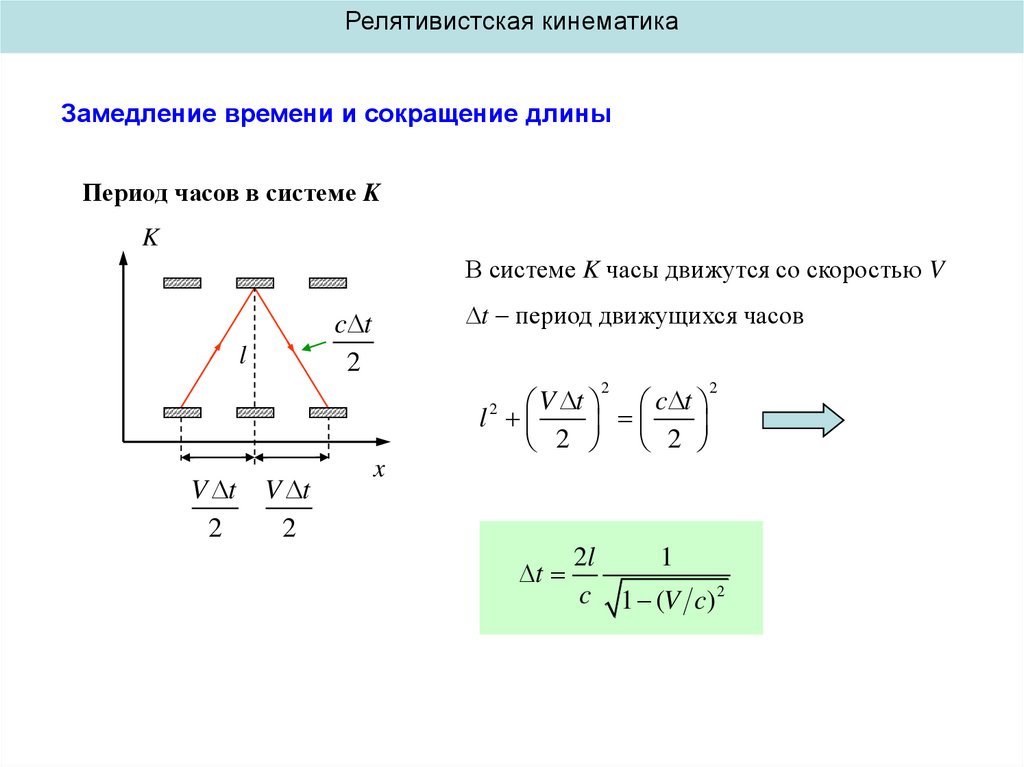
Период часов в системе K
K
В системе K часы движутся со скоростью V
t период движущихся часов
c t
2
l
V t c t
l
2 2
2
2
2
V t
2
V t
2
x
t
2l
1
c 1 (V c ) 2

11.

Релятивистская кинематика
Замедление времени и сокращение длины
t
Лоренц фактор системы
1
1 2
,
V
c
собственное время (время часов, связанных с телом)
t
замедление времени
Движущиеся часы идут медленнее, чем покоящиеся.
Экспериментальное подтверждение:
Мюоны , собственное время жизни = 2 10–6 с.
Время жизни быстрых мюонов (в космических лучах) >
и соответствует формуле замедления времени.

12.

Релятивистская кинематика
Замедление времени и сокращение длины
Парадокс часов (близнецов)
V
B
A
С точки зрения A tA > tB
С точки зрения B tB > tA
2l A
V
2l
tB B
V
tA
t A tB
? парадокс
lB
lA
часы B отстанут от A (близнец A окажется старше B)

13.

Релятивистская кинематика
Замедление времени и сокращение длины
Лоренцево сокращение
K
K': l0 собственная длина
K'
K: l длина движущегося стержня
l0
A
B
M
l V
l0 V t
l l0
время пролета стержня l мимо M
t время пролета метки M длины l0
t
l
l0
l0 1 V 2 c 2
сокращение длины
Продольный размер движущегося стержня меньше его собственной длины.

14.

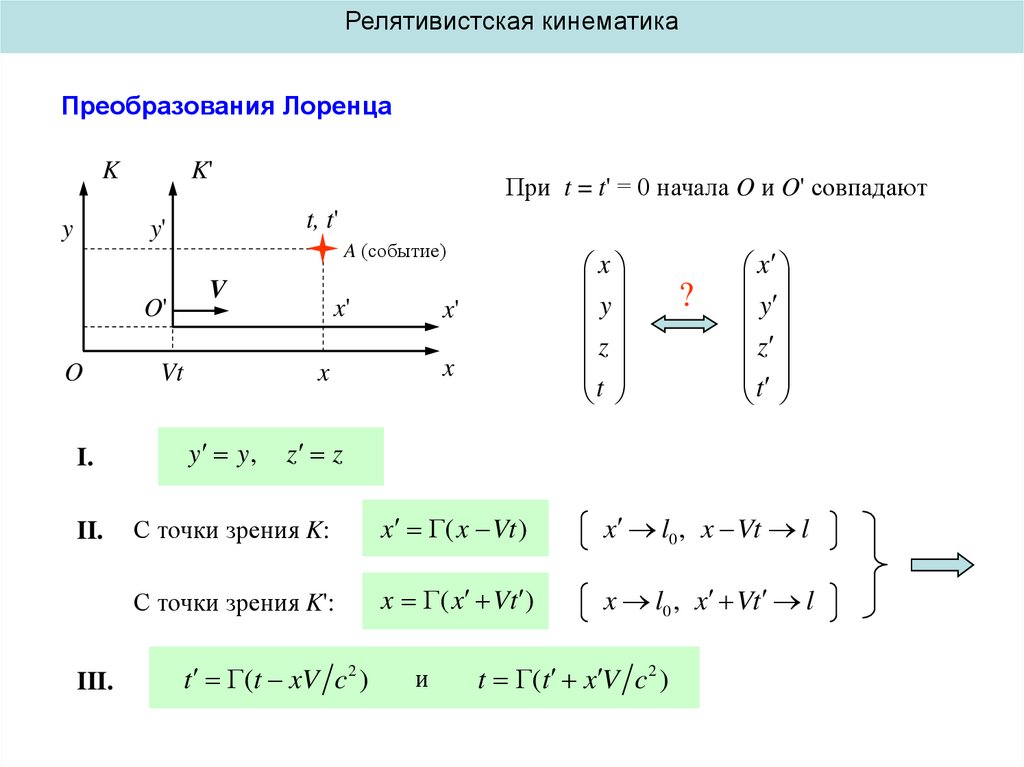
Релятивистская кинематика
Преобразования Лоренца
K
y
K'
t, t'
y'
O'
O
I.
II.
III.
При t = t' = 0 начала O и O' совпадают
A (событие)
V
Vt
x'
x'
x
x
y y,
x
y
z
t
?
x
y
z
t
z z
С точки зрения K:
x ( x Vt )
x l0 , x Vt l
С точки зрения K':
x ( x Vt )
x l0 , x Vt l
t (t xV c 2 )
и
t (t x V c 2 )

15.

Релятивистская кинематика
Преобразования Лоренца
x ( x Vt )
y y
x ( x Vt )
y y
z z
z z
t (t xV c 2 )
t (t x V c 2 )
1 1 2 ,
При
V
c, x c
Преобразования Лоренца
V c
t
Преобразования Галилея

16.

Четырехмерный мир (пространство Минковского)
Интервал
s интервал (между событиями)
Определение:
s 2 c 2 t 2 r 2
Из преобразований Лоренца
или
c 2 t 2 r 2 c 2 t 2 r 2
s 2 c 2 t 2 r 2 inv
Типы интервалов
1.
r c t
пространственноподобный ( K', в которой t' = 0 )
2.
r c t
времениподобный ( K', в которой r' = 0 )
3.
r c t
светоподобный

17.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Определение 1:
R (ct, x, y, z )
четырехвектор события (мировой точки)
R 2 c 2t 2 x 2 y 2 z 2
квадрат длины
Компоненты R преобразуются в соответствии с преобразованиями Лоренца
Определение 2:
Четырехскаляром (инвариантом) называется величина, не зависящая от
выбора ИСО a a
R2
четырехскаляр

18.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Определение 3:
A ( At , Ax , Ay , Az ) четырехвектор
Компоненты A преобразуются в соответствии с преобразованиями Лоренца
Ax ( Ax At )
A y Ay
Ax ( Ax At )
Ay A y
Az Az
At ( At Ax )
Az Az
1 1 2 ,
At ( At Ax )
V c

19.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Свойства четырехвекторов
A2 At2 Ax2 Ay2 Az2
1.
A2 inv
2.
A B
квадрат длины четырехвектора
четырехскаляр
A B
Равенство четырехвекторов сохраняется во всех ИСО
Четырехвектора можно складывать и умножать на числа как и обычные векторы.
Типы четырехвекторов
1.
A2 0
пространственноподобный
2.
A2 0
времениподобный
3.
A2 0
светоподобный

20.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Четырехскорость
V
dR
d
, собственное время материальной точки
dt d
V
1
dR
( c, v x , v y , vz )
dt
1 2 , v c
или
V ( c, v)
V 2 2c2 2v2 2c2 (1 v2 c2 ) c 2

21.

Четырехмерный мир (пространство Минковского)
Пространство Минковского
Релятивистский закон сложения скоростей
Из преобразований Лоренца для четырехскорости
v x
vx V
,
1 vx c
v y
При малых скоростях
v x v x V ,
v y v y ,
V
vy
(1 vx c)
c, v
v z vz
,
v z
vz
(1 vx c)
c
или
v v V
Релятивистский закон сложения скоростей соответствуют второму
постулату Эйнштейна о неизменности скорости света c во всех ИСО.

22.

Релятивистская динамика
Нерелятивистский импульс
Если в результате столкновения шаров (тел) движение одного шара
"уменьшилось", то движение другого шара "увеличилось".
Поэтому предполагается, что при соударении тел сумма мер движения
шаров не меняется.
Закон сохранения импульса (для замкнутых систем)
p
i
const,
pi mi vi
Следствия:
1. Закон сохранения массы.
2. Закон сохранение кинетической энергии при абсолютно упругих
столкновениях

23.

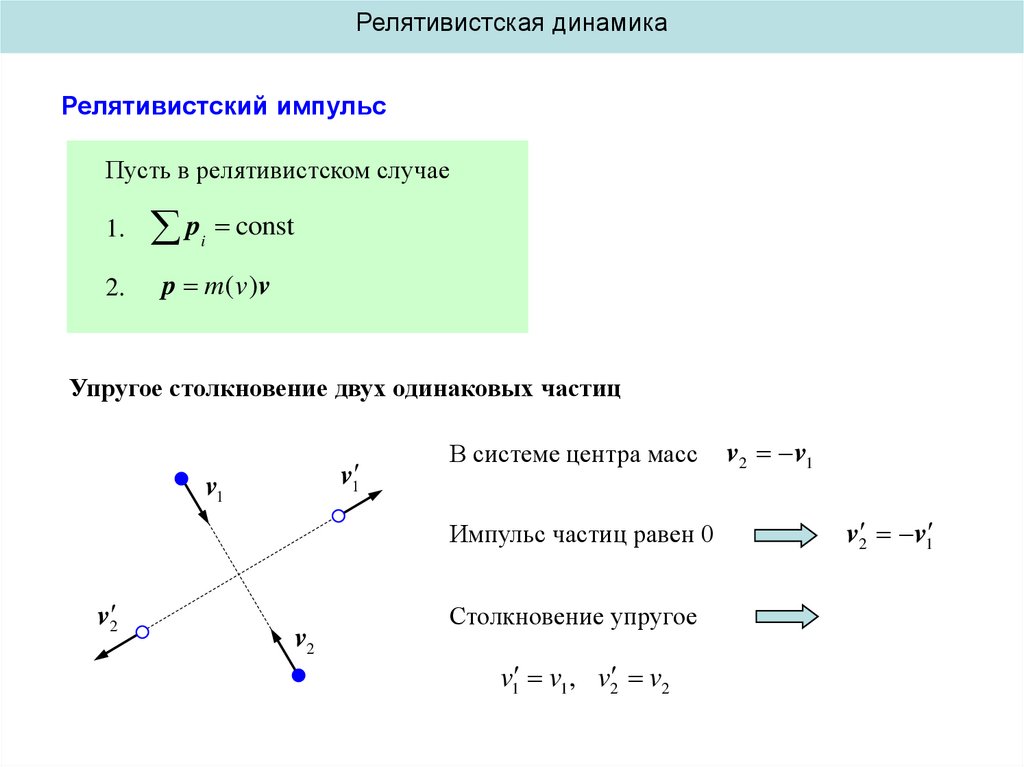
Релятивистская динамика
Релятивистский импульс
Пусть в релятивистском случае
1.
2.
p
i
const
p m( v )v
Упругое столкновение двух одинаковых частиц
v1
v1
В системе центра масс
Импульс частиц равен 0
v2
v2
Столкновение упругое
v1 v1 , v2 v2
v2 v1
v2 v1

24.

Релятивистская динамика
Релятивистский импульс
4-импульс
P mV ( mc, mv)
m обычная масса
при
v 0
mv mv
В системе центра масс
P1 P2 P1 P2
4-вектор
(2 mc,0,0,0) (2 mc,0,0,0)
4-вектор
данное равенство сохраняется во всех ИСО

25.

Релятивистская динамика
Релятивистский импульс
P1 P2 P1 P2
или
( 1mc 2mc, 1mv1 2mv2 ) ( 1 mc 2mc, 1 mv1 2mv2 )
p1 p2 const
p mv
релятивистский импульс
Данное выражение импульса единственное совместимое с
принципом сохранения импульса при столкновении двух частиц
p
i
const, p mv
закон сохранения импульса

26.

Релятивистская динамика
Релятивистский энергия
Определение:
E mc 2
релятивистский энергия
4-импульс системы
Ei
,
m
v
i i i
c
Так как в замкнутой системе во всех ИСО сохраняются
пространственные компоненты 4-импульса системы
Сохраняется также временная компонента 4-импульса системы, или
E
i
const, E mc2
закон сохранения энергии

27.

Релятивистская динамика
Релятивистский энергия
При малых скоростях
E0 mc 2
2
mv
E mc 2 mc 2
2
энергия покоя
K E E0 ( 1)mc 2
кинетическая энергия
При упругих столкновениях
K
i
const
Таким образом, закон сохранения импульса приводит к
закону сохранения энергии и к
закону сохранения кинетической энергии (для упругих столкновений)

28.

Релятивистская динамика
Релятивистский энергия
4-вектор энергии-импульса (4-импульса)
E
P ,
c
p
P 2 E 2 c 2 p 2 m2c 2
Энергия и импульс света
При v = c
pc 2
E
v
E pc
E 2 c 2 p 2 m 2c 2 0
m 0
Данные соотношения подтверждаются экспериментально,
например, при изучении эффекта Комптона.

29.

Релятивистская динамика
Релятивистская сила
E c p m c
dE
dp
v
dt
dt
L r p
dL
dp
r
dt
dt
2
d
dt
2
2
2 2
Исходя их этого, сила (как мера воздействия) определяется как
F
dp
dt
4-вектор силы
F
dP
d
dt d
dE
vF
dt

30.

Релятивистская динамика
Релятивистская сила
F ( Fv ), F
c
В соответствии с преобразованиями Лоренца
B
( Fv )
c
Fx
,
1 v x c
Fx
F v
Fv VFx
,
1 v x c
Fy
Fy
(1 v x c )
,
Fz
Fz
(1 v x c )