Similar presentations:
Специальная теория относительности. Лекция 6
1. Специальная теория относительности
Лекция №62. План лекции
• 1. Принцип относительности Галилея.• 2. Постулаты СТО.
• 3. Преобразования Лоренца. Следствия из
преобразований Лоренца.
• 4. Интервал.
• 5. Релятивистская динамика.
• 6. Закон взаимосвязи массы и энергии.
• 7. Границы применимости классической
механики.
3. 1. Принцип относительности Галилея
Принцип относительностиГалилея:
Все законы механики
одинаковы во всех ИСО.
Галилео
Галилей
(1564 -1642)
итальянский философ,
математик, физик,
механик и астроном
4.
Преобразования Галилея позволяютсделать
переход из одной ИСО в другую. В его основе лежат
две аксиомы:
аксиома 1 – ход времени одинаков во всех системах
отсчета.
аксиома 2 – расстояния между двумя точками, а
также размеры тела в любой системе отсчета (СО)
не зависят от скорости ее движения.
5.
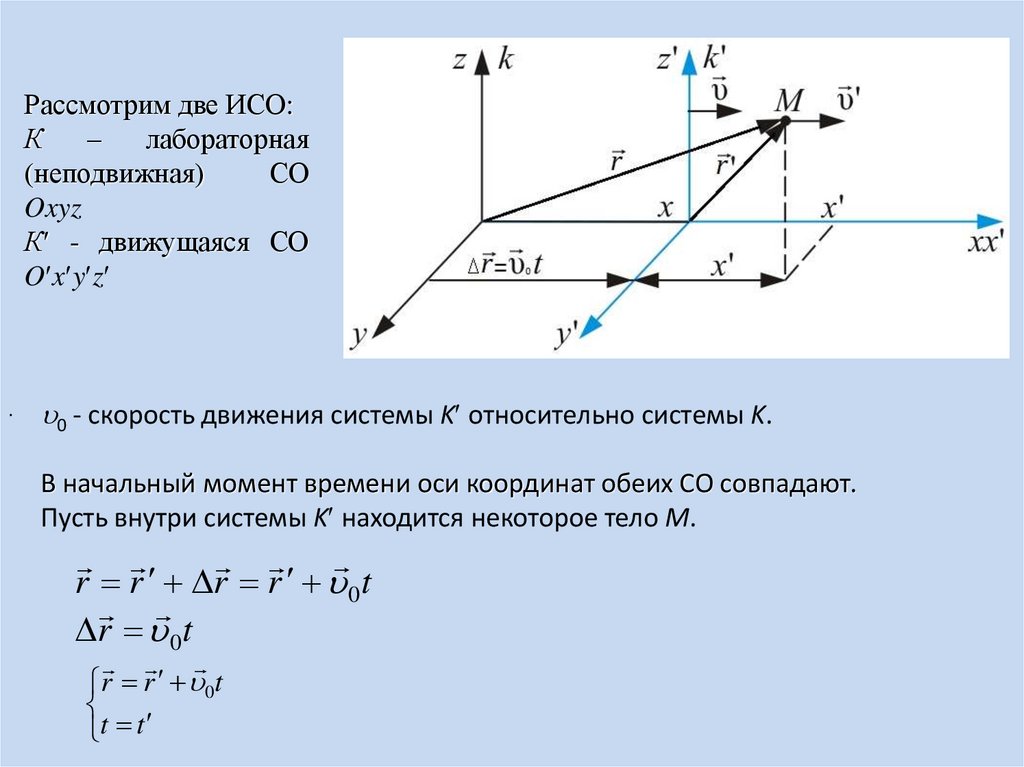
Рассмотрим две ИСО:К
–
лабораторная
(неподвижная)
СО
Oxyz
К - движущаяся СО
O x y z
.
0 - скорость движения системы K относительно системы K.
В начальный момент времени оси координат обеих СО совпадают.
Пусть внутри системы K находится некоторое тело M.
r r r r 0t
r 0 t
r r 0t
t t
6.
Спроектируем на координатные оси:x x 0 t
y y
z z
t t
(1)
или
x x 0t
y y
z z
t t
(2)
Системы уравнений (1) и (2) называются
преобразованиями Галилея.
Используя уравнения (1) и (2), можно перейти от описания
движения тела в одной системе отсчета к другой системе
отсчета.
Из преобразований Галилея вытекает теорема (закон)
сложения скоростей.
7.
Продифференцируемdr dr
0
dt dt
0
r r 0t по времени:
( 0 = const)
теорема о сложении скоростей в классической
механике
- скорость движения точки в неподвижной ИСО К; - скорость движения
точки в движущейся ИСО K ; 0 - скорость движения системы K
относительно системы K.
В теоретической механике эту теорему записывают в виде
абс отн пер
Продифференцируем полученное выражение по времени еще
раз:
d d d 0 d
или
a a
dt
dt
dt
dt
F F
F ma, значит
8. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ
Величины, не изменяющиеся при переходе от однойсистемы отсчета к другой, т. е. не зависящие от
преобразований
координат,
называются
инвариантными величинами или инвариантами
преобразований.
1) ускорение
2) силы
3) масса
4) длина тела и т.д.
9.
• Принцип относительности Галилея: законы механикиодинаковы во всех инерциальных системах отсчета.
• Это значит, что в разных ИСО все механические процессы
при одних и тех же условиях протекают одинаково.
• Инвариантными по отношению к преобразованиям Галилея, при
переходе от одной ИСО к другой, оказываются также уравнения, вид
которых не изменяется при таком переходе. Величины, входящие в эти
уравнения, могут при переходе от одной СО к другой изменяться, однако
формулы, выражающие связь между этими величинами, остаются
неизменными.
p m
E k A
• принцип относительности Галилея: уравнения механики
инвариантны по отношению к преобразованиям Галилея.
10. 2. Постулаты СТО
11.
1-ый постулат СТО (принцип относительности Эйнштейна)является
обобщением
классического
принципа
относительности с механических на любые физические
явления.
Первая формулировка. Никакими физическими опытами
(механическими, электрическими, оптическими) проведенными
в ИСО, нельзя доказать покоится эта система или движется
равномерно и прямолинейно относительно другой ИСО.
Вторая
формулировка.
Все
процессы
в
природе
(механические, электрические, оптические) во всех ИСО
протекают одинаково.
Эйнштейн показал, что преобразования Галилея должны быть
заменены более общими преобразованиями Лоренца.
Третья формулировка. уравнения выражающие законы
природы, инвариантны по отношению к преобразованиям
Лоренца.
12.
2-ой постулат СТО (принцип инвариантности скоростисвета). Скорость света в вакууме не зависит от скоростей
движения источника и приемника света, и является
максимально возможной скоростью движения в природе.
c = 3,00·108 м/с
Из второго постулата следует, что скорость света в вакууме является
величиной инвариантной, т. е. она одинакова для всех направлений и во
всех ИСО.
Скорость света является одной из важных физических постоянных и она
в вакууме является предельной.
Опыты показали, что скорость любых тел и частиц, а также скорость
распространения любых сигналов и взаимодействий не может
превосходить скорости света.
Механика, описывающая движения с околосветовыми
скоростями, называется релятивистской механикой.
13.
Из 2-го постулата следует, что время в различных системах отсчета течет поразному.
Существование предельной скорости приводит к тому, что пространство и
время утрачивают приписывавшуюся им обособленность, т.е. независимость
друг от друга.
Когда начала систем К и К совпадали из общего начала излучена световая
волна. Фронт волны за время t прошел расстояние х в системе К, а в системе
К расстояние х за время t
x ct
x' ct '
т. к.
x x'
то
t t'
Вывод:
Время в различных системах отсчета течет неодинаково, т. е.
не является универсальным.
14.
• В СТО пространство и время взаимосвязаны, образуяединое четырехмерное пространство-время.
• «Точечное» событие характеризуется четырьмя величинами –
координатами x, y и z, указывающими, где оно произошло, и временем t
– когда оно произошло.
• Значения этих четырех величин зависят от СО, в которой «наблюдаем»
это событие.
• В четырехмерном пространстве (пространство–время) возьмем
прямоугольную систему координат с осями x, y, z и ct. Тогда событие
можно изобразить точкой, которую называют мировой точкой.
• С течением времени мировая точка изменяет свое положение в
четырехмерном пространстве, описывая траекторию, которая называется
мировой линией.
• Если частица неподвижна в обычном пространстве, ее мировая точка
перемещается параллельно оси ct.
• При переходе к другой ИСО значения координат x, y, z, а также времени t
изменяются и становятся равными x , y , z и t .
15. ПРОСТРАНСТВО
Классическая механикаРелятивистская механика
Евклидовое –
трехмерное
М (x, y, z)
Время однородно,
пространство однородно
и изотропно.
Время и пространство
отделены друг от друга.
Минковского –
четырехмерное
М (x, y, z, ct)
Время однородно,
пространство однородно
и изотропно.
Время и пространство
связаны друг с другом.
16.
17. 3. Преобразования Лоренца. Следствия из преобразований Лоренца.
• А)Относительность
одновременности
событий.
• Б) Длина тел в разных системах отсчета.
• В) Промежуток времени между событиями.
• Г)
Релятивистский
закон
сложения
скоростей.
18. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
В релятивистской механике преобразования координатГалилея заменяются на преобразования координат Лоренца.
x 0t
x
2
1 02
c
y y
z z
0 x
t 2
t
c
2
1 02
c
(3)
x 0 t
x
2
1 02
c
y y
z z
t 0 x
t
c2
2
1 02
c
(4)
19.
Иногда для упрощения записи вводятрелятивистский множитель
0
c
Если 0 << c ( << 1), то
преобразования Лоренца
переходят в преобразования
Галилея.
Из преобразований Лоренца
можно получить ряд следствий.
Хе́ндрик Анто́н
Ло́ренц
(1853 —1928)
нидерландский
физик.
20. А) ОТНОСИТЕЛЬНОСТЬ ОДНОВРЕМЕННОСТИ СОБЫТИЙ
Пусть в системе K в двух разных точках с координатами x1 и x2(x1 x2) в один и тот же момент времени (t1 = t2) происходят
два события.
t1
t1
0 x1
1
t 2 t1
c2
t 2
02
c
t2
0 x2
1
2
t 2 t1
c
2
0
2
1
c2
02
c2
x1 x2 x1 x2
c
2
0
2
c
2
0
2
1
c
2
0
2
0
События,
одновременные
в
системе
К,
в
системе
К
оказываются неодновременными,
т. е. одновременность событий –
относительна.
Вывод:
Время – неинвариантная величина
21. Б) РЕЛЯТИВИСТСКОЕ ИЗМЕНЕНИЕ ДЛИНЫ
Пусть в системе K покоитсястержень длиной l0 = x2 - x1
(собственная длина тела).
Длина стержня в системе K равна
l = x2 - x1 ,
где x1 и x2 – координаты концов стержня в системе K,
измеренные в один и тот же момент времени (t1 = t2).
22.
Используем прямые преобразования координат:x1 '
x1 t
1
c
2
x2 '
и
x 2 t
1
c
2
Тогда
l0 x2 x1
x2 x1 0t1 0t 2
1
02
c
2
x2 x1
1
02
c
2
l
1
02
c
2
23. РЕЛЯТИВИСТСКОЕ ИЗМЕНЕНИЕ ДЛИНЫ
l0l
1
c
2
Это и есть релятивистское
изменение длины -
l l0
1
c
Его также называют
лоренцевым сокращением длины
2
24. РЕЛЯТИВИСТСКОЕ ИЗМЕНЕНИЕ ДЛИНЫ
Размеры тела относительно неподвижной СОсокращаются только в направлении движения
относительно неподвижной системы отсчета.
а) тела неподвижные;
б) тела движутся со
скоростью
25. СЛЕДСТВИЯ
1 c, то 0 и l l0 – классическая физикаc
2 ~ c , то 1 и
c
2
1 1
c
, тогда l l0
Вывод:
Линейные размеры тела максимальны в той ИСО,
относительно которой тело покоится.
.
26. В) Промежуток времени между событиями (ДЛИТЕЛЬНОСТЬ СОБЫТИЙ)
Пусть в системе К в одной и той же точке (х2 =х1 =х ) происходитнекое событие длительностью = t2 - t1 .
- собственное время
Найдем длительность этого события в системе K:
t 2 t1
Используем обратные
преобразования времени:
27.
x't 2 ' 2
c
t2
2
1
c
t 2 t1
t 2
и
0 x1
c
2
t1
1
Получаем:
02
c
t1
c 2 t 2 t1
1
2
02
c
x'
c2
1
c
0 x2
2
2
1
02
c2
1
>
t1 '
02
c2
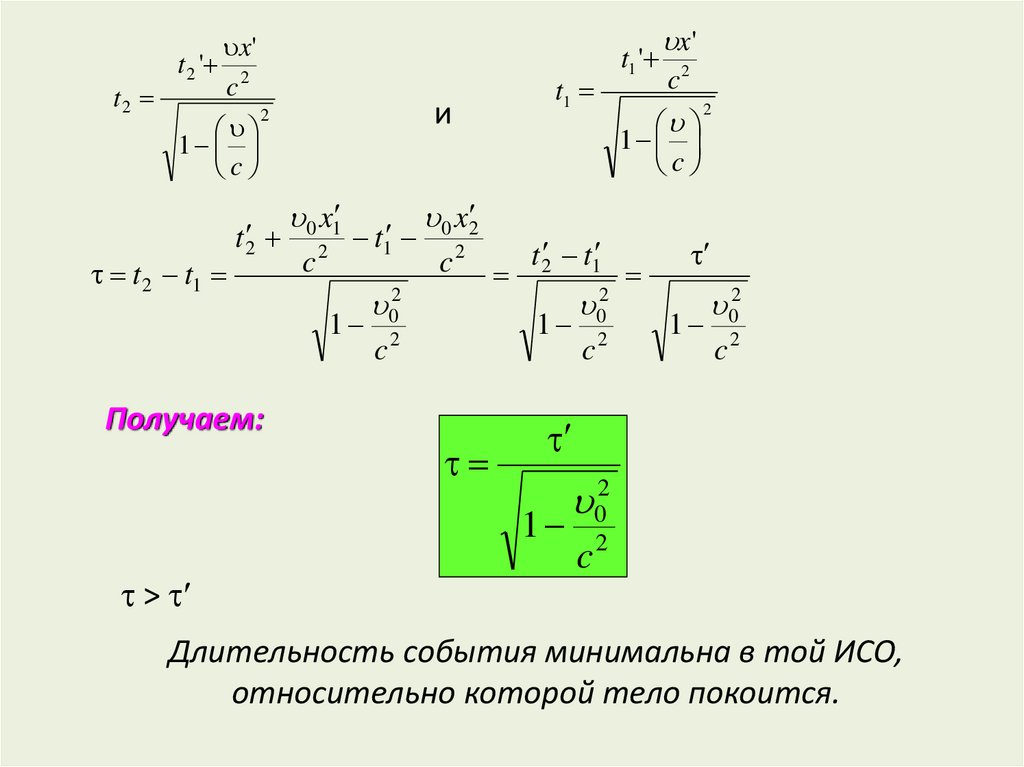
Длительность события минимальна в той ИСО,
относительно которой тело покоится.
28. РЕЛЯТИВИСТСКОЕ ИЗМЕНЕНИЕ ПРОМЕЖУТКОВ ВРЕМЕНИ
Выводы:1
c и
υ
0
c
, то
2
1 1
c
, тогда
– классическая физика
.
2 υ ~ c и чем больше скорость , тем
3
Неподвижному наблюдателю процессы в
движущейся СО кажутся замедленными.
29. 4) РЕЛЯТИВИСТСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ
Запишем преобразования Лоренца в дифференциалах:dx
dx 0 dt
1
02
c2
dy = dy
dz = dz
dt
dt
0
c
1
2
dx
02
c2
Разделим dx, dy и dz на dt:
30.
dxdt
0
d x 0 dt
dx
dt
x 0
x
0
dx
dt
dt 20 dx dt 1 20
1
2 x
c
c
c dt
2
0
dy
dt
dy 1 2
1 2 y 1 02
dy
c
c dt
c
y
0 x
dt
0 x
dt 20 dx
1
dt 1 2
c
c2
c
02
2
2
0
dz
0
dt
dz 1 2
1 2 z 1 2
dz
c
c dt
c
z
0 x
dt
0 x
dt 20 dx
1
dt 1 2
c
c2
c
02
2
31.
Получаем:x 0
x
0
1 2 x
c
2
y 1 02
c
y
0 x
1 2
c
2
z 1 02
c
z
0 x
1 2
c
Релятивистская теорема о
сложении скоростей
32. СЛЕДСТВИЯ
1 Еслиυ0 c
, тогда получаем
υx υ x υ0
– классический закон сложения
скоростей
2 Пусть частица (фотон, нейтрино) движется в СО К
x c , то
со скоростью
x
c 0 c (c 0 )
c
c
c 0
1 02
c
.
Если частица движется относительно ИСО со скоростью света с, то
относительно любой другой ИСО она также движется со
скоростью с, что подтверждает 2-ой постулат СТО.
33. 4. Интервал
34.
• В обычном пространстве расстояниеопределяется выражением:
2
l между двумя точками
l x y 2 z 2
Это расстояние не зависит от выбора системы координат, т.е. является
инвариантной величиной. При переходе к другой координатной системе
изменяются величины x, y и z, однако эти изменения таковы, что расстояние
l остается одним и тем же.
• Расстояние между двумя мировыми точками называется интервалом
между событиями и определяется выражением:
s c 2 t 2 x 2 y 2 z 2
• Покажем, что интервал между двумя событиями одинаков во всех ИСО,
т.е. он является инвариантной величиной.
• Интервал s является аналогом расстояния l между точками в обычном
пространстве.
• С учетом формулы для l выражение для интервала можно написать в
виде:
2
2
2
s c t l
где l – расстояние между точками обычного пространства, в которых
произошли два события.
35.
• Допустим, что рассматриваются события, происходящие с одной и той жечастицей. Тогда отношение l t дает скорость частицы . Поэтому,
вынеся из-под корня с t , получим:
2
2
l
s c t 1
c t 1 2
c
c t
• Согласно выражению
t 1
2
c2
• - промежуток собственного времени частицы между событиями.
• Таким образом, приходим к соотношению:
s c
• с – скорость света в вакууме, постоянная величина;
• - промежуток собственного времени частицы между событиями
является инвариантной величиной.
• Следовательно, интервал s также является инвариантной величиной.
36. 5. Релятивистская динамика
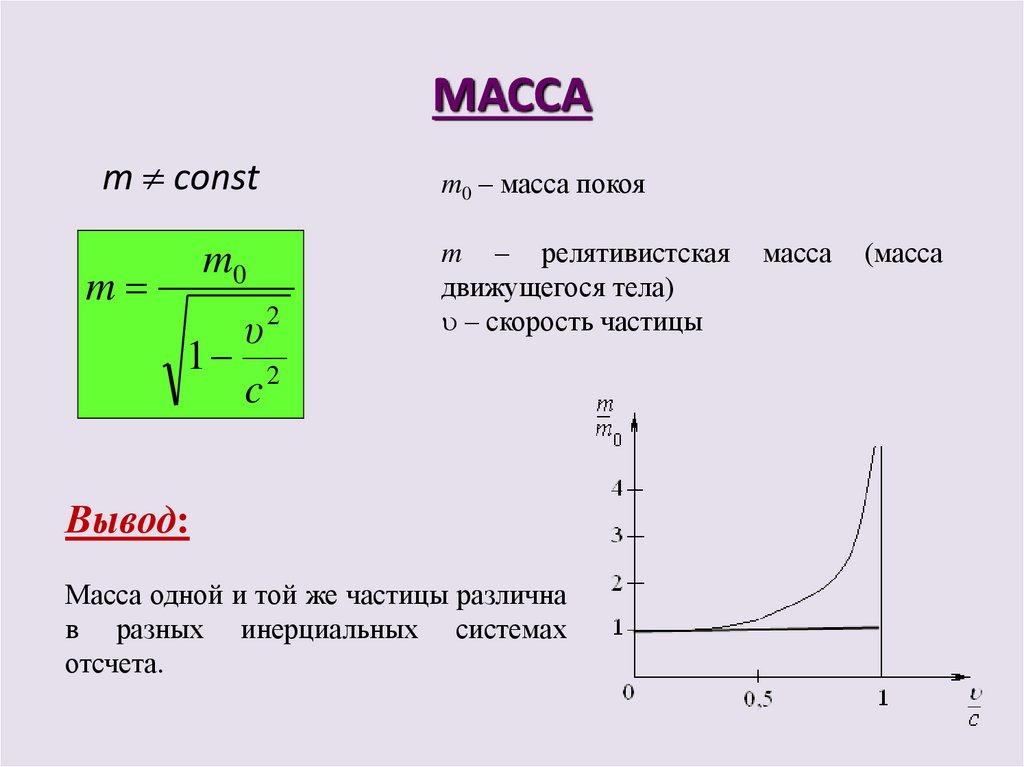
37. МАССА
m constm
m0
υ2
1 2
c
m0 – масса покоя
m – релятивистская
движущегося тела)
– скорость частицы
Вывод:
Масса одной и той же частицы различна
в разных инерциальных системах
отсчета.
масса
(масса
38.
• Из принципа относительности Эйнштейна следует, что математическаязапись любого закона физики должна быть одинаковой во всех ИСО, т.е.
следует условие инвариантности уравнений физических законов
относительно преобразований Лоренца.
• Основной закон классической динамики Ньютона для материальной
точки
d
F
m
a
m
F
или
a
dt
m
• в котором масса m точки считается постоянной и одинаковой во всех
ИСО.
Данное
уравнение
оказывается
неинвариантным
к
преобразованиям Лоренца. Следовательно, эта запись закона не может
служить основой релятивистской динамики.
• Вторая запись основного закона динамики Ньютона
dp
F
dt
• оказывается инвариантной по отношению к преобразованиям Лоренца,
если в нем справа стоит производная по времени от релятивистского
импульса.
39.
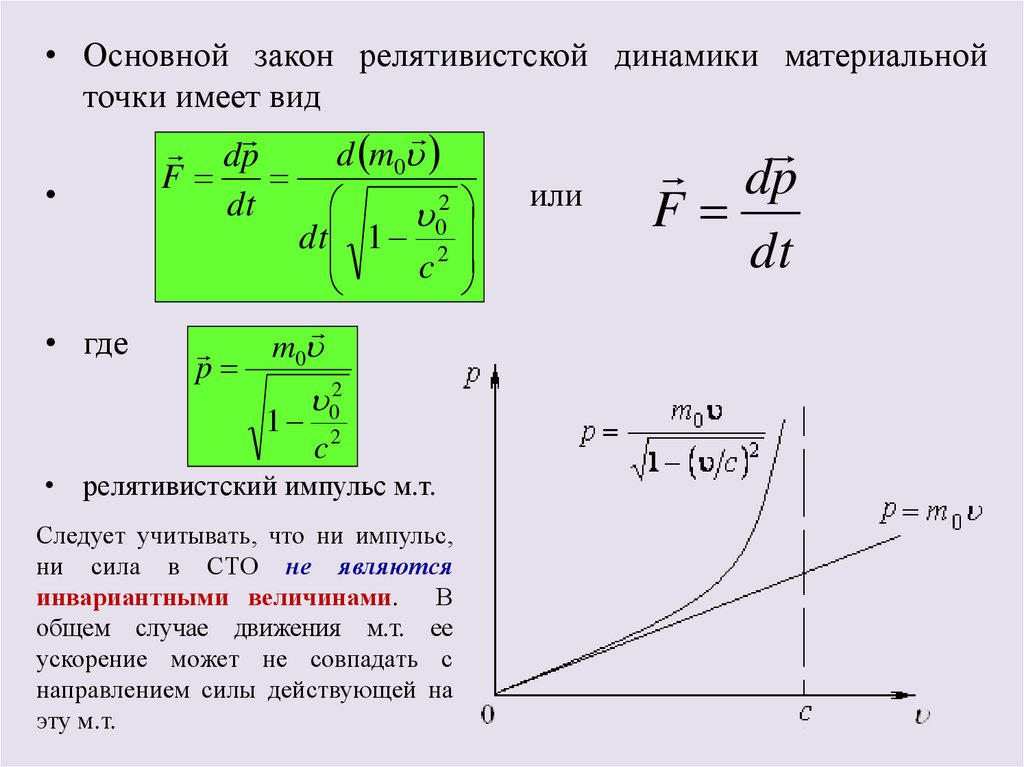
• Основной закон релятивистской динамики материальнойточки имеет вид
dp
d m0
F
d
p
или
2
dt
F
0
dt 1 2
dt
c
• где
p
m0
1
02
c2
• релятивистский импульс м.т.
Следует учитывать, что ни импульс,
ни сила в СТО не являются
инвариантными величинами. В
общем случае движения м.т. ее
ускорение может не совпадать с
направлением силы действующей на
эту м.т.
40.
• В релятивистской механике в силу однородности пространствавыполняется закон сохранения релятивистского импульса:
релятивистский импульс в замкнутой системы сохраняется, т.е. не
изменяется с течением времени.
• Примечание.
• Для тел движущихся со скоростями, близкими к скорости света с,
необходимо использовать только релятивистское выражение для
импульса.
• Следствия:
• 1 при c , m m0 ;
• 2 при c масса m неограниченно возрастает.
Со скоростью c движутся частицы, масса покоя которых m0 = 0. Для
других тел c , c .
• 3 при c , основной закон релятивистской динамики переходит во
второй закон Ньютона. Следовательно, законы классической механики
получаются как следствие теории относительности для предельного
случая c .
41. 6. Закон взаимосвязи массы и энергии
42. закон взаимосвязи массы и энергии
Уравнение E mc 2 используется при изучениистроения атома и в ядерной физике, при
ознакомлении с устройством и работой ядерных
энергетических установок.
Следует отметить, что именно на основании этой
формулы
было
установлено
существование
огромных запасов ядерной энергии и намечены
пути ее «высвобождения».
43. АЛЬБЕРТ ЭЙНШТЕЙН
(1879 — 1955) — один из основателейсовременной теоретической физики,
лауреат Нобелевской премии по
физики 1921 года. Он разработал
несколько значительных физических
теорий:
СТО (1905). В её рамках — закон
взаимосвязи массы и энергии E mc 2
Общая теория относительности
(1907-1916)
Квантовая теория фотоэффекта и
теплоемкости и т.д.
44.
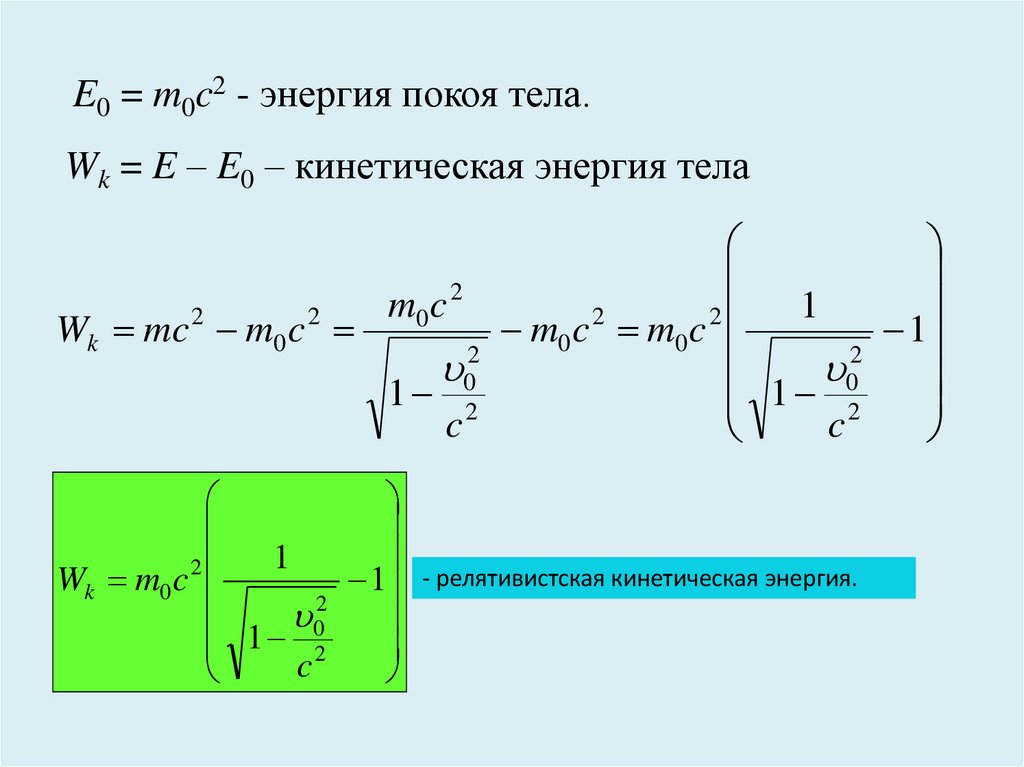
E0 = m0c2 - энергия покоя тела.Wk = E – E0 – кинетическая энергия тела
2
m0 c
1
2
2
2
2
Wk mc m0 c
m0 c m0 c
1
2
2
0
0
1 2
1
2
c
c
1
2
Wk m0 c
1
2
1 0
2
c
- релятивистская кинетическая энергия.
45.
Рассмотрим движение со скоростями 0 << c.Используем известное из математики приближение:
1
1
1 x
2
1 x
x 0
где
x
02
c
2
0
Отсюда следует
2
2 2
2
m
c
m
1
0
0
0
0 0
Wk m0 c 2 1
1
2
2
2
2
c
2
c
Вывод:
При движении с малыми скоростями ( 0 << c) формулы релятивистской
механики переходят в формулы классической механики. Таким образом,
классическая механика является частным случаем релятивистской
механики.
46.
Возведем в квадрат выражение E = mc2:E 2 m 2c 4
m02 c 4
1
c
2
0
2
2
2
m02 c 4 1 02 02
c c
1
02
c2
2 4 2
m
2 4
0 c 0
m0 c
2
0
2
c 1 2
c
m02 c 4 m 2 c 2 02 m02 c 4 pc2
Извлечем квадратный корень
E c
2 2
m0 c
p
2
- связь полной энергии с релятивистским
импульсом.
47.
Инвариантные и неинвариантные величины вСТО
Неинвариантные
Инвариантные
1. Траектория.
2. Радиус-вектор.
1. Скорость света в вакууме.
2.
Скорость
частиц,
обладающих массой покоя.
3. Скорость тел, обладающих массой 3. Масса покоя.
покоя.
4. Импульс.
4. Собственная длина тела.
5. Релятивистская масса.
5. Собственное время.
6. Сила.
6. Электрический заряд
7. Момент импульса.
7. Причина и следствие.
8. Энергия.
8. Интервал
9. Одновременность событий.
10. Длительность событий и ход
времени.
11. Длина.
не
48. 7. Границы применимости классической механики
49.
• Законы ньютоновской механики не допускают существование частиц снулевой массой. Такие частицы под действием ничтожно малой силы
получали бы бесконечно большое ускорение.
• Существование частиц с m = 0 не противоречит законам релятивистской
механики.
m0
• Согласно формуле
p
1
02
c2
• частица с m = 0 может обладать отличным от нуля импульсом лишь в том
случае, если = c, то в формуле для релятивистского импульса
отношение 0/0 представляет собой неопределенность, которая может
равняться конечному числу. Таким образом, частицы с нулевой массой
могут существовать, только двигаясь со скоростью света с.
• Для такой частицы справедливо соотношение
E
p
c
• К частицам с нулевой массой принадлежит фотон.
50.
• Область, в которой ньютоновская механика оказывается справедливой,ограничена релятивистскими и квантовыми эффектами.
• Скорости движений, с которыми мы имеем дело в повседневной жизни и
в технике, настолько малы по сравнению со скоростью света, то
применительно к этим движениям ньютоновскую механику можно
считать практически строгой. При скорости v = 0,1с отличие импульса,
вычисленного по формуле
p
m0
1
02
c2
• от ньютоновского импульса составляет всего лишь 0,5 %.
• В мире элементарных частиц скорости, близкие к скорости света,
оказываются обычным явлением. Поэтому к этим частицам
ньютоновская механика неприменима.
51.
Согласно квантовой механике все материальные объекты (частицы) обладают
волновыми свойствами. Поэтому они не могут одновременно характеризоваться
точными значениями координаты (например, х) и соответствующей компонентой
импульса (т. е. рх).
• Предел точности
Гейзенберга:
определяется
соотношением
неопределенностей
x p x
где x – неопределенность координаты, рx – неопределенность иксовой
компоненты импульса,
h
1,05 10 34 Дж с - постоянная Планка.
2
• Заменив импульс
соотношение
произведением
x x
m
массы
на
скорость,
получим
Понятие траектории применимо только к «классической» частице, к которой можно
приписать в каждый момент времени точные значения координаты и скорости. Из
соотношения неопределенностей видно, что чем меньше масса частицы, тем менее
определенными делаются ее координата и скорость и, следовательно, менее
применимым оказывается понятие траектории. Для макроскопических тел
неопределенность координаты и скорости не превосходят практически достижимой
точности измерений этих величин, вследствие чего к таким телам понятие траектории
применимо без всяких оговорок.



























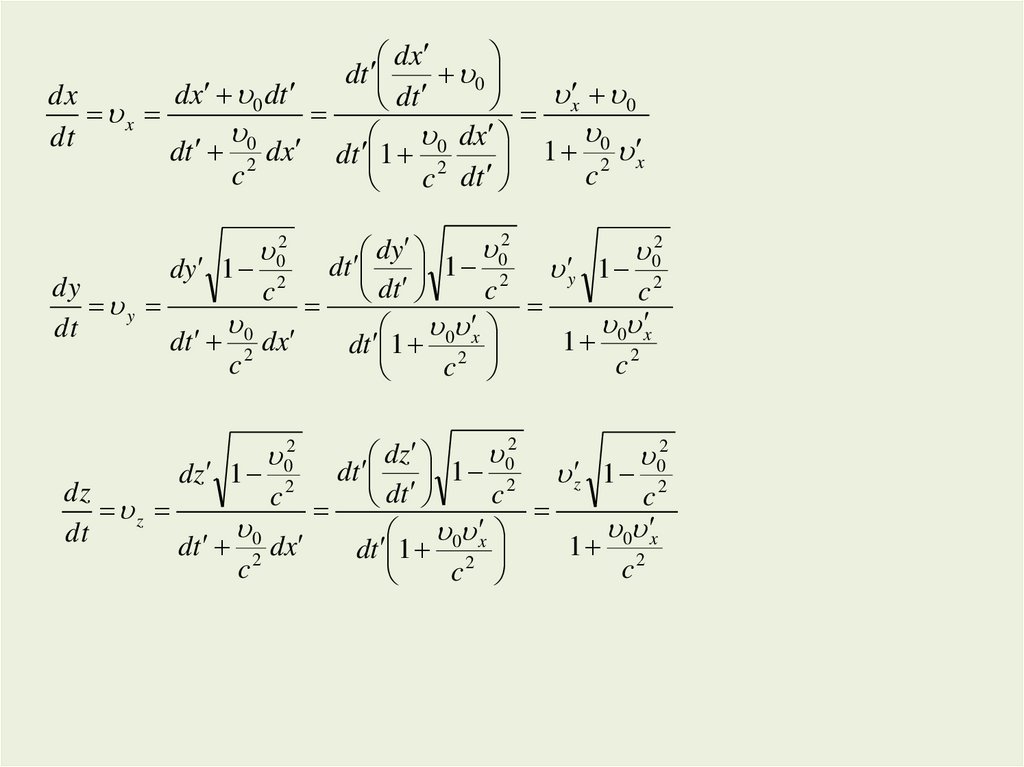


















 physics
physics








