Similar presentations:
Элементы специальной теории относительности (СТО)
1.
Элементы специальной теорииотносительности
(СТО)
СТО описывает специфические эффекты, возникающие при движении тел
со скоростями, сравнимыми со скоростью света
.
Другое название СТО – релятивистская механика.
В СТО, как и в ньютоновской механике, постулируется, что
пространство изотропно и однородно , а время однородно.
2. 1. Преобразования Галилея. Принцип относительности Галилея. Постулаты Эйнштейна.
Рассмотрим две инерциальные системы отсчета (ИСО)и
с
декартовыми системами координат, причем
,
,
а
и
совмещены. Система
неподвижна относительно
наблюдателя, система
движется со скоростью U=const вдоль оси OX.
Выполняется основной постулат классической механики: время во всех
инерциальных системах отсчета течет одинаково, т.е.
.
В начальный момент времени
начала координат
совпадают.
Положение материальной точки P
относительно систем отсчета K и K
в момент времени t будет
описываться соотношением:
r t r t u t
Рис.1
(1)
3. Или в координатной и временной записи:
r t r t u tИли в координатной и временной
записи:
(1)
x x u t,
y y ,
z z ,
t t .
(2)
Выражения (1) и (2) называются преобразованиями Галилея и позволяют,
зная состояние материальной точки в одной инерциальной системе
отсчета , описывать состояние этой точки в другой инерциальной системе
отсчета.
Дифференцирование по времени выражения (1) дает классический закон
сложения скоростей:
. (3)
t t u
При дифференцировании выражения (3) с учетом
.
a = a
получим
.
(4)
4. Из равенства (4) следуют два важных вывода: 1. Любая система отсчета , движущаяся относительно некоторой инерциальной системы
a = a(4)
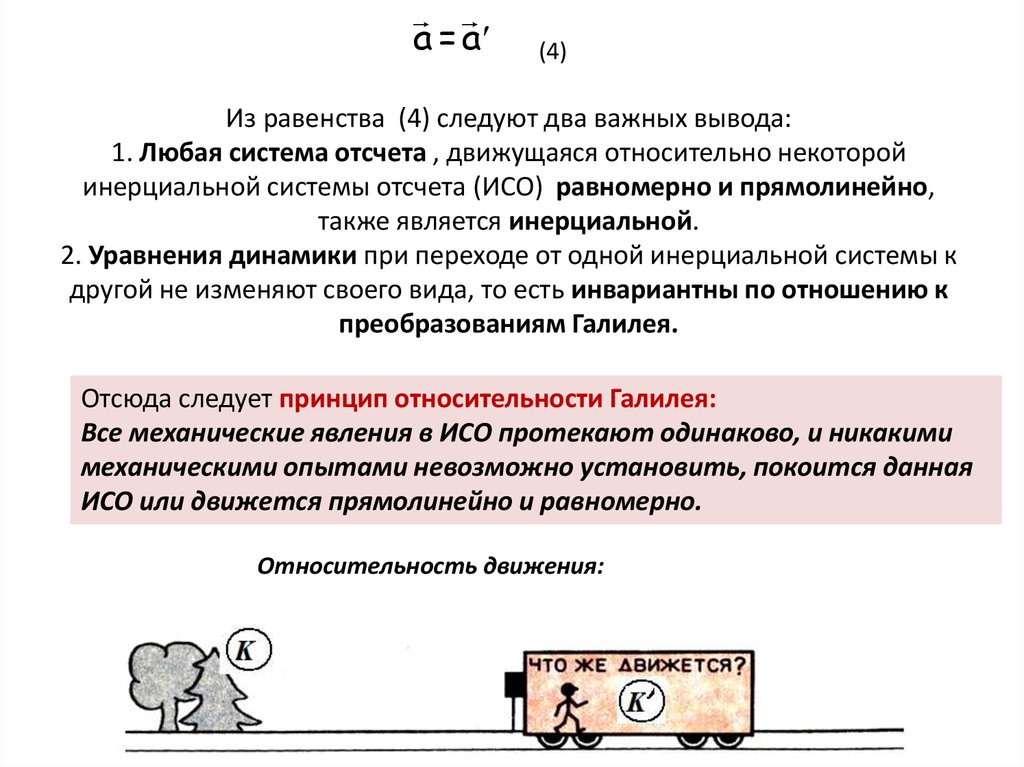
Из равенства (4) следуют два важных вывода:
1. Любая система отсчета , движущаяся относительно некоторой
инерциальной системы отсчета (ИСО) равномерно и прямолинейно,
также является инерциальной.
2. Уравнения динамики при переходе от одной инерциальной системы к
другой не изменяют своего вида, то есть инвариантны по отношению к
преобразованиям Галилея.
Отсюда следует принцип относительности Галилея:
Все механические явления в ИСО протекают одинаково, и никакими
механическими опытами невозможно установить, покоится данная
ИСО или движется прямолинейно и равномерно.
Относительность движения:
5.
Из классического закона сложения скоростей (3) следует, что скоростьсвета должна существенным образом зависеть от относительной скорости
движения источника и приемника света, а, значит, в различных
инерциальных системах отсчета скорость света должна быть различной.
Однако многочисленные опыты по измерению скорости света в различных
условиях давали неизменный результат: скорость света не зависит от
относительного движения источника и приемника света, то есть в любых
инерциальных системах отсчета скорость света имеет универсальное,
неизменное значение. Самым известным из этих опытов является опыт
Майкельсона – Морли.
Рассмотрим сначала аналогию.
AB AC l.
Лодка 1 идет из А в В и обратно ( по
прямой) за время t1 .
Лодка 2 идет из А в С и обратно за
время t 2 .
6.
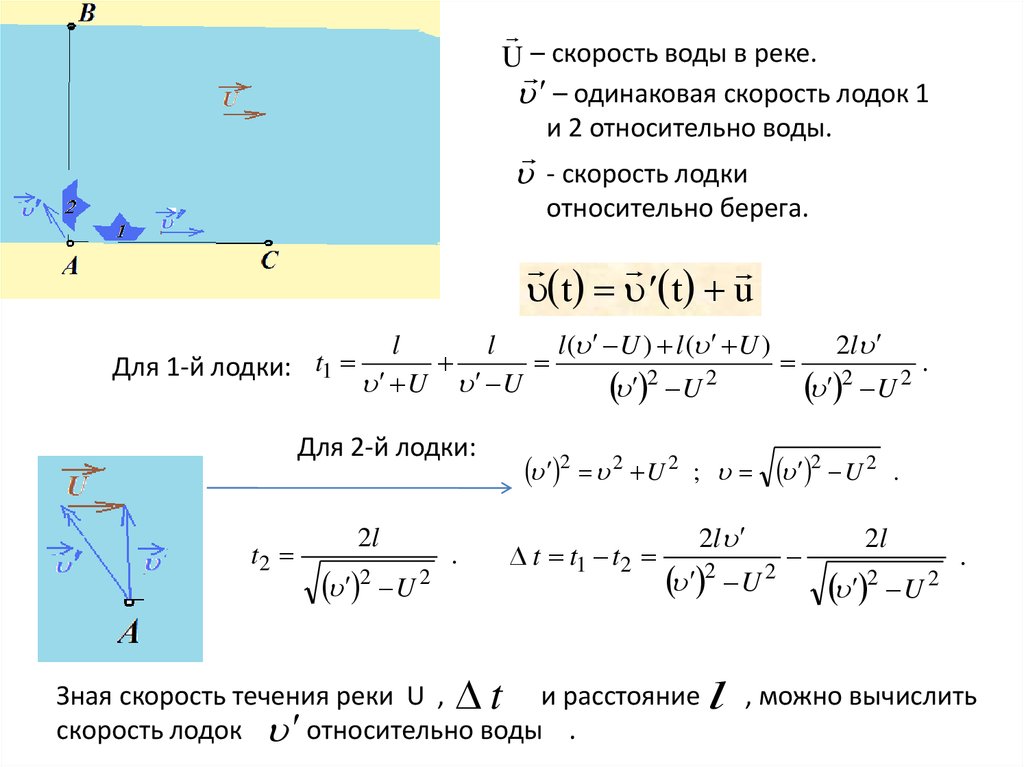
U – скорость воды в реке.– одинаковая скорость лодок 1
и 2 относительно воды.
- скорость лодки
относительно берега.
t t u
Для 1-й лодки: t1
l
l
l ( U ) l ( U )
2l
.
2
2
2
2
U U
U
U
Для 2-й лодки:
t2
2l
2
U
2
.
2 2 U 2
t t1 t2
;
2l
2 U 2
2
2
U
.
2l
2
U
2
.
Зная скорость течения реки U , t и расстояние l , можно вычислить
скорость лодок относительно воды .
7.
Опыт Майкельсона – Морли. В конце 19 века считалось, что все пространствозаполнено единой средой – эфиром, в котором движутся все небесные тела и
распространяется свет. Было известно, что свет распространяется в
пространстве со скоростью около 300 000 км/с . Опыт был поставлен с целью
обнаружить эту среду – эфир.
Предположим, что Земля движется в эфире со скоростью U км/с в направлении
от С к А. С точки зрения земного наблюдателя, эфир движется со скоростью U
км/с от А к С (см. рис.). К концам 2-х жестких стержней АС и АВ прикреплены
зеркала, обращенные к точке А.
8.
В один и тот же момент времени из Апосылаются два световых сигнала вдоль
АС и АВ, которые отражаются от зеркал
обратно к А. Оба сигнала вернулись в А
одновременно: получили t1 t2 , или
t 0.
В дальнейшем в роли АВ были
испробованы разные направления,
результат был то т же.
После усовершенствования методики погрешность измерения скорости
света составляла 200 м/с. Эфира не обнаружили.
Из опыта следует, что в любых инерциальных системах отсчета скорость
света имеет универсальное, неизменное значение:
8
c 3 10 м / с.
9.
Объяснение опытных фактов, противоречащих классической механике,было дано А. Эйнштейном в рамках релятивистской механики (СТО) .
В основе СТО лежат два постулата.
1.Принцип относительности Эйнштейна:
Любое физическое явление независимо от его природы протекает
одинаково во всех инерциальных системах отсчета.
Это означает, что не только с помощью механических опытов (см.
принцип относительности Галилея), но и с помощью любых опытов
невозможно выделить какую-либо одну инерциальную систему отсчета, по
сравнению с другой: все они совершенно равноправны.
2.Принцип постоянства (инвариантности) скорости света:
Скорость света в вакууме не зависит от относительной
скорости источника света и его приемника и одинакова во всех
инерциальных системах отсчета.
Т.е. преобразования Галилея не годятся для описания релятивистских
процессов.
10. 2. Преобразования Лоренца.
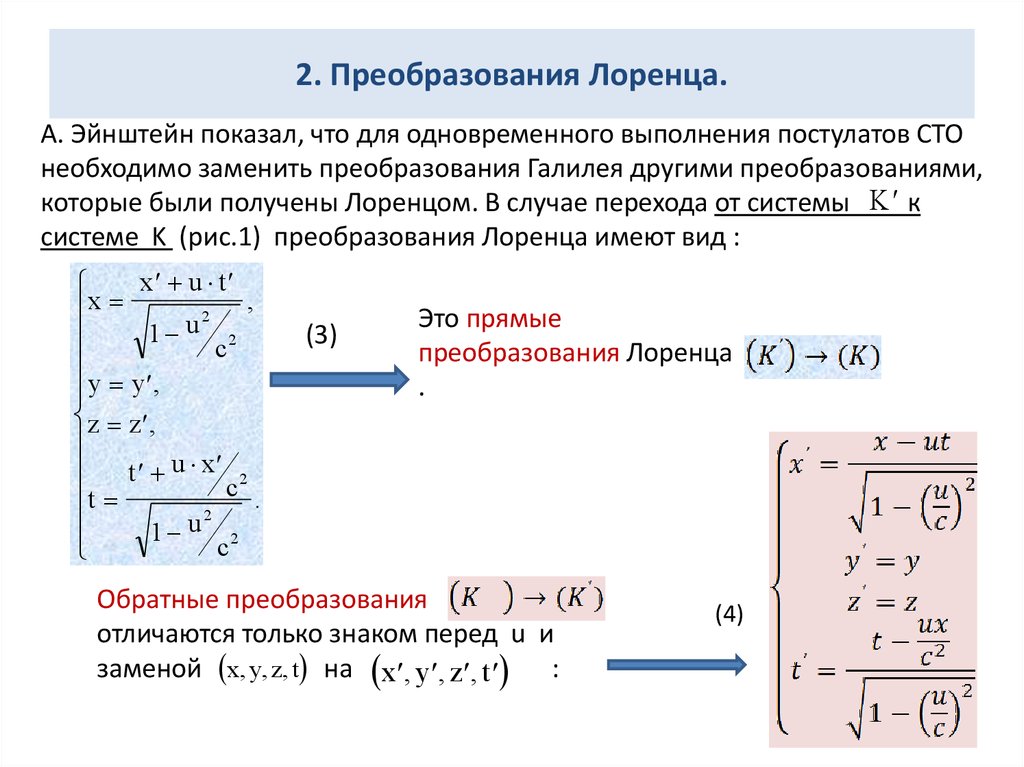
А. Эйнштейн показал, что для одновременного выполнения постулатов СТОнеобходимо заменить преобразования Галилея другими преобразованиями,
которые были получены Лоренцом. В случае перехода от системы K к
системе K (рис.1) преобразования Лоренца имеют вид :
x u t
x
,
2
1 u 2
c
y y ,
z z ,
t u x 2
c .
t
2
u
1
c2
(3)
Это прямые
преобразования Лоренца
.
Обратные преобразования
отличаются только знаком перед u и
заменой x, y, z, t на x , y , z , t :
(4)
11. Рассмотрим предельные случаи прямых преобразований (3):
x u tx
,
2
1 u 2
c
y y ,
z z ,
t u x 2
c .
t
2
u
1
c2
1. При малых скоростях
в пределе
преобразования Лоренца переходят в
преобразования Галилея.
2.
преобразования теряют физический смысл.
12. 3. Следствия из преобразований Лоренца.
3.1 Сокращение длин.Рассмотрим стержень,
расположенный вдоль
OX и покоящийся в системе K` .
Его длина
x x2 x1 0 ,
где
,
-- координаты концов
стержня.
Найдем его длину в системе К :
x x2 x1 ,
где
,
-- координаты концов
стержня, измеренные в один и тот
же момент времени t .
Обозначим
13. Т.о длина тела в направлении движения будет наибольшей в той системе отсчета, где оно покоится. Вывод: пространственные
(4)Из (4):
x1
x1 u t
1
2
; x 2
x x2 x1
Т.к.
x2 u t
1
x2 x1
1
2
2
;
.
x x2 x1 0 , , а x x2 x1 , то
0 1 2 .
Т.о длина тела в направлении движения будет наибольшей в той системе
отсчета, где оно покоится.
Вывод: пространственные соотношения зависят от движения,
пространство не является абсолютным.
14. 3.2 Относительность одновременности.
События называются одновременными, если они происходят в один итот же момент времени, измеренный по часам одной системы
отсчета.
Пусть в системе отсчета K` происходят два каких-либо события:
- первое в точке X`1 в момент времени t`1 ,
- второе в точке X`2 в момент времени t`2 .
Для этих событий в системе К из формул преобразований для
времени и координат (3):
ut
x
u
t
x
1
1
u
x
2
2
u x1
2
x
,
x
,
1
t
2
t1
2
2
2
2
2
c
c
1 u 2
1 u 2
t
,
t1
,
2
2
c
c
2
u
1
1 u 2
c2
c
следует , что:
а) если эти события в системе K пространственно совмещены (X`1 =X`2) и
происходят одновременно (t`1=t`2), то в К они будут одновременны и будут
происходить в одном месте ( t1 t2 , x1 x2 ) .
б)если события происходят в разных точках системы K` (X`1≠X`2) , но одновременны
(t`1=t`2), то они уже не будут одновременны в системе К. t 2 t1
15.
Выразим временной интервал Δt=t2-t1 в системе К между событиями,одновременными в системе Кʹ:
u x 2
u x1
2
t
t1
2
2
c
c
t2
,
t1
,
2
2
1 u
1 u
2
c2
c
t 2 t1
x2 x1 u c 2
1 u
2
0
c2
Временной интервал Δt=t2-t1 зависит от скорости ИСО K` и разности координат
ΔX`=X`2 - X`1
Одновременность в механике релятивистских скоростей понятие
относительное.
Но! Если события связаны причинно-следственной связью, то они никогда не будут
одновременны. В любой системе отсчета причина всегда будет предшествовать
следствию.
16. 3.3 Замедление хода часов.
Пусть в системе К’ точке X` произошли два события с интервалом времени
(две вспышки света). Это собственное время между событиями .
t t2 t1
x1 x2 x`.
Используем преобразования (3) :
x u t
x
,
2
u
1
c2
y y ,
z z ,
t u x 2
c .
t
u2 2
1
c
В системе К события происходят в разных точках - X1 И X2 в моменты времени:
u x
u x
t1 2
t2 2
c
c ,
t1
,
t
2
1 2
1 2
Интервал между событиями в с.о. К:
t t2 t1
t2 t1
1
2
t
1
2
,
17. Или:
Перепишем:t
t
1 2
,
Или:
t t
Промежуток времени между событиями наименьший в той С.О., где
события происходят в одном месте.
Т.о. время в разных системах отсчета течет по разному.
18.
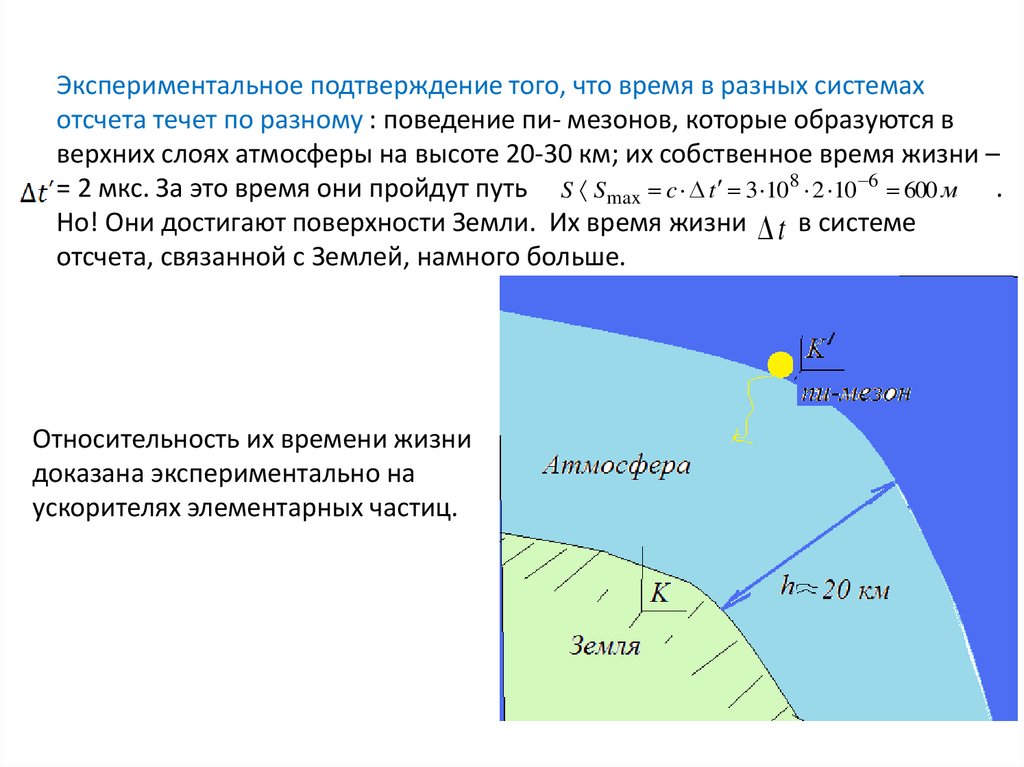
Экспериментальное подтверждение того, что время в разных системахотсчета течет по разному : поведение пи- мезонов, которые образуются в
верхних слоях атмосферы на высоте 20-30 км; их собственное время жизни –
= 2 мкс. За это время они пройдут путь S Smax c t 3 108 2 10 6 600 м .
Но! Они достигают поверхности Земли. Их время жизни t в системе
отсчета, связанной с Землей, намного больше.
Относительность их времени жизни
доказана экспериментально на
ускорителях элементарных частиц.
19.
Пространственно-временной интервалВзаимосвязь пространства и времени в СТО удобно представлять в виде
четырехмерного пространства, в котором событие характеризуется 4-мя
координатами: x,y,z,t. Если в системе К начало процесса происходит в точке
x1, y1, z1, t1 , а его конец в точке x2 , y2 , z2 , t2 , то интервал между двумя
событиями
S 2 c2 t 2 x 2 y 2 z 2
, где
t t2 t1 , x x2 x1 , y y2 y1 , z z2 z1 .
S 2 c2 t 2 r 2 , где r - расстояние между точками
Или
обычного 3-хмерного пространства.
В системе K
S 2 c2 t 2 x 2 y 2 z 2
С помощью преобразований Лоренца можно показать, что пространственновременной интервал S инвариантен относительно всех ИСО, то есть
S 2 S 2
, или
c 2 t 2 x 2 y 2 z 2 c 2 t 2 x 2 y 2 z 2
20. 4. Закон сложения скоростей в релятивистской механике.
Установить видпреобразования скорости в
dx
релятивистском случае можно
дифференцированием
преобразований Лоренца.
Находим полные
дифференциалы координат в
(3) и делим на dt:
x u t
x
,
2
1 u
c2
y y ,
(3) z z ,
t u x 2
c .
t
u2 2
1
c
dx u dt
2
u
1
c
;
dy dy ;
dz dz ;
2
dt
u
dx
2
c
.
2
1 u 2
c
dt
dx
dx u dt
; (5)
u
dt
dt 2 dx
c
dy
dt
dy 1 u
2
c2
u
dt 2 dx
c
dz
dt
dz 1 u
2
c2 ;
u
dt 2 dx
c
;
(6)
21. учтем, что
Перепишем полученные выражения:dx dx u dt
;
u
dt
dt 2 dx
c
dy
dt
2
u
dy 1
c
2
u
dt 2 dx
c
dz
dt
;
dz 1 u
2
c2 .
u
dt 2 d x
c
Поделим числитель и знаменатель в этих выражениях на dt` ,
dx
dy
dz
dx
dy
dz
x ; y ; z ;
x ;
y ; z .
dt
dt
dt
dt
dt
dt
учтем, что
x u
x
u x
1
c
y
y
2
1
2
u
1
u x
c2 ;
z
c2
z
2
u
1
1
u x
c2
c2
(7)
Обратный переход от К к Кʹ - меняется только знак перед u:
x u
x
u x
1
;
c
2
y
y 1 u
1
u x
2
c2 ;
c
2
z
z 1 u
1
2
u x
c2 .
c2
22. Равенства (7) носят название релятивистского закона сложения скоростей. Рассмотрим предельные случаи этих равенств.
x ux
u x
1
В) Пусть
c2
А) При
переходим к закону
сложения скоростей в классической механике.
Б) Предельная скорость не должна превышать
скорость света (т.е. должен выполняться 2-й
постулат Эйнштейна). Пусть
23.
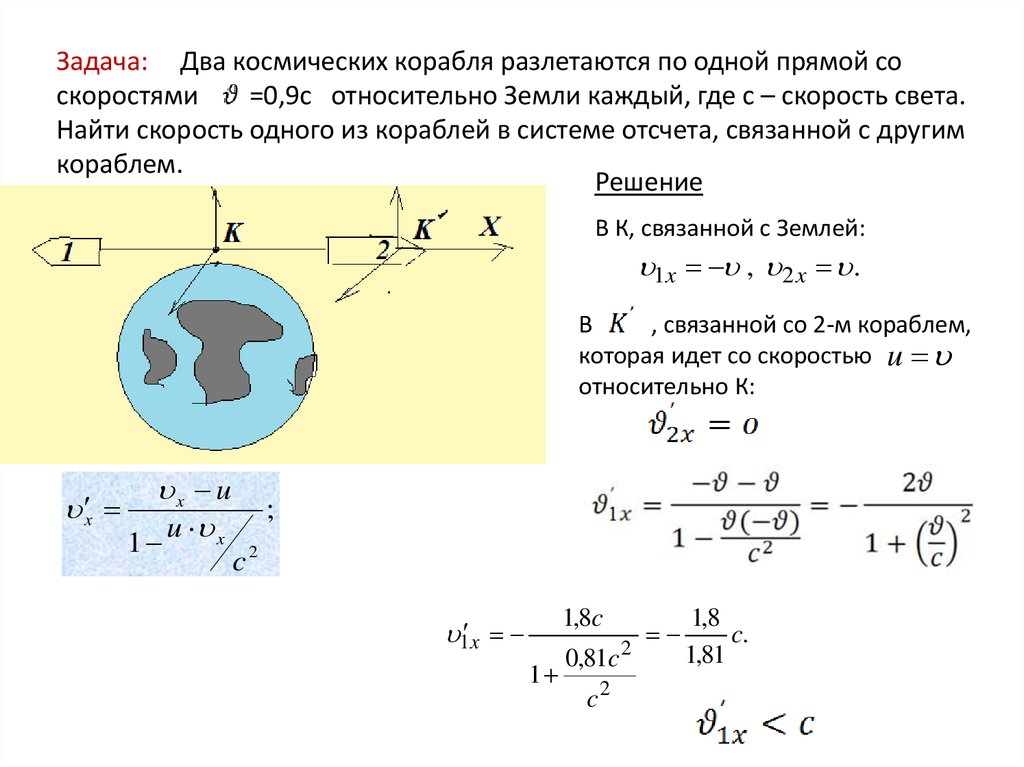
Задача: Два космических корабля разлетаются по одной прямой соскоростями
=0,9c относительно Земли каждый, где с – скорость света.
Найти скорость одного из кораблей в системе отсчета, связанной с другим
кораблем.
Решение
В К, связанной с Землей:
1x , 2 x .
В
, связанной со 2-м кораблем,
которая идет со скоростью u
относительно К:
x
x u
u x
1
;
c2
1,8c
1 x
1
0,81c 2
c2
1,8
c.
1,81
24. 5. Релятивистский импульс. Зависимость массы от скорости.
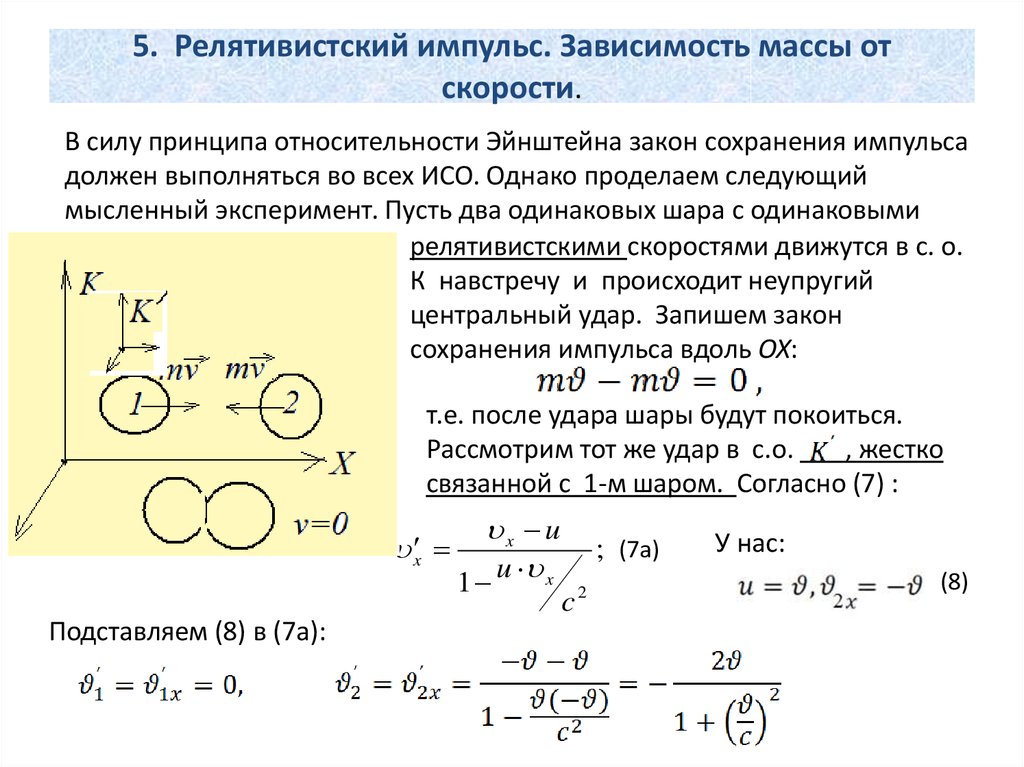
В силу принципа относительности Эйнштейна закон сохранения импульсадолжен выполняться во всех ИСО. Однако проделаем следующий
мысленный эксперимент. Пусть два одинаковых шара с одинаковыми
релятивистскими скоростями движутся в с. о.
К навстречу и происходит неупругий
центральный удар. Запишем закон
сохранения импульса вдоль OX:
т.е. после удара шары будут покоиться.
Рассмотрим тот же удар в с.о.
, жестко
связанной с 1-м шаром. Согласно (7) :
x
Подставляем (8) в (7а):
x u
u x
1
; (7а)
c
2
У нас:
(8)
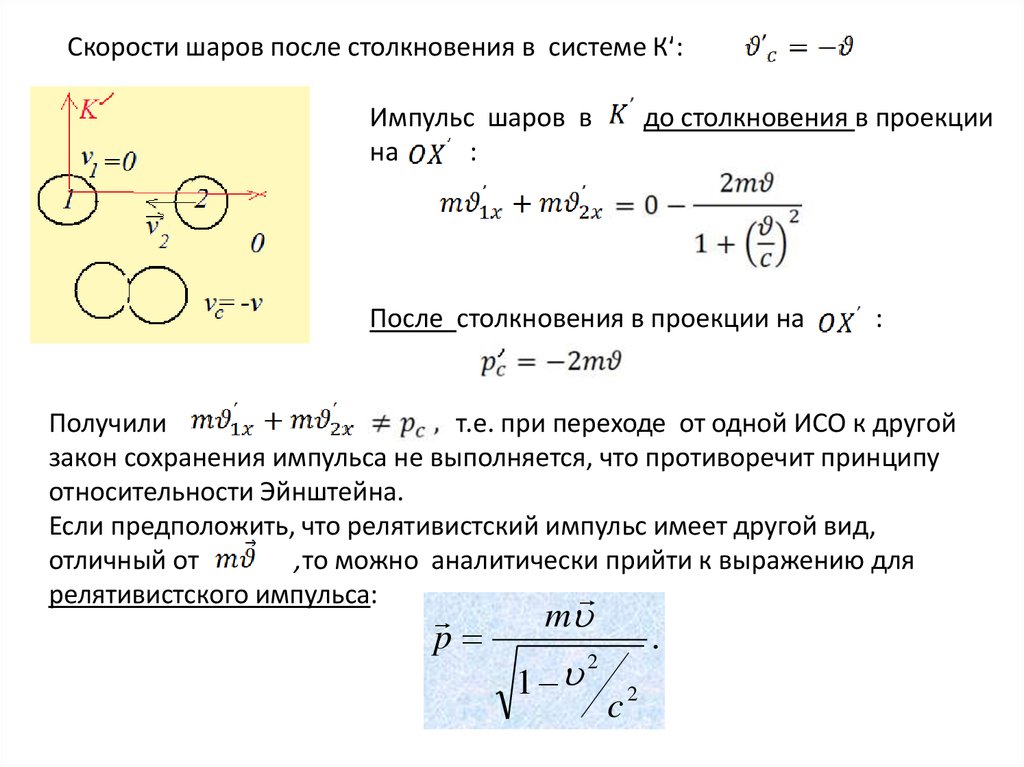
25. Скорости шаров после столкновения в системе Кʹ:
Импульс шаров вна
:
до столкновения в проекции
После столкновения в проекции на
:
Получили
т.е. при переходе от одной ИСО к другой
закон сохранения импульса не выполняется, что противоречит принципу
относительности Эйнштейна.
Если предположить, что релятивистский импульс имеет другой вид,
отличный от
,то можно аналитически прийти к выражению для
релятивистского импульса:
p
m
2
1
.
c2
26. Для этого выражения закон сохранения импульса выполняется при использовании преобразований Лоренца для перехода от К к , а при
pm
1
.
.
2
(9)
c2
Для этого выражения закон сохранения импульса
выполняется при использовании преобразований
Лоренца для перехода от К к
, а при
оно переходит в выражение для
ньютоновского импульса:
.
Если ввести понятие релятивистской массы частицы
mr
m
1
,
2
c2
(10), где
m
,
независящая
от
скорости
величина, называемая массой
покоя, то формально сохраняется
классический вид определения
импульса
p mr
Согласно выражению (10), масса движущегося тела зависит от скорости.
Масса покоя – масса тела, измеренная в той системе отсчета, где тело
покоится.
Под массой понимается мера инертности тела, то есть его
способность сопротивляться движению!
27. Проанализируем выражение (10) для релятивистской массы:
mrm
2
1
,
c2
(10)
Проанализируем выражение (10) для
релятивистской массы:
1) При
Т.е. влияние скорости на массу частицы
становится заметным только при больших скоростях.
2) Если
, то при
Т.е. тела с массой покоя,
отличной от нуля, никогда не смогут достичь скорости света.
3)
Для тел с массой покоя, равной нулю,
возможно движение только со скоростью света (пример - фотоны).
28. 6. Основной закон релятивистской динамики.
dp dm
F
dt
dt 1 2
c2
(11)
-- записанный в таком виде, он выполняется во всех ИСО . При
он переходит в выражение для 2 – го закона Ньютона.
29. 7. Релятивистская энергия.
Пусть на частицу действует некоторая силаF,
которая, очевидно, совершает над частицей при ее перемещении на
работу A F dr
dr
,
что приводит к эквивалентному приращению кинетической энергии частицы
dT A .
Элементарную работу
A
определим, используя (11):
d m
dT A
dt 1 2
dr
Учтя, что dr dt , получим для приращения кинетической энергии:
30.
d mdT
dt 1 2
m
dt d
1 2
.
выполним дифференцирование дроби в правой части:
2
mc d
2
dT
2
2 1 2
c
2
Учтем, что
2
d d .
2
, после чего получим:
Из последнего равенства следует релятивистское выражение для кинетической
энергии частицы
mc
1
T
mc 2 mc 2
1
2
1 2
1 2
2
c
c
2
,которое существенно отличается от классического.
(12)
31.
mc 21
2
2
T
mc mc
1 (12)
2
2
1
1 2
2
c
c
Покажем, что (12) при
переходит в выражение для кинетической
2
энергии ньютоновской механики T m .
2
Для
применим разложение в ряд Тейлора, ограничившись
первыми двумя членами:
.
В нашем случае
.
Тогда
1 2 m 2
1
2
2
T mc
1 mc 1
.
2 1
2
2
c
2
1 2
c
В (12) определяющей является величина
которая
частицы, а
называется
полной
E 0 mc 2
(14)
E
mc 2
2
1
m r c2 ,
(13)
c2
релятивистской энергией
- ее энергией покоя.
32. Выражению (12) с учетом (13) и (14) теперь можно придать другой вид:
Выражению (12) с учетом (13) и (14) теперь можно придать другой вид:.
T E E E 0 m r c mc c m,
2
Приращение полной энергии частицы в виде
2
2
E m r c 2
есть величина, определяющая кинетическую энергию релятивистской частицы.
А. Эйнштейн обобщил это соотношение, сформулировав закон
эквивалентности массы и энергии :
любое изменение массы материального объекта приводит к
соответствующему изменению полной энергии этого объекта и наоборот.
В этом смысле говорят об эквивалентности энергии и массы:
E mr c 2 .
33. 8. Связь релятивистских энергии и импульса частицы.
Emc
2
1
(15)
2
c2
;
p
m
1
. (16)
2
c2
Запишем последнее выражение в скалярной
форме и исключим скорость частицы:
Получим:
E c p 2 m 2c2 .
34. Найдем связь кинетической энергии с импульсом частицы:
.E c p 2 m 2c2 .
Основные выводы СТО:
1) Пространство и время взаимосвязаны (см. преобразования Лоренца) и
образуют единую форму существования материи.
2) Масса и энергия взаимосвязаны (см. закон эквивалентности массы и
энергии Эйнштейна) и образуют единую форму существования материи.
3) Частным случаем релятивистской механики является классическая
механика.
35.
ФакультативВ общей теории относительности свойства пространства-времени
зависят от распределения тяготеющих масс. Гравитация по теории
Энштейна представляет искажение пространства- времени.
Графическая иллюстрация
искривления пространствавремени под воздействием
материальных тел . На ней
изображены геодезические линии.
Слева — незначительная воронка,
образовавшаяся под воздействием
Солнца; в центре — гравитационное
поле более тяжелой нейтронной
звезды; справа — глубокая воронка
без дна, представляющая черную
дыру
36.
Общая теория относительности говорит о влиянии на ход временираспределения гравитационных масс. Например, вблизи
массивных тел время замедляет свой ход, а в центре планет
время течет несколько медленнее, чем на поверхности. Этот
эффект тем заметнее, чем больше масса небесных тел.
37.
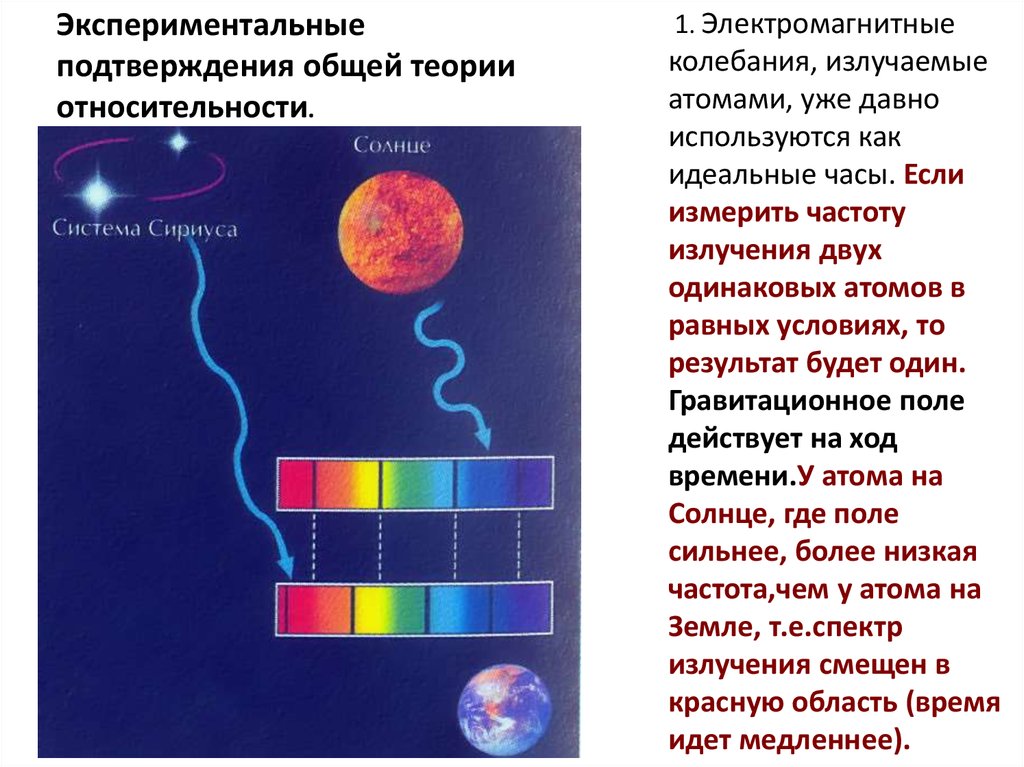
Экспериментальныеподтверждения общей теории
относительности.
1. Электромагнитные
колебания, излучаемые
атомами, уже давно
используются как
идеальные часы. Если
измерить частоту
излучения двух
одинаковых атомов в
равных условиях, то
результат будет один.
Гравитационное поле
действует на ход
времени.У атома на
Солнце, где поле
сильнее, более низкая
частота,чем у атома на
Земле, т.е.спектр
излучения смещен в
красную область (время
идет медленнее).
38.
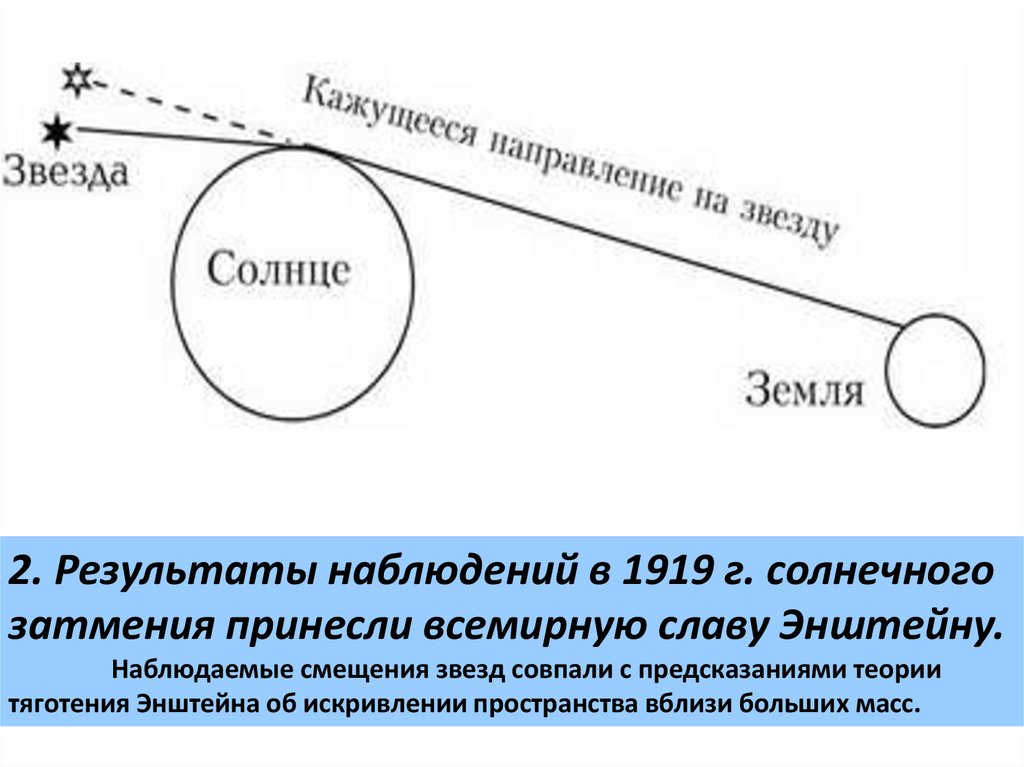
2. Результаты наблюдений в 1919 г. солнечногозатмения принесли всемирную славу Энштейну.
Наблюдаемые смещения звезд совпали с предсказаниями теории
тяготения Энштейна об искривлении пространства вблизи больших масс.





























 physics
physics








