Similar presentations:
Элементы специальной теории относительности (СТО)
1. Элементы специальной теории относительности (СТО)
Лекция: специальная теория относительности и ее следствияЭлементы специальной теории
относительности (СТО)
Кафедра прикладной и теоретической физики
Слайд-конспект лекций по механике
2. Относительность движения. Системы отсчёта
Лекция: специальная теория относительности и ее следствияОтносительность движения. Системы
отсчёта
Понятие движения имеет строго определённое содержание только
при указании, относительно каких именно тел перемещается
рассматриваемый объект. В этом заключается фундаментальное
свойство природы, состоящее в том, что всякое движение
относительно.
Абсолютное движение тела безотносительно к другим телам
лишено смысла.
Поэтому, чтобы изучать движение какого-либо тела нужно указать,
по отношению к каким другим телам происходит данное движение.
Движение происходит не только в пространстве, но и во времени.
Поэтому для описания движения необходимо определять время, что
делается с помощью часов. (Понятие «часы» в физике имеет более
широкий смысл, чем в житейских условиях. Под часами понимается
любой периодический процесс.)
Кафедра прикладной и теоретической физики
Слайд-конспект лекций по механике
3. Пример иллюстрирующий относительность движения
Лекция: специальная теория относительности и ее следствияПример иллюстрирующий относительность
движения
С точки зрения человека находящегося в движущемся
автомобиле траектория движения мяча, который он подбрасывает,
представляет собой отвесную прямую.
Наблюдатель у дороги видит, что траектория мяча – парабола.
Кафедра прикладной и теоретической физики
Слайд-конспект лекций по механике
4. Системы отсчёта
Лекция: специальная теория относительности и ее следствияСистемы отсчёта
Y
V
часы
X
Z Тело отсчёта
Совокупность тела отсчёта (или набора
неподвижных относительно друг друга
тел),
относительно
которого
рассматривается движение, и прибора
для отсчёта времени (часов) называется
системой отсчёта(СО).
Для
количественного
описания
движения с телом отсчёта связывают
систему координат (чаще всего- декартову
систему координат ).
система отсчёта
Кафедра прикладной и теоретической физики
Слайд-конспект лекций по механике
5. Системы отсчёта
Лекция: специальная теория относительности и ее следствияСистемы отсчёта
Систему отсчёта можно выбрать произвольно бесчисленным множеством
способов. Различные СО равноправны и одинаково доступны. Естественно
выбирать СО таким образом, чтобы движение в ней выглядело наиболее
просто. Инерциальные системы отсчёта таковыми и являются.
Инерциальными называются системы отсчёта, в которых выполняется
первый закон Ньютона (закон инерции Галилея).
Первый закон Ньютона гласит: всякое тело находится в состоянии покоя
или равномерного и прямолинейного движения, пока воздействие со
стороны других тел не заставит его изменить это состояние.
Инерциальных систем отсчёта (ИСО) бесконечное множество. Любая
другая система, движущаяся по отношению к инерциальной прямолинейно
и равномерно, также является инерциальной.
Всякая СО, движущаяся ускоренно по отношению к идеальной
инерциальной системе отсчёта, называется неинерциальной.
Кафедра прикладной и теоретической физики
Слайд-конспект лекций по механике
6. Системы отсчёта
Лекция: специальная теория относительности и ее следствияСистемы отсчёта
• ИСО принято подразделять на ЛСО (лабораторная СО) и СЦИ
(система центра инерции).
• СЦИ- система отсчёта, в которой суммарный импульс частиц
(тел) всегда равен нулю.
Таким образом:
система отсчёта
ИСО
ЛСО
Не ИСО
СЦИ
Кафедра прикладной и теоретической физики
Слайд-конспект лекций по механике
7. Инерциальные системы отсчёта
Лекция: специальная теория относительности и ее следствияИнерциальные системы отсчёта
Идеальной инерциальной системой отсчёта является СО
связанная со свободным телом, то есть с телом, находящемся
настолько далеко от всех остальных, что оно не испытывает
воздействие со стороны последних.
Реальные СО - неинерциальные (Не ИСО).
Если неинерциальность данной СО несущественна для
рассматриваемых в ней явлений, то эту СО можно условно
считать инерциальной.
На практике чаще всего применяется две достаточно хороших
инерциальных системы отсчёта:
- геоцентрическая, в которой за тело отсчёта принимается
Земля;
- гелиоцентрическая, в которой телом отсчёта является
Солнце.
Геоцентрическая СО менее инерциальная, чем
гелиоцентрическая СО.
Кафедра прикладной и теоретической физики
Слайд-конспект лекций по механике
8. Принцип относительности и преобразования Галилея
Лекция: специальная теория относительности и ее следствияПринцип относительности и преобразования
Галилея
ИСО являются выделенными по сравнению с неинерциальными.
Это связано с одним из фундаментальных законов природы –
принципом относительности (ПО):
Все законы физики одинаковы во всех инерциальных системах отсчёта, т.е.
имеют одинаковую форму и значение констант, входящих в эти законы.
Это современная формулировка ПО данная Эйнштейном .
Впервые ПО был установлен Галилеем для законов классической механики и
называется принципом относительности Галилея:
Все законы механики одинаковы во всех инерциальных системах отсчёта.
При переходе от одной ИСО к другой координаты тел, их скорости и другие
величины изменяются. Поэтому необходимо знать правила перехода из
одной ИСО в другую, т.е. как выражаются величины в одной ИСО через те
же величины в другой.
Для вывода этих правил в классической ньютоновской механике принимались
следующие допущения:
• Преобразования должны находиться в соответствии с ПО;
• Время во всех ИСО течёт одинаково, т.е. носит абсолютный характер.
• Пространство однородно и изотропно, а время однородно.
Эти представления соответствовали всей совокупности экспериментальных
данных, имеющихся в то время (семнадцатый век).
Кафедра прикладной и теоретической физики
Слайд-конспект лекций по механике
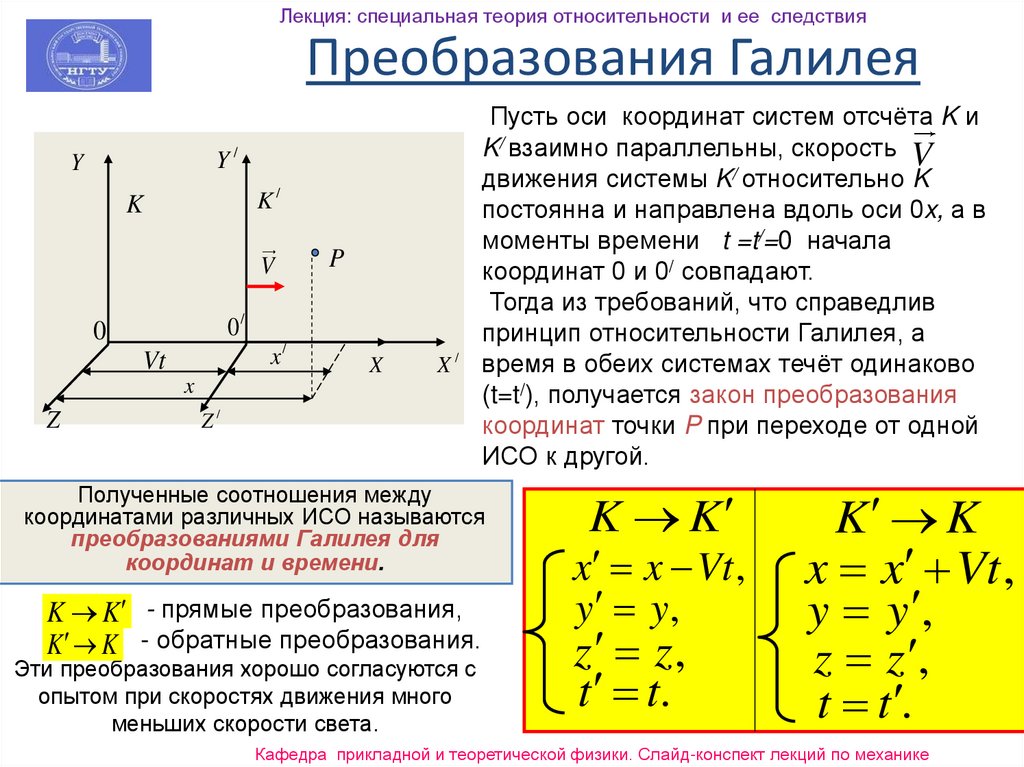
9. Преобразования Галилея
Лекция: специальная теория относительности и ее следствияПреобразования Галилея
Y/
Y
K/
K
V
P
0/
0
x/
Vt
X
X/
x
Z
Z/
Пусть оси координат систем отсчёта K и
K/ взаимно параллельны, скорость V
движения системы K/ относительно K
постоянна и направлена вдоль оси 0x, а в
моменты времени t =t/=0 начала
координат 0 и 0/ совпадают.
Тогда из требований, что справедлив
принцип относительности Галилея, а
время в обеих системах течёт одинаково
(t=t/), получается закон преобразования
координат точки P при переходе от одной
ИСО к другой.
Полученные соотношения между
координатами различных ИСО называются
преобразованиями Галилея для
координат и времени.
K K - прямые преобразования,
K K - обратные преобразования.
Эти преобразования хорошо согласуются с
опытом при скоростях движения много
меньших скорости света.
K K
x x Vt ,
y y,
z z,
t t.
K K
x x Vt ,
y y ,
z z ,
t t .
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
10. Классический закон сложения скоростей
Лекция: специальная теория относительности и ее следствияКлассический закон сложения скоростей
Пусть точка Р движется со скоростью v относительно системы K, а
относительно системы K/ - cо скоростью v .
Найдём связь между ними. Для этого продифференцируем
уравнения Галилея по времени, учтя, что t=t/и значит dt=dt/.
dx dx
dx
V
V , т.е. vx v x V ,
dt dt
dt
Здесь vx - проекция скорости точки на ось x,
v x - проекция скорости точки на ось x/.
dy dy
,
т.е.
v
v
y
y
dt dt
dz dz
т.е. vz v z ,
,
dt dt
Или в векторной форме:
v v V .
Это и есть классический закон сложения скоростей или закон
преобразования скорости точки (тела) при переходе от K/ к K.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
11. Следствия из преобразований Галилея
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Галилея
Помимо закона сложения скоростей к важным следствиям
преобразований Галилея относятся также следующие:
• Ускорения тел во всех инерциальных системах отсчёта одинаковы.
Действительно, дифференцируя по t с учётом того, что t=t/ и скорость
постоянна получаем:
dv d (v V ) dv dv
a
a .
dt
dt
dt dt
• Расстояние между двумя точками во всех ИСО одинаковы.
Значит одинаковы и размеры тел.
• Из этих следствий вытекает, что силы взаимодействия между
телами (частицами) тоже одинаковы во всех ИСО: F F
Величины, которые имеют одно и то же числовое значение во всех
системах отсчёта, называются инвариантными или инвариантами
преобразований.
В рамках этой терминологии ускорения, размеры тел, промежутки
времени, силы – инварианты преобразований Галилея.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
12. Трудности ньютоновской физики. Скорость света
Лекция: специальная теория относительности и ее следствияТрудности ньютоновской физики.
Скорость света
В середине 19-ого века были разработаны методы
достаточно точного измерения скорости света. Оказалось,
что в вакууме она составляет
c 3 108 м / с
Напрашивается вопрос: к какой СО относится это значение?
Из классического закона сложения скоростей вытекает, что в
разных СО скорость света должна быть разной (см. Рис.
справа): по отношению к СО, догоняющей свет, она должна
быть меньше, чем по отношению к покоящейся СО; по
отношению к СО убегающей от источника скорость света
должна быть больше, чем по отношению к покоящейся СО и
т.д. На самом деле в экспериментах этого не наблюдалось.
Опыты по измерению скорости света в движущихся СО
показали, что во всех ИСО эта скорость имеет одно и то же
значение, т.е. скорость света – инвариантная величина.
Впервые постоянство скорости света было обнаружено в
опытах Майкельсона и Морли (Рис. слева). Движущейся СО
служила Земля. Сравнивалась скорость света вдоль направления
движения Земли по околосолнечной орбите со скоростью света
поперёк этого направления. Оказалось, что «поперечная» и
«продольная» скорости света равны.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
13. Трудности ньютоновской физики. Скорость света
Лекция: специальная теория относительности и ее следствияТрудности ньютоновской физики.
Скорость света
На рисунке показан ещё один вариант опытов по
измерению скорости света в движущихся СО. Результат,
как и в опытах Майкельсона: скорость света – инвариант.
Из всех опытов следует также, что скорость света в
вакууме является предельной. Никакой сигнал, никакое
воздействие тел друг на друга не могут распространяться
со скоростью, превышающей скорость света в вакууме.
Это противоречит ньютоновскому принципу
дальнодействия, согласно которому взаимодействие тел
распространяется мгновенно, то есть с бесконечно
большой скоростью.
Был сделан целый ряд попыток объяснения результатов опыта Майкельсона и
Морли и аналогичных ему в рамках ньютоновской классической механики.
Однако все они оказались в конечном счёте неудовлетворительными.
Кардинальное решение этой проблемы было дано в теории относительности
Эйнштейна. Для этого понадобился существенный пересмотр представлений о
пространстве и времени.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
14. Эйнштейн – отец теории относительности
Лекция: специальная теория относительности и ее следствияЭйнштейн – отец теории относительности
В1905 году Альберт Эйнштейн
создал
специальную
теорию
относительности (СТО),
которая
представляет собой физическую
теорию пространства и времени .
СТО часто называется
также
релятивистской
теорией,
а
специфические
явления,
описываемые
этой
теорией,релятивистскими эффектами.
Большинство релятивистских эффектов (но не все)
проявляются, когда тело движется со скоростью близкой
к скорости света.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
15. Постулаты специальной теории относительности
Лекция: специальная теория относительности и ее следствияПостулаты специальной теории
относительности
Эйнштейн предложил отказаться от поиска объяснений, почему
скорость света во всех ИСО оказывается одинаковой, и предложил
считать, что постоянство скорости света является фундаментальным
свойством природы, которое нужно констатировать как опытный факт.
В основу СТО Эйнштейн положил два постулата, или принципа, в
пользу которых говорит весь экспериментальный материал.
1. Принцип относительности. Все законы физики одинаковы во всех
инерциальных системах отсчёта, то есть имеют одинаковую форму и
значения констант, входящих в эти законы.
2. Принцип постоянства скорости света. Скорость света в вакууме
имеет одно и тоже значение, c 3 108 м / с,во всех ИСО, независимо от
скорости наблюдателя или скорости источника излучения света.
Первый постулат – обобщение механического принципа
относительности Галилея на все физические явления.
Всё содержание СТО вытекает из этих постулатов.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
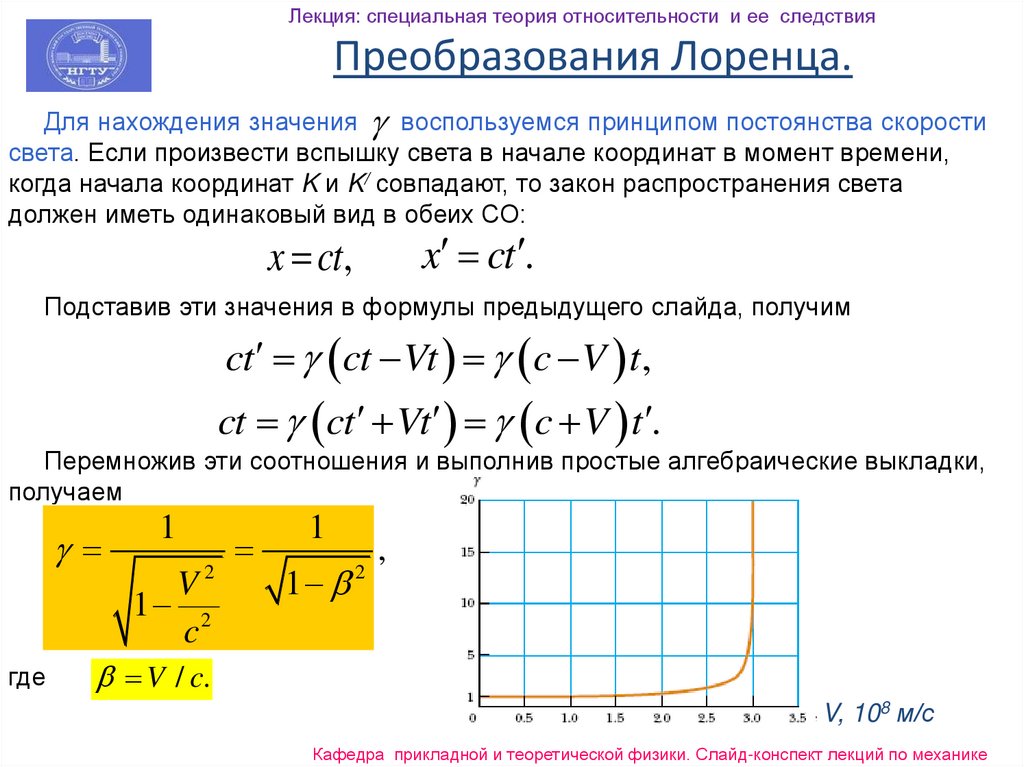
16. Преобразования Лоренца
Лекция: специальная теория относительности и ее следствияПреобразования Лоренца
Поскольку классический закон сложения скоростей, а значит и преобразования
Галилея, приводят к выводам противоречащим экспериментам, необходимы
новые преобразования. Они должны удовлетворять постулатам Эйнштейна и в
пределе малых скоростей (V<<c) переходить в преобразования Галилея. Эти
преобразования называются преобразованиями Лоренца.
Установим вид преобразований координат и
времени для частного случая тех же ИСО K и K/,
Y/
Y
которые были рассмотрены ранее: оси координат
K/
K
взаимно параллельны, скорость движения системы
P
K/ направлена вдоль оси 0x (см.Рис.), а в моменты
V
времени t =t /=0 начала координат 0 и 0/
0/
0
совпадают. Однако уже нельзя полагать, что t=t/ в
/
x
Vt
X
X / любой другой момент или в другом месте.
x
Из однородности пространства и времени следует,
Z
Z/
что формулы, связывающие координаты и время
систем отсчёта K и K/ должны быть линейными.
Поэтому разумно предположить, что
x x Vt , x x Vt , y y , z z
Константа должна быть функцией V и c, такой, что при V / c 1 она должна
приближаться к единице (
1 ). Часто называют лоренц-фактором.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
17. Преобразования Лоренца.
Лекция: специальная теория относительности и ее следствияПреобразования Лоренца.
Для нахождения значения воспользуемся принципом постоянства скорости
света. Если произвести вспышку света в начале координат в момент времени,
когда начала координат K и K/ совпадают, то закон распространения света
должен иметь одинаковый вид в обеих СО:
x ct .
x ct,
Подставив эти значения в формулы предыдущего слайда, получим
ct ct Vt c V t ,
ct ct Vt c V t .
Перемножив эти соотношения и выполнив простые алгебраические выкладки,
получаем
1
2
V
1 2
c
где
1
1
2
,
V / c.
V, 108 м/с
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
18. Преобразования Лоренца
Лекция: специальная теория относительности и ее следствияПреобразования Лоренца
Чтобы найти формулы преобразования времени, нужно воспользоваться
исходным преобразованием для x и x/ и разрешить его относительно t и t/.
В результате получаются правила перехода от координат и времени одной
ИСО к координатам и времени другой ИСО, которые называются
преобразованиями Лоренца для координат и времени.
K K
x Vt
x
,
1 2
K K
x
z z,
z z ,
1
y y ,
y y,
t V / c x
2
t
1
2
x Vt
.
t
2
,
t V / c 2 x
1 2
.
Слева – прямые преобразования. Справа – обратные преобразования Лоренца.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
19. Преобразования Лоренца
Лекция: специальная теория относительности и ее следствияПреобразования Лоренца
Из преобразований Лоренца следует, что:
• Между пространственными и временными координатами существует тесная
связь: не только пространственные координаты зависят от времени, но и время
зависит от пространственных координат (t = t/), а также от скорости движения
ИСО. Время не носит абсолютный характер, как это постулировалось в
классической механике Ньютона-Галилея. Время и пространство образуют
единое четырёхмерное пространство-время. Это связано с существованием
предельной скорости распространения взаимодействия.
• В пределе малых скоростей (V<<c) 1 и они переходят в преобразования
Галилея, то есть законы классической механики справедливы при скоростях
движения тел, много меньших предельной скорости c.
• При V>c выражения для x, t, x/ и t/ в преобразованиях Лоренца становятся
мнимыми. Это находится в соответствии с тем, что движение со скоростью V
большей предельной скорости c невозможно. Невозможна даже система отсчёта,
движущаяся со скоростью света, т.к. при V=c знаменатели в формулах для x и t
обращаются в нуль.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
20. Следствия из преобразований Лоренца
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца
1. Относительность понятия одновременности.
Пусть в системе K в точках с координатами x1 и x2 в одно и то же время
t1=t2=t (т.е. одновременно) происходят два события. Тогда, согласно
преобразованиям Лоренца, первое событие в системе K/ произойдёт в момент
времени
2
2
t1 x1 V / c t V / c
t1
,
2
2
1
1
А второе – в момент
t2
t2 x2 V / c 2
1
2
t x2 V / c 2
1
2
.
Как следует из этих формул,
t2 t1
x1 x2 V / c 2
1 2
0.
V / c.
Т.о., в системе K/ события оставаясь пространственно разобщёнными, оказываются и
неодновременными. Понятие одновременности является относительным.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
21. Следствия из преобразований Лоренца.
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца.
Пример иллюстрирующий относительность одновременности.
Вагон движется относительно Земли с постоянной скоростью. Расстояние
между точками на Земле AO=OB, а в вагоне A/O/=O/B/.
Пусть в момент времени, когда отмеченные на Земле и в вагоне точки
совпадают , в точки A и B ударят две молнии (Рис.a).
В силу того, что скорость света во всех ИСО одинакова и конечна (хоть и
велика), свет от обеих вспышек молний придёт в точку O одновременно, а в
точку O/ раньше придёт свет из B/, затем из A/. Следовательно событие в точке
B/ произошло раньше, чем в точке A/. Итак, понятие одновременности имеет
относительный смысл и в разных системах время течёт неодинаково.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
22. Следствия из преобразований Лоренца.
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца.
2. Размеры тел в разных системах отсчёта. Сокращение длины.
Y
Пусть в системе отсчёта K покоится линейка
(стержень) параллельная оси X (рис. слева). Её
длина в этой СО
L x x
Y
K K
Z
0
x1
Z
Отсюда
2
1
Найдём длину этой линейки L в движущейся
системе K/. Для этого нужно найти координаты её
концов x2/ и x1/ в один и тот же момент времени t1/ = t2/
= t/. Из преобразований Лоренца следует
Lp
V
0
p
x2 X
X
x2
x2 Vt
, x1
x1 Vt
.
1 2
1 2
x2 x1
L
Lp x2 x1
. Здесь V / c.
1 2
1 2
И искомая длина
L Lp 1 2 Lp .
(!!)
K
K
Если линейка покоится в системе K/ (рис. справа),то её длина в Kсистеме опять-таки определяется выражением (!!). Длина линейки
в той СО, где она покоится, называется собственной длиной L p .
Поперечные размеры тел (вдоль осей Y и Z) при движении вдоль
оси X не меняются. Т.о. линейные размеры тела наибольшие в
той СО, относительно которой оно покоится.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
23. Следствия из преобразований Лоренца.
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца.
3. Промежутки времени между событиями. Замедление времени.
Пусть в системе отсчёта K/, движущейся относительно системы K, в точке с
координатами x/, y/,z/ покоятся часы и происходят два последовательных события
(например, рождение и распад частицы) в моменты времени t1/ и t2/. Тогда
промежуток времени между этими событиями есть
t2 t1 .
Найдём промежуток времени между этими же событиями в системе K. Из
преобразований Лоренца, с учётом того, что события в системе K/ одноместные
(x1/ = x2/) имеем
t2
Откуда
t2 V / c 2 x
1
t
2
t1
,
1
2
.
t1 V / c 2 x
1
2
.
Время измеренное по часам,
движущимся вместе с телом,
называется собственным временем.
Таким образом, промежуток времени между двумя событиями, происходящими
в некоторой точке, наименьший в той ИСО, где эта точка неподвижна.
Иными словами, движущиеся часы идут медленнее покоящихся! t.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
24. Следствия из преобразований Лоренца
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца
Экспериментальное подтверждение эффекта замедления времени.
мюон
2 10 6 c
t 10 4 c
~30 км
Под действием космического излучения в
верхних слоях атмосферы на высоте 20 – 30 км
рождаются нестабильные частицы - мюоны.
Собственное время жизни мюонов (по часам
6
движущимся вместе с ними) 2 10 c . Если
бы время жизни мюонов не зависело от их
скорости, то двигаясь даже со скоростью света,
они проходили бы путь не больше, чем
c 3 108 2 10 6 600 м
Однако, измерения показывают, что большая
часть мюонов достигает поверхности Земли. Это
объясняется тем, что мюоны движутся со
скоростями близкими к скорости света. Поэтому
время
их
жизни
отсчитанное
по
часам
неподвижным относительно Земли гораздо больше
( t 10 4 c) и оказывается достаточным, чтобы
достичь поверхности Земли.
Существуют и другие подтверждения реальности эффекта замедления времени.
Земля
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
25. Следствия из преобразований Лоренца
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца
4. Релятивистский закон сложения скоростей
Пусть точка движется со скоростью v относительно системы K, а относительно
системы K/ - cо скоростью v . Найдём связь между ними.
Проекции векторов этих скоростей на оси координат
В системе K:
и
В системе K/ :
dz
dy
dx
, v z
v x
, v y
dt
dt
dt
dx
dz
dy
vx
, vy
.
, vz
dt
dt
dt
Из преобразованиям Лоренца имеем
dx dx Vdt , dy dy , dz dz ,
Отсюда
dt dt V / c 2 dx .
dx
dx Vdt
1 2
1 2
dz
dy
dz
dy
,
.
,
2
dt dt V / c dx dt dt V / c 2 dx dt dt V / c 2 dx
v x V
vx
,
2
1 Vv x / c
vy
v y 1 2
1 Vv x / c
2
,
v z 1 2
vz
.
2
1 Vv x / c
Это и есть релятивистский закон сложения скоростей. Он переходит в классический
закон при V<<c. При v/x= c и v/y =v/z = 0 оказывается, что vx = c . Это ещё раз
подчёркивает, что скорость света – максимально возможная скорость.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
26. Следствия из преобразований Лоренца
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца
4. Релятивистский закон сложения скоростей
Пусть частица движется со скоростью v относительно системы K, а относительно
системы K/ - cо скоростью v . Найдём связь между ними.
Проекции векторов этих скоростей на оси координат:
В системе K:
и
в системе K/ :
dx
dz
dy
dz
dy
dx
vx
, vy
.
, vz
, v z
v x
, v y
dt
dt
dt
dt
dt
dt
Cогласно преобразованиям Лоренца
dx dx Vdt , dy dy , dz dz ,
Отсюда
dx
dx Vdt
,
2
dt dt V / c dx
dt dt V / c 2 dx .
dy 1 2
dy
,
2
dt dt V / c dx
dz 1 2
dz
.
2
dt dt V / c dx
Это и есть релятивистский закон сложения скоростей. Он
переходит в классический закон при V<<c. При v/x= c и v/y=
v/z = 0 оказывается, что vx = c . Это ещё раз подчёркивает,
что скорость света – максимально возможная скорость.
v x V
vx
.
2
1 Vv x / c
vy
v y 1 2
1 Vv x / c
2
.
v z 1 2
vz
.
2
1 Vv x / c
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
27. Инварианты преобразований Лоренца. Интервал
Лекция: специальная теория относительности и ее следствияИнварианты преобразований Лоренца.
Интервал
Как уже отмечалось, одной из важнейших величин, которая не зависит от
ИСО, является скорость света в вакууме - с.
• Другим важным инвариантом преобразований Лоренца является величина S12,
называемая интервалом между двумя событиями, квадрат которой
определяется выражением
2
2 2
2
S12 c t12 12
где
t2 t1 t12- промежуток времени между двумя событиями,
l x2 x1 y2 y1 z2 z1 - пространственное
2
12
2
2
2
расстояние между этими же двумя событиями.
В инвариантности интервала легко убедится, вычислив его непосредственно в K
и K/ системах, воспользовавшись преобразованиями Лоренца. Инвариантность
интервала свидетельствует о том, что, расстояния и промежутки времени между
событиями связаны друг с другом и время является равноправной координатой
четырёхмерного пространства-времени.
• Из независимости скорости света и интервала от ИСО следует, что
собственное время , тоже является инвариантом преобразований Лоренца.
Таким образом, скорость света с, интервал S12 и собственное время инварианты преобразований Лоренца.
Экспериментально установлено, что ещё одной важной инвариантной величиной
является масса частицы (тела).
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
28. Интервал. Типы интервалов
Лекция: специальная теория относительности и ее следствияИнтервал. Типы интервалов
В зависимости от соотношения между пространственной (l12 ) и
временной (ct12) компонентами в интервале различают три их типа:
1. Времениподобный, если S122 > 0, т.е. c t12
2 2
2
12
c 2t122 l122 0.
События разделённые времениподобным интервалом не могут быть
одновремнными ни в какой системе отсчёта, но всегда можно найти такую K/систему, в которой оба события происходят в одной точке (l12/= 0).
2. Пространственноподобный, если S122<0.
Для такого типа интервалов (l12>ct12) всегда можно найти такую K/- систему, в
которой оба события происходят одновременно (t12/=0), но ни в какой системе
эти события не могут быть пространственно совмещёнными.
3. Светоподобный, если S122=0. Такой интервал существует между
событиями, которые могут быть связаны сигналом, распространяющимся со
скоростью света.
Причинно связанные события могут быть разделены только
времениподобным или светоподобным интервалом.
Является ли интервал времениподобным, пространственноподобным или
светоподобным, не зависит от ИСО. Это есть инвариантное свойство самих
событий.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
29. Релятивистские импульс и энергия
Лекция: специальная теория относительности и ее следствияРелятивистские импульс и энергия
Согласно принципу относительности, законы сохранения, как и другие
законы природы, должны быть инвариантными по отношению к
преобразованиям Лоренца.
Оказывается, что выражение для импульса частицы,
обеспечивающее инвариантность закона сохранения импульса, имеет
вид
p
mv
1 v2 / c2
mv .
Классическое определение импульса в виде p=mv пригодно только при v<<c.
Закон сохранения энергии оказывается инвариантным, если выражение
для полной энергии свободной частицы имеет вид
E
mc 2
1 v2 / c2
mc ,
2
где
1
1 (v / c )
2
2
.
Неподвижная частица ( v 0 ) обладает энергией E0 mc 2 , которая называется
энергией покоя. Это внутренняя энергия частицы. Классическая механика её не
учитывает, считая, что при v 0 энергия покоящегося тела ровна нулю.
В релятивистской механике под полной энергией свободной частицы
подразумевается сумма её кинетической энергии W и энергии покоя:
E W E0 .
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
30. Соотношение между импульсом, энергией и массой релятивистской частицы.
Лекция: специальная теория относительности и ее следствияСоотношение между импульсом, энергией и
массой релятивистской частицы.
Энергия и импульс частицы имеют различные значения в различных СО.
Оказывается, однако, что есть величина - некоторая комбинация E и p, которая
является инвариантной. Эта величина есть E2 – p2c2. В этом легко убедится
подстановкой выражений для E и p из предыдущего слайда:
E 2 p 2c 2 m2c 4 2 m2c 2v 2 2
2
2
2
(
c
v
)
c
2 2
2 4
m c
m c .
2
2
(c v )
E p c m c .
2
2 2
2 4
(1)
3
E
2
pc
Скорость света и масса – инварианты.
1
Значит и выражение E2- p2c2 , действительно, инвариант и
имеет одно и то же значение во всех ИСО.
По форме это выражение напоминает теорему Пифагора,
2
поэтому связь между E, p и m удобно наглядно представить в
mc
виде прямоугольного треугольника (см. рис.).
При v=0 треугольник превращается в прямую и E = mc2. С ростом скорости
частицы (на рис. это позиции гипотенузы 1, 2 и 3 соответственно) растут её
импульс и энергия, но комбинация их, определяемая уравнением (1), остаётся
неизменной.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
31. Кинетическая энергия релятивистской частицы.
Лекция: специальная теория относительности и ее следствияКинетическая энергия релятивистской частицы.
Кинетическая энергия свободной релятивистской частицы равна
разности её полной энергии и энергии покоя:
W E E0
Через скорость частицы кинетическая энергия
частицы выражается следующим образом:
1
W mc ( 1) mc
1 , где v / c.
1 2
2
2
Другое эквивалентное выражение для кинетической
энергии получается, если выразить полную энергию
через импульс по формуле (1) предыдущего слайда :
W
p 2c 2 m 2c 4 mc 2 .
E
W
pc
mc 2
E0 mc 2
Наглядное геометрическое представление связи между импульсом p,
полной энергией E, энергии покоя E0 и кинетической энергией W
приведено на рисунке.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
32. Кинетическая энергия релятивистской частицы
Лекция: специальная теория относительности и ее следствияКинетическая энергия релятивистской
частицы
Выражения для релятивистской кинетической энергии предыдущего
слайда сильно отличаются от классического
mv 2
p2
W
.
2
2
2m
Оказывается, что при малых скоростях ( v c)
релятивистские выражения для кинетической
энергии переходят в классическое.
Действительно, при 1 можно принять, что
2
v2
2
1 1 1
1 2 .
2
2c
И тогда
W
mv 2
v2
mc 1 2 1
.
2
2c
2
W Релятивистский
случай
mc 2
Классический
случай
V
На рисунке показаны для сравнения графики зависимости релятивистской
и классической кинетических энергий от скорости. Видно, что их различие
особенно сильно в области скоростей сравнимых со скоростью света.
Скорости движений, с которыми мы имеем дело в повседневной жизни и в
технике, настолько малы по сравнению с c , что применительно к этим
движениям ньютоновскую механику можно считать практически строгой.
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
33. Взаимосвязь массы и энергии
Лекция: специальная теория относительности и ее следствияВзаимосвязь массы и энергии
В соответствии с формулами для полной энергии
E mc 2
и E
p 2c 2 m2c 4
тела (частицы) обладают энергией даже тогда, когда они неподвижны
относительно нас. Это - энергия покоя:
E0 mc 2 .
Здесь заключено утверждение об эквивалентности энергии покоя и массы.
Это знаменитый результат Эйнштейна: масса может служить мерой
содержащейся в ней энергии. Отсюда вытекает, что всякое изменение
массы тела m сопровождается изменением энергии покоя E0 , причём
эти изменения пропорциональны друг другу:
E0 mc 2 .
Это утверждение называют законом взаимосвязи массы и энергии покоя.
Важно усвоить, что это не означает возможность превращать энергию в
массу или наоборот. Энергия покоя и масса – это одно и то же,
разные названия одной и той же сущности.
Пример. Подсчитаем энергетический эквивалент 1 килограмма:
2
8 2
Это огромная энергия !
E0 mc 1 3 10 9 1016 Дж.
Такое количество энергии Днепрогэс вырабатывает за 8 лет!
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
34. Следствия из преобразований Лоренца
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца
4. Релятивистский закон преобразования и сложения скоростей
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
35. Следствия из преобразований Лоренца
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца
4. Релятивистский закон преобразования и сложения скоростей
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике
36. Следствия из преобразований Лоренца
Лекция: специальная теория относительности и ее следствияСледствия из преобразований Лоренца
4. Релятивистский закон преобразования и сложения скоростей
Кафедра прикладной и теоретической физики. Слайд-конспект лекций по механике


































 physics
physics








