Релятивистская динамика

1.

9.8 Релятивистская динамика
Принцип относительности Эйнштейна требует, чтобы все
законы природы имели один и тот же вид во всех инерциальных
системах отсчета. Этому принципу должны удовлетворять, в том
числе, законы сохранения импульса, энергии и 2-й закон динамики
Ньютона. Прежняя форма 2-го закона Ньютона
r r
dp
=F
dt
r
r
p = m0
где
не является релятивистски инвариантной, так как она меняет свой
вид при переходе из одной инерциальной системы отсчета в другую.
Для нахождения нового, релятивистски инвариантного
уравнения динамики воспользуемся свойством инвариантности
интервала между двумя событиями
s = c t x - y - z
2
2
2
2
2

2.

Это выражение дает “длину” 4-х мерного вектора в
пространстве Минковского в инерциальной системе отсчета К.
Компонентами этого вектора выступают три проекции на декартовы
оси и одна проекция на ось времени
x, y, z, c t
При переходе к новой инерциальной системе отсчета К´,
движущейся относительно К вдоль оси у со скоростью
компоненты меняются согласно преобразованиям Лоренца
Δx´ = Δx
Δz´ = Δz
y' =
y -V t
V
1-
c
2
V
эти
V y
t - 2
c
t' =
2
V
1-
c
При этом интервал (длина 4-х мерного вектора) не меняется Δs = Δs´

3.

Пусть некоторое физическое свойство описывается 4-х
мерным вектором с компонентами на 4-е оси системы
r
A = (Ax , Ay , Az , At )
где
Аt –
К
аналог
сΔt
Потребуем, чтобы при переходе к новой системе координат
К´y
V
A
A
компоненты
этого
вектора
преобразовывались
также
как
и
разности
A
V
A
t
2
'
'
y
t
'
'
c
A = A xдвух
; Aточек
= Ay ; A =
координат
A =
2
y'
x'
y'
2
t'
V
1-
c
r
A
A - A - A A = A - A
Тогда2“длина”2 вектора2
t
x
y
V
1-
c
A
2
2
2 и интервал
2
будет
инвариантом,
как
'
'
'
'
z
t'
x'
- A
y'
z'
2

4.

Любой физический закон выражает связь между физическими
величинами. Пусть, например, закон связывает две физические
величины А и В, которые в инерциальной системе
К
изображаются 4-х мерными векторами в пространстве Минковского
r
r
A = (Ax , Ay , Az , At ) ; B = (B x , B y , Bz , Bt )
Тогда релятивистски инвариантный закон можно записать в
виде равенства этих векторов, поскольку преобразования двух
векторов при переходе к новой инерциальной системе отсчета К´
происходят по одинаковым формулам и значит равенство этих
векторов, то есть физический закон, не будет менять свою форму
в компонентах
r r
r
r
A = B ; A' = B'
Ax Bx ; Ay B y ; Az Bz ; At Bt
A' x B' x ; A' y B' y ; A' z B' z ; A't B't

5.

Для нахождения релятивистского выражения r импульса
рассмотрим частицу, которая движется со скоростью
относительно неподвижной инерциальной системы К. Пусть за
время
r
dr
dt
частица переместилась на вектор
.
Составим 4-х мерный вектор с компонентами
r
(dr, cdt)
Если умножить этот вектор на некоторую постоянную, то получим
снова 4-х мерный вектор. Выберем в качестве такой постоянной
m0 /dt0
где
m0 – некоторая константа,
2
υ
dt0 dt 1 -
c
– собственное время, в системе отсчета,
связанной с частицей.

6.

В результате умножения получим новый 4-х мерный вектор с
компонентами
m0 r
(dr, cdt) =
dt0
m0
2
υ
dt 1 -
c
r
(dr, cdt) =
(9.8.1)
r
r
r
m0
dr
m0
=
( , c) =
( , c) = m( , c)
2
2
dt
υ
υ
1-
1-
c
c

7.

Здесь введено обозначение
m
m0
2
υ
1-
c
Если частица движется медленно, так что
(9.8.2)
υ/c <<1,
m ≈ m0 , то пространственная составляющая
4-х мерного вектора
r
нерелятивистской частицы (m0 , m0 c) будет равна импульсу в
ньютоновской механике
r
r
p = m0
если m0 отождествить с массой частицы в нерелятивистской
механике. Ее называют массой покоя - это масса частицы в системе,
относительно которой частица находится в состоянии покоя.
В релятивистской механике вектор
импульса вводится по
r
r
аналогии согласно
P=m
(9.8.3)
m – релятивистская масса

8.

Применение формулы (9.8.3) к системе тел, в частности к
удару двух шаров показывает, что суммарный импульс системы
сохраняется.
Вектор импульса можно записать в другом виде
r
r
r
dr
P = m m
dt
где
dt0
r
m0 dr
r
dr
m0
2
dt
0
dt 1 -
c
(9.8.4)
- собственное время.
Эксперименты на ускорителях элементарных частиц
подтверждают, что релятивистский импульс, определенный
формулами (9.8.3-9.8.4), сохраняется во всех процессах
столкновений.
При приближении скорости частицы к скорости света
c
релятивистская масса частицы m неограниченно
растет.

9.

Подставим релятивистский импульс во 2-ой закон Ньютона,
получим основной закон релятивистской динамики материальной
точки
r
r
r dp d m0
F=
=
(9.8.5)
2
dt dt
1-
r c
r
r
r d
m0
d
m0
=
3/2
2 dt
2
dt
2
1-
c
1 -
c
r c
r
r r
ma m(a
)
2
2
c
1 -
c

10.

Из него следует, что ускорение точки
r
r d
a=
dt
в общем случае не совпадает с направлением силы.
Значит, сопротивление тела движущей силе
зависит от угла между силой и скоростью.
Поэтому в релятивистской механике масса тела
перестает играть роль меры инертности тела.

11.

9.9 Взаимосвязь массы и энергии
Найдем кинетическую энергию релятивистской
частицы. Для этого используем то, что элементарная работа
на малом перемещении равна приращению кинетической
энергии
r
r r
rr
rr
dP r
dT = dA = (Fdr) = (F )dt = ( )dt = (dP ) =
dt
r
r r
2 r r
m0 ( d )
r m0 ( d )
= m0
d
=
2
2
2 3/2
2
1-
1
1 -
c
c
c
c

12.

Учитывая, что
получаем
r r
2
( d ) = d(
)
2
после преобразований
2
m0 c
dT = d
2
1-
c
Интегрируя, находим кинетическую энергию
T=
m0 c
2
2
1-
c
const

13.

Константу интегрирования найдем из условия,
кинетическая энергия покоящейся частицы равна нулю.
Полагаем
2
что
0 = m0 c const
2
const m0 c
Поэтому кинетическая энергия релятивистской частицы равна
T=
m0 c
2
2
m0 c
1-
c
скоростей
=c
Для малых
выражение для кинетической энергии
2
получаем нерелятивистское
m0
T = m0 c (1 + 2 + .... - 1)
2c
2
2
2
(9.9.1)
2

14.

Энергия
E 0 = m0 c
2
называется энергией покоя.
Энергия покоя является внутренней энергией тела, она не
связана с его движением как целого. Если тело состоит из многих
частиц, то энергия покоя равна сумме энергий покоя этих частиц, их
кинетических энергий движения относительно центра масс и
потенциальной энергии взаимодействия друг с другом.
Сумма кинетической энергии и энергии покоя дает
полную энергию свободной частицы
E = T + E0 =
m0 c 2
2
1-
c
mc
2
(9.9.2)
Эта формула выражает собой взаимосвязь между массой тела и
его энергией. Она показывает, что всякое изменение массы тела
приводит к изменению его энергии.

15.

В полную энергию свободной частицы Е не входит
потенциальная энергия тела во внешнем поле.
Используя выражение для релятивистский импульса, выразим
полную энергию свободной частицы через импульс
m0
P =
2
1- 2
c
2
2
m c
E =
1- 2
c
2
;
Отсюда находим релятивистское
энергией и импульсом частицы
2 4
0
2
соотношение
между
E =m c P c
или
2
2 4
0
2
E=c m c P
2
0
2
полной
2
2
(9.9.3)

16.

9.10 Законы преобразований релятивистского
и энергии
Пусть, как и раньше, система
К
импульса
неподвижная, а система
К
´движется относительно нее со скоростью V вдоль оси y.
Пусть частица в системе К за малое время dt переместилась
r
на малый вектор dr с проекциями на декартовые оси dx, dy, dz.
Согласно преобразованиям Лоренца в системе К´частица за
r
время dt´переместится на вектор dr' с проекциями dx´, dy´, dz´
dx´ = dx
dz´ = dz
dy' =
dy -Vdt
2
V
1-
c
Vdy
dt - 2
c
dt' =
2
V
1-
c

17.

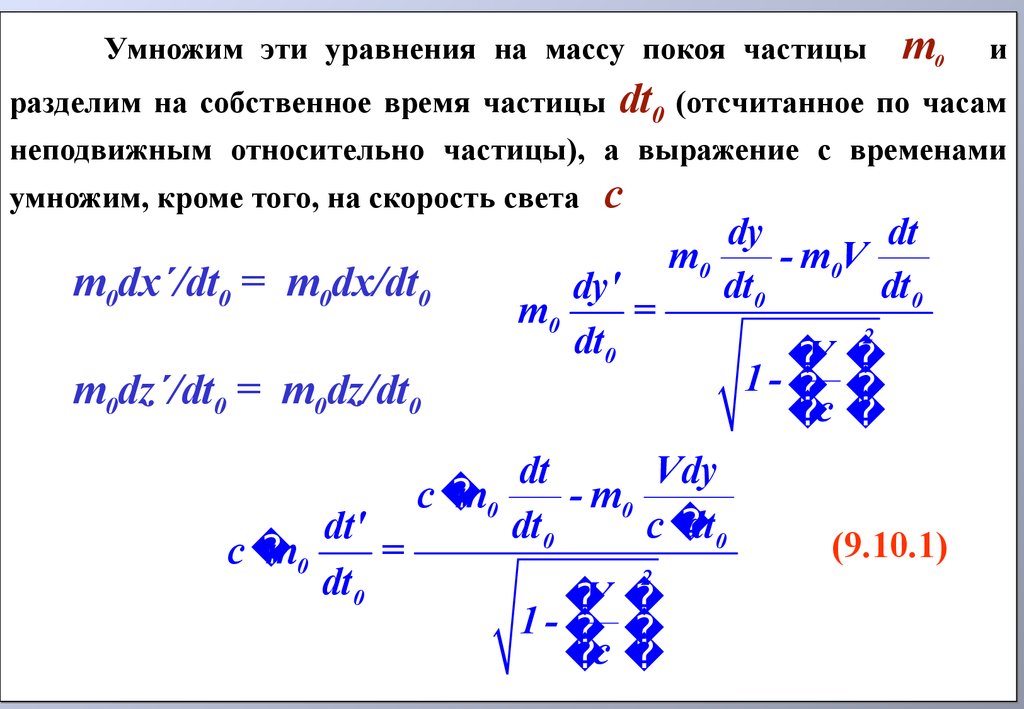
Умножим эти уравнения на массу покоя частицы
m0
и
разделим на собственное время частицы dt0 (отсчитанное по часам
неподвижным относительно частицы), а выражение с временами
умножим, кроме того, на скорость света
m0dx´/dt0 = m0dx/dt0
m0dz´/dt0 = m0dz/dt0
dt'
c
m0
=
dt0
с
dy'
m0
=
dt0
dy
dt
m0
- m0V
dt0
dt0
dt
Vdy
c
m0
- m0
dt0
c
dt0
2
V
1-
c
2
V
1-
c
(9.10.1)

18.

r
r
dr
P = m0
dt0
Учтем, что согласно (9.8.3)
Или в компонентах
dx
Px = m0
dt0
dy
; Py = m0
dt0
dx'
P = m0
dt0
dy'
; P = m0
dt0
'
x
Так как dx´ = dx
то
'
y
r
r
dr'
; P' = m0
dt0
;
dz
Pz = m0
dt0
;
dz'
P = m0
dt0
'
z
dz´ = dz
'
x
Px = P
'
z
; Pz = P

19.

Поскольку
2
υ
dt0 dt 1 -
c
то полную энергию частицы в системе
dt
E = mc =
= m0 c
2
dt
0
υ
1-
c
2
m0 c
2
K
2
можно записать в виде
dt
E
2
dt0 m0 c
Аналогично полная энергия частицы в системе
dt'
E' = m0 c
dt0
2
K´ равна
dt'
E'
dt0 m0 c 2

20.

Тогда формулу, связывающую проекции импульсов на ось
двух системах отсчета можно переписать в виде
dy'
P = m0
=
dt0
'
y
dy
dt
m0
- m0V
dt0
dt0
2
V
1-
c
E
Py - m0V
m0 c 2
2
V
1-
c
yв
E
Py -V 2
c
2
V
1-
c

21.

Теперь из формулы (9.10.1), связывающей времена в двух
системах отсчета, получим формулу, связывающую полные энергии
частицы в этих системах
dt'
E'
E'
c
m0
c
m0
=
=
2
dt0
m0 c
c
VPy
E
c
m0
2
m0 c
c
2
V
1-
c
dt
Vdy
c
m0
- m0
dt0
c
dt0
2
V
1-
c
E VPy
c
c
2
V
1-
c

22.

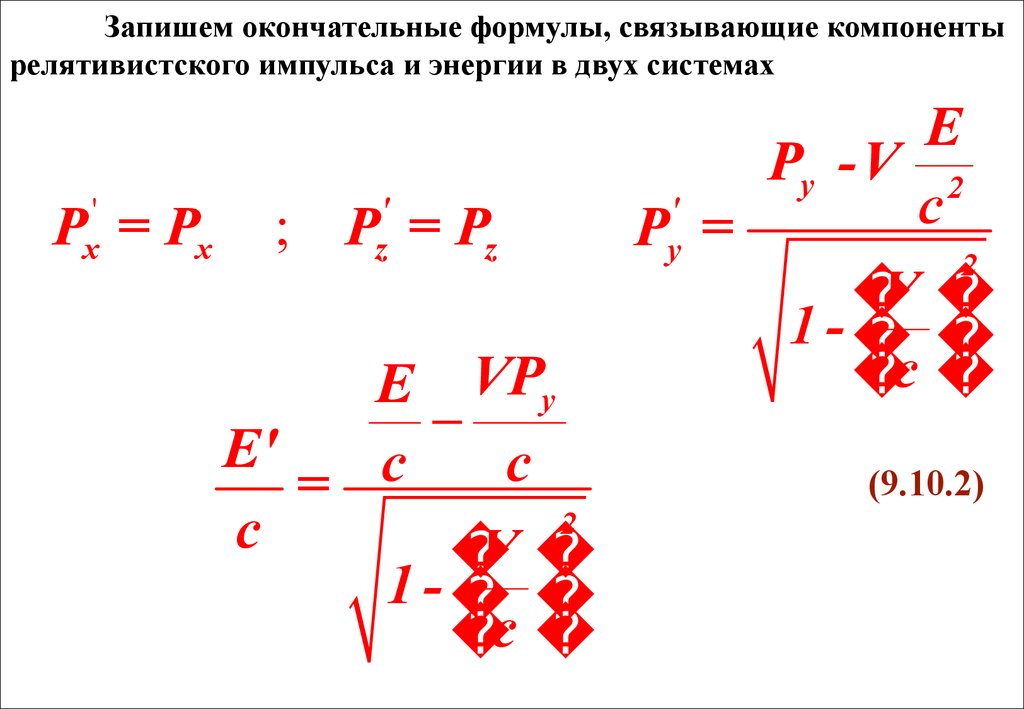
Запишем окончательные формулы, связывающие компоненты
релятивистского импульса и энергии в двух системах
'
x
P = Px
'
z
; P = Pz
E VPy
E'
c
c
=
2
c
V
1-
c
E
Py -V 2
'
c
Py =
2
V
1-
c
(9.10.2)

23.

Из формул (9.10.2) и результатов параграфа (9.8) следует, что
совокупность величин
Px
; Py
; Pz
;
E
c
r E
( P, )
c
образует 4-х мерный вектор - вектор энергии-импульса.
Сравнивая с прежней формулой (9.8.1) для 4-х мерного вектора
r
m( , c)
видим, что они совпадают, так как
r
r
P = m
E
mc
c
Из (9.9.3), следует, что “длина” вектора энергии-импульса
является инвариантом движения
2
2
2
2
2
(9.10.3)
x
y
z
0
E
P P P m c
c

24.

9.11
Энергия связи системы
Пусть покоящееся тело с массой покоя
М0
состоит из
N
частей с массами покоя m0i. Энергия покоя такого тела слагается из
энергий покоя ее частей, кинетических энергий этих частей и
потенциальной энергии взаимодействия их друг с другом.
Поэтому энергия покоя составного тела больше суммы
N
энергий покоя его частей
2
2
M 0 c > m0i c
i=1
Следовательно, масса составного тела больше суммы масс его
частей. Значит, масса взаимодействующих частиц теряет свойство
аддитивности.
При распаде составного тела N на части энергия, равная
2
2
разности
M 0 c - m0i c
i=1

25.

При обратном процессе - неупругом соударении частиц они
сливаются в одно целое, а их кинетическая энергия переходит в
эквивалентное количество энергии покоя составного тела. Поэтому
масса образовавшегося тела больше суммы масс исходных частиц
N
на величину
M = M 0 m0i
i=1
Составное тело не будет распадаться на части, если его
энергия покоя меньше суммы энергий покоя частей
2
M0 c <
N
m
0i
c
2
i=1
Чтобы разложить такое тело на составные части и разорвать
связи между ними, необходимо затратить энергию, равную энергии
связи
N
Eсвязи = m0i c - M 0 c
2
i=1
2

26.

Энергия связи равна работе, которую надо затратить, чтобы
разложить систему на составные части.
При слиянии частиц энергия связи выделяется.
235
Например, цепная реакция деления ядер урана U 92 при
захвате медленных нейтронов идет одним из возможных способов
согласно
U
235
92
n U
236
92
Cs
140
55
Rb 2n
94
37
235
Сумма масс урана U 92
и нейтрона больше суммы масс
распавшихся частиц на величину m = 4 10-29 кг.
Этому избытку массы отвечает большая энергия
2
-11
ΔE = Δm
c = 4
10Дж = 250 Мэв
которая превращается в кинетическую энергию осколков деления
и энергию фотонов.

27.

При синтезе легких ядер выделяется еще большая энергия.
Например, при слиянии ядер тяжелого водорода
3
дейтерия H 12 или трития H 1 , выделяется энергия
H H H pМэВ 4
2
1
2
1
3
1
H H H nМэВ17.6
2
1
3
1
4
2
Однако, чтобы соединить эти ядра надо сблизить их до расстояния
~ 2 pm = 2·10-15 м
равного радиусу действия ядерных сил. Для этого надо совершить
работу, равную потенциальной энергии отталкивания заряженных
частей
0.35 МэВ

28.

9.12
Частицы с нулевой массой
Рассмотрим частицу, которая движется со скоростью, равной
скорости света υ = c. Согласно релятивистским формулам
E=
m0 c
2
2
1-
c
r
P=
r
m0
2
1-
c
чтобы энергия и импульс были конечными такая частица должна
иметь массу покоя, равную нулю m0 = 0. Тогда из формулы
E = m02 c 4 P 2 c 2
следует
E = Pc
E
P=
c
(9.12.1)

29.

Энергия фотона дается формулой Планка
E = hν
где
h
– постоянная Планка, равная 6.62 10-34 Дж сек ,
- частота света.
Подставляя
импульса фотона
в
(9.12.1), получаем выражение для
h
p=
c

30.

9.13
Давление света
Свет представляет собой поток корпускул - фотонов. При
поглощении света поверхности тела передается импульс, равный
сумме импульсов поглощенных фотонов, что приводит к
возникновению давления, оказываемого светом на тело.
Найдем давление света.
Пусть на единицу площади поверхности 1 м2 за 1 сек падает
и ею поглощается N фотонов. В результате этой площади передается
энергия ( плотность потока энергии )
W = Nhν
и импульс
h
W
pN = N
c
c
Поскольку импульс, передан в единицу времени, то он равен
силе, а так как сила отнесена к единице площади, то она равна
давлению, испытываемому телом
W
P
c
Впервые световое давление в 1899 г. измерил Лебедев.