Прямые общего и частного положения

1. Прямые

общего и частного
положения

2.

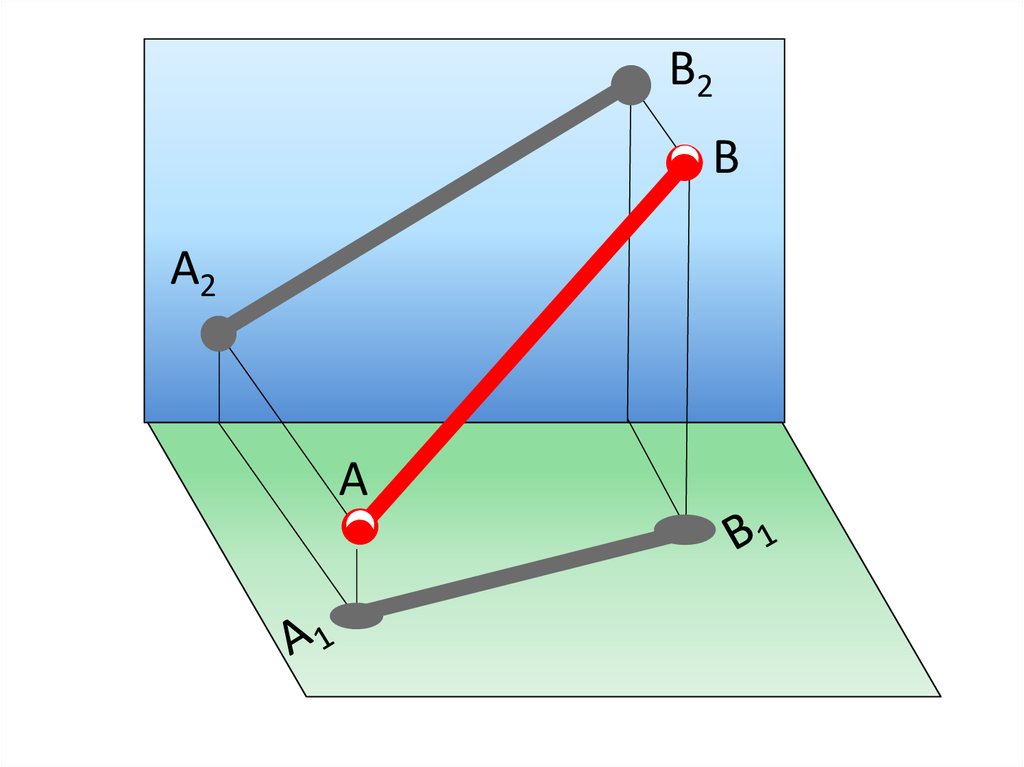
В2
В
А2
А

3.

В2
В2
В
n2
А2
А2
А
х12
А1
n1
В1
Прямая, не параллельная и не
перпендикулярная ни одной из плоскостей
проекций, называется
прямой ОБЩЕГО положения

4.

Прямые,
параллельные
или
перпендикулярные плоскостям проекций,
называются
прямыми
ЧАСТНОГО
положения.

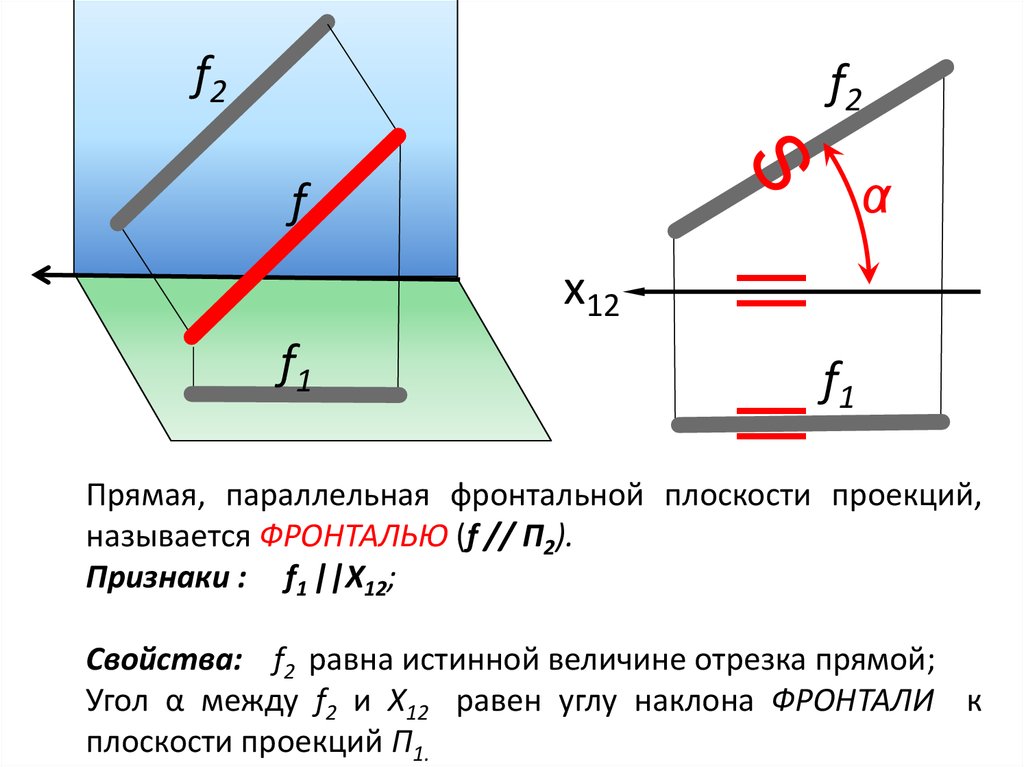
5.

f2
f2
f
х12
f1
α
f1
Прямая, параллельная фронтальной плоскости проекций,
называется ФРОНТАЛЬЮ (f // П2).
Признаки : f1 ||Х12;
Свойства: f2 равна истинной величине отрезка прямой;
Угол α между f2 и X12 равен углу наклона ФРОНТАЛИ к
плоскости проекций П1.

6.

h2
h2
h
х12
β
h1
h1
Прямая, параллельная горизонтальной плоскости проекций,
называется ГОРИЗОНТАЛЬЮ (h || П1).
Признаки : h2 || Х12.
Свойства: h1 равна истинной величине отрезка прямой;
угол β между h1 и X12 равен углу наклона ГОРИЗОНТАЛИ к
плоскости проекций П2.

7.

z
z
p2
П2
β
p2
p
p3
x12
П3
y
90
p3
α
90
p1
y1
Прямая, параллельная профильной плоскости проекций П3,
называется ПРОФИЛЬНОЙ ПРЯМОЙ (р || П3).
Признаки : р1 Х12 , р2 Х12 .
Свойства: р3 равна истинной величине отрезка прямой;
углы и β есть углы наклона профильной прямой к
плоскостям проекций П1 и П2 соответственно.
y3

8.

Прямые, перпендикулярные плоскостям
проекций П1 , П2 или П3, называются
горизонтально ПРОЕЦИРУЮЩИМИ ( П1),
фронтально ПРОЕЦИРУЮЩИМИ ( П2), или
профильно ПРОЕЦИРУЮЩИМИ ( П3)
соответственно.

9.

a2
S
a2
a
x12
x12
90
a1
Горизонтально проецирующая прямая (а П1).
Признаки: горизонтальная проекция а1 – ТОЧКА;
фронтальная проекция а2 х12.
Свойства: фронтальная проекция а2 - ИСТИННАЯ
ВЕЛИЧИНА отрезка прямой.

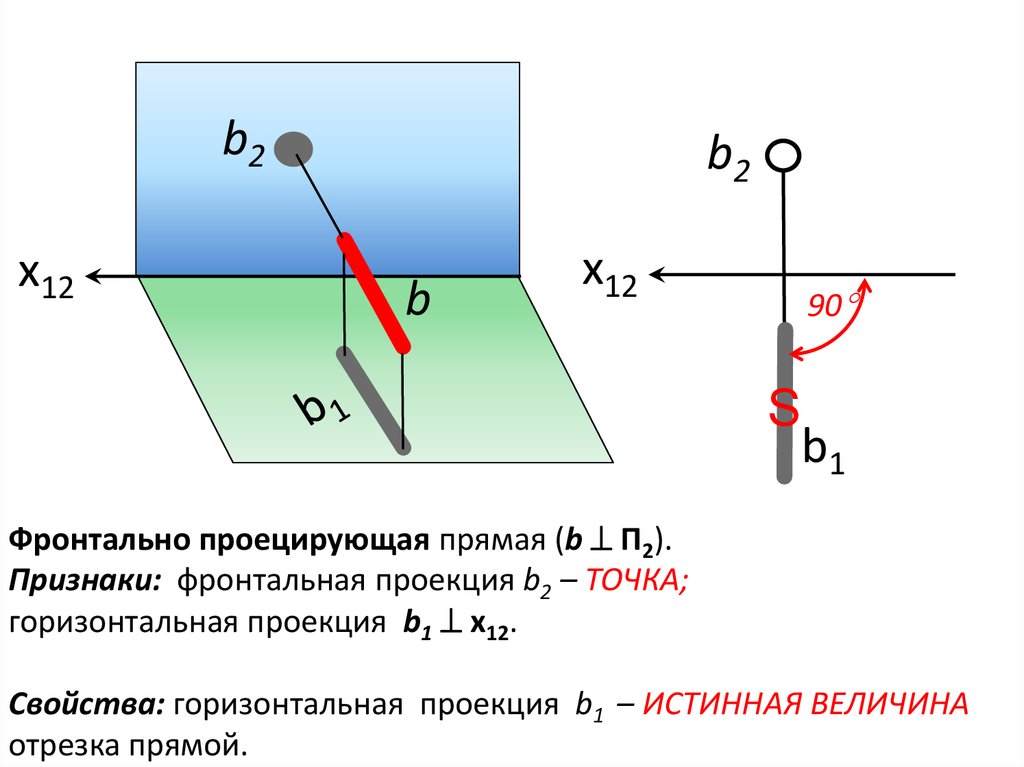
10.

b2
x12
b2
b
x12
90
S
b1
Фронтально проецирующая прямая (b П2).
Признаки: фронтальная проекция b2 – ТОЧКА;
горизонтальная проекция b1 х12.
Свойства: горизонтальная проекция b1 – ИСТИННАЯ ВЕЛИЧИНА
отрезка прямой.

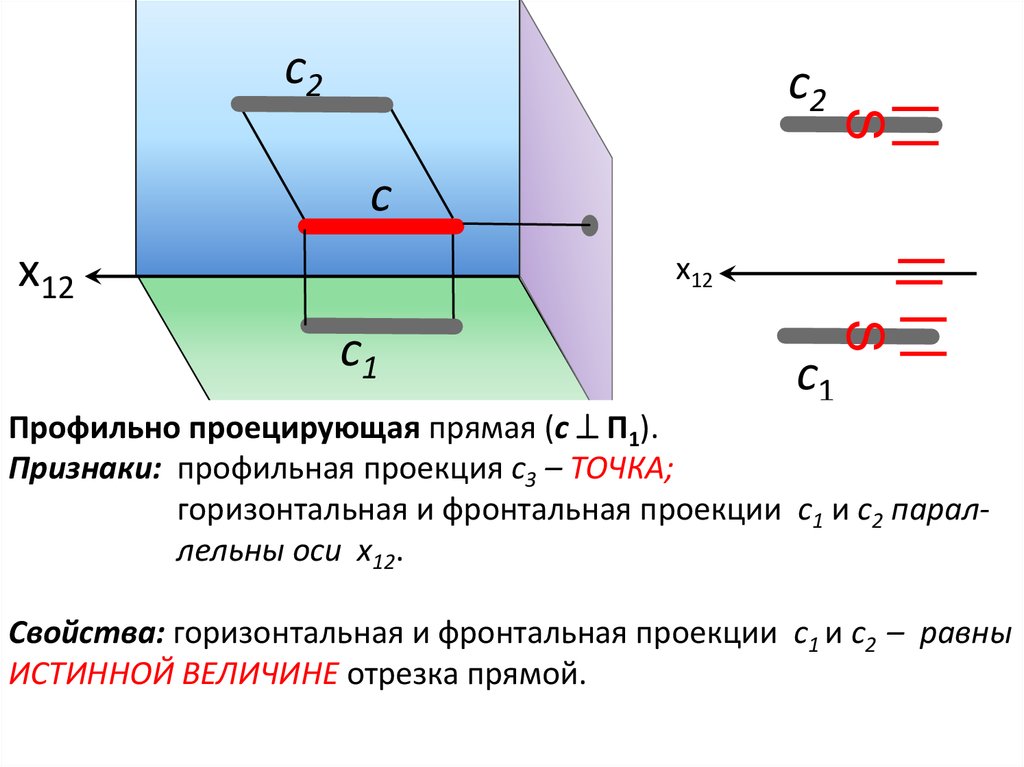
11.

c2
S
c2
c
x12
x12
c1
S
c1
Профильно проецирующая прямая (c П1).
Признаки: профильная проекция c3 – ТОЧКА;
горизонтальная и фронтальная проекции c1 и c2 параллельны оси х12.
Свойства: горизонтальная и фронтальная проекции c1 и c2 – равны
ИСТИННОЙ ВЕЛИЧИНЕ отрезка прямой.

12. Принадлежность точки прямой

13.

K2
K2
K
m2
х12
K1
m1
K1

14.

15.

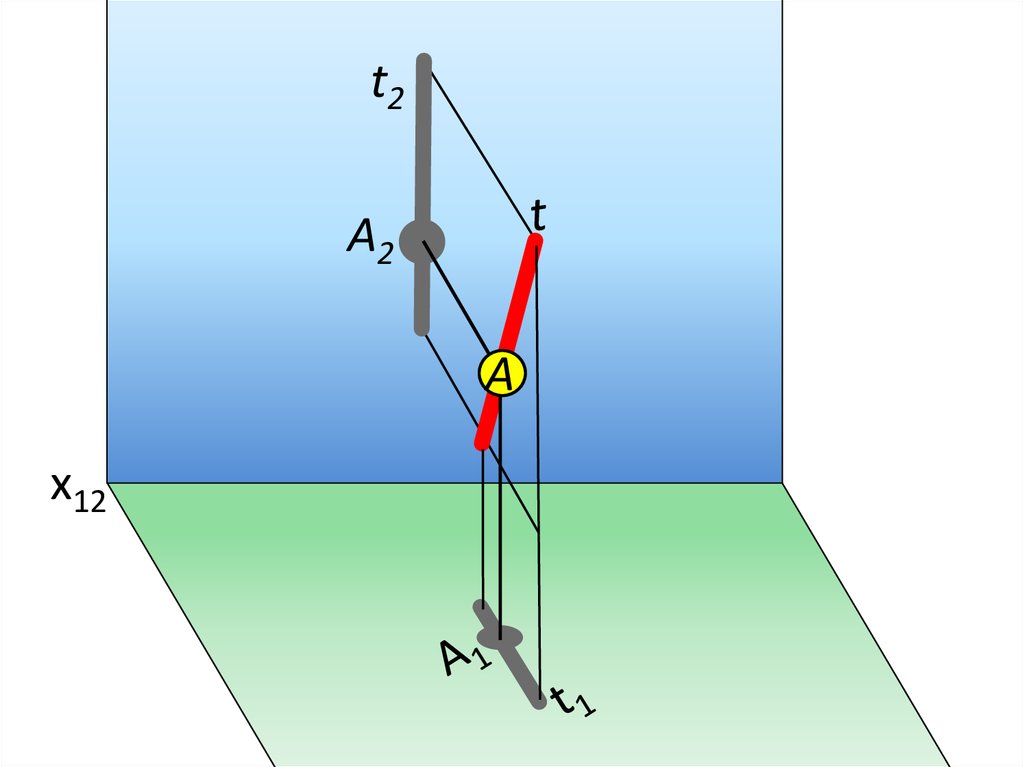
t2
A2
A
x12

16.

F2
A2
Е2
x12
Е1
????
F1

17.

F2
S2
F0
A2
Е2
Е0
A0
x12
Е1
A1
F1
S1

18.

Взаимное положение прямых

19.

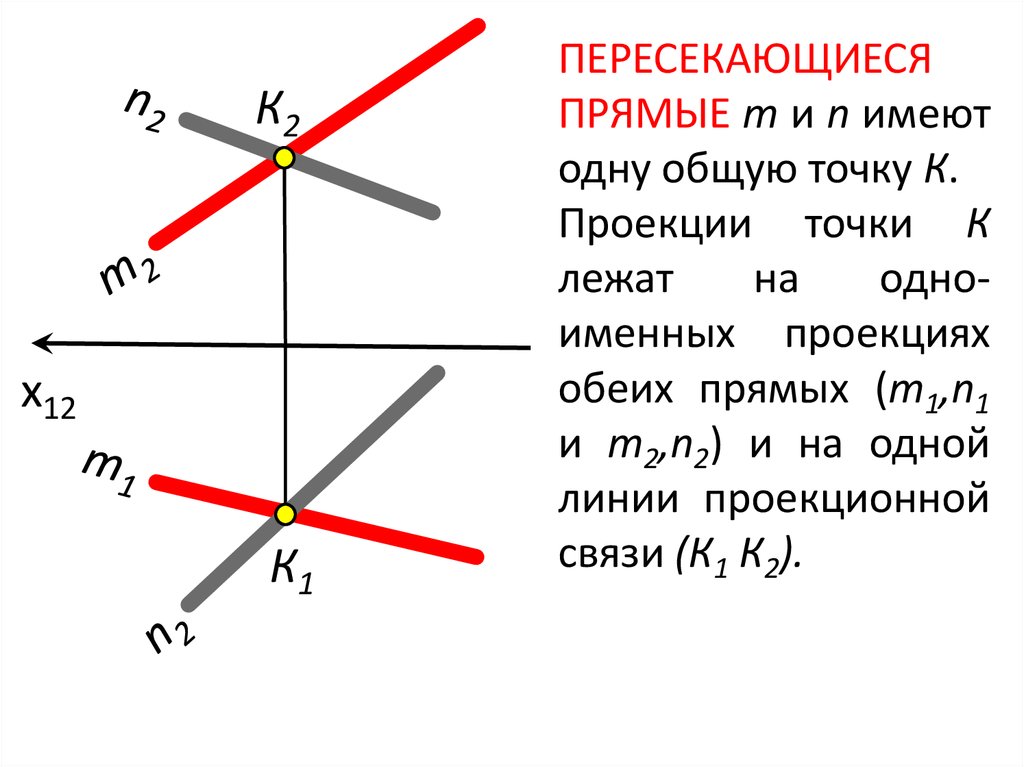
К2
x12
К1
ПЕРЕСЕКАЮЩИЕСЯ
ПРЯМЫЕ m и n имеют
одну общую точку К.
Проекции точки К
лежат
на
одноименных проекциях
обеих прямых (m1,n1
и m2,n2) и на одной
линии проекционной
связи (К1 К2).

20.

s2
x12
s1
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ а и b, а также t и s
имеют параллельные одноименные проекции:
a1 || b1 ; a2 || b2 и t2 || s2 .

21.

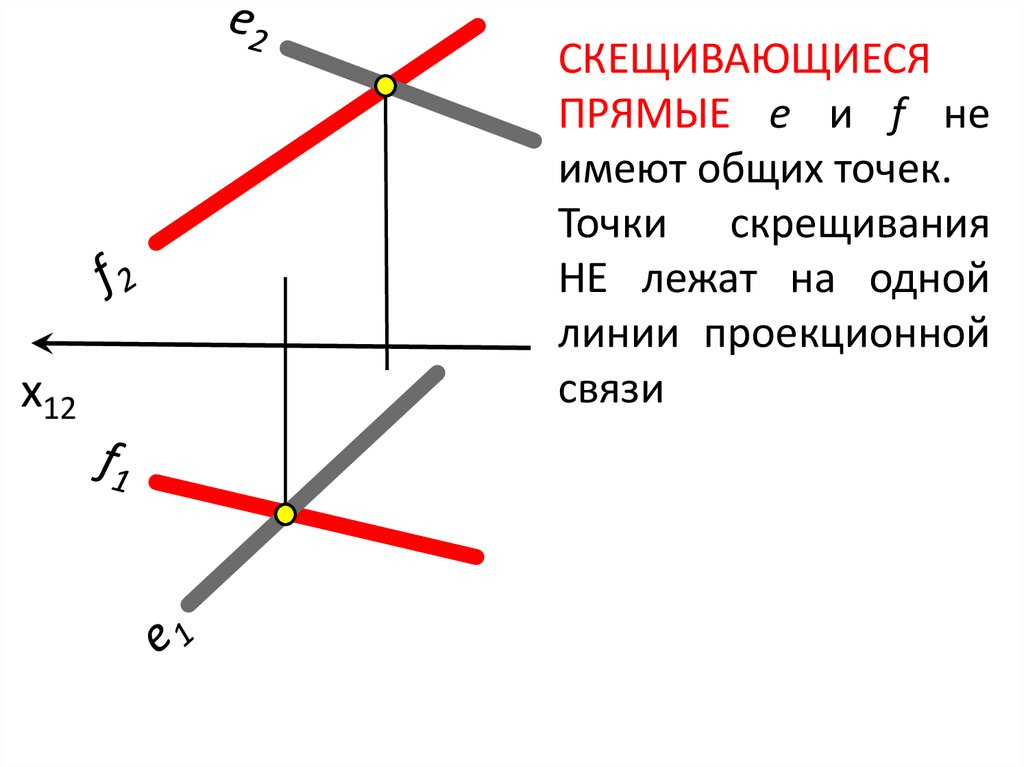
x12
СКЕЩИВАЮЩИЕСЯ
ПРЯМЫЕ e и f не
имеют общих точек.
Точки скрещивания
НЕ лежат на одной
линии проекционной
связи

22. Видимость скрещивающихся прямых

23.

12 (2
222)
x12
21
11

24.

42
x12
12 (22)
32
21
31
(3
) 4411
11

25.

Если один из катетов прямого угла
параллелен одной из плоскостей
проекций, то на эту плоскость
проекций угол проецируется в
истинную величину (90 ).

26.

С2
А2
В = 90 ;
АВ || П1.
h2
В2
х12
h1
В пространстве:
На чертеже :
В1
А2В2 (h2) || х12;
на П1 В1 = 90
А1
С1