Similar presentations:
Analýza časových řad
1. Analýza časových řad
2. Analýza časových řad Časová řada - množina pozorování kvantitativní charakteristiky (ukazatele), uspořádaná v čase. Členění
Analýza časových řadČasová řada - množina pozorování kvantitativní charakteristiky (ukazatele),
uspořádaná v čase.
Členění časových řad:
a) Podle rozhodného časového hlediska
Časová řada okamžiková
Časová řada intervalová
b) podle periodicity sledování
Časová řada krátkodobá (periodicita ukazatele je kratší než 1
rok)
Časová řada dlouhodobá (periodicita ukazatelů je nejméně
roční).
3.
c) podle druhu sledovaných ukazatelůČasová řada původních hodnot
Časová řada odvozených ukazatelů
d) podle způsobu vyjádření údajů
Časová řada naturálních ukazatelů
Časová řada peněžních ukazatelů
4. Základní charakteristiky časových řad 1) Posouzení úrovně časové řady - průměry
Základní charakteristiky časových řad1) Posouzení úrovně časové řady - průměry
Pracujeme-li s intervalovou časovou řadou, určuje se průměr
jako průměr aritmetický. Jsou-li všechny intervaly stejně
dlouhé, určí se prostý aritmetický průměr, při nestejně
dlouhých intervalech je nutno počítat vážený aritmetický
průměr.
Příklad
Časová řada vývoje výše průměrných mezd
Rok 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010
Kč
14478 15550 16457 17595 18283 19447 20923 22653 23426 23949
ti
yi
1
2
3
4
5
6
7
8
9
10
14478 15550 16457 17595 18283 19447 20923 22653 23426 23949
y
yi
= 192761 = 19276,1
n
10
5. V případě práce s údaji okamžikovými musíme užít průměr chronologický
V případě práce s údaji okamžikovými musíme užítprůměr chronologický
y
1 y y ....... y yn
n 1 2
Průměr chronologický : y 2 2 3
n 1
Prostá forma chronologického průměru je použitelná v případech, kdy
intervaly mezi jednotlivými okamžiky příslušné okamžikové řady
časové jsou stejně dlouhé.
6.
Pokud jsou tyto intervaly nestejně dlouhé, musí se užívat váženýchronologický průměr:
y y
y yn
y y
2
3
n
1
1
2
(
t
t
)
(
t
t
)
(tn t )
2 1
3 2
n 1
2
2
y 2
tn t
1
7. Příklad
Počet zaměstnanců v určitém podniku1.1.
1.2.
1.3.
1.4.
1.5.
26
28
25
30
28
za měsíc leden :
za měsíc únor :
za měsíc březen :
za měsíc duben :
(26+28)/2
(28+25)/2
( 25+30)/2
(30+28)/2
Chronologický průměr :
y
1 y y ....... y yn
2 3
n 1 2 = 13 28 25 30 14 = 27,5
y 2
n 1
4
8. 2) Posouzení dynamiky vývoje časových řad
Absolutní charakteristikyPrvní absolutní diference (absolutní přírůstky)
dyt = yt - yt-1,
t = 2, 3, . . ., n.
Druhá absolutní diference :
d(2)yt = dyt - dyt-1
Druhé absolutní diference charakterizují absolutní zrychlení, respektive
zpomalení vývoje ve zkoumané časové řadě, udávají, o kolik byl
následující přírůstek větší, respektive menší než předcházející.
Analogicky lze stanovit absolutní diference vyšších stupňů (třetího,
čtvrtého atd.), jejichž řady se vždy postupně zkracují o jeden člen.
9.
Relativní charakteristikyPrvní relativní diference - koeficienty růstu
yt
kt
y
t 1
které charakterizují relativní postupnou rychlost změn hodnot v časové
řadě. Vyjádříme-li koeficient růstu v procentech, hovoříme o tempu
růstu.
Za celou časovou řadu lze určit průměrný koeficient růstu k ,
definovaný nejčastěji jako geometrický průměr jednotlivých
koeficientů kt:
y
k n 1 2
y
1
y
3 yn n 1
y
y
2
n 1
yn
y
1
V případě, že první hodnota řady je označena jako y0, potom je vzorec
ve tvaru :
y y
y
y
k n 1 2 n n n
y
y
y0 y1
n 1
0
10.
Počítat průměrný koeficient růstu má smysl jen tehdy,vykazuje-li časová řada v podstatě monotónní vývoj.
11.
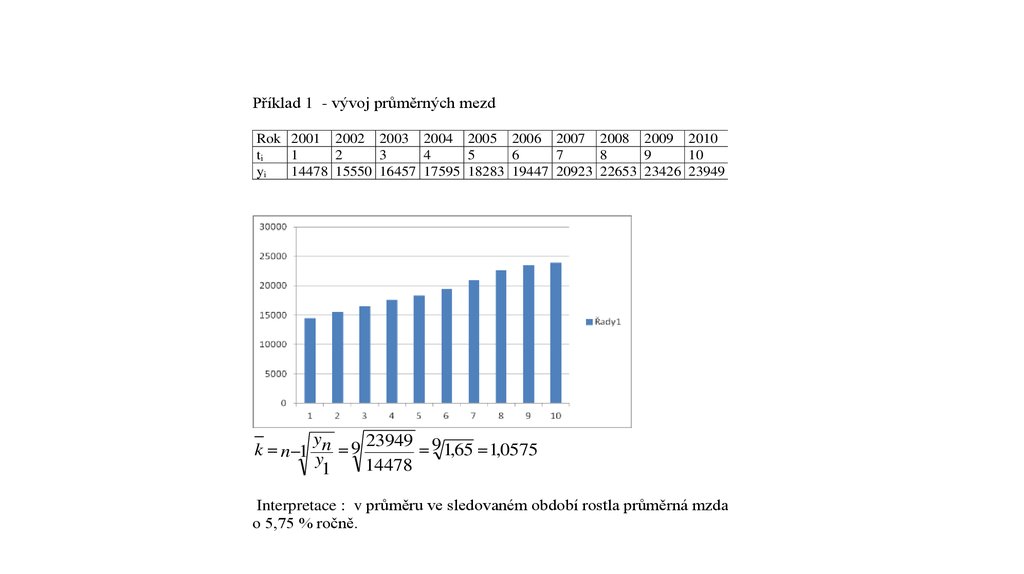
Příklad 1 - vývoj průměrných mezdRok 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010
ti
1
2
3
4
5
6
7
8
9
10
yi
14478 15550 16457 17595 18283 19447 20923 22653 23426 23949
y
23949 9
k n 1 n 9
1,65 1,0575
y
14478
1
Interpretace : v průměru ve sledovaném období rostla průměrná mzda
o 5,75 % ročně.
12.
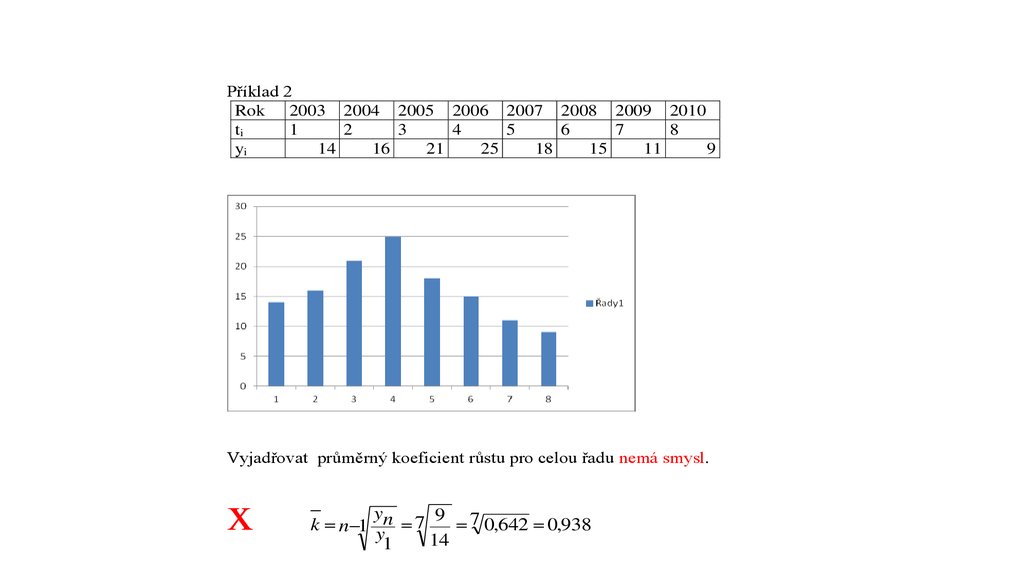
Příklad 2Rok
2003 2004 2005 2006 2007 2008 2009 2010
ti
1
2
3
4
5
6
7
8
yi
14
16
21
25
18
15
11
9
Vyjadřovat průměrný koeficient růstu pro celou řadu nemá smysl.
x
y
9 7
k n 1 n 7
0,642 0,938
y
14
1
13.
Rokti
yi
2003 2004 2005 2006 2007 2008 2009 2010
1
2
3
4
5
6
7
8
14
16
21
25
18
15
11
9
Můžeme pouze vyjádřit průměrné koeficienty růstu pro části řady, kde
je vývoj monotónní :
y
25 3
a) Pro roky 2003-2006 : k n 1 n 3
1,785 1,213
y
14
1
y
9 4
b) Pro roky 2006-2010 : k n 1 n 4
0,36 0,774
y
25
1
14. Bazické a řetězové indexy
ytKoeficient růstu kt
lze rovněž nazvat jako řetězový index –
y
t 1
hodnota ukazatele je porovnávána k hodnotě předchozího období
Bazické indexy - hodnota ukazatele je porovnávána k základu ( bázi)
yt
kt
y
0
15.
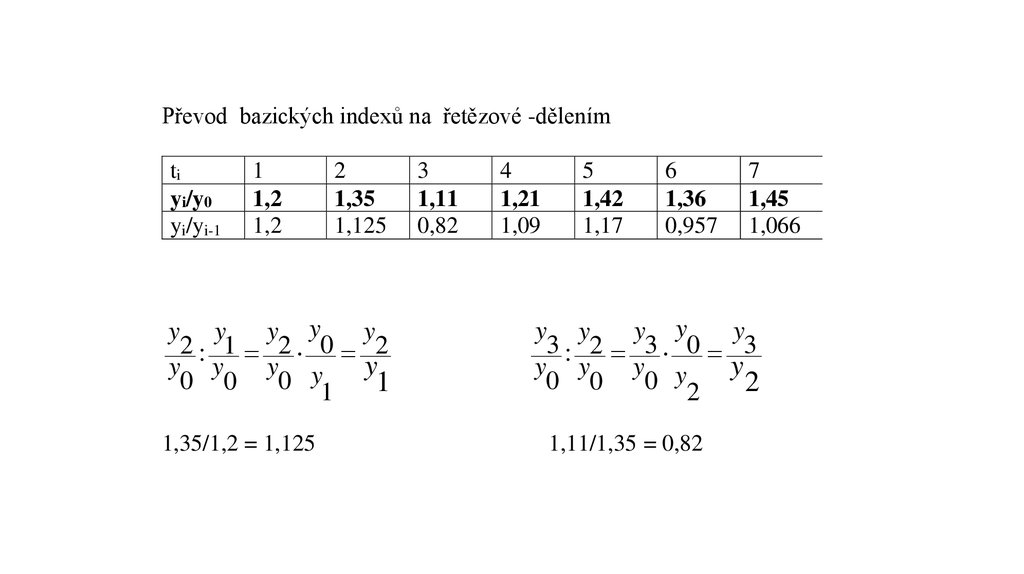
Převod bazických indexů na řetězové – dělenímy2/y0 : y1/y0
= y2/y0 . y0/y1 = y2/y1
Převod řetězových indexů na bazické – násobením
y y y
3 2 1
y y y
2 1 0
y
3
y
0
16.
Převod bazických indexů na řetězové -dělenímti
yi/y0
yi/yi-1
1
1,2
1,2
y y
2: 1
y y
0 0
2
1,35
1,125
y y
2 0
y y
0 1
1,35/1,2 = 1,125
y
2
y
1
3
1,11
0,82
4
1,21
1,09
5
1,42
1,17
6
1,36
0,957
y y
3: 2
y y
0 0
y y
3 0
y y
0 2
1,11/1,35 = 0,82
7
1,45
1,066
y
3
y
2
17.
Převod řetězových indexů na bazické – násobenímy0 …2004
ti
yi/yi-1
yi/y0
1
1,14
1,14
y y
2 1
y y
1 0
y
2
y
0
1,14*0,96 = 1,094
2
0,96
1,094
3
1,22
1,335
4
1,26
1,68
y y y
3 2 1
y y1 y0
2
5
0,97
1,63
y
3
y
0
1,22*0,96*1,14 = 1,335
6
1,10
1,79
7
1,18
2,11
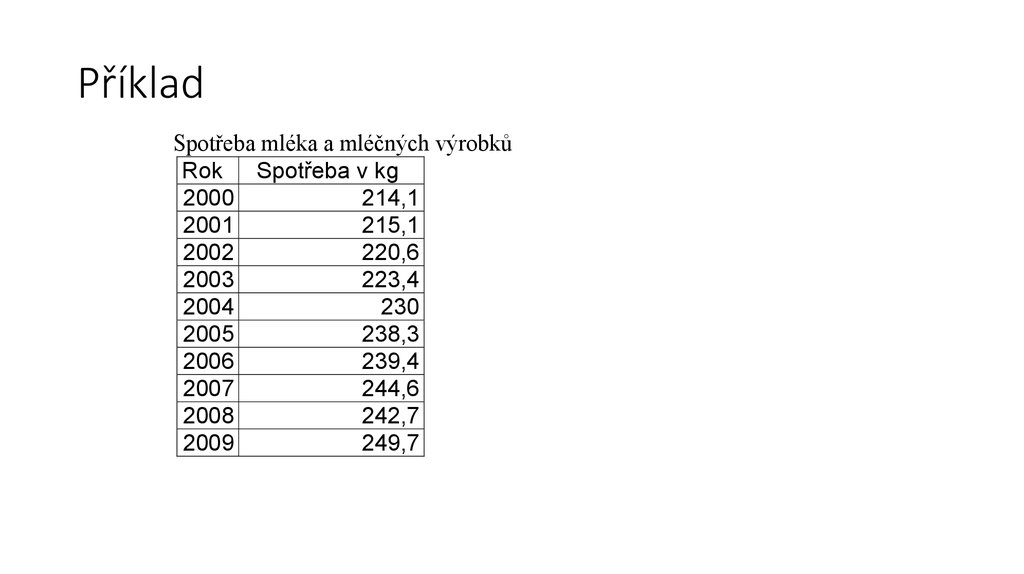
18. Příklad
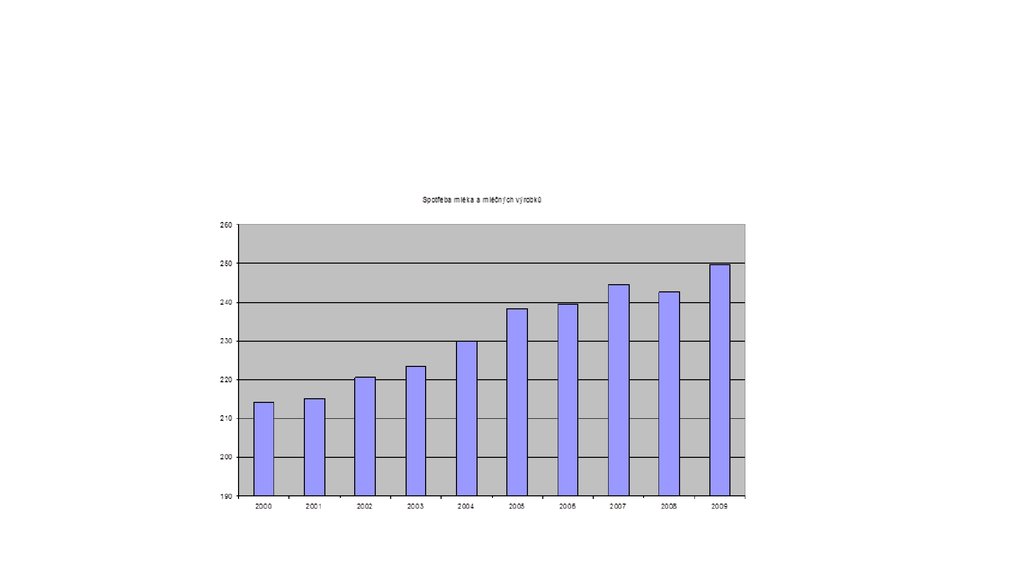
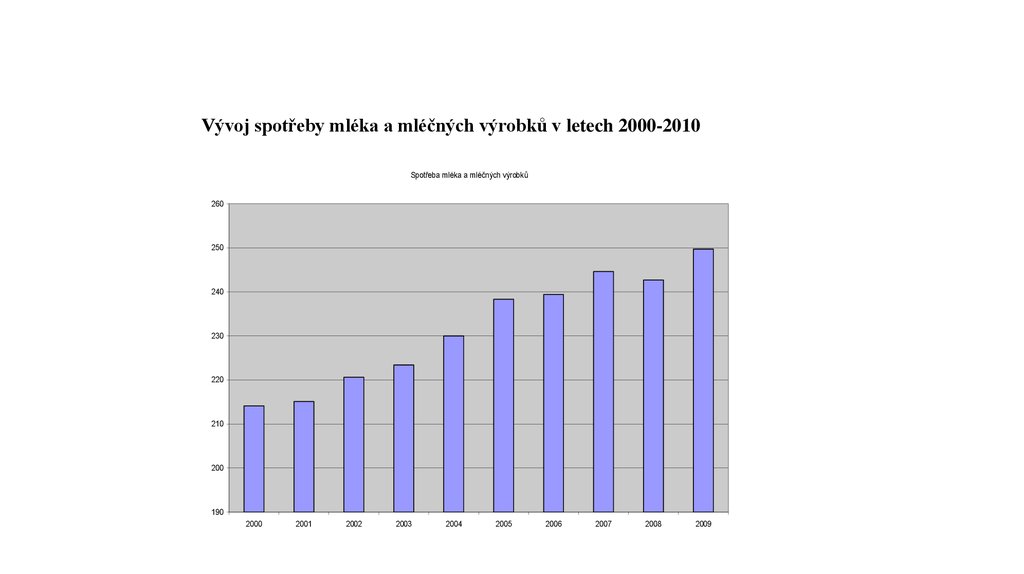
Spotřeba mléka a mléčných výrobkůRok Spotřeba v kg
2000
214,1
2001
215,1
2002
220,6
2003
223,4
2004
230
2005
238,3
2006
239,4
2007
244,6
2008
242,7
2009
249,7
19.
20.
Spotřeba mléka a mléčných výrobků – analýza vývojeRok
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
Σ
Spotřeba v kg
yi
yi/yi-1
yi-yi-1 yi/y0
yi-y0
214,1
215,1
1,005
1
1,005
1
220,6
1,026
5,5
1,030
6,5
223,4
1,013
2,8
1,043
9,3
230
1,030
6,6
1,074
15,9
238,3
1,036
8,3
1,113
24,2
239,4
1,005
1,1
1,118
25,3
244,6
1,022
5,2
1,142
30,5
242,7
0,992
-1,9
1,134
28,6
249,7
1,029
7
1,166
35,6
2317,9
Průměr časové řady
y
yi 2317,9
=
= 231,79
n
10
Průměrný koeficient růstu
y y
y
y
k n 1 2 3 n n 1 n
y y
y
y
1 2
n 1
1
k 9 249,7 = 1,017
214,1
21. Dekompozice časové řady
yt = Tt + Pt +ƐtSložky ČŘ
Trend - T
periodická kolísání - P
náhodná kolísání - Ɛ
22.
Trend charakterizuje dlouhodobou celkovou a hlavní tendenci vývoječasové řady.
Periodická složka je důsledkem působení periodicky se opakujících
faktorů na sledovaný jev, projevuje se periodickými výkyvy ukazatelů
časové řady okolo trendu (hodnoty v časové řadě mohou střídavě růst
nebo klesat). Podle délky jedné periody pak rozlišujeme:
- cyklické kolísání – perioda pravidelně se opakujících výkyvů
ukazatelů přesahuje období delší než jeden rok,
- sezónní kolísání – je charakteristické roční periodou,
- krátkodobé kolísání – periodické výkyvy časové řady se opakují
v rámci období kratšího než jeden rok.
Náhodné kolísání je vyvoláno působením vedlejších – pro daný případ
– faktorů náhodného charakteru. Projevuje se drobnými,
nepravidelnými nebo ojedinělými výkyvy časové řady, které není
možné předvídat
23. Postižení trendu - vyrovnávání časových řad
a) mechanické vyrovnání pomocí klouzavých průměrůMáme-li dánu časovou řadu y1 , y2, ….., yn, budeme klouzavými
průměry řádu k, též zvanými k-člennými klouzavými průměry, rozumět
posloupnost aritmetických průměrů.
y y y
1 2
k
k
y y y
3 4
k 2
k
y y y
2 3
k 1
k
24.
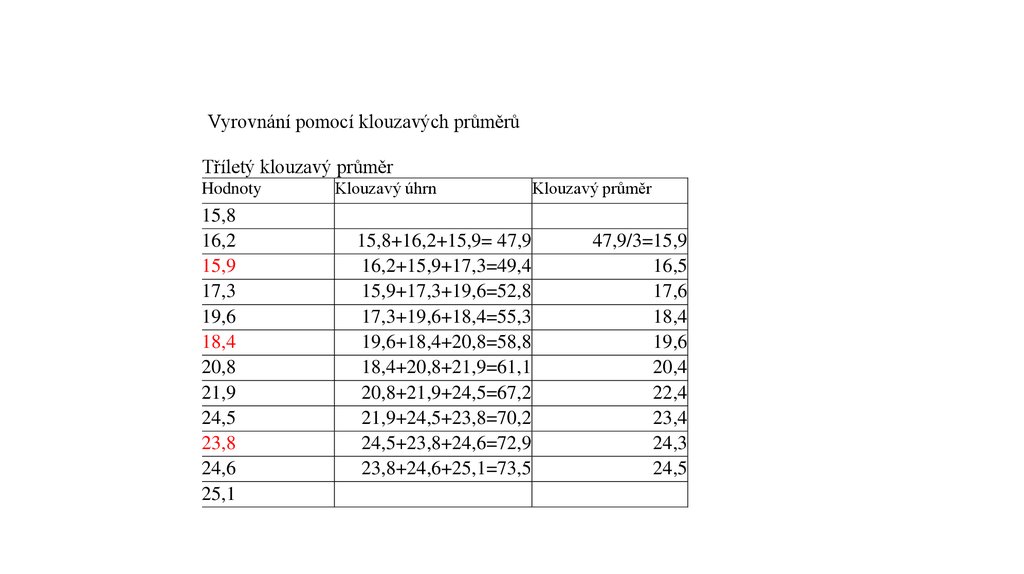
Vyrovnání pomocí klouzavých průměrůTříletý klouzavý průměr
Hodnoty
15,8
16,2
15,9
17,3
19,6
18,4
20,8
21,9
24,5
23,8
24,6
25,1
Klouzavý úhrn
15,8+16,2+15,9= 47,9
16,2+15,9+17,3=49,4
15,9+17,3+19,6=52,8
17,3+19,6+18,4=55,3
19,6+18,4+20,8=58,8
18,4+20,8+21,9=61,1
20,8+21,9+24,5=67,2
21,9+24,5+23,8=70,2
24,5+23,8+24,6=72,9
23,8+24,6+25,1=73,5
Klouzavý průměr
47,9/3=15,9
16,5
17,6
18,4
19,6
20,4
22,4
23,4
24,3
24,5
25.
26. b)vyrovnání analyticky - pomocí trendové funkce
Nejčastěji používané funkce :- lineární
Tt = a + bt
- kvadratická
Tt = a + bt + ct2
- logaritmická
Tt = a + b log t
- lomená
Tt = a + b/t
- exponenciální
Tt = a bt
mocninná
Tt = a tb
-
- odmocninná
Tt = a +b
- kombinovaná
Tt = a +bt + c
-logistická
Tt =
k
1 e a bt
t
t
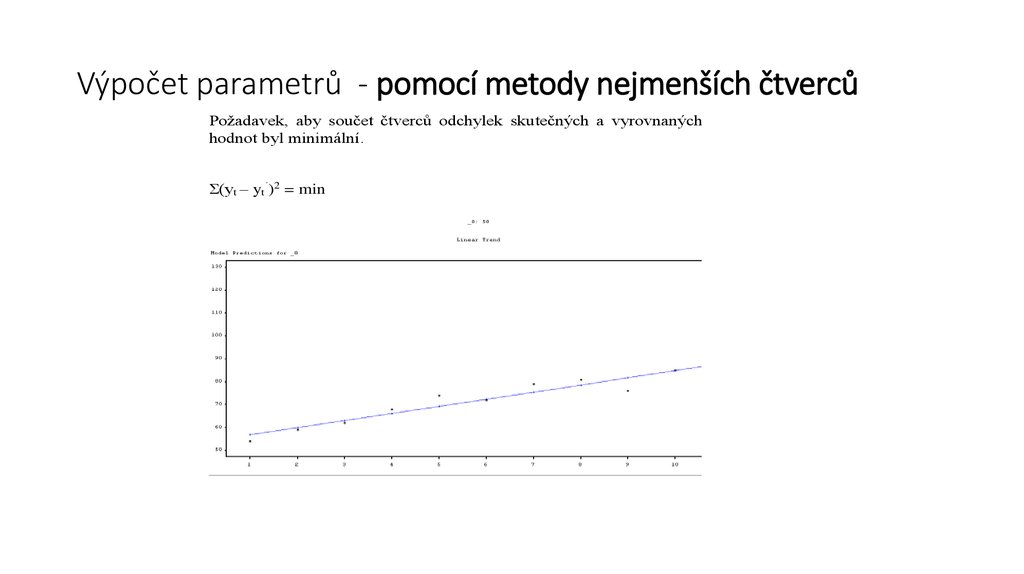
27. Výpočet parametrů - pomocí metody nejmenších čtverců
Výpočet parametrů - pomocí metody nejmenších čtvercůPožadavek, aby součet čtverců odchylek skutečných a vyrovnaných
hodnot byl minimální.
Σ(yt – yt´)2 = min
28.
Soustava normálních rovnic:Lineární trend ( přímka) :
na + b ti = yi
a ti + b ti2 = yiti
Kvadratický trend (parabola) :
na + b ti + c ti2 = yi
a ti + b ti2 + c ti3 = yiti
a ti2 + b ti3 + c ti4 = yiti2
Lomený trend ( hyperbola) :
na + b t1 = yi
i
a t1 +b t1 = yt
2
i
i
i
i
29. Posouzení vhodnosti modelu ( jak zvolený model popisuje minulost)
Index determinace2
(
y
y
)
i i
I2yt = 1 ( yi y)2
/
Index korelace Iyt
Koeficient korelace r ( v případě lineární trendové funkce)
30. Posouzení vhodnosti modelu ( jak zvolený model popisuje minulost)
Posouzení pomocí velikosti chybyM.E. – střední chyba odhadu
ME =
(y
t
y t )
n
M.S.E. = střední kvadratická chyba odhadu
MSE
t
yt yt 2
n k
et2
t n k
M.A.E. – střední absolutní chyba odhadu
MAE
1
y yt
n t t
M.A.P.E. – střední absolutní procentní chyba odhadu
yt yt
MAPE 100
n
yt
t
M.P.E. – střední procentní chyba odhadu
MPE
100 yt yt
n t yt
31. Posouzení vhodnosti prognózy
Pomocí pseudoprognózyČasová řada se zkrátí o několik údajů, vypočte se trend a prognóza na
období, která jsme z pozorování vyřadili. Známe tedy prognózu i
skutečnost. Porovnáním prognózy a skutečnosti lze potom zjistit, jak
vhodná prognóza je.
32. Charakteristiky
Relativní chyba prognózyr=
P S .100
S
P – prognóza
(%)
S - skutečnost
Theilův koeficient nesouladu
( S P)2
T =
S2
2
Relativní chyba extrapolace
T=
T 2 . 100
(%)
33.
Vývoj spotřeby mléka a mléčných výrobků v letech 2000-2010Spotřeba mléka a mléčných výrobků
260
250
240
230
220
210
200
190
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
34.
Lze popsat lineární trendovou funkcíy = a + b. ti
Řešení přes soustavu normálních rovnic :
na + b ti = yi
a ti + b ti2 = yiti
35.
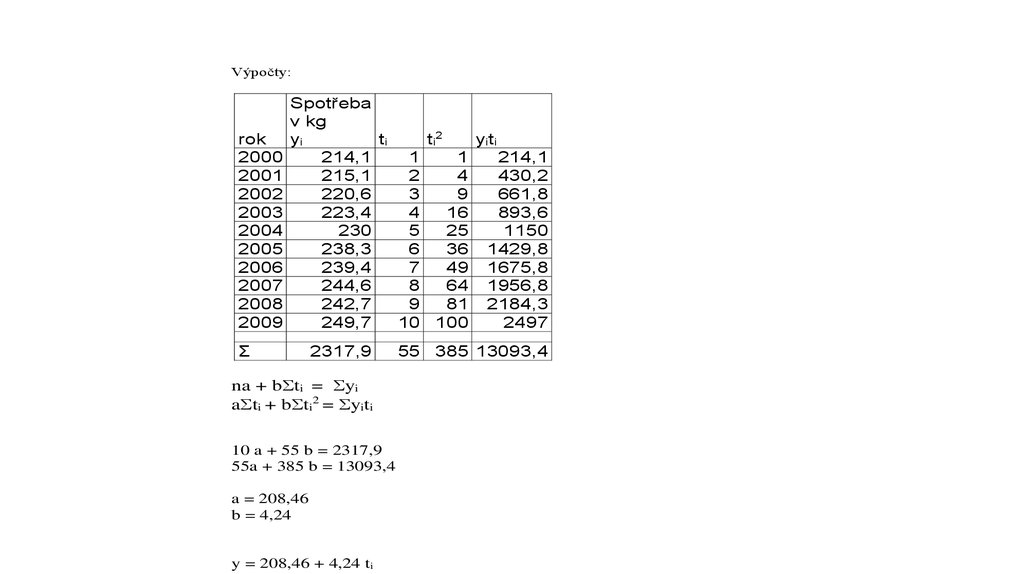
Výpočty:rok
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
Spotřeba
v kg
yi
ti
ti2
yiti
214,1
1
1
214,1
215,1
2
4
430,2
220,6
3
9
661,8
223,4
4
16
893,6
230
5
25
1150
238,3
6
36 1429,8
239,4
7
49 1675,8
244,6
8
64 1956,8
242,7
9
81 2184,3
249,7
10 100
2497
Σ
2317,9
na + b ti = yi
a ti + b ti2 = yiti
10 a + 55 b = 2317,9
55a + 385 b = 13093,4
a = 208,46
b = 4,24
y = 208,46 + 4,24 ti
55 385 13093,4
36.
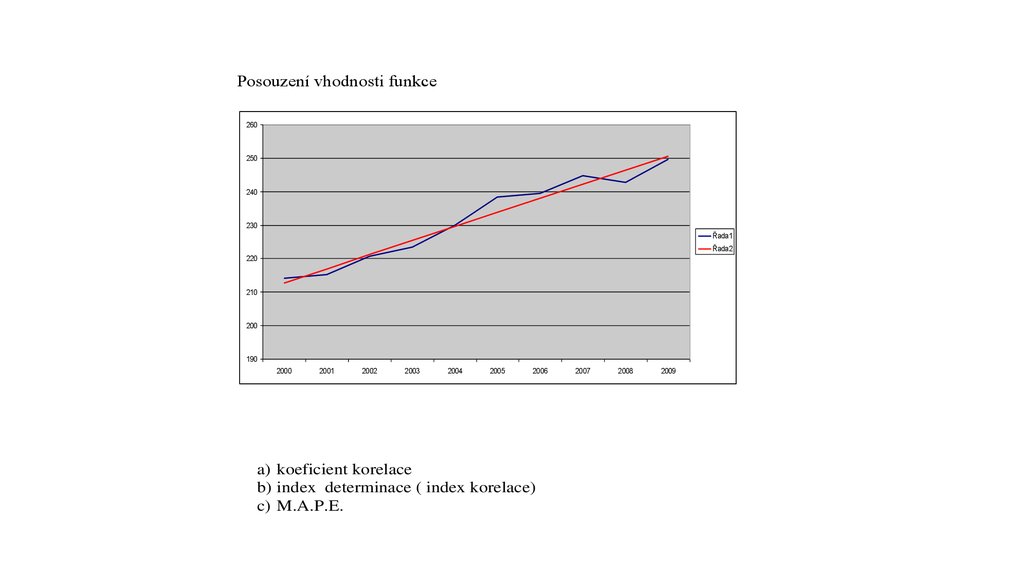
Posouzení vhodnosti funkce260
250
240
230
Řada1
Řada2
220
210
200
190
2000
2001
2002
2003
2004
2005
2006
a) koeficient korelace
b) index determinace ( index korelace)
c) M.A.P.E.
2007
2008
2009
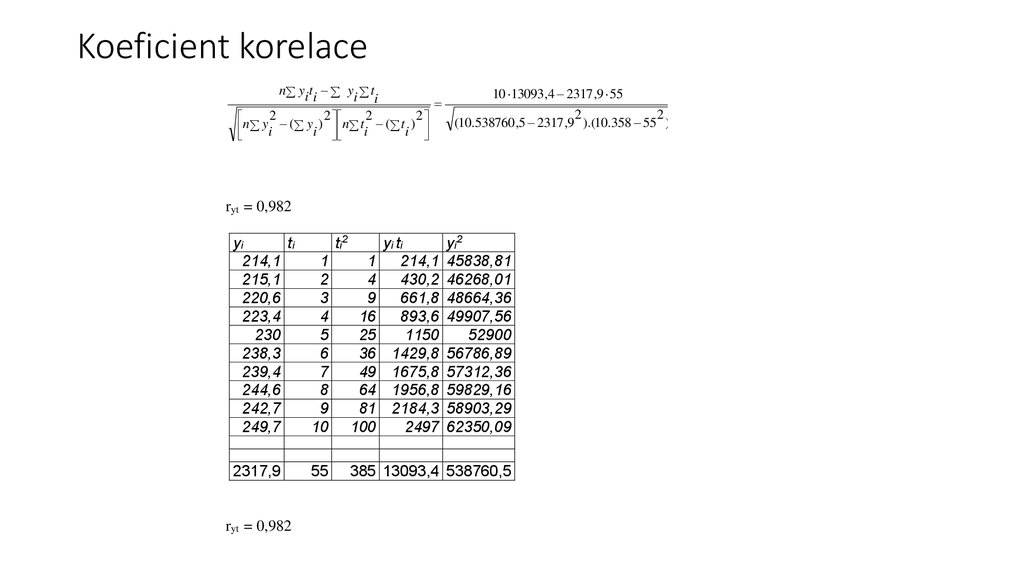
37. Koeficient korelace
n yi ti yi t10 13093,4 2317 ,9 55
i
2
2
2
2
2
2
(10.538760 ,5 2317 ,9 ).(10.358 55 )
n yi ( yi ) n ti ( ti )
ryt = 0,982
ti 2
1
2
3
4
5
6
7
8
9
10
1
4
9
16
25
36
49
64
81
100
2317,9
55
385 13093,4 538760,5
ryt = 0,982
y i ti
214,1
430,2
661,8
893,6
1150
1429,8
1675,8
1956,8
2184,3
2497
yi2
45838,81
46268,01
48664,36
49907,56
52900
56786,89
57312,36
59829,16
58903,29
62350,09
yi
ti
214,1
215,1
220,6
223,4
230
238,3
239,4
244,6
242,7
249,7
38. Index determinace ( index korelace)
( yi yi ) 252,5545
1
0,9648
I yt = 1 2
1494,489
( yi y)
/
2
y = 208,46 + 4,24 ti
y
yi
= 231,79
n
yi - y
(yi - y )2
yi´
yi – yi´ (yi – yi´)2
212,67
1,43
2,0449 -17,69 312,9361
216,88
-1,78
3,1684 -16,69 278,5561
221,09
-0,49
0,2401 -11,19 125,2161
225,3
-1,9
3,61
-8,39
70,3921
229,51
0,49
0,2401
-1,79
3,2041
233,72
4,58
20,9764
6,51
42,3801
237,93
1,47
2,1609
7,61
57,9121
242,14
2,46
6,0516
12,81 164,0961
246,35
-3,65
13,3225
10,91 119,0281
250,56
-0,86
0,7396
17,91 320,7681
yi
ti
214,1
215,1
220,6
223,4
230
238,3
239,4
244,6
242,7
249,7
1
2
3
4
5
6
7
8
9
10
2317,9
55 2316,15
I2yt = 0,9648
Iyt = 0,982
52,5545
1494,489
39. M.A.P.E.
y y100
MAPE n i y i
i
yi
ti yi´
214,1 1
215,1 2
220,6 3
223,4 4
230 5
238,3 6
239,4 7
244,6 8
242,7 9
249,7 10
2317,9 55
Іyi - yi´І
212,67
216,88
221,09
225,3
229,51
233,72
237,93
242,14
246,35
250,56
2316,15
M.A.P.E. = 10 . 0,0817 = 0,817 %
1,43
1,78
0,49
1,9
0,49
4,58
1,47
2,46
3,65
0,86
І(yi - yi´)/ yi І
0,006679
0,008275
0,002221
0,008505
0,00213
0,019219
0,00614
0,010057
0,015039
0,003444
0,081711
40. Vhodnost prognózy
Pomocí pseudoprognózyŘadu zkrátíme o jedno pozorování, pro tuto zkrácenou řadu vypočteme
lineární trendovou funkci a pro hodnotu roku 2010 vypočteme
prognózu (pseudoprognózu) a porovnáme se známou skutečností.
41.
yi214,1
215,1
220,6
223,4
230
238,3
239,4
244,6
242,7
ti
1
2
3
4
5
6
7
8
9
2068,2
45
ti 2
1
4
9
16
25
36
49
64
81
yiti
214,1
430,2
661,8
893,6
1150
1429,8
1675,8
1956,8
2184,3
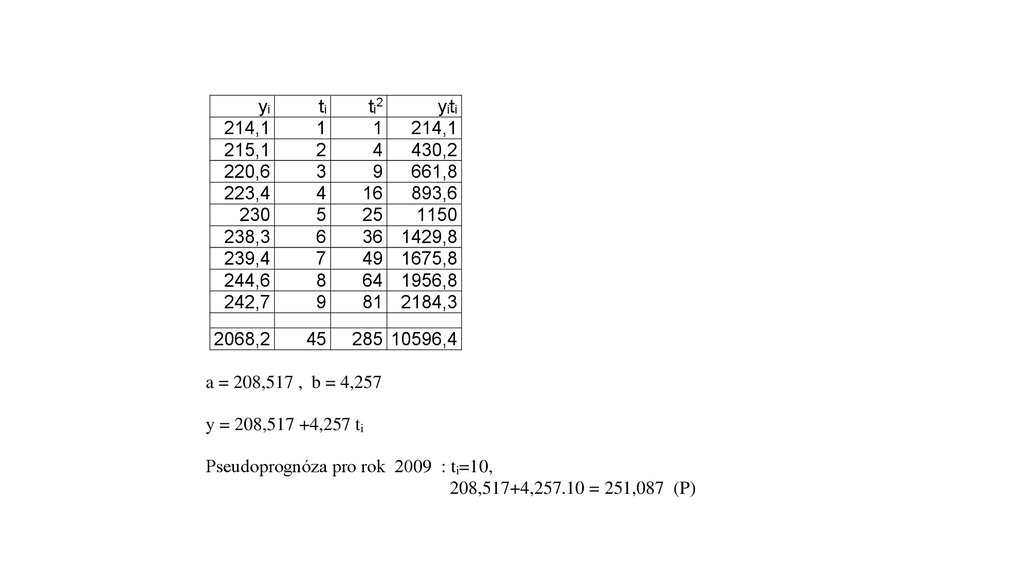
285 10596,4
a = 208,517 , b = 4,257
y = 208,517 +4,257 ti
Pseudoprognóza pro rok 2009 : ti=10,
208,517+4,257.10 = 251,087 (P)
42.
Pseudoprognóza pro rok 2009 : ti=10,208,517+4,257.10 = 251,087 (P)
Skutečnost roku 2009 = 249,7 (S)
Relativní chyba prognózy
P S .100 (%)
S
251,087 249,4.100= 0,67%
=
249,4
r=
r
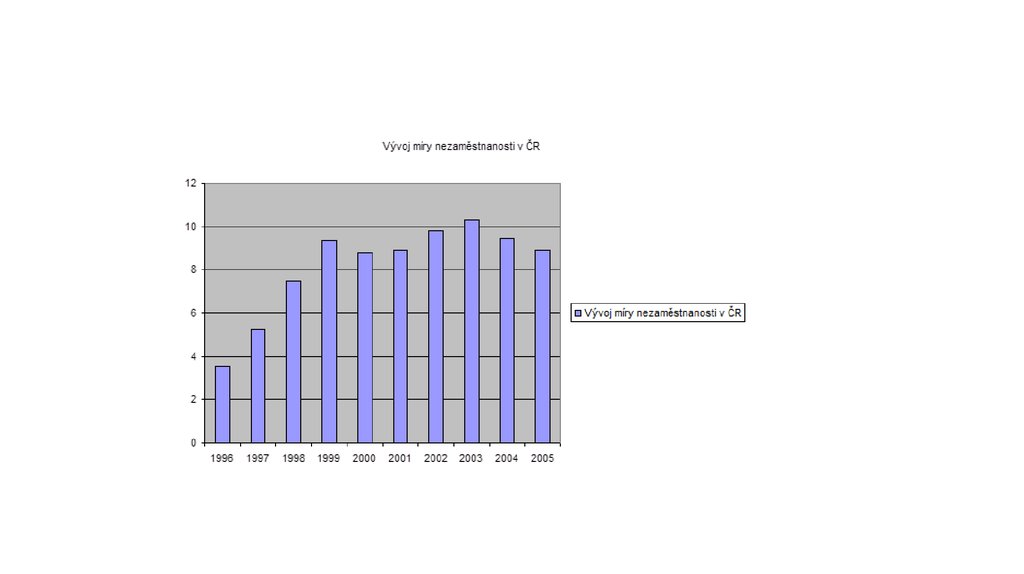
43. Příklad – vývoj míry nezaměstnanosti
Rok Míra nezaměstnanosti v %1996
3,52
1997
5,23
1998
7,48
1999
9,37
2000
8,78
2001
8,9
2002
9,81
2003
10,31
2004
9,47
2005
8,9
44.
45.
Vyrovnání pomocí kvadratické trendové funkce: y = a +b.t +c.t2Soustava normálních rovnic :
na + b ti + c ti2 = yi
a ti + b ti2 + c ti3 = yiti
a ti2 + b ti3 + c ti4 = yiti2
46.
Výpočty :1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
yi
3,52
5,23
7,48
9,37
8,78
8,9
9,81
10,31
9,47
8,9
ti
1
2
3
4
5
6
7
8
9
10
ti2
1
4
9
16
25
36
49
64
81
100
ti3
1
8
27
64
125
216
343
512
729
1000
ti4
1
16
81
256
625
1296
2401
4096
6561
10000
yiti
3,52
10,46
22,44
37,48
43,9
53,4
68,67
82,48
85,23
89
yiti2
3,52
20,92
67,32
149,92
219,5
320,4
480,69
659,84
767,07
890
81,77
55
385
3025
25333
496,58
3579,18
385 c = 81,77
10 a + 55 b +
55 a + 385b + 3025 c = 496,58
385a + 3025b + 25333 c = 3579,18
a = 1,533
b = 2,328 c = -0,16
yi/ = 1,533 +2,328 ti - 0,16 ti2
47.
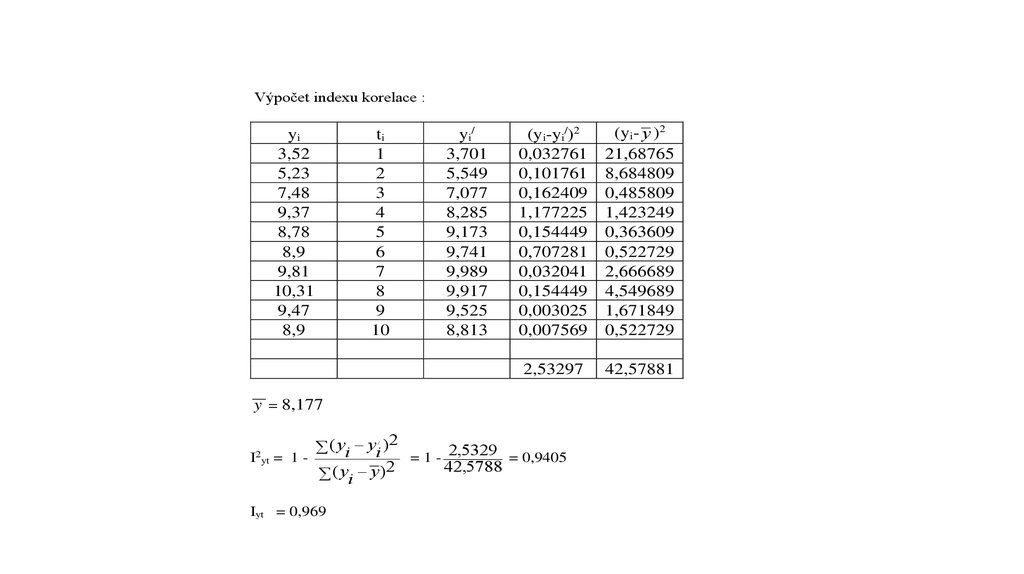
Výpočet indexu korelace :yi
3,52
5,23
7,48
9,37
8,78
8,9
9,81
10,31
9,47
8,9
ti
1
2
3
4
5
6
7
8
9
10
yi/
3,701
5,549
7,077
8,285
9,173
9,741
9,989
9,917
9,525
8,813
(yi-yi/)2
0,032761
0,101761
0,162409
1,177225
0,154449
0,707281
0,032041
0,154449
0,003025
0,007569
(yi- y )2
21,68765
8,684809
0,485809
1,423249
0,363609
0,522729
2,666689
4,549689
1,671849
0,522729
2,53297
42,57881
y = 8,177
( yi yi ) 2
I yt = 1 = 1 - 2,5329 = 0,9405
42,5788
( yi y) 2
/
2
Iyt = 0,969
48.
Prognóza y´2006 = 1,53+2,328. 11 – 0,16. 121= 7,78Skutečnost roku 2006 = 7,67
Relativní chyba předpovědi - 1,41%
























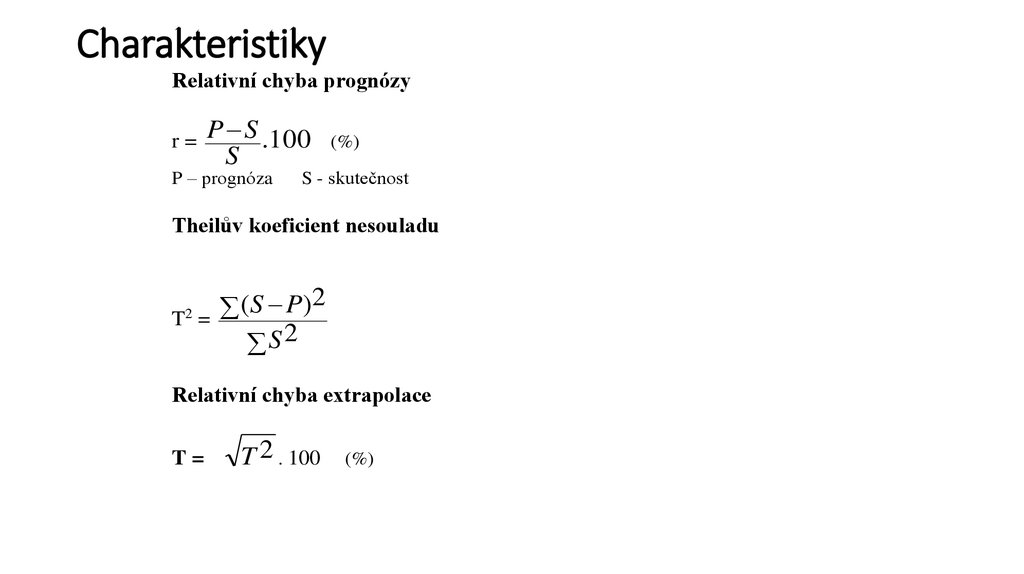









 mathematics
mathematics








