Periodické časové řady. Sezónnost v časových řadách

1. Periodické časové řady

2. Sezónnost v časových řadách

Periodická složka je důsledkem působení periodicky se opakujících
faktorů na sledovaný jev, projevuje se periodickými výkyvy ukazatelů
časové řady okolo trendu (hodnoty v časové řadě mohou střídavě růst
nebo klesat). Podle délky jedné periody pak rozlišujeme:
- cyklické kolísání – perioda pravidelně se opakujících výkyvů
ukazatelů přesahuje období delší než jeden rok,
- sezónní kolísání – je charakteristické roční periodou,
- krátkodobé kolísání – periodické výkyvy časové řady se opakují
v rámci období kratšího než jeden rok.

3.

Popis kolísání pomocí sezónních indexů a sezónních faktorů
Sezónní index : si =
yi
hodnota vyrovnaná
yi – hodnota skutečná
vyrovnaná hodnota - průměr řady
průměr za rok
klouzavé průměry
hodnota vyjádřená z trendové funkce

4.

Sezónní faktor
Součet průměrných sezónních indexů by měl být roven počtu
analyzovaných sezón. Pokud tomu tak není, je třeba provést přepočet.
Jedná se o jednoducho standardizaci sezónních indexů. Upravené
sezónní indexy pak nazýváme sezónní faktory.

5.

Postup :
Výpočet trendové funkce
Výpočet vyrovnaných hodnot ( z funkce )
Výpočet sezónních indexů : si =
y
i
y´
i
Výpočet průměrných sezónních indexů pro jednotlivá období

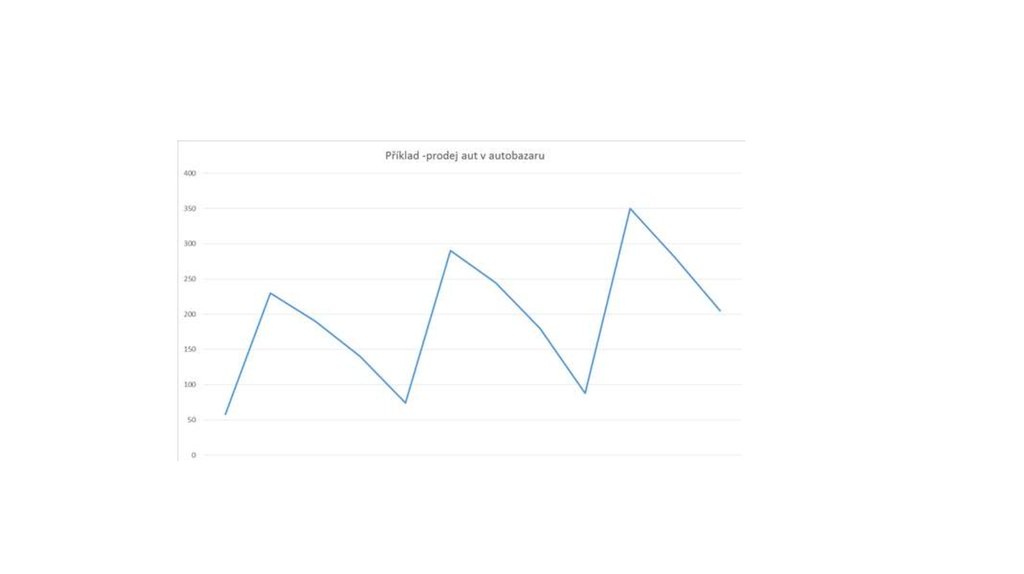
6. PŘÍKLAD

Prodej automobilů v autobazaru
rok
2013
2014
2015
1. čtvrtletí
58
74
88
2. čtvrtletí
230
290
350
3. čtvrtletí
190
245
280
4. čtvrtletí
140
180
205

7.

8.

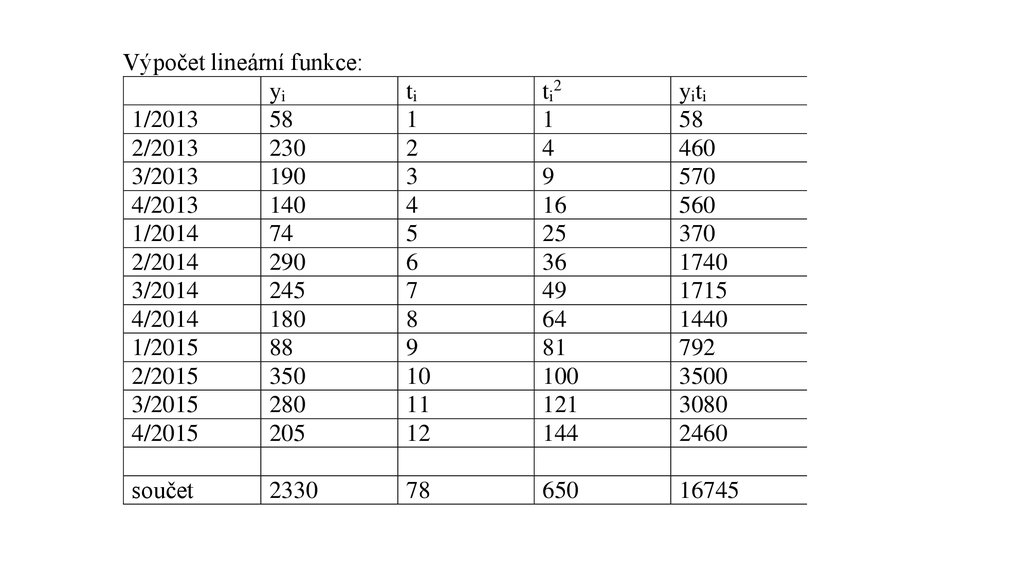
Výpočet lineární funkce:
yi
1/2013
58
2/2013
230
3/2013
190
4/2013
140
1/2014
74
2/2014
290
3/2014
245
4/2014
180
1/2015
88
2/2015
350
3/2015
280
4/2015
205
součet
2330
ti
1
2
3
4
5
6
7
8
9
10
11
12
ti2
1
4
9
16
25
36
49
64
81
100
121
144
yiti
58
460
570
560
370
1740
1715
1440
792
3500
3080
2460
78
650
16745

9.

Rovnice :
12 a + 78 b = 2330
78 a + 650 b = 16745
a = 121,43
b = 11,19
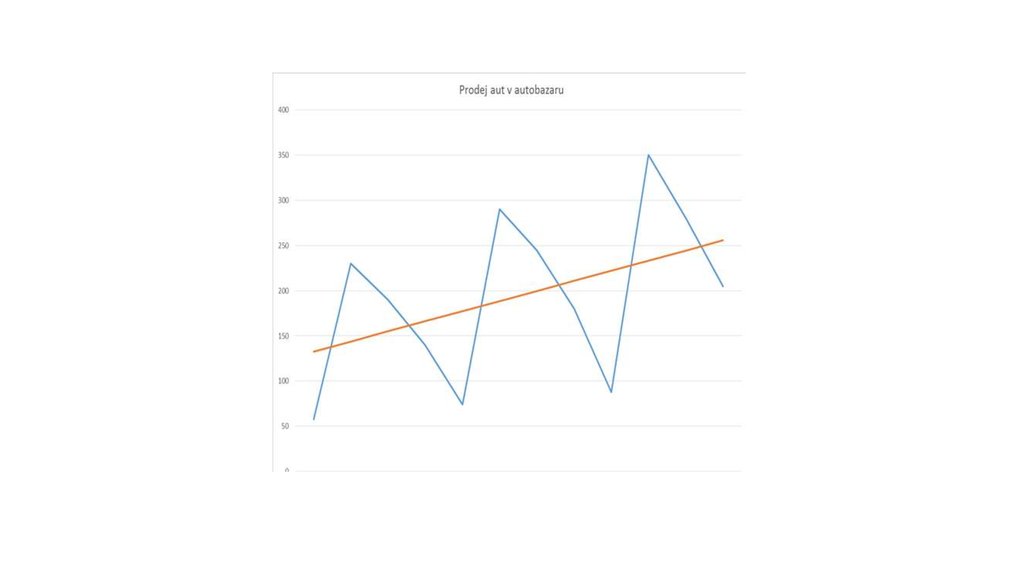
y´= 121,43 + 11,19 ti

10.

11.   Výpočet vyrovnaných hodnot a vyjádření sezónních indexů

Výpočet vyrovnaných hodnot a vyjádření sezónních indexů
yi
58
230
190
140
74
290
245
180
88
350
280
205
ti
1
2
3
4
5
6
7
8
9
10
11
12
yí
132,62
143,81
155
166,19
177,38
188,57
199,76
210,95
222,14
233,33
244,52
255,71
si= yi´
yi
0,43734
1,599332
1,225806
0,842409
0,417183
1,53789
1,226472
0,853283
0,396147
1,500021
1,145101
0,801689

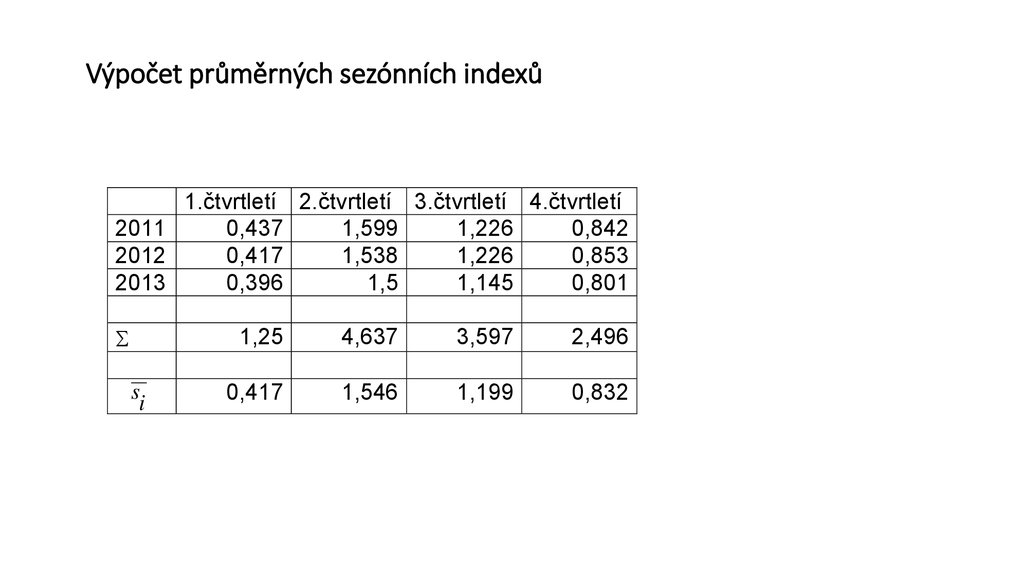
12. Výpočet průměrných sezónních indexů

1.čtvrtletí 2.čtvrtletí 3.čtvrtletí 4.čtvrtletí
0,842
1,226
1,599
0,437
2011
0,853
1,226
1,538
0,417
2012
0,801
1,145
1,5
0,396
2013
si
1,25
4,637
3,597
2,496
0,417
1,546
1,199
0,832

13.

Odhad prodeje - 2. čtvrtletí roku 2016
ti = 14
y´i = 121,43 + 11,19 . 14 = 278,09
sezónní index pro 2. čtvrtletí - s
odhad - 278,09 . 1,546 = 429,9
2
= 1,546

14. Korelace časových řad

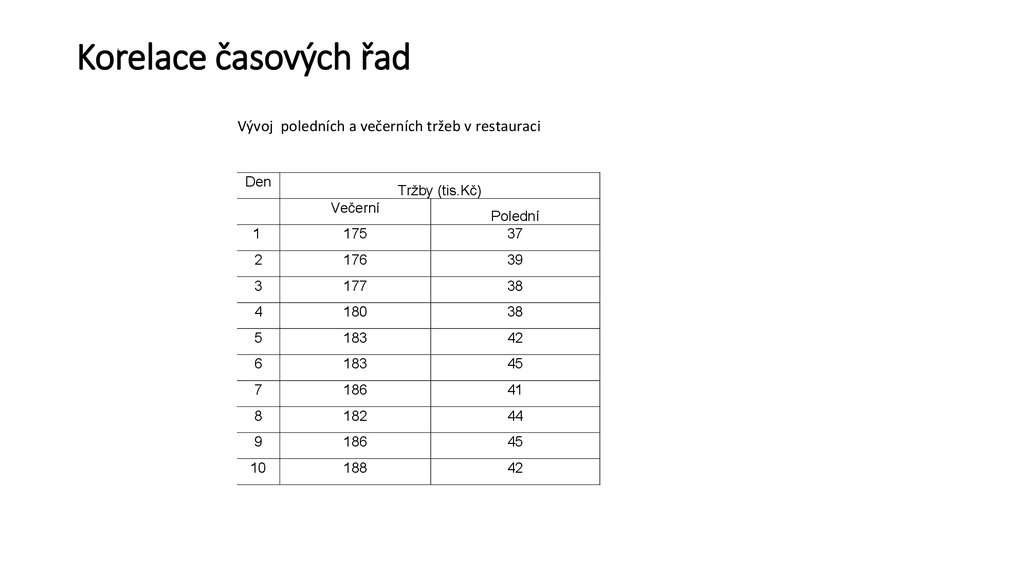
Vývoj poledních a večerních tržeb v restauraci
Den
Tržby (tis.Kč)
Večerní
1
175
Polední
37
2
176
39
3
177
38
4
180
38
5
183
42
6
183
45
7
186
41
8
182
44
9
186
45
10
188
42

15.

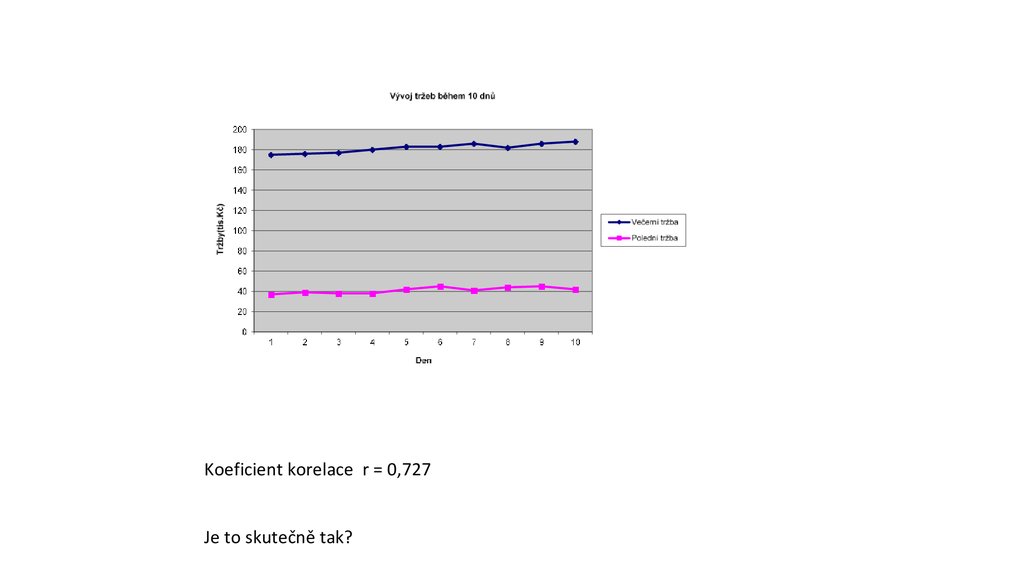
Koeficient korelace r = 0,727
Je to skutečně tak?

16.

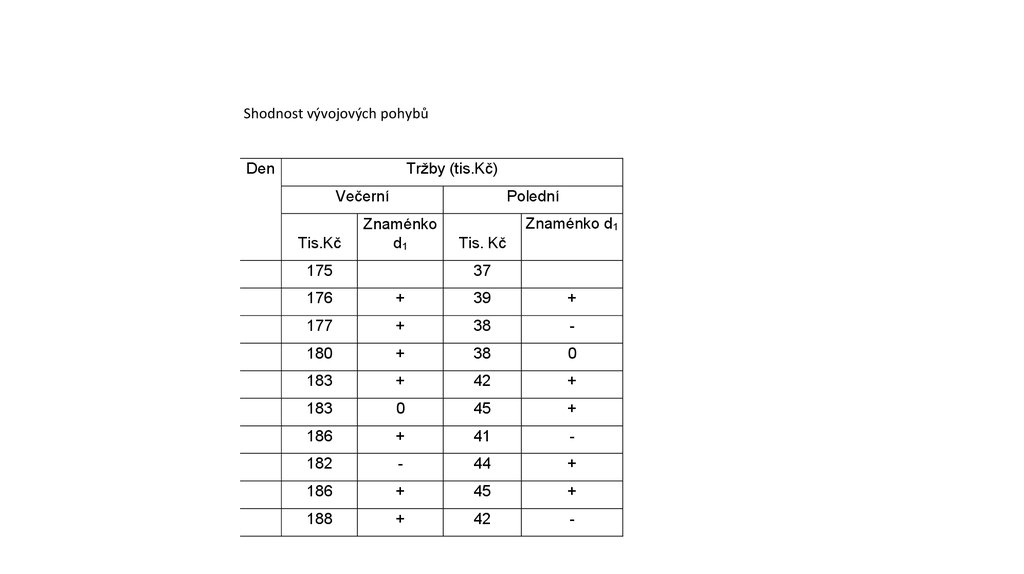
Shodnost vývojových pohybů
Tržby (tis.Kč)
Den
Večerní
Tis.Kč
Polední
Znaménko
d1
175
Znaménko d1
Tis. Kč
37
176
+
39
+
177
+
38
-
180
+
38
0
183
+
42
+
183
0
45
+
186
+
41
-
182
-
44
+
186
+
45
+
188
+
42
-

17.

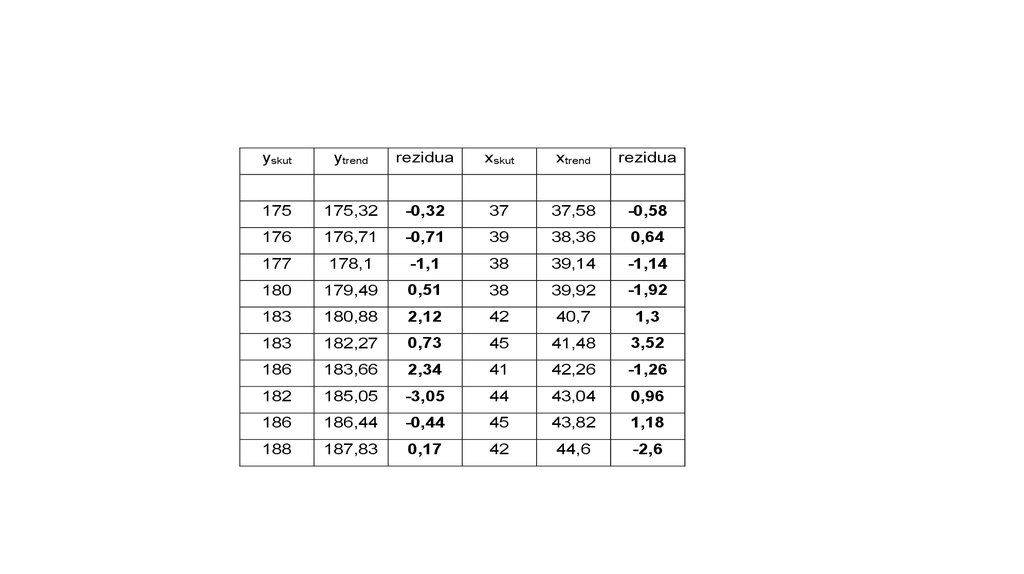
Korelace reziduí
a) vyjádříme trend
b) odečtením vyrovnaných hodnot (trend) získáme rezidua
c) vyjádříme koeficient korelace mezi reziduy
Funkce :
y´= 173,93 + 1,39 t
x´= 36,8 + 0,78t
r = 0,937 – vývoj večerních tržeb
r = 0,79 - vývoj poledních tržeb

18.

yskut
ytrend
rezidua
xskut
xtrend
rezidua
175
175,32
-0,32
37
37,58
-0,58
176
176,71
-0,71
39
38,36
0,64
177
178,1
-1,1
38
39,14
-1,14
180
179,49
0,51
38
39,92
-1,92
183
180,88
2,12
42
40,7
1,3
183
182,27
0,73
45
41,48
3,52
186
183,66
2,34
41
42,26
-1,26
182
185,05
-3,05
44
43,04
0,96
186
186,44
-0,44
45
43,82
1,18
188
187,83
0,17
42
44,6
-2,6

19.

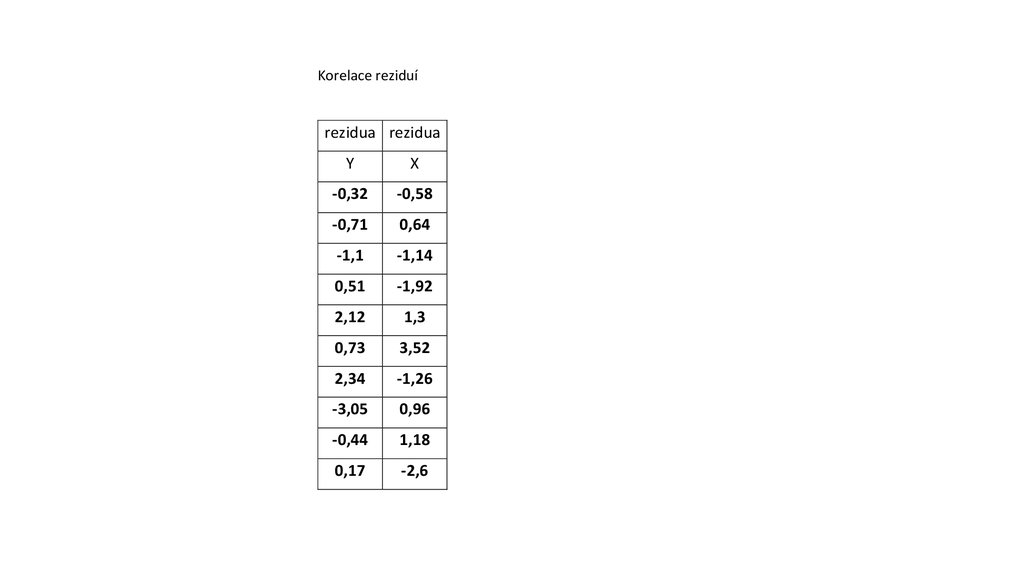
Korelace reziduí
rezidua rezidua
Y
X
-0,32
-0,58
-0,71
0,64
-1,1
-1,14
0,51
-1,92
2,12
1,3
0,73
3,52
2,34
-1,26
-3,05
0,96
-0,44
1,18
0,17
-2,6

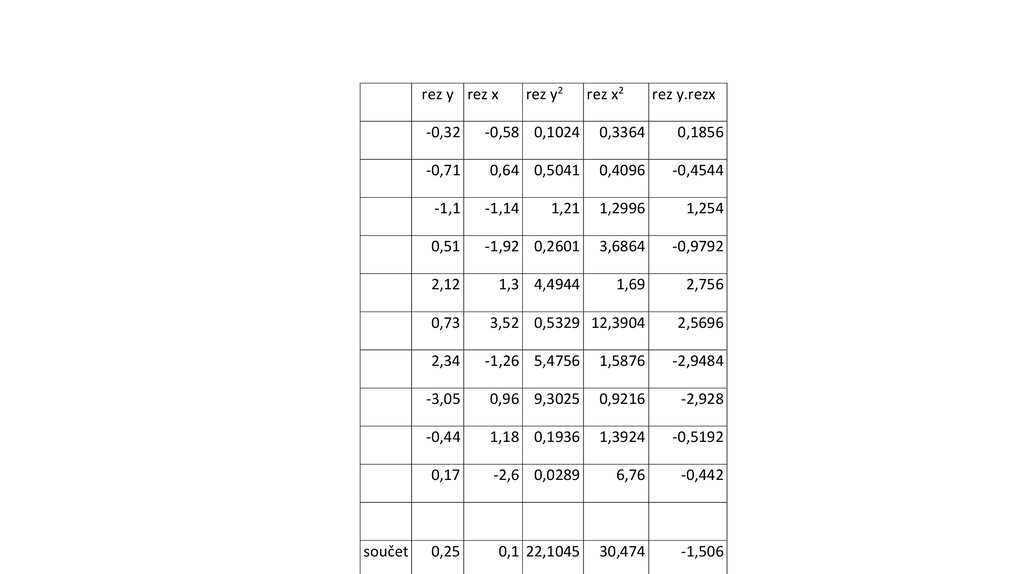
20. Výpočet koeficientu korelace z reziduí

Výpočet koeficientu korelace z reziduí
n yi xi yi x
i
r yx
2
2
2
2
n
y
(
y
)
n
x
(
x
)
i i
i
i

21.

rez y rez x
rez x2
rez y.rezx
-0,32
-0,58 0,1024
0,3364
0,1856
-0,71
0,64 0,5041
0,4096
-0,4544
-1,1
-1,14
1,21
1,2996
1,254
0,51
-1,92 0,2601
3,6864
-0,9792
2,12
1,3 4,4944
1,69
2,756
3,52 0,5329 12,3904
2,5696
0,73
součet
rez y2
2,34
-1,26 5,4756
1,5876
-2,9484
-3,05
0,96 9,3025
0,9216
-2,928
-0,44
1,18 0,1936
1,3924
-0,5192
0,17
-2,6 0,0289
6,76
-0,442
0,25
0,1 22,1045
30,474
-1,506

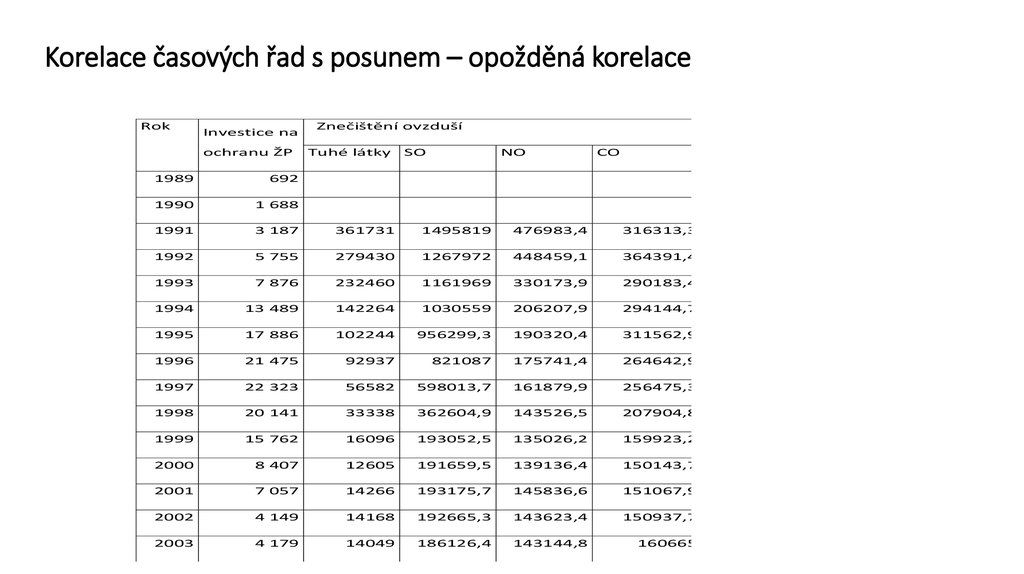
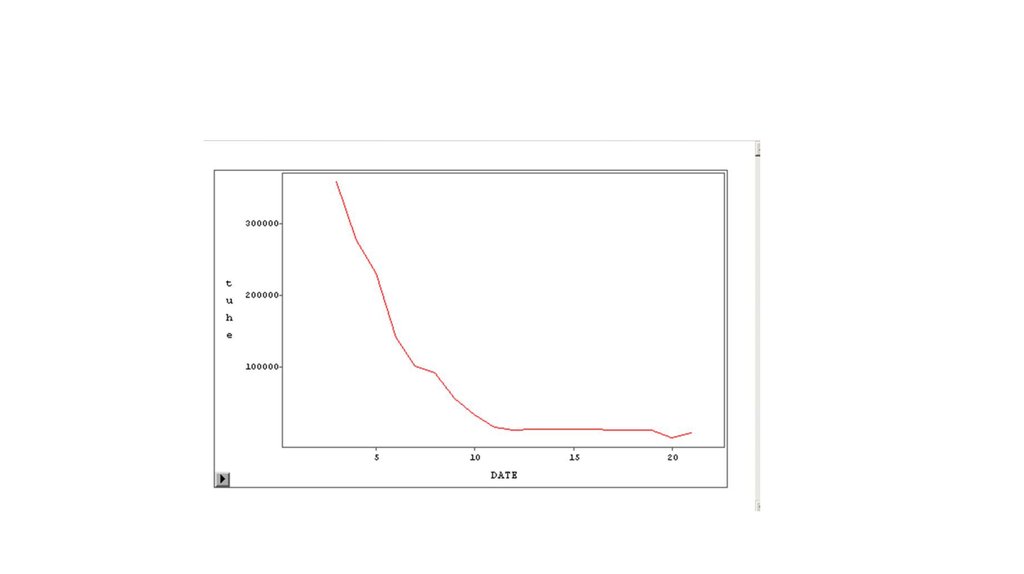
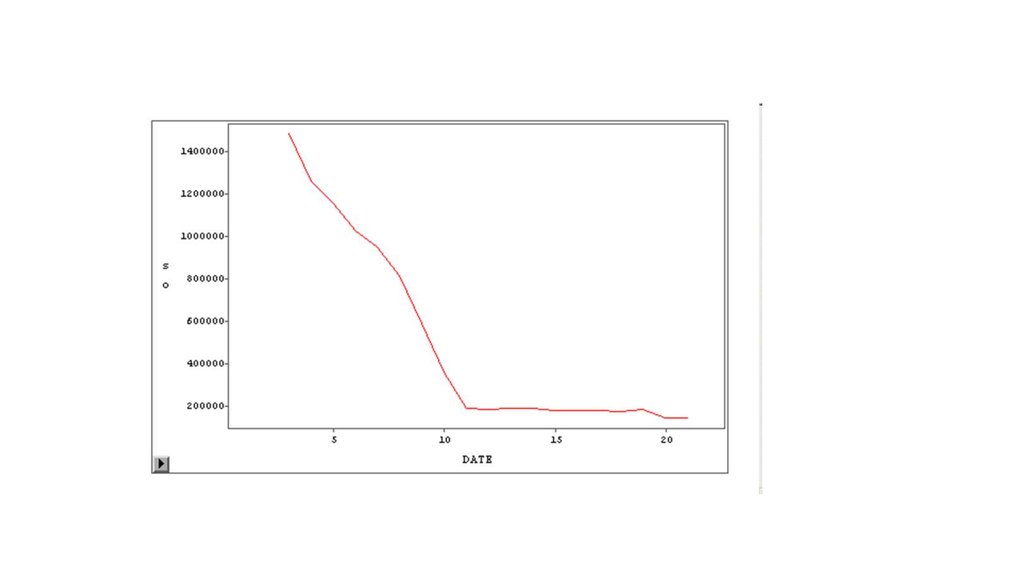
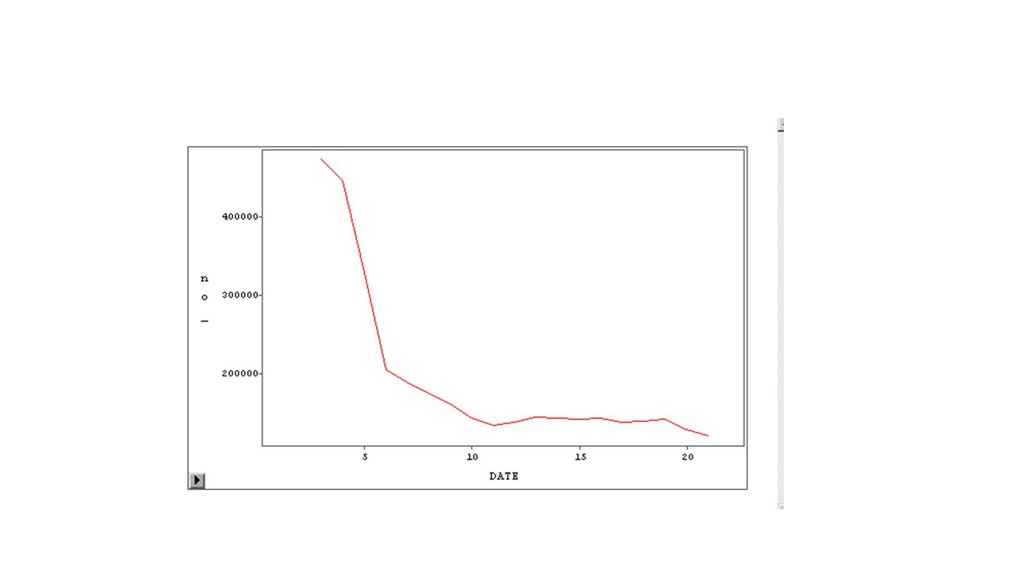
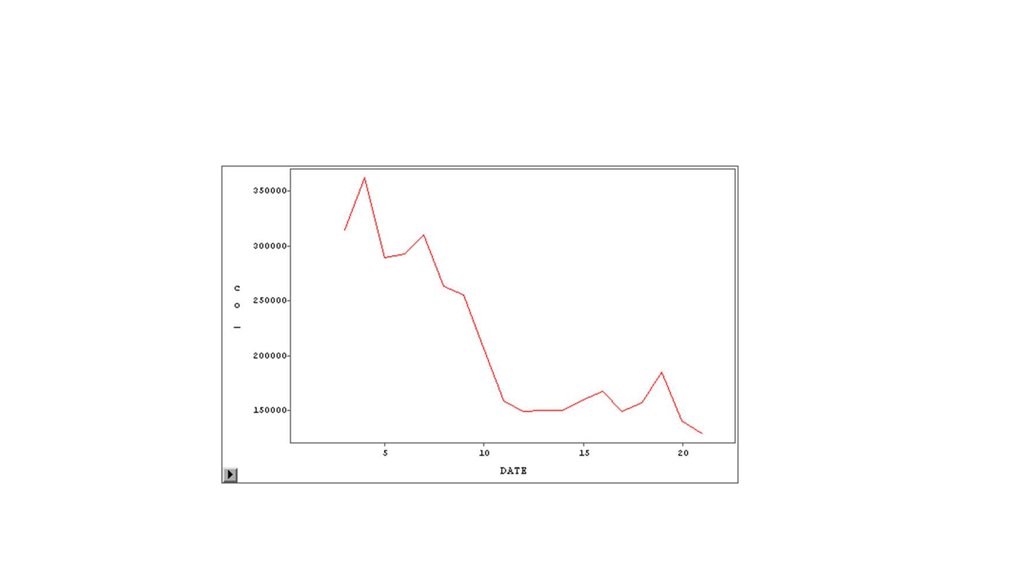
22. Korelace časových řad s posunem – opožděná korelace

Korelace časových řad s posunem – opožděná korelace
Rok
Investice na
ochranu ŽP
Znečištění ovzduší
Tuhé látky
SO
NO
CO
1989
692
1990
1 688
1991
3 187
361731
1495819
476983,4
316313,3
1992
5 755
279430
1267972
448459,1
364391,4
1993
7 876
232460
1161969
330173,9
290183,4
1994
13 489
142264
1030559
206207,9
294144,7
1995
17 886
102244
956299,3
190320,4
311562,9
1996
21 475
92937
821087
175741,4
264642,9
1997
22 323
56582
598013,7
161879,9
256475,3
1998
20 141
33338
362604,9
143526,5
207904,8
1999
15 762
16096
193052,5
135026,2
159923,2
2000
8 407
12605
191659,5
139136,4
150143,7
2001
7 057
14266
193175,7
145836,6
151067,9
2002
4 149
14168
192665,3
143623,4
150937,7
2003
4 179
14049
186126,4
143144,8
160665

23.

2004
4 677
13229
184365,3
143542,5
168388,3
2005
3 920
12442
184396,8
139185,1
149997,1
2006
4 562
12059
181062,2
139543,2
157488,8
2007
5 906
12467
189314,3
142133,8
185831,7
2008
3 841
999
149253,6
129794,5
141587,2
2009
3 633
8458
146698,3
120752,3
129422,3

24.

25.

26.

27.

28.

29.

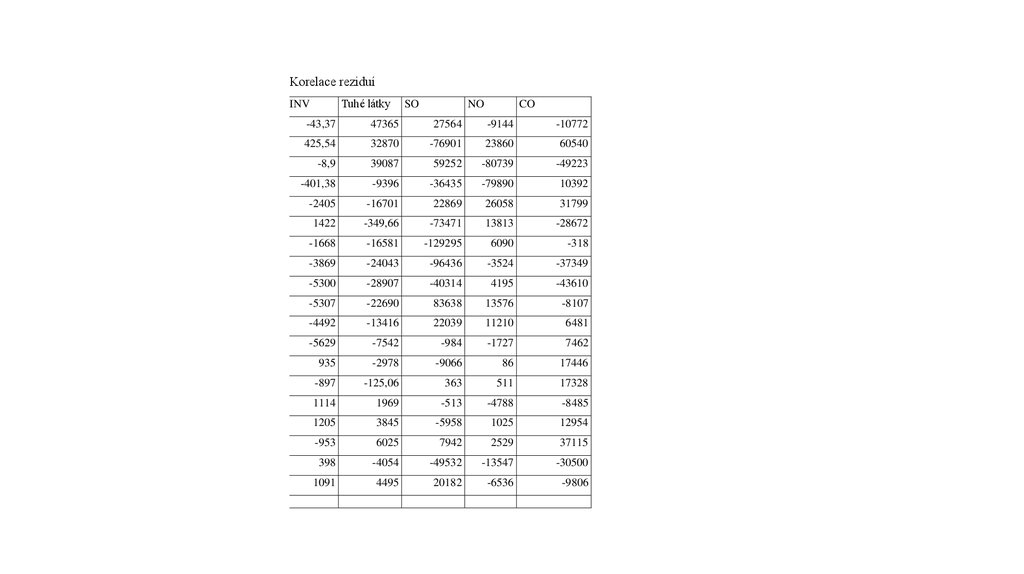
Korelace reziduí
Tuhé látky
INV
SO
NO
CO
-43,37
47365
27564
-9144
-10772
425,54
32870
-76901
23860
60540
-8,9
39087
59252
-80739
-49223
-401,38
-9396
-36435
-79890
10392
-2405
-16701
22869
26058
31799
1422
-349,66
-73471
13813
-28672
-1668
-16581
-129295
6090
-318
-3869
-24043
-96436
-3524
-37349
-5300
-28907
-40314
4195
-43610
-5307
-22690
83638
13576
-8107
-4492
-13416
22039
11210
6481
-5629
-7542
-984
-1727
7462
935
-2978
-9066
86
17446
-897
-125,06
363
511
17328
1114
1969
-513
-4788
-8485
1205
3845
-5958
1025
12954
-953
6025
7942
2529
37115
398
-4054
-49532
-13547
-30500
1091
4495
20182
-6536
-9806

30.

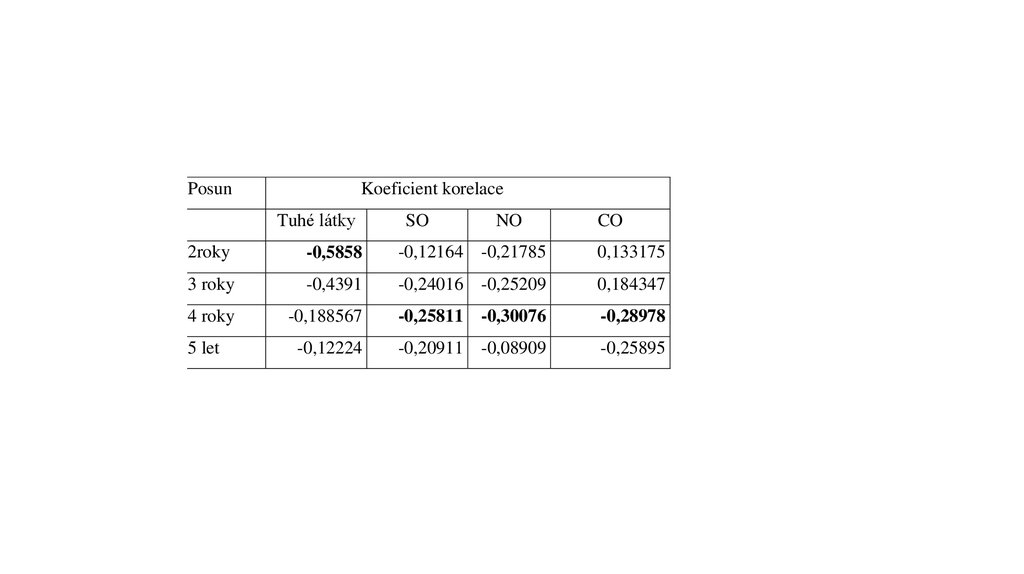
Posun
Koeficient korelace
Tuhé látky
SO
NO
CO
2roky
-0,5858
-0,12164 -0,21785
0,133175
3 roky
-0,4391
-0,24016 -0,25209
0,184347
4 roky
-0,188567
-0,25811 -0,30076
-0,28978
-0,12224
-0,20911 -0,08909
-0,25895
5 let

31.

Klasické postupy
Teoretická i výpočetní jednoduchost,
Dobrá interpretovatelnost
Předpoklad : vnější podmínky,které determinují vývoj dané řady, mají být stabilní (princip
„ceteris paribus – za jinak stejných okolností“

32.

Adaptivní přístupy
Nepředpokládají
stabilitu analytického tvaru trendové funkce,
nepředpokládají ani spojitost trendové funkce.
A základě nově získaných údajů jsou modely plynule korigovány a
aktualizovány a mohou tak pracovat i s takovými složkami, jejichž
charakter se v čase výrazně nepravidelně mění.
Vycházejí z toho, že pro konstrukci prognózy budoucího vývoje jsou
nejcennější nejnovější pozorování.Těmto pozorováním jsou přiřazeny
nejvyšší váhy. Dřívějším pozorováním jsou přiřazeny váhy nižší, nebo
mohou být zcela vyřazeny.

33.

Nejužívanější – modely exponenciálního vyrovnání
Odhad trendu je získáván ve formě lineární kombinace všech
dosavadních pozorování řady, přičemž váhy dřívějších pozorování
exponenciálně klesají.
Holtův model
Brownův model
Wintersův model