Similar presentations:
Nelineární regresní funkce
1. Nelineární regresní funkce
2. Nelineární regrese
Na rozdíl od lineárních regresních modelů je třeba unelineárních modelů počítat s řadou komplikací:
neodhadnutelností některých parametrů,
existencí minima funkce jen pro některé regresní
modely,
výskytem lokálních minim a sedlových bodů,
špatnou podmíněností parametrů v regresním
modelu,
malým rozmezím experimentálních dat (zejména
u parametrů vyjadřujících limitní chování modelu).
3. Nelineární regrese
Funkce lineární v parametrechAditivní typy funkcí:
Kvadratická
Lomená
Logaritmická
Kubická
Funkce nelineární v parametrech
Multiplikativní typy funkcí:
Exponenciální
S - křivka
Mocninná
4. Funkce kvadratická (parabola)
y i a bxi cx2
i
150,0
y
100,0
Soustava normálních rovnic
an b xi c xi2 yi
a xi b xi2 c xi3 yi xi
a xi2 b xi3 c xi4 yi xi2
50,0
0,0
0,0
2,0
4,0
6,0
x
8,0
10,0
12,0
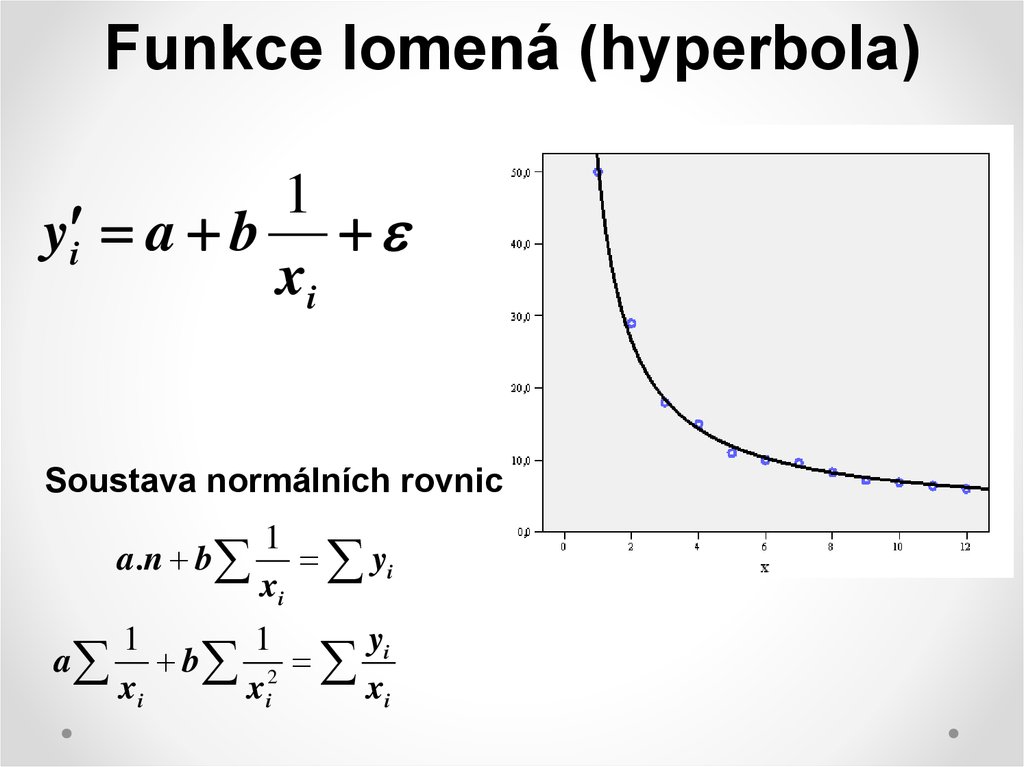
5. Funkce lomená (hyperbola)
1y i a b
xi
Soustava normálních rovnic
1
a .n b yi
xi
a
1
1
y
b 2 i
xi
xi
xi
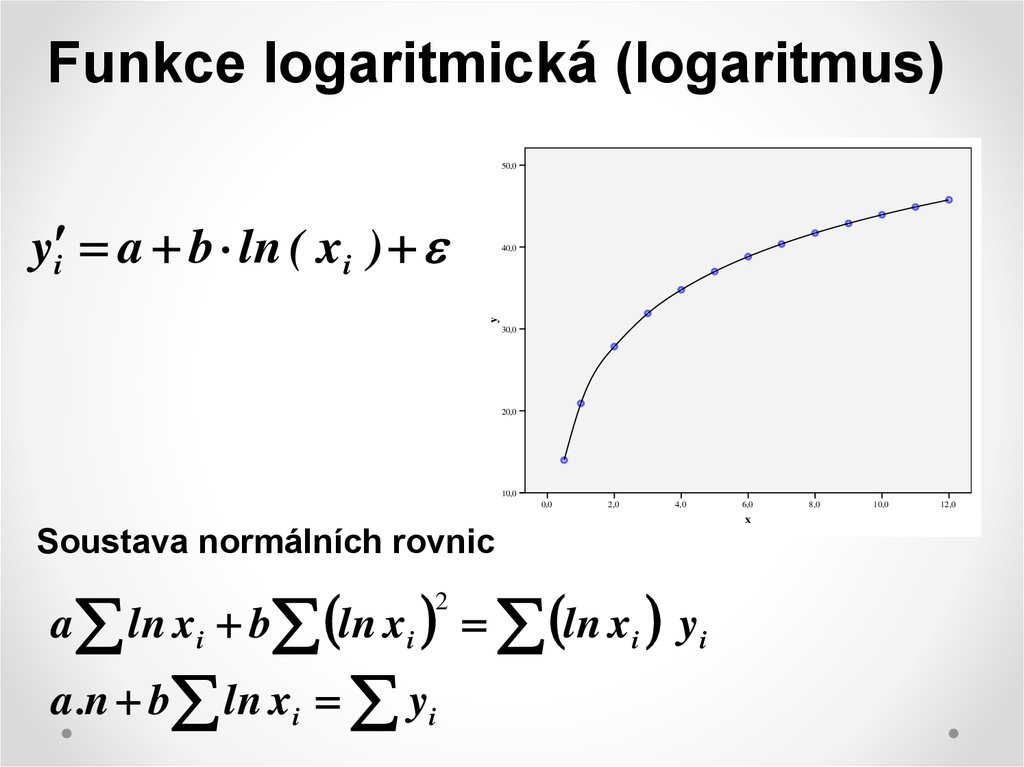
6. Funkce logaritmická (logaritmus)
50,0y i a b ln ( xi )
y
40,0
30,0
20,0
10,0
0,0
2,0
4,0
Soustava normálních rovnic
a ln xi b ln xi ln xi yi
2
a .n b ln xi yi
6,0
x
8,0
10,0
12,0
7. Funkce kubická
23
yi a bx i cx i dx i
8. Nelineární regrese
Jak již bylo uvedeno odhad parametrů u regresníchfunkcí, které nejsou lineární v parametrech,
neprovádíme MNČ přímo, protože její použití vede
k soustavě nelineárních rovnic, z nichž zpravidla
nedokážeme odhadnout přímo parametry ve formě
vhodných výpočetních vzorců.
Používá se tedy způsob, kdy určitou regresní funkci,
která je nelineární z hlediska parametrů, převedeme
pomocí linearizující transformace na funkci
lineární v parametrech.
9. Funkce mocninná
1 000,0800,0
y
y i ax ( e )
b
i
600,0
400,0
200,0
0,0
0,0
2,0
4,0
6,0
x
Soustava normálních rovnic
n . ln a b ln xi ln yi
lma ln xi b ln xi ln yi ln xi
2
8,0
10,0
12,0
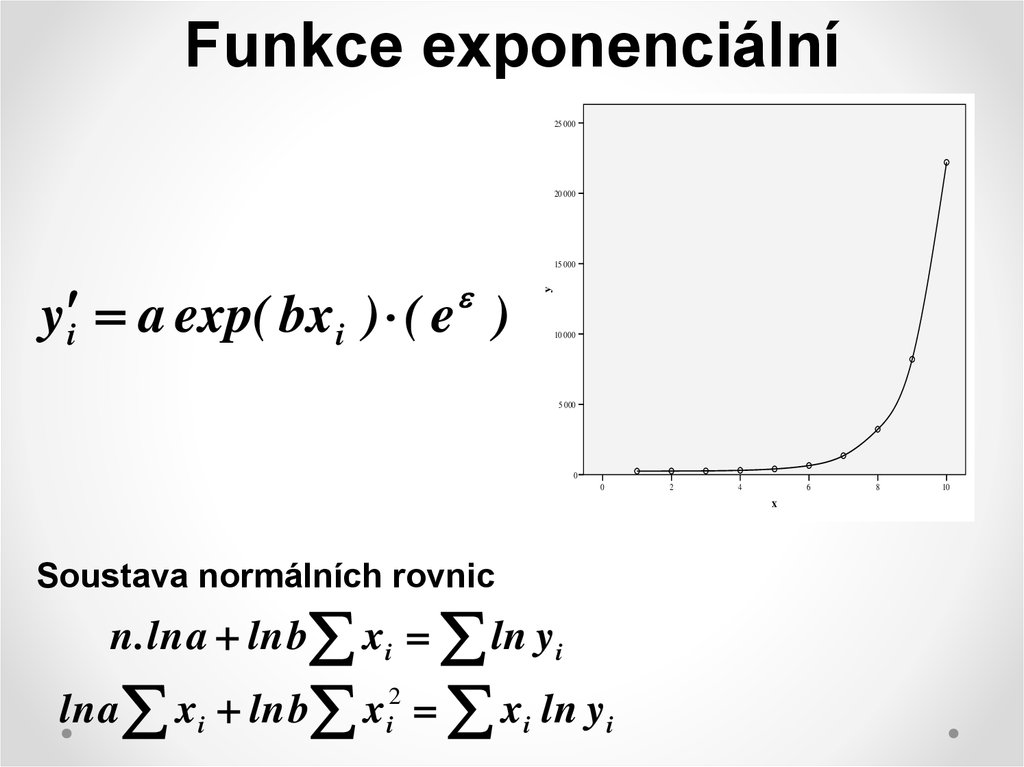
10. Funkce exponenciální
25 00020 000
yi a exp( bx i ) ( e )
y
15 000
10 000
5 000
0
0
2
4
6
x
Soustava normálních rovnic
n . ln a ln b xi ln yi
ln a xi ln b xi2 xi ln yi
8
10
11. Korelace při nelineární regresi
Při konstrukci míry ukazující na sílu závislostivycházíme ze vztahu empirických a vyrovnaných
hodnot.
( y i y ) ( yˆ i y ) ( y i yˆ i )
2
Sy
součet čtverců
odchylek y
2
=
ST
+
součet čtverců
vyrovnaných
hodnot
2
Sr
reziduální
součet čtverců
12. Korelace při nelineární regresi
Sílu závislosti je možné měřit index determinace.I
2
yx
ST
Sr
1
Sy
Sy
0 ≤ I2yx ≤ 1
Nízká hodnota indexu determinace nemusí ještě
znamenat nízký stupeň závislosti mezi proměnnými,
ale může signalizovat chybnou volbu regresní
funkce.
13. Korelace při nelineární regresi
Sílu závislosti je možné měřit index korelace.I yx I
2
yx
2
ˆ
( yi yi )
Sr
1
1
2
Sy
( yi y )
0 ≤ Iyx ≤ 1
I yx I xy
Index korelace se používá k měření těsnosti závislosti
pro libovolnou regresní funkci, jejíž parametry byly
odhadnuty metodou nejmenších čtverců. Má menší
vypovídací schopnost než index determinace.
14. Příklad
Ovlivňují investicích do reklamy výši tržeb ve firmě?Konstrukce regresního modelu
Proměnné:
x . . . investice do reklamy (v tis. Kč)
y . . . tržby z prodeje (v tis. Kč)
15. Příklad
Graf závislosti tržeb na výdajích (korelační pole)16. Příklad
Volba regresní funkce v SPSS17. Příklad
Hodnoty indexu determinace pro různé funkce18. Příklad
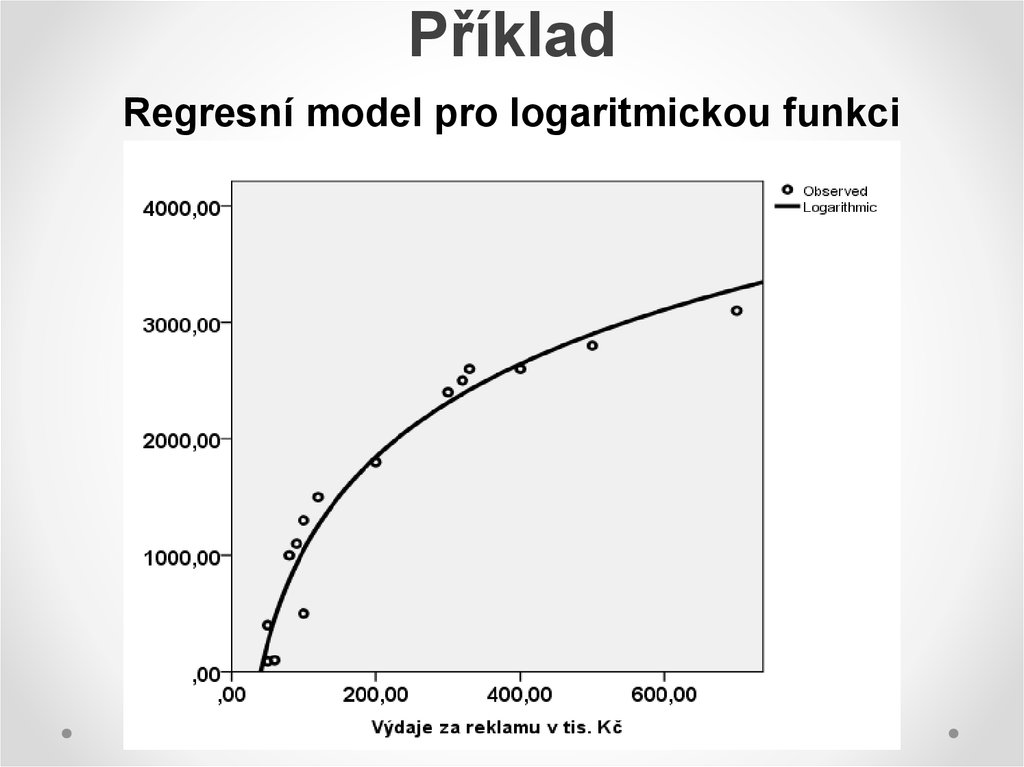
Volba logaritmického regresního modelu19. Příklad
Regresní model pro logaritmickou funkciIndex determinace část
rozptylu y, kterou lze
vysvětlit regresním
modelem
Opravená (adjustovaná)
hodnota penalizuje
regresní model za počet
parametrů
20. Příklad
Regresní model pro logaritmickou funkciTest regresního modelu
21. Příklad
Regresní model pro logaritmickou funkciParametry modelu
y i a b ln xi
y i 4 260 ,316 1151,988 ln xi


















 mathematics
mathematics








