Similar presentations:
Shrnutí minulé přednášky
1. Shrnutí minulé přednášky
Regresní analýza (průběh) – lineární regresní funkceBodové odhady a, b parametrů ,
se z pozorovaných dat nejčastěji získávají
metodou nejmenších čtverců.
x …..nezávisle proměnná
y …..závisle proměnná
, ..neznámé parametry v ZS
a, b ..neznámé parametry v VS
Korelační analýza (těsnost závislosti)
Populační korelační koeficient ρ
Výběrový korelační koeficient r
1 r 1
2. Testování regresních a korelačních charakteristik
3. Testování hypotéz
Podstatné testy významnosti v korelační aregresní analýze
● test významnosti korelačního koeficientu
● test významnosti jednotlivých regresních
parametrů
● test významnosti regresního modelu jako celku
4. Testování Pearsonova korelačního koeficientu
Hypotéza předpokládá, že korelace neexistuje,tzn. veličiny X a Y jsou nezávislé.
H0: = 0
Alternativní hypotéza je postavena na existenci
korelace.
H1: 0
5. Testování Pearsonova korelačního koeficientu
Test hypotézy se provádí pomocí testového kritériat
r
1 r
2
n 2,
V případě, že vypočtená hodnota testového kritéria
padne do kritického oboru, zamítá se nulová
hypotéza a existence lineární korelační závislosti
se považuje za prokázanou.
t t ( n 2 ) H0 se zamítá na
6. Testování Spearmanova koeficientu pořadové korelace
H0: s = 0H 1: s 0
Testování se provádí pomocí tabulek (tab. 22)
rS 0,73
> r0,05(9) = 0,602
< r0,01(9) = 0,735
Spearmanův korelační koeficient je statisticky
významný na 5% hladině významnosti.
7. Testování regresního koeficientu
Test významnosti nulové hypotézy vychází zeskutečnosti, že regresní koeficient je roven 0
(přímka nemá směrnici, je statisticky nevýznamná).
H 0: = 0
H 1: 0
8. Testování regresního koeficientu
Test hypotézy se provádí pomocí testového kritériat
b
sb
,
sb
2
sr
xi x
2
t t ( n 2 ) H0 se zamítá na
V případě, že se zamítá H0, je existence lineární
závislosti prokázána.
9. Test regresního modelu
Test významnosti celé regresní přímky (modelu)se provádí pomocí upravené jednoduché ANOVY.
V případě lineární regresní funkce je závěr testů
významnosti celého regresního modelu shodný
(ekvivalentní) s testem regresního koeficientu!!!
Pro rovnici s jedním prediktorem F = t2
10. Test regresního modelu
Testujeme nulovou hypotézu o nulovosti všechregresních koeficientů. H0: všechna b = 0
H1: non H0
S1
p 1
S1 ..
s12
Sr ..
Sr
2
sr
n p
F
Jestliže F > F zamítáme H0 na
2
s1
2
sr
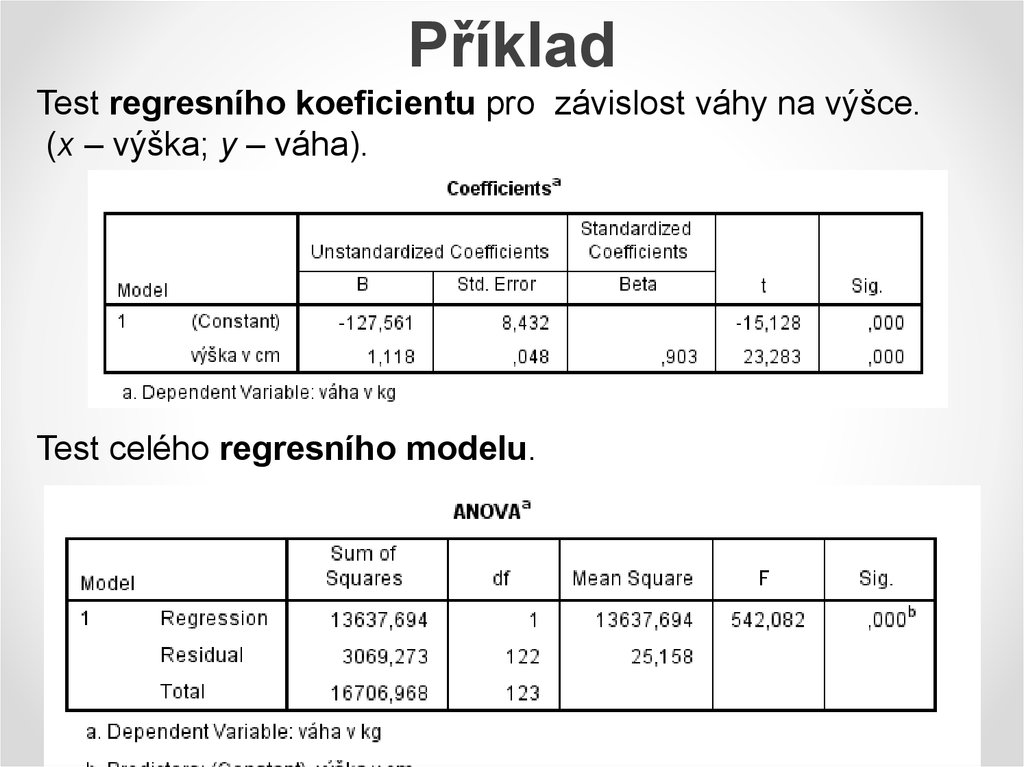
11. Příklad
Test regresního koeficientu pro závislost váhy na výšce.(x – výška; y – váha).
Test celého regresního modelu.
12. Odhad regresních a korelačních charakteristik
13. Korelační charakteristiky
Bodový odhad populačního korelačníhokoeficientu
n 1
ˆ 1 1 r
n 2
2
Intervalový odhad populačního korelačního
koeficientu
Postup výpočtu záleží na rozsahu výběrového souboru
14. Korelační charakteristiky
Intervalový odhad korelačního koeficientuV případě, že výběrový soubor má dostatečně
velký rozsah (n > 100), lze rozdělení výběrového
korelačního koeficientu aproximovat normálním
rozdělením.
Oboustranný interval spolehlivosti
P r u sr r u sr 1
1 r 2
sr
n
15. Korelační charakteristiky
Intervalový odhad korelačního koeficientuV případě, že výběrový soubor má rozsah n < 100,
provádíme Fisherovu Z- transformaci.
r Z a zpětně inverzní transformaci Z r
Oboustranný interval spolehlivosti pro Z
P ( Z u
1
, Z u
n 3
1
) 1
n 3
Převody hodnot provádíme pomocí tabulek.
16. Příklad
Intervalový odhad populačního korelačního koeficientu ρn = 15, r = 0,9322
Z – transformace (tab. 16.1) r = 0,9322 → Z = 1,6584
1
1
P ( 1,6584 1,96
;1,6584 1,96
) 1
15 3
15 3
P ( 1,0925 Z 2,2243) = 0,95
Zpětná (inverzní) transformace (tab. 16.2)
Z = 1,0925 → r = 0,7969
Z = 2,2243 → r = 0,9767
P ( 0,7969 ρ 0,9767) = 0,95
17. Regresní charakteristiky
Bodový odhad regresního koeficientu získávámepomocí metody nejmenších čtverců tzn.
b
Oboustranný interval spolehlivosti pro regresní
koeficient je vymezen následujícím vztahem
P b t ( n 2 ) s b t ( n 2 ) sb 1
sy 1 r 2
sr2
sb
2
( xi x ) s x n 2
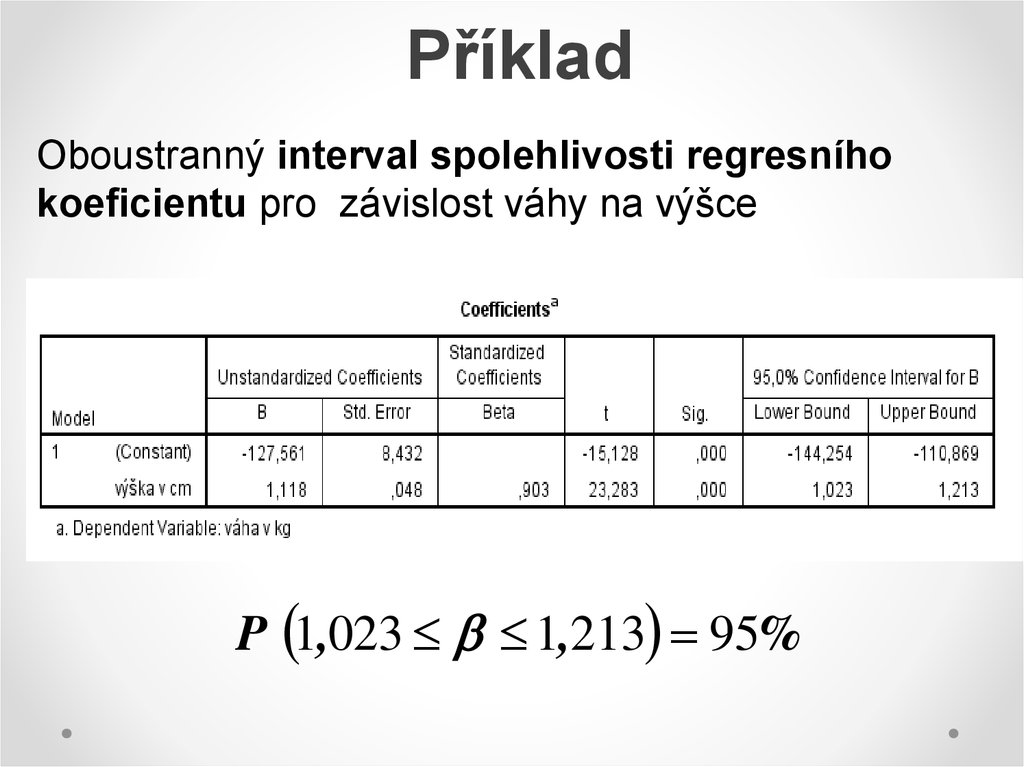
18. Příklad
Oboustranný interval spolehlivosti regresníhokoeficientu pro závislost váhy na výšce
P 1,023 1,213 95%
19. Regresní přímka
Výběrovou regresní přímku můžeme využít:1) Pro odhad podmíněné střední hodnoty závislé
veličiny y odpovídající určité konkrétní hodnotě
nezávislé veličiny xi.
Konfidenční pás pro přímku
2) Pro předpověď individuální hodnoty veličiny y´
odpovídající určité hodnotě nezávislé veličiny xi.
Predikční pás pro jednotlivá pozorování
20. Pásy spolehlivosti pro přímku
21. Shrnutí přednášky
Podstatou řešení regresní analýzy je:• stanovit nejvhodnější tvar regresního modelu
(tedy určit příslušnou rovnici, která bude
popisovat závislost y na x),
• stanovit jeho parametry (tj. stanovit konkrétní
hodnoty parametrů ),
• stanovit statistickou významnost parametru a
celého modelu (tj. zda model podstatným
způsobem přispěje ke zpřesnění odhadu závisle
proměnné),
• výsledky dané modelem interpretovat z hlediska
zadání.



















 mathematics
mathematics








