Základy statistiky

1.

Prezentace
pro 7. přednášku
6BZST1
Základy statistiky
doc. RNDr. Lenka Komárková, Ph.D.

2.

VÝSTUPY Z UČENÍ
Student bude:
schopen rozlišovat nezávislé a závislé
výběry
umět vybrat vhodný t-test
2
umět porovnat hodnoty populačních
průměrů dvou nezávislých i závislých
výběrů

3.

DVOUVÝBĚROVÉ TESTY
KVANTITATIVNÍ DATA

4.

DVOUVÝBĚROVÝ
t-TEST
Porovnání populačních průměrů dvou nezávislých výběrů
Oboustranný test
H0: μ1 = μ2
vs.
H1: μ1 ≠ μ2
vs.
vs.
H1: μ1 < μ2
H1: μ1 > μ2
H0: μ1 = μ2
H0: μ1 = μ2
4
Jednostranné testy

5.

DVOUVÝBĚROVÝ t-TEST
PŘEDPOKLADY
Nezávislé výběry (dvě různé skupiny)
Normální rozdělení obou výběrů
lze obejít přes velký počet dat v obou výběrech
Stejná variabilita dat (shoda rozptylů, homoskedasticita)
v obou výběrech
5
Pokud heteroskedasticita Welchova modifikace t-testu

6.

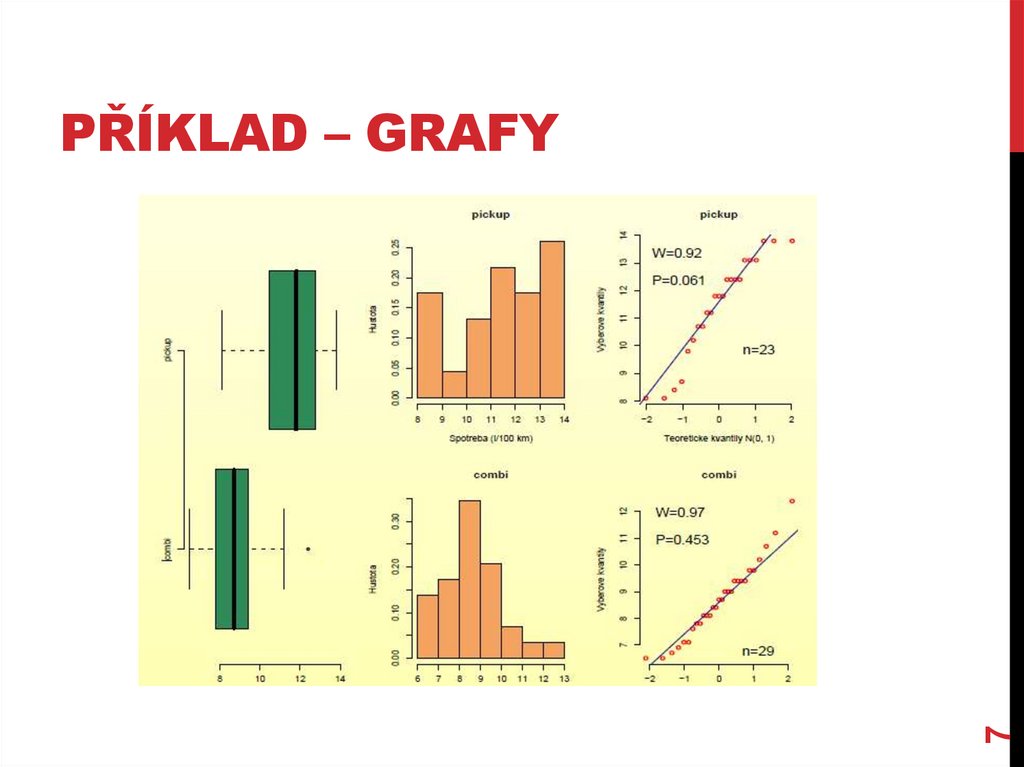
PŘÍKLAD
Je průměrná dálniční spotřeba pickupu jiná než průměrná dálniční
spotřeba combi auta?
H0: μ1 = μ2
vs.
H1: μ1 ≠ μ2
Je průměrná dálniční spotřeba pickupu vyšší než průměrná
dálniční spotřeba combi auta?
H0: μ1 = μ2
vs.
H1: μ1 > μ2
Je průměrná dálniční spotřeba pickupu o více jak 2 l/100 km vyšší
než průměrná dálniční spotřeba combi auta?
vs.
H1: μ1 > μ2 + 2
6
H0: μ1 = μ2 + 2

7.

7
PŘÍKLAD – GRAFY

8.

PŘÍKLAD I
Je průměrná dálniční spotřeba pickupu jiná než průměrná dálniční
spotřeba combi auta?
H0: μ1 = μ2
Výběrové průměry (směrodatné odchylky)
pickup: 11,426 (1,828)
vs.
combi: 8,662 (1,426)
Studentův t-test :
95% interval spolehlivosti:
T = 6,128
(1,858; 3,670)
p < 0,001
Welchův t-test :
95% interval spolehlivosti:
T = 5,955
(1,827; 3,702)
p < 0,001
vs.
H1: μ1 ≠ μ2
Na 5% hladině významnosti prokazujeme, že průměrná dálniční spotřeba
pickupu je jiná než průměrná dálniční spotřeba combi auta.
8

9.

PŘÍKLAD II
Je průměrná dálniční spotřeba pickupu vyšší než průměrná dálniční
spotřeba combi auta?
H0: μ1 = μ2
Výběrové průměry (směrodatné odchylky)
pickup: 11,426 (1,828)
vs.
combi: 8,662 (1,426)
Studentův t-test :
95% interval spolehlivosti:
T = 6,128
(2,008; +∞)
p < 0,001
Welchův t-test :
95% interval spolehlivosti:
T = 5,955
(1,983; +∞)
p < 0,001
vs.
H1: μ1 > μ2
Na 5% hladině významnosti prokazujeme, že průměrná dálniční spotřeba
pickupu je vyšší než průměrná dálniční spotřeba combi auta.
9

10.

PŘÍKLAD III
Je průměrná dálniční spotřeba pickupu o více jak 2 l/100 km vyšší
než průměrná dálniční spotřeba combi auta?
H0: μ1 = μ2 + 2
vs.
H1: μ1 > μ2 + 2
Výběrové průměry (směrodatné odchylky)
pickup: 11,426 (1,828)
vs.
combi: 8,662 (1,426)
Studentův t-test: T = 1,694
p = 0,048
95% interval spolehlivosti: (2,008; +∞)
Welchův t-test:
T = 1,646
95% interval spolehlivosti: (1,983; +∞)
p = 0,054
10
Studentův t-test má signifikantní výsledek na rozdíl od
Welchova t-testu.

11.

DVOUVÝBĚROVÝ
F-TEST (ORIENTAČNĚ)
Je směrodatná odchylka dálniční spotřeby pickupu stejná jako
směrodatná odchylka dálniční spotřeby combi auta?
H0: 1 = 2
vs.
H0: 12 = 22
vs.
H0: homoskedasticita
H1: 1 ≠ 2
H1: 12 ≠ 22
vs.
H1: heteroskedasticita
Výběrové směrodatné odchylky (rozptyly):
pickup: 1,828 (3,423) vs. combi: 1,426 (2,033)
Výsledek F-testu:
Interval spolehlivosti:
F = 1,644
(0,747; 3,764)
p = 0,214
11
Na 5% hladině významnosti nezamítáme homoskedasticitu
(shodu populačních rozptylů).

12.

DVOUVÝBĚROVÝ t-TEST
HOMOSKEDASTICITA
Je-li shodná variabilita, potom homoskedastický test má o něco
vyšší sílu než test heteroskedastický.
Postup, kdy nejprve F-testem zjistíme, jestli lze nebo nelze
předpokládat shodné rozptyly a poté se rozhodneme, zda použít
heteroskedastickou nebo homoskedastickou verzi t-testu, zvyšuje
pravděpodobnost chyby I. druhu nad povolené α.
Rozhodnutí o použitém testu by mělo být učiněno ještě předtím,
než máme data (např. historická zkušenost)
12
Není-li k tomu nějaký zvláštní důvod, provádíme v praxi obvykle
heteroskedastický t-test.

13.

DVOUVÝBĚROVÝ WILCOXONŮV
TEST (INFORMATIVNĚ)
Porovnání populačních mediánů dvou nezávislých výběrů
Neparametrická verze dvouvýběrového t-testu
místo pozorování se používají jejich pořadí
Předpoklady
Nezávislé výběry (dvě různé skupiny)
Spojité rozdělení obou výběrů (kvantitativní data v jednotlivých
výběrech by měly mít jen málo shod)
Stejná variabilita dat v obou výběrech
13
pokud není, pak je vhodnější Kolmogorovův-Smirnovův
test

14.

PÁROVÉ TESTY
KVANTITATIVNÍ DATA

15.

PÁROVÝ T-TEST
Porovnání populačních průměrů dvou závislých výběrů
Předpoklady
Závislé výběry (dvě měření u stejné skupiny)
Normální rozdělení rozdílu výběrů
(lze obejít přes velký počet dat)
15
jedná se vlastně o jednovýběrový t-test aplikovaný na
rozdílová data

16.

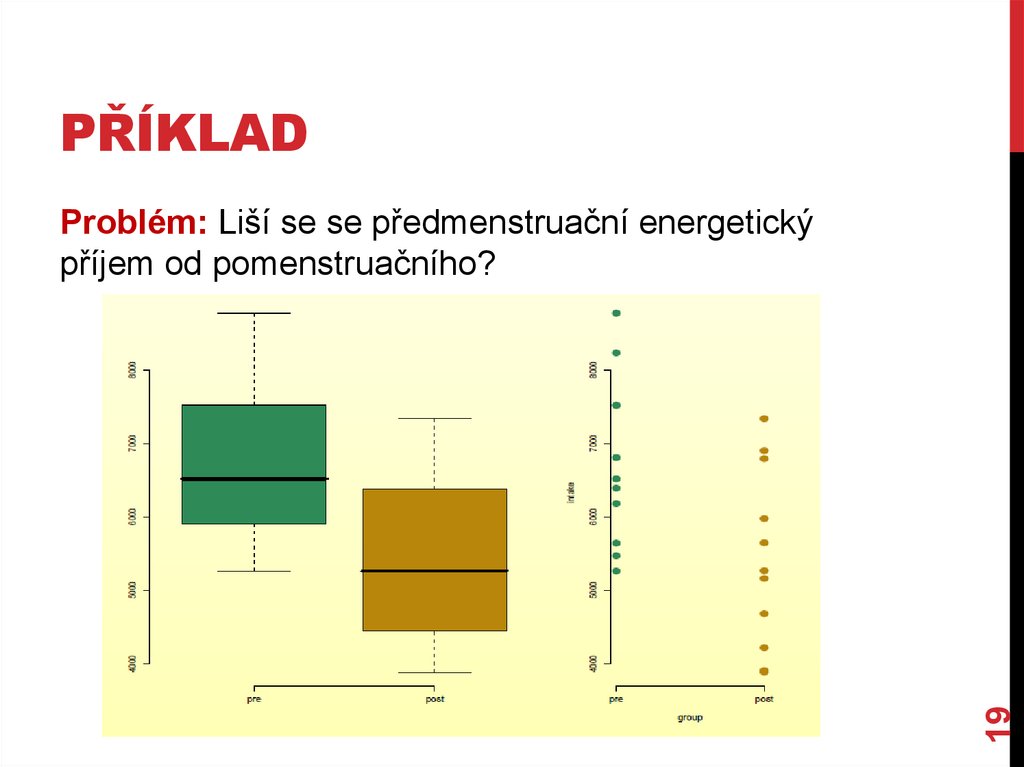
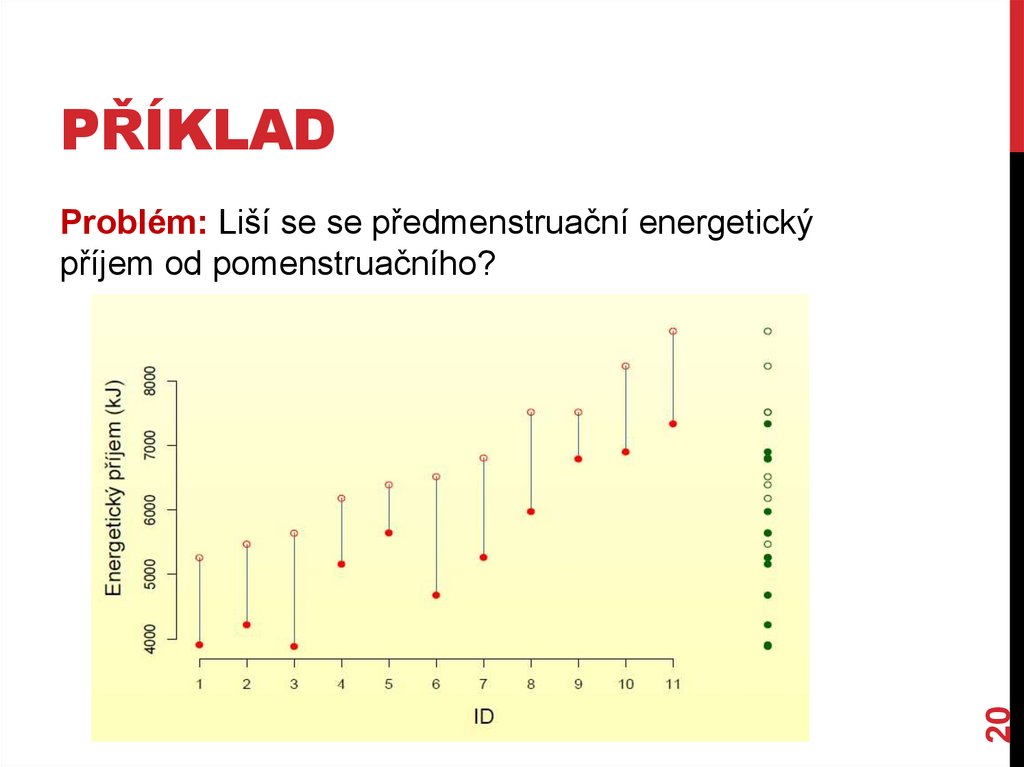
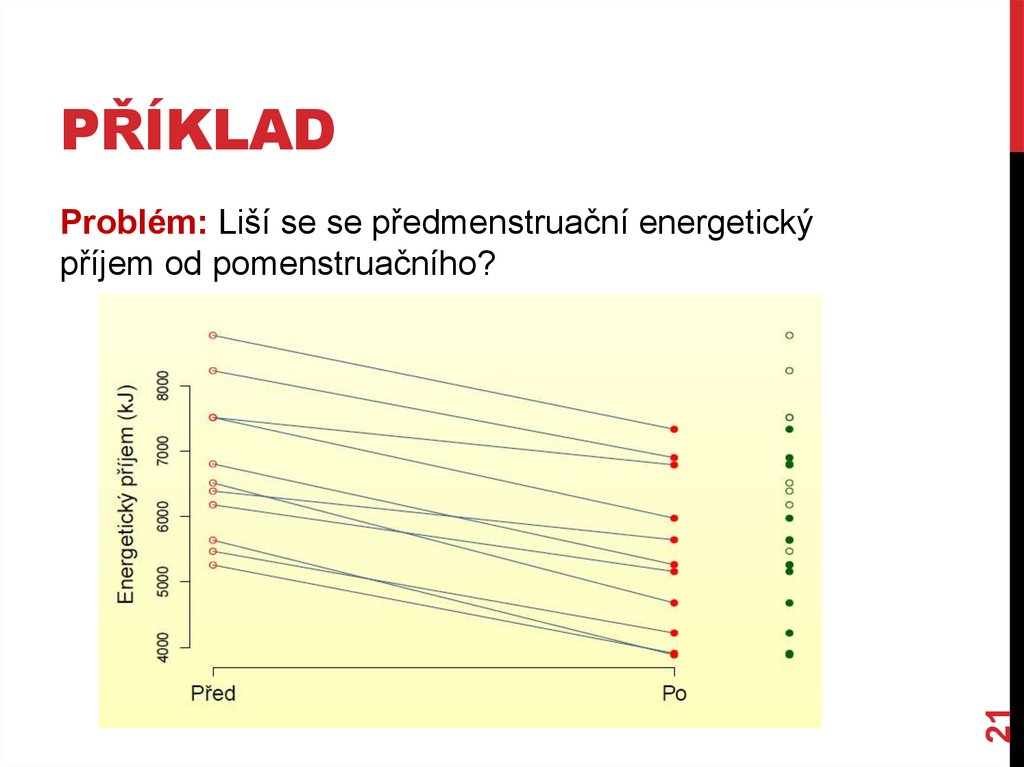
PŘÍKLAD
Problém: Liší se se předmenstruační energetický příjem od
pomenstruačního?
Dvouvýběrový přístup
Potřebujeme studii uskutečnit hned teď
Do studie zahrneme skupinu
n1 žen x dní před menstruací
n2 žen x dní po menstruaci
Charakteristiky jednotlivých žen jsou rušivými faktory při analýze
vlivu menstruace (faktor) na energetický příjem (odezva)
16
Zvyšuje se výběrová variabilita

17.

PŘÍKLAD
Problém: Liší se se předmenstruační energetický příjem od
pomenstruačního?
Párový přístup
Studii lze uskutečnit v období cca 1 měsíce
Do studie zahrneme skupinu n žen
Charakteristiky jednotlivých žen již nenaruší analýzu vlivu
menstruace (faktor) na energetický příjem (odezva)
17
Nižší výběrová variabilita než u dvouvýběrového přístupu

18.

PŘÍKLAD
Problém:
Liší se předmenstruační energetický příjem od pomenstruačního?
Denní energetický příjem v kJ (datový soubor anorekticky.xlsx)
ID
1
2
3
4
5
6
7
8
9
10
11
Před
5260
5470
5640
6180
6390
6515
6805
7515
7515
8230
8770
Po
3910
4220
3885
5160
5645
4680
5265
5975
6790
6900
7335
18
Zdroj dat: Altman, D.G. (1991). Practical Statistics for Medical Research. Chapman & Hall.

19.

PŘÍKLAD
19
Problém: Liší se se předmenstruační energetický
příjem od pomenstruačního?

20.

PŘÍKLAD
20
Problém: Liší se se předmenstruační energetický
příjem od pomenstruačního?

21.

PŘÍKLAD
21
Problém: Liší se se předmenstruační energetický
příjem od pomenstruačního?

22.

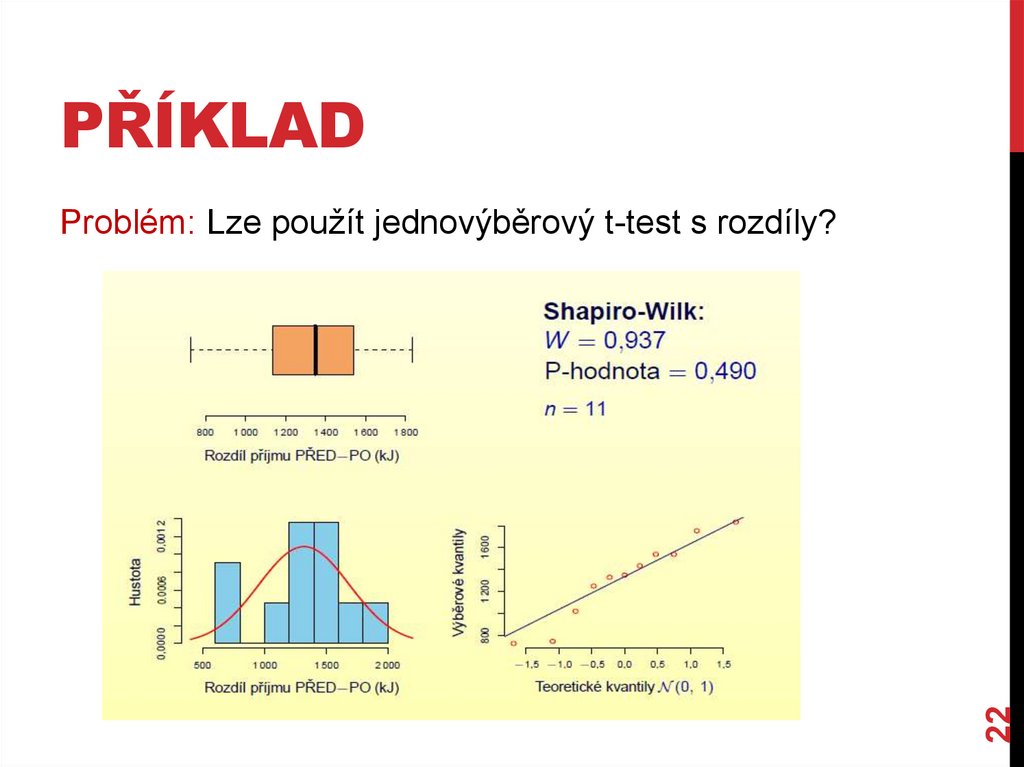
PŘÍKLAD
22
Problém: Lze použít jednovýběrový t-test s rozdíly?

23.

PŘÍKLAD
Liší se se předmenstruační energetický příjem od pomenstruačního?
H0: μ1 = μ2 H0: μ1 - μ2 = 0
H1: μ1 ≠ μ2 H1: μ1 - μ2 ≠ 0
Výsledek testu:
Testová statistika: 11,94
Dosažená hladina testu: p < 0,001
Na 5% hladině významnosti prokazujeme rozdíl mezi průměrným
předmenstruačním a pomenstruačním energetickým příjmem.
Interval spolehlivosti pro μ1 - μ2:
(1074,1; 1566,8)
S 95% spolehlivostí je předmenstruační energetický příjem v průměru
o nejméně 1 074,1 kJ a nejvýše o 1 566,8 kJ vyšší.
23

24.

VÝZNAM PÁROVÁNÍ
Eliminuje předem známé zdroje variability
(např. zdroj variability = anorektička)
Rozdíly se zjišťují nejprve uvnitř homogenní skupiny
(anorektička) a teprve potom se průměrují (jednovýběrový ttest)
24
Dvouvýběrový přístup ≡ nejprve průměruje zvlášť ve dvou
odlišných – heterogenních skupinách a teprve potom zjišťuje
rozdíly

25.

DVOUVÝBĚROVÝ
VS. PÁROVÝ TEST
nutné vždy vybrat správnou variantu testu!
(vyplývá většinou z povahy problému)
Příklady (který test vybrat?)
25
porovnání porodní hmotnosti narozených chlapců a děvčat
porovnání porodní hmotnosti narozených dvojčat
porovnání bazarových cen vozů ve dvou autobazarech
porovnání cen u stejných 100 výrobků v prodejně A a B
porovnání cen výrobků před slevou, a pak v době slevy

26.

PÁROVÝ
WILCOXONŮV TEST
Neparametrická verze párového t-testu
jedná se vlastně o jednovýběrový Wilcoxonův test
aplikovaný na rozdíly
Předpoklady
26
Závislé výběry
(dvě měření pro jednu skupinu, resp. dvě párová měření)
Spojité rozdělení rozdílu výběrů
(rozdílová data by měla mít jen málo shod)
Symetrie rozdělení rozdílu
(mírná asymetrie nevadí, pokud velká asymetrie, pak je
vhodnější znaménkový test)

27.

POSTUP V EXCELU
Dvouvýběrový Studentův t-test
Data Analýza dat Dvouvýběrový t-test s rovností
rozptylů
Dvouvýběrový Welchův t-test
Data Analýza dat Dvouvýběrový t-test s nerovností
rozptylů
Párový Studentův t-test
27
Data Analýza dat Dvouvýběrový párový t-test na
střední hodnotu

28.

TESTOVÁ OTÁZKA 1
Předpoklady dvouvýběrového Welchova t-testu jsou:
Vyberte libovolný počet možných odpovědí.
(Správná nemusí být žádná, ale také mohou být správné
všechny.)
a) homoskedasticita;
b) závislé výběry;
c) nezávislé výběry;
28
d) normální rozdělení.

29.

TESTOVÁ OTÁZKA 2
Jestliže chceme testovat shodu úrovně kvantitativního znaku ve
dvou odlišných skupinách a kvantitativní proměnná nesplňuje
předpoklady pro použití dvouvýběrového (Studentova či
Welchova) t-testu, možným použitelným testem v tomto případě
je:
Vyberte jen jednu z následujících možných odpovědí.
a) dvouvýběrový F-test o shodě rozptylů;
b) dvouvýběrový test o proporcích;
c) dvouvýběrový Wilcoxonův pořadový test;
29
d) párový Studentův test.

30.

KLÍČOVÁ SLOVA
Nezávislé výběry
Závislé výběry
Dvouvýběrový
Studentův t-test
Párování
Homoskedasticita
Dvouvýběrový
Wilcoxonův test
Dvouvýběrový
Welchův t-test
Párový Wilcoxonův test
30
Heteroskedasticita
Párový t-test

31.

LITERATURA
MAREŠ, Petr, RABUŠIC, Ladislav a SOUKUP, Petr. Analýza
sociálněvědních dat (nejen) v SPSS. 1. vydání. Brno:
Masarykova univerzita, 2015.
Kapitola 7.1 – 7.3.
HENDL, Jan. Přehled statistických metod: analýza a
metaanalýza dat. Páté, rozšířené vydání. Praha: Portál, 2015.
Kapitola 6.2.
31
MAREK, Luboš a kol. Statistika v příkladech. Druhé vydání.
Praha: Professional Publishing, 2015.
Kapitola 3.2.5.