Свойство квадратного корня

1.

МБОУ «Средняя общеобразовательная школа №2
им.Г.В.Кравченко »
y x
Учитель Каргаполова И.В.

2.

1 ; 2 ; 3 ; 4; …
множество натуральных чисел N
(2 N )
… - 4 ; -3 ; -2 ; -1; 0 ; 1 ; 2 ; 3 ; 4; … множество целых чисел Z
1
1 7
… - 4; -3,5;- 3; 2 ;- 2;- 1; 2 ; - 0; ; ; 1; 2; …
3
5 8
13
множество рациональных чисел Q
(2 Z )
(2 Q)
m
1 , поэтому
Любое целое число m можно записать в виде дроби
справедливо утверждение, что множество Q
рациональных чисел –
это множество, состоящее из чисел вида
натуральные числа) и числа 0
Q
N
Z
N Z
Z Q
m
m
;
(где m и n –
n
n
N подмножество множества Z

3.

5 = 5,0000… =0,5(0)
22
8,377= 8,3770000… =8,377(0)
7
0
7
0,3181818…= 0,3(18)
22
70
66
бесконечная десятичная
периодическая дробь
читаем: 0 целых 3 десятых
18 в периоде
0, 3 1 8 1 8 …
18 –это период
40 Опр.Повторяющаяся группа
22 цифр называется периодом
180
176
40
22
Вывод: любое рациональное число
можно записать в виде бесконечной
десятичной периодической дроби
Обратно: любую бесконечную
десятичную периодическую дробь
можно представить рациональным
числом.
180
176
…
717 1
16 15 8 5
2,1((77)) 22 2, (15
)2 2 2 2
9 90
90 99 45 33
112112
345
1 11 111115
101 37
2,12(12
,,11
(345
)(2 )2
)
2 2 2 22 2
900900
999 990333
900 330

4.

Задача. Площадь квадрата равна 16кв.см. Найти
сторону квадрата
x
x 16
x 4
2
2
x 25 x 5
x ?
x 5
2
2

5.

x 5
xx ?5 2,236...
2
Какоебесконечная
число надо десятичная
умножить само
на себя, чтобы
непериодическая
дробь
получить 5?
Опр. Бесконечная десятичная непериодическая дробь
называется иррациональным числом
Примеры:
10 ,
7,
5
1
3
иррациональные числа
рациональное число
25 5
5
-2
5
0,5
0
1
5
4
2
4
2
1
,
4
Опр. Рациональные и иррациональные числа образуют
класс действительных чисел R
3 1,7
5 2,2

6.

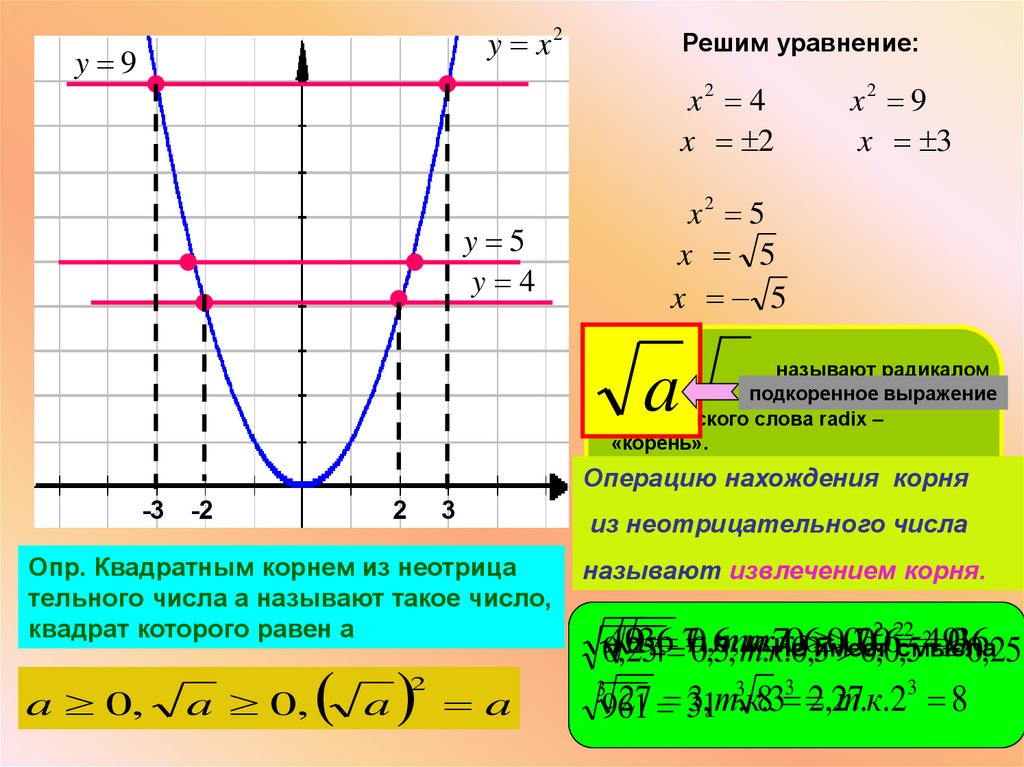
y x2
y 9
Решим уравнение:
x2 4
x 2
x2 9
x 3
x2 5
x 5
x 5
y 5
y 4
значок
называют радикалом
подкоренное выражение
от латинского слова radix –
«корень».
a
Операцию
нахождения
Само обозначение
корня корня
-3 -2
2
3
Опр. Квадратным корнем из неотрица
тельного числа а называют такое число,
квадрат которого равен а
a 0,
a 0,
a
2
a
напоминает
из неотрицательного числа
букву r, первую букву слова.
называют извлечением корня.
2 22 2
49
0
36
7
0
,
,
6
т
т
,
.
т
к
.
к
.
.
7
.
к
0
.
6
0
0
,
7
0
,
0
036
смысла
0,25
.0,имеет
5 0,,06
,5 49
0,25
4 0,5, т.кНе
3
3
3
27
3
,
т
.
к
8
.
3
2
,
27
т
.
к
.
2
8
961 31
3

7.

y x
х
у
0
0
1
4
1
2
y x
6,25 9
2,5
3
1.Область
определения
2. у=0
3.монотонность
4.ограниченность
5.наибольшее и
Наименьшее значения
6. непрерывность
Свойства
1.D( y) 0;
2. y 0 при x 0
3.Функция возрастает при x 0;
4. Функция ограничена снизу и
не ограничена сверху
5. yнаим 0, yнаиб нет
6. Функция непрерывна
7. Функция выпукла вверх

8.

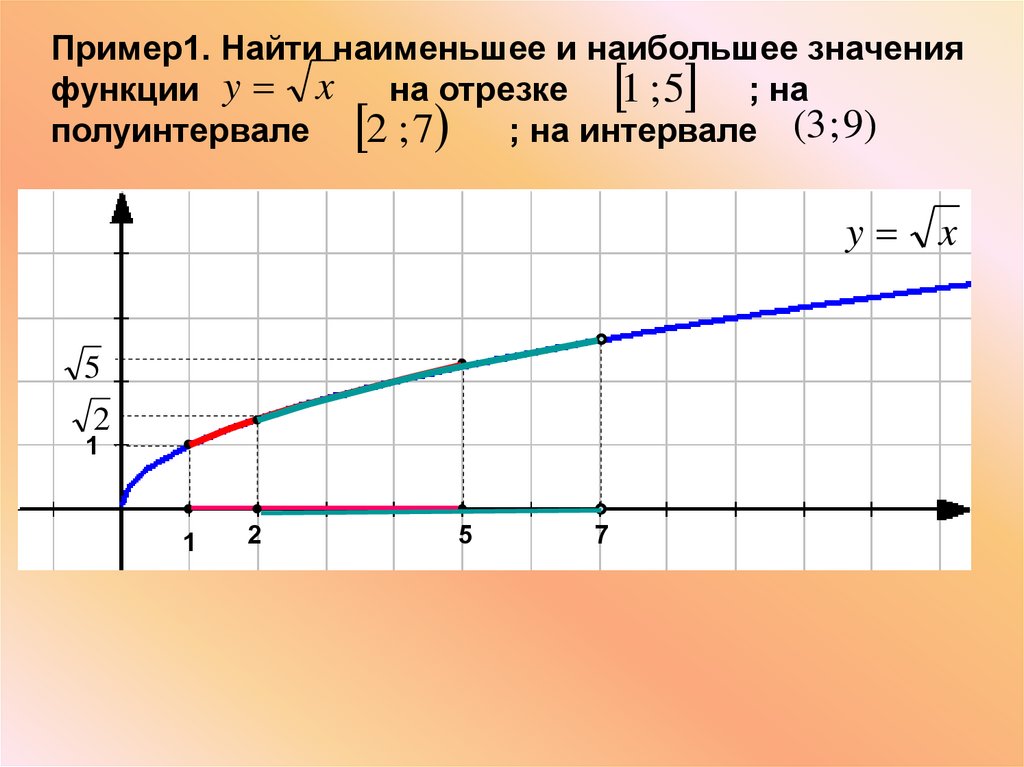
Пример1. Найти наименьшее и наибольшее значения
функции y x
на отрезке
; на
1 ;5
2 ;7
полуинтервале
; на интервале (3 ; 9)
y
5
2
1
1
2
5
7
x

9.

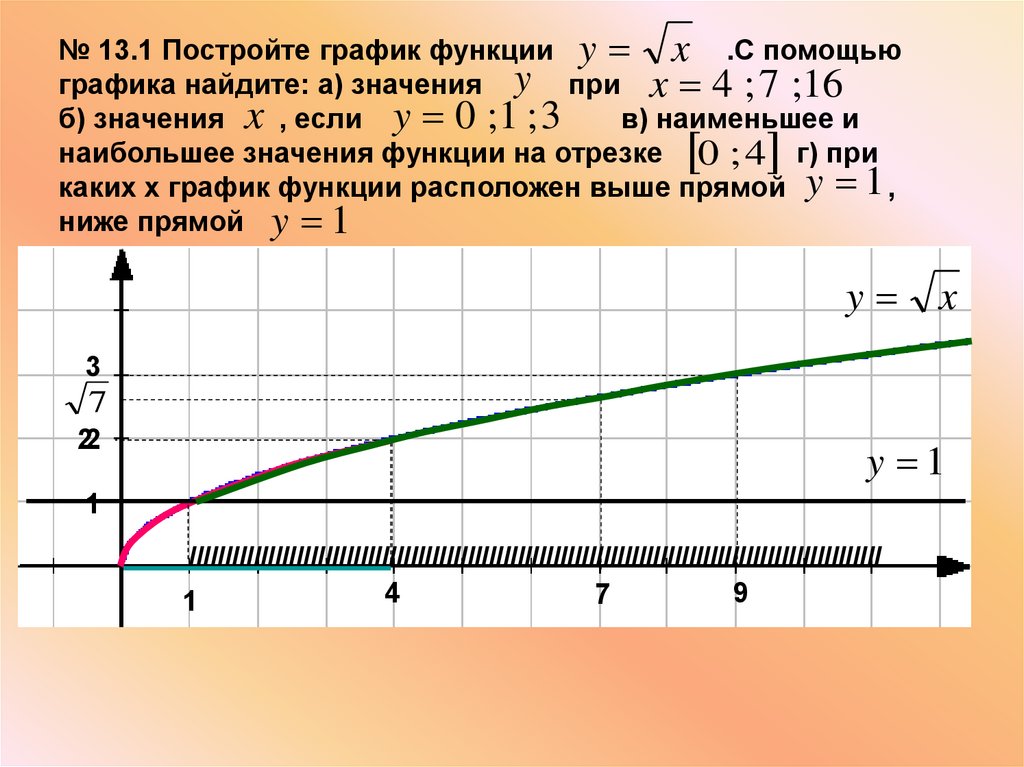
№ 13.1 Постройте график функции y x .С помощью
графика найдите: а) значения y при x 4 ; 7 ;16
б) значения x , если y 0 ;1 ; 3
в) наименьшее и
наибольшее значения функции на отрезке 0 ; 4 г) при
каких х график функции расположен выше прямой y 1 ,
ниже прямой y 1
y
x
3
7
22
y 1
1
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
1
4
7
9

10.

Построить графики функций
y
1. y x 4
O(0;0) O (4;0)
2. y x 2 3
y
O(0;0) O ( 2; 3)
x
x