Similar presentations:
Тригонометрические уравнения - равносильные преобразования
1. «Тригонометрические уравнения - равносильные преобразования»
«ТРИГОНОМЕТРИЧЕСКИЕУРАВНЕНИЯ
-
РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ»
Ю.В.Терешина – учитель
I квалификационной категории
2. Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен
МАТЕМАТИКУ НЕЛЬЗЯ ИЗУЧАТЬ,НАБЛЮДАЯ, КАК ЭТО ДЕЛАЕТ СОСЕД!
А. НИВЕН
3.
Свойства основных тригонометрических функцийy sin x
y cos x
Область
определения
;
Множество
значений
y tgx
y ctgx
;
k ; k
2
2
k; k
1;1
1;1
;
;
Четность
нечетная
четная
нечетная
нечетная
Периодичность
(основной
период)
2
2
4.
Простейшие тригонометрические уравненияsin x a
Если a 1 , то
уравнение не имеет
корней
a 1 , то
Если
x 1 arcsin a n,
n
n Z
5.
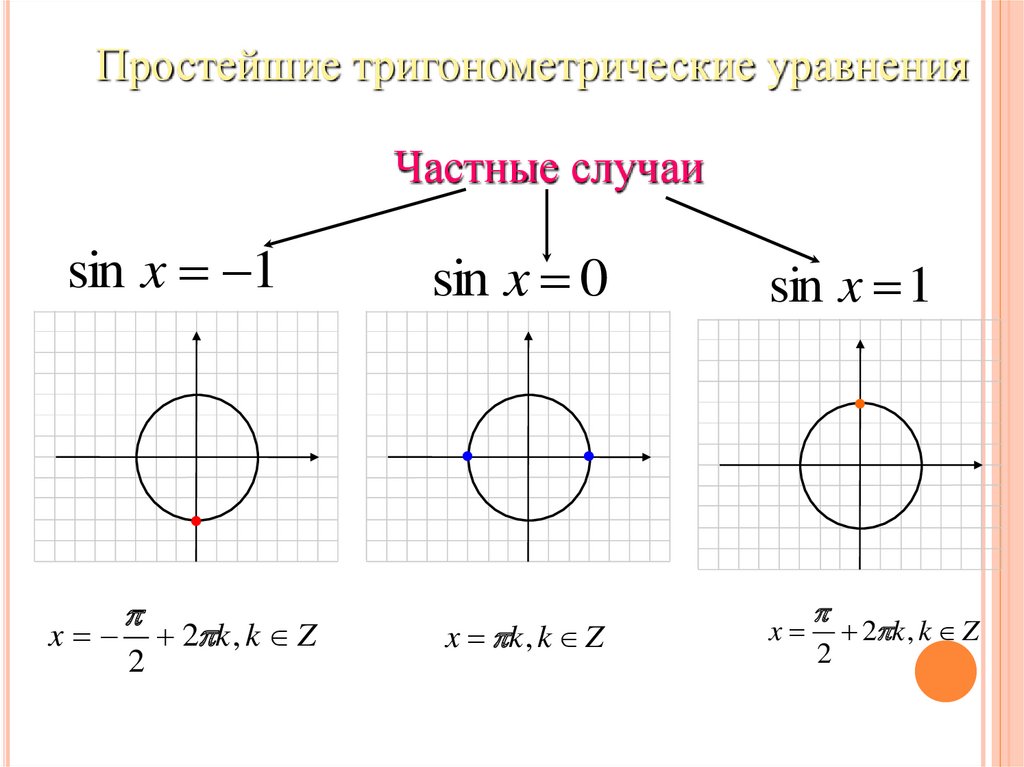
Простейшие тригонометрические уравненияЧастные случаи
sin x 1
x
2
2 k , k Z
sin x 0
x k , k Z
sin x 1
x
2
2 k , k Z
6.
Простейшие тригонометрические уравненияcos x a
Если a 1 , то
уравнение не имеет
корней
Если
a 1 , то
x arccos a 2 n,
n Z
7.
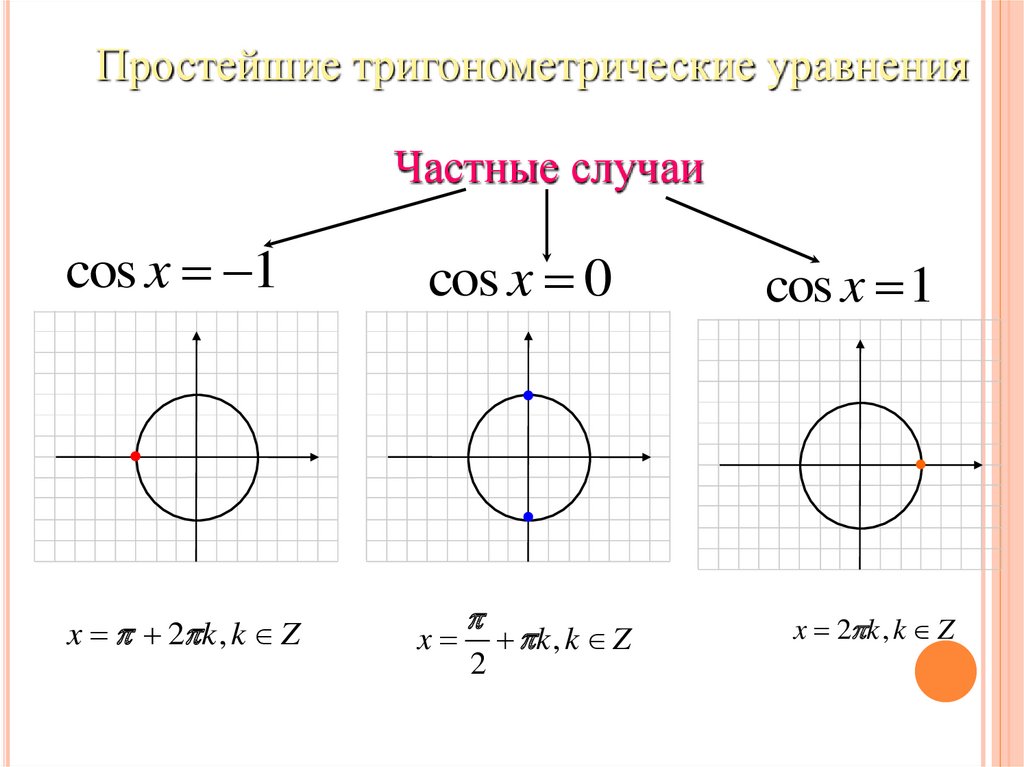
Простейшие тригонометрические уравненияЧастные случаи
cos x 1
x 2 k , k Z
cos x 0
x
2
k , k Z
cos x 1
x 2 k , k Z
8.
Простейшие тригонометрические уравненияtgx a
x arctga n, n Z
ctgx a
x arcctga n, n Z
9. Задание 1.
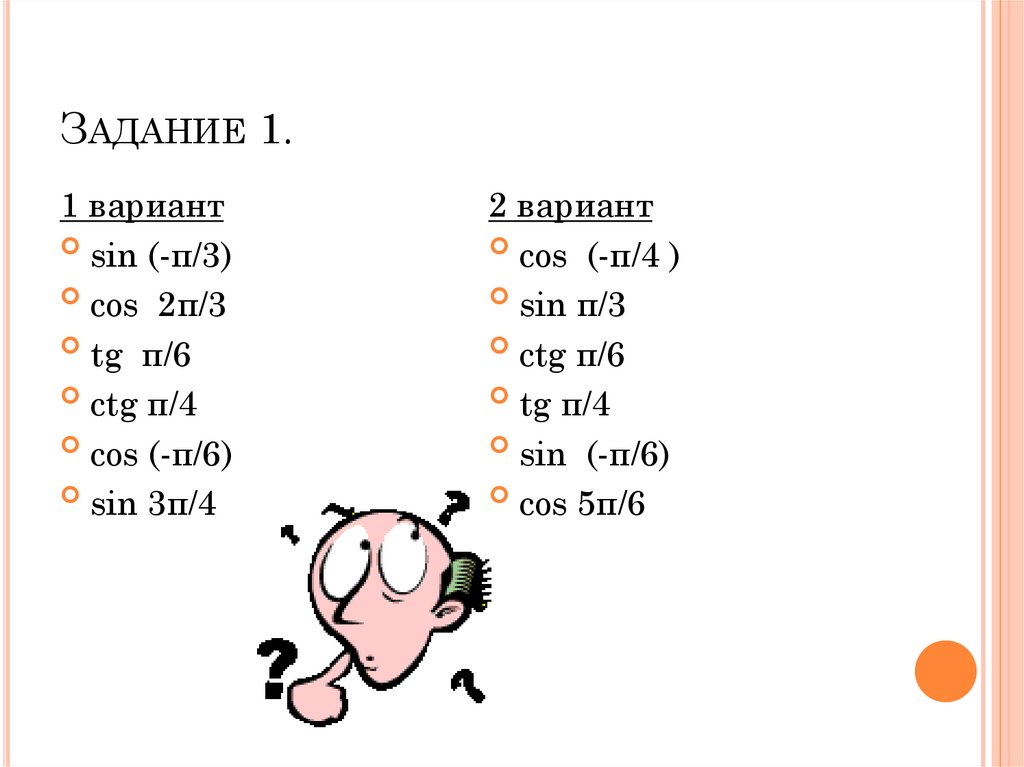
ЗАДАНИЕ 1.1 вариант
sin (-π/3)
cos 2π/3
tg π/6
ctg π/4
cos (-π/6)
sin 3π/4
2 вариант
cos (-π/4 )
sin π/3
ctg π/6
tg π/4
sin (-π/6)
cos 5π/6
10. Задание 2.
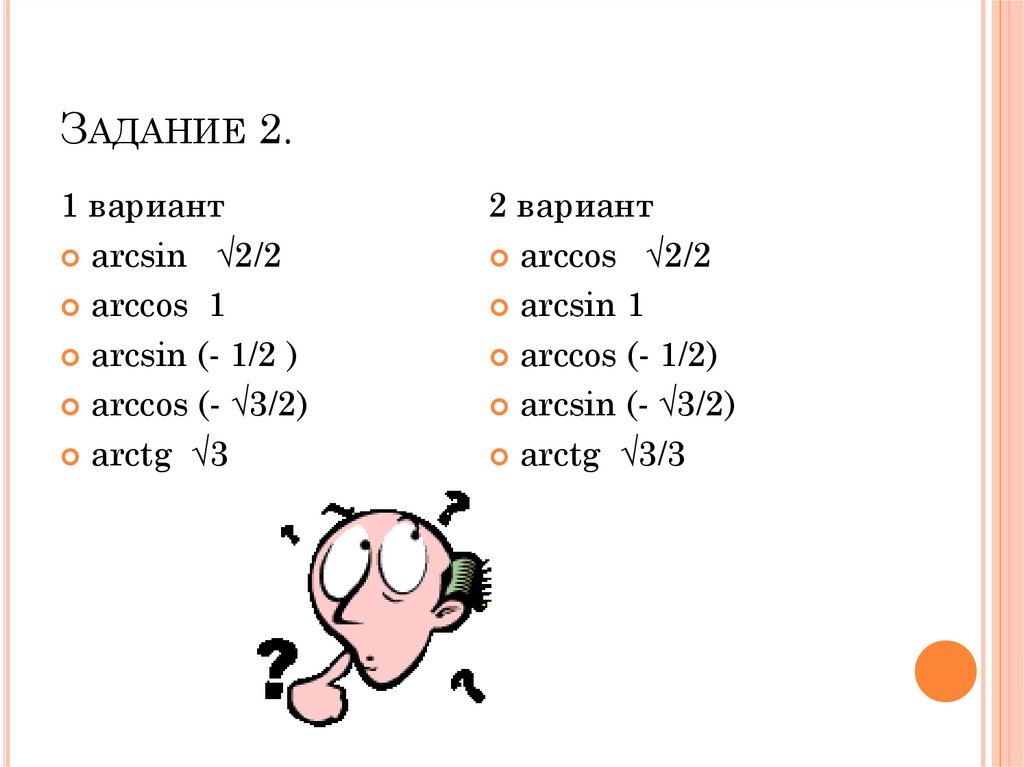
ЗАДАНИЕ 2.1 вариант
arcsin √2/2
arccos 1
arcsin (- 1/2 )
arccos (- √3/2)
arctg √3
2 вариант
arccos √2/2
arcsin 1
arccos (- 1/2)
arcsin (- √3/2)
arctg √3/3
11. Задание 3.
ЗАДАНИЕ 3.Вариант1
Вариант 2
1
1
2
2
3
3
12.
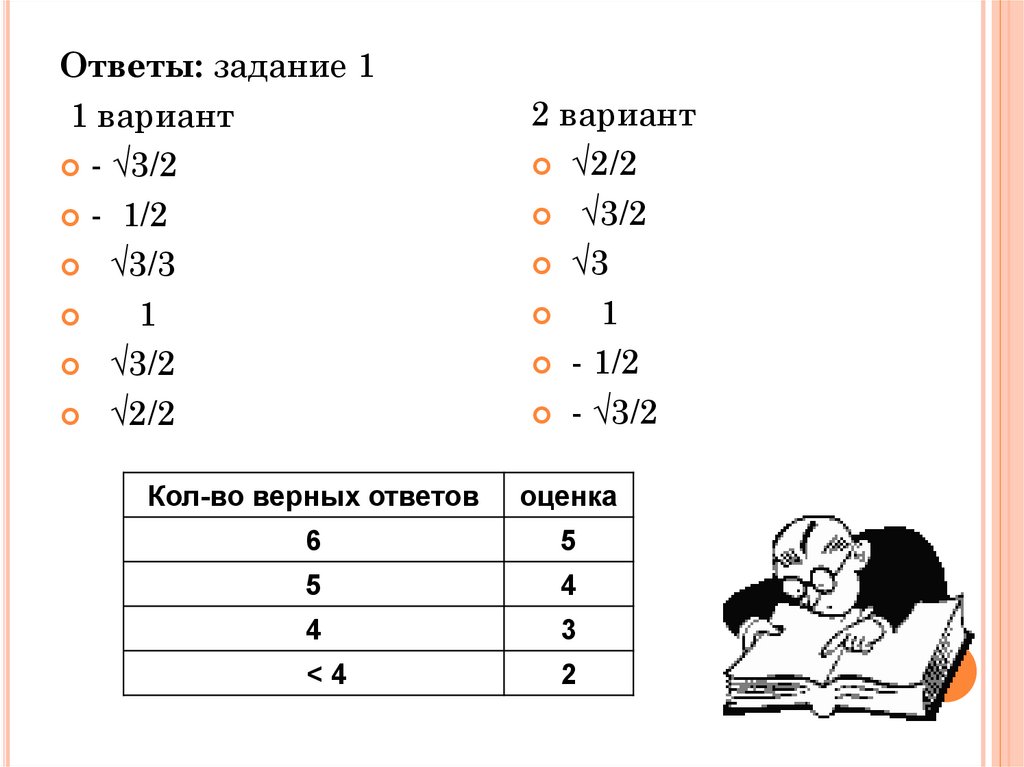
Ответы: задание 11 вариант
- √3/2
- 1/2
√3/3
1
√3/2
√2/2
2 вариант
√2/2
√3/2
√3
1
- 1/2
- √3/2
Кол-во верных ответов
оценка
6
5
5
4
4
3
<4
2
13.
Ответы : задание 21 вариант
π/4
0
- π/6
5π/6
π/3
2 вариант
π/4
π/2
2π/3
- π/3
π/6
Кол-во верных ответов
оценка
5
5
4
4
3
3
<3
2
14.
Ответы : задание 31 вариант
2
2
-3
2 вариант
-8
3
4
Кол-во верных ответов
оценка
3
5
2
4
1
3
0
2
15. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ - РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
Если совпадают МНОЖЕСТВА всех корней этих уравнений16.
2sin2x+3cos2x−2=0 2sin2x+3 1−sin2x −2=02sin2x+3sinx−2=0 2y2+3y−2=0
sin2x−3cosx=0 2sinxcosx−3cosx=0
Приведение
тригонометрических
cos2x=1−sin2x
выражений к одному виду
Замена функции новой
переменной
sinx=y
Приведение
тригонометрических
sin2x=2sinxcosx
выражений к одинаковому
углу
17.
1 Перенос члена уравнения sin2x + 3 = 4 sin2x =1(c
противоположным
знаком) из одной части
уравнения в другую
2 Умножение
(деление) 2 sin2x=1,
обеих частей на отличное
от нуля число
0
3 Применение
справедливых
каждого x R
тождеств,
для
18. Рассмотрим некоторые равносильные преобразования которые используются при решении уравнений
РАССМОТРИМ НЕКОТОРЫЕ РАВНОСИЛЬНЫЕПРЕОБРАЗОВАНИЯ КОТОРЫЕ ИСПОЛЬЗУЮТСЯ ПРИ
РЕШЕНИИ УРАВНЕНИЙ
19.
82
sin x
2
2
cos x
0
20.
http://shpargalkaege.ru/c1reshnew/c1resh8/c1resh8.html21.
22.
Правильному применению методовможно научиться только применяя их
на разнообразных примерах.
(Г. Цейтен)













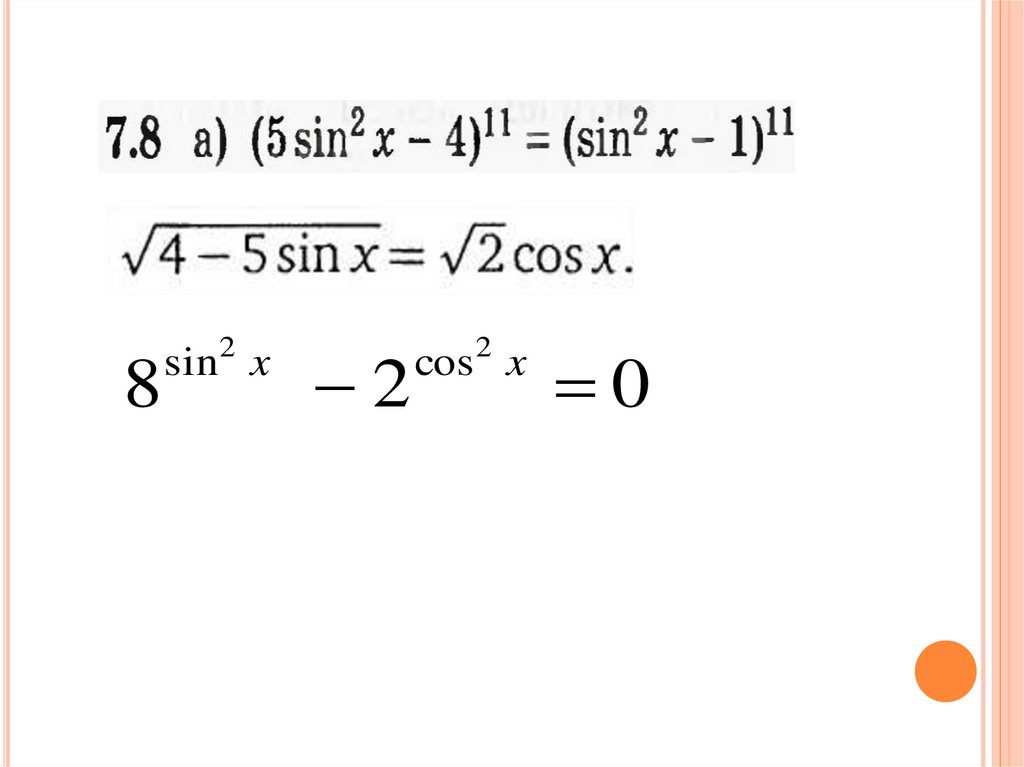



 mathematics
mathematics








