Similar presentations:
Типы тригонометрических уравнений
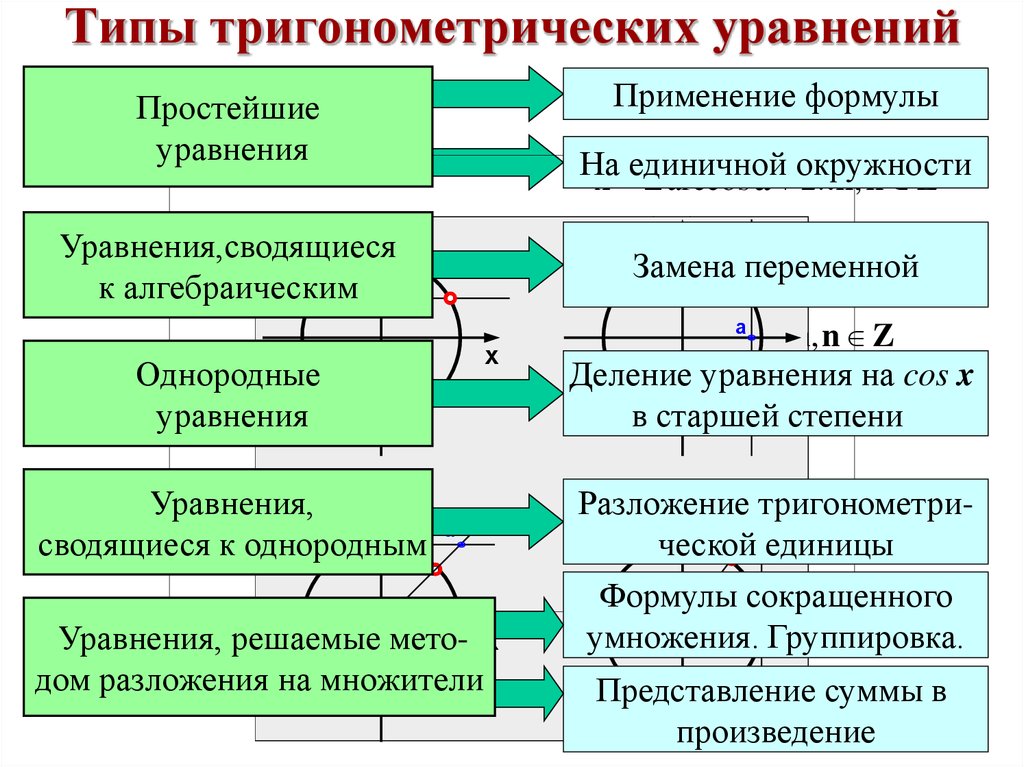
1. Типы тригонометрических уравнений
Применение формулыПростейшие
уравнения
На
x единичной
arccos a окружности
2 n, n Z
sin x=a
Уравнения,сводящиеся
к алгебраическим a
x x=a
y1 arcsin a n, n Z
cos
Замена переменной
x arctg a n, n Z
Однородные
уравнения
x arcctg aa n, n Z
x
Деление уравнения на cos x
в старшей степени
n
y
Уравнения, y
ctg x=a
сводящиеся к однородным
x
a
Уравнения, решаемые мето- x
дом разложения на множители
Разложение
тригонометриy
a
tg x=a
ческой единицы
Формулы сокращенного
умножения. Группировка.
x
Представление суммы в
произведение
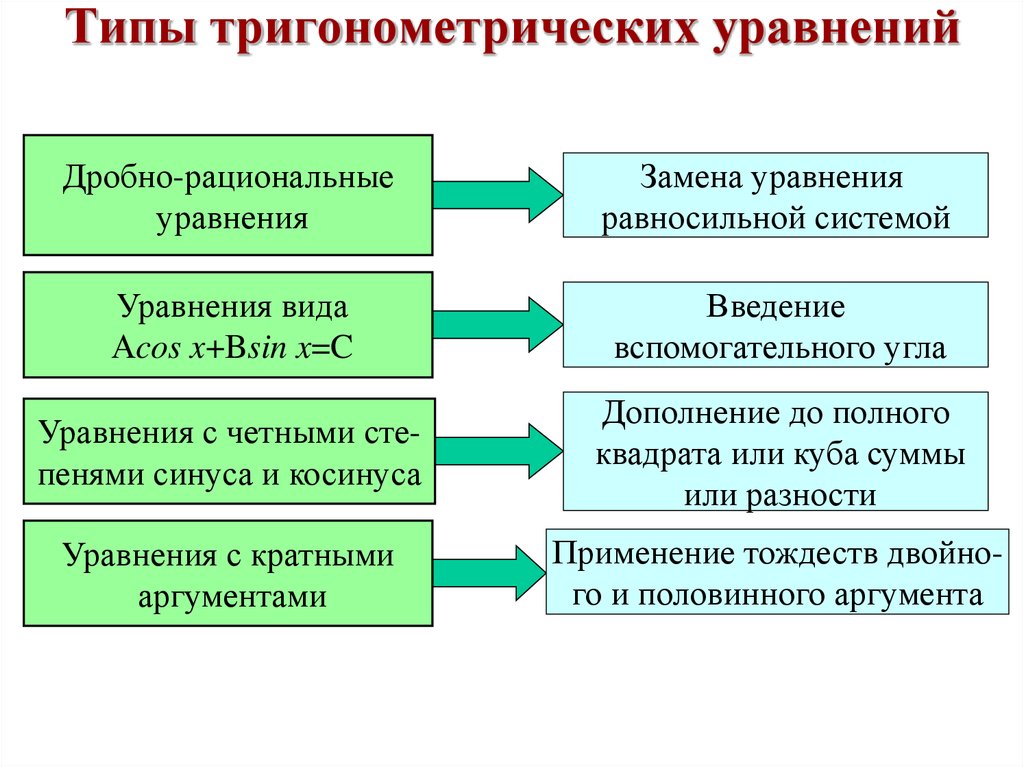
2. Типы тригонометрических уравнений
Дробно-рациональныеуравнения
Замена уравнения
равносильной системой
Уравнения вида
Аcos x+Bsin x=C
Введение
вспомогательного угла
Уравнения с четными степенями синуса и косинуса
Дополнение до полного
квадрата или куба суммы
или разности
Уравнения с кратными
аргументами
Применение тождеств двойного и половинного аргумента
3. Решить уравнение
1 способ (по формуле)1
1 ) cos x
3
2
1
x arccos 2 n, n Z,
3
2
2 способ (на единичной окружности)
x
2 n, n Z, или
3
3
x
2 n, n Z;
3
3
x 2 n , n Z ,
3
3
x 2 n , n Z.
3 3
у
x
x 2 n, n Z, или
2
2 n, n Z.
3
2
Ответ : 2 n;
2 n, n Z.
3
x
4. Решить уравнение
2) sin2x + 5sinx – 6 = 0Введем новую переменную t = sinx,
t2 - 5t – 6 = 0;
t1 = 1;
sinx = 1;
t2 = -6;
sinx = -6;
x = 2 n, n Z.
2
нет решений, т.к. sinx 1
Ответ: 2 n , n Z .
2
3) 3cos2x – sinx – 1 = 0
Замена синуса на косинус с помощью тождества cos 2x = 1 - sin 2x;
3(1 - sin2x) – sinx – 1 = 0;
3 - 3sin2x – sinx – 1 = 0;
3sin2x + sinx + 2 = 0;
5. Решить уравнение
4) sin(x - ) - cos(x - ) = 03
3
Разделим обе части уравнения на cos(x Деление возможно, т. к. cos(x tg(x - ) - 1= 0;
3
tg(x - ) = 1;
3
x - = n, n Z ;
4
3
n, n Z .
12
Ответ: n, n Z .
12
x=
)
3
).
3
= 0 не является корнем уравнения.
6. Решить уравнение
5) 2sin2x - 5sinxcosx - cos2x = -2Применим тригонометрическое разложение единицы 1=sin2x + cos2x
2sin2x - 5sinxcosx - 8cos2x = -2(sin2x+cos2x);
2sin2x - 5sinxcosx - 8cos2x+2sin2x+2cos2x = 0;
4sin2x - 5sinxcosx - 6 cos2x = 0;
Делим уравнение почленно на cos2x. (Почему деление возможно?)
4tg2x - 5tgx – 6 = 0;
7. Решить уравнение
6) 2sin2x + sin2x = 0Применим формулу синуса двойного угла sin2x = 2sinxcosx
2sinx + 2sinxcosx = 0;
2sinx(sinx + cosx) = 0;
Применим свойство произведения
sinx = 0 или sinx + cosx = 0;
8. Типы тригонометрических уравнений
Проверочная работа1 вариант
2 вариант
-4
1) 2sin2x = 1;
1) cos(x
2) 2sin2x – 5cosx + 1 = 0;
2) 2 cos2x + 3sinx = 0;
3) sin2x - sinx cosx - 3cos2x = 0;
3) sin3x- 3cos3x = 0;
4) cos4x + cos2x = 0;
4) sin3x + sin5x + sin4x = 0;
5) 6 sin2x + 1,5sin2x = 0;
5) cos2x + sin2x = 0;
) = 1;






 mathematics
mathematics








