Similar presentations:
Тригонометрические уравнения
1.
Тригонометрическиеуравнения
2.
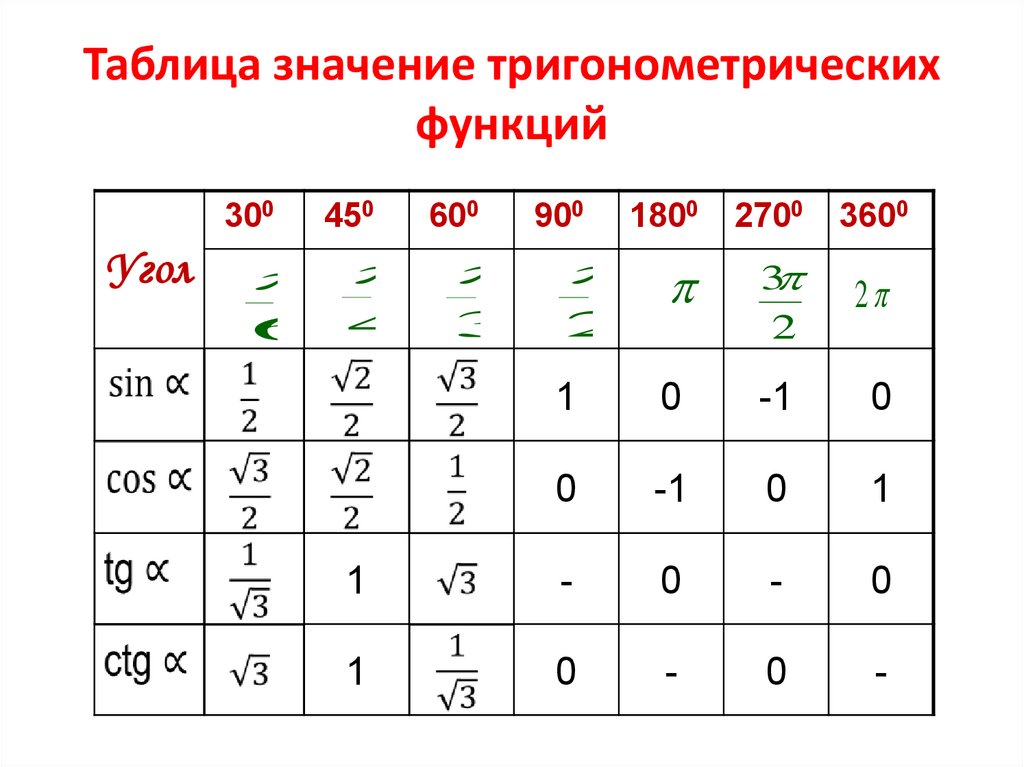
Таблица значение тригонометрическихфункций
300
Угол
450
600
900
1800
6 4 3
2
2700
3600
3
2
2
1
0
-1
0
0
-1
0
1
1
-
0
-
0
1
0
-
0
-
3.
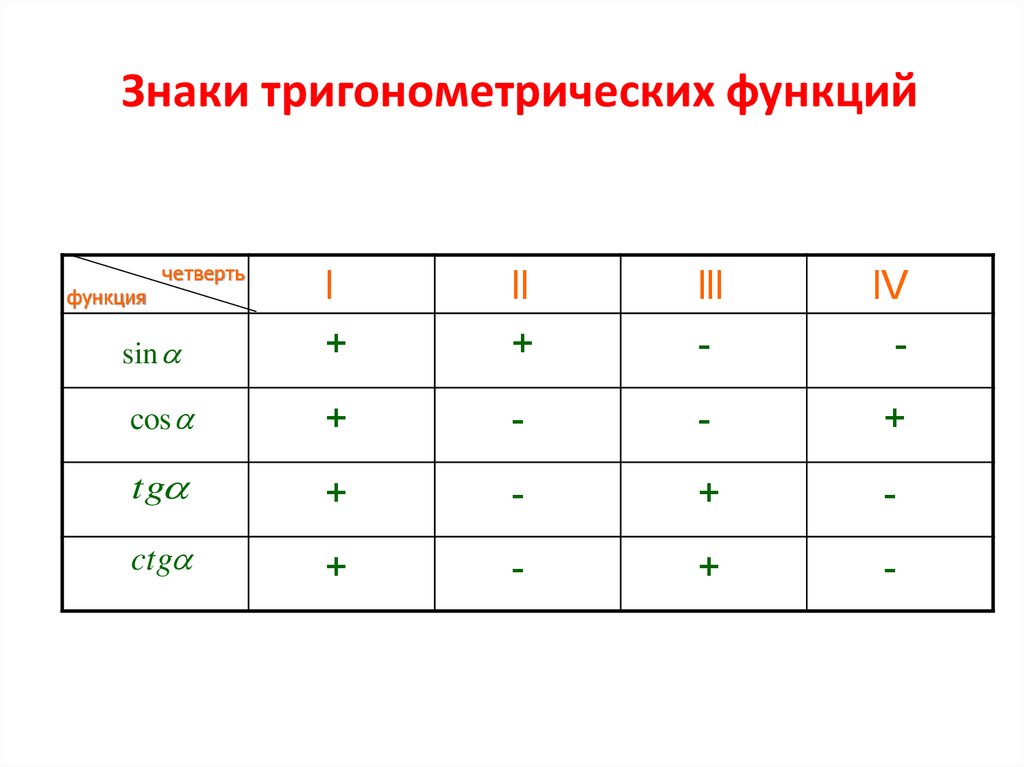
Знаки тригонометрических функцийчетверть
sin
l
+
ll
+
lll
-
lV
-
cos
+
-
-
+
tg
+
-
+
-
ctg
+
-
+
-
функция
4.
Синус, косинус, тангенс и котангенсуглов α и -α
sin( ) sin
cos( ) cos
tg( ) tg
ctg ( ) ctg
5.
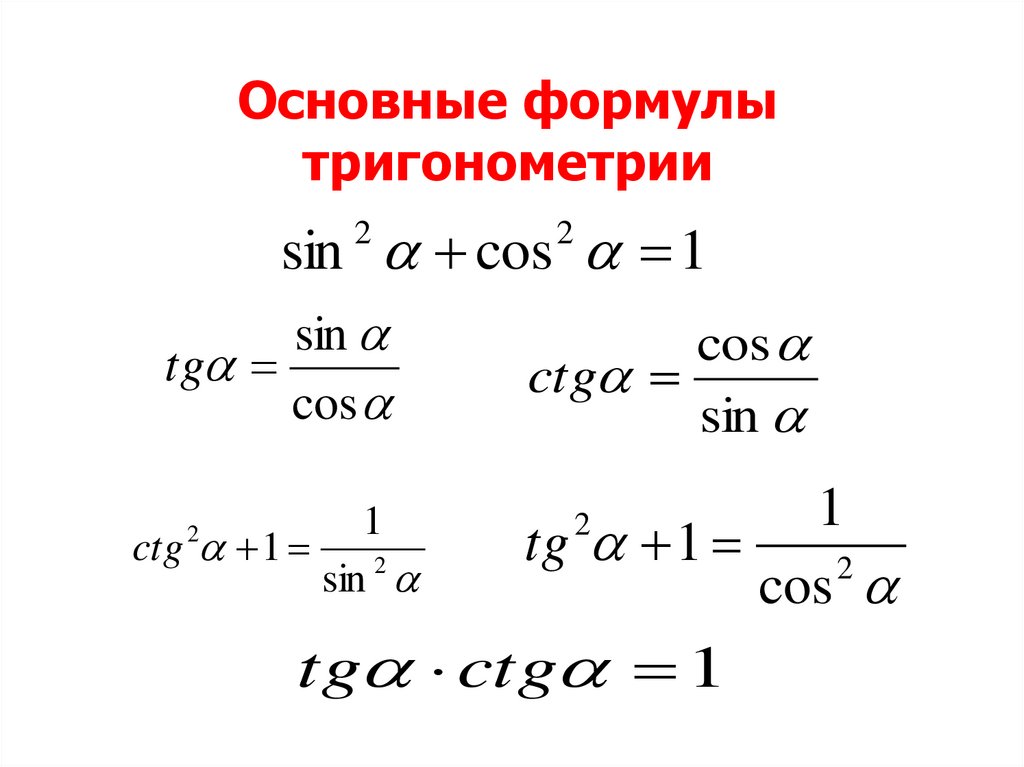
Основные формулытригонометрии
sin cos 1
2
sin
tg
cos
1
ctg 1
sin 2
2
2
cos
ctg
sin
1
tg 1
2
cos
2
tg ctg 1
6.
Формулы приведенияПравило для формул приведения:
1. Необходимо определить знак результата (по четверти).
2. Выяснить, меняется ли функция на кофункцию (если в
формуле присутствуют углы , 3 , то
2
2
происходит замена на кофункцию, т.е.: sin α cos α ;
cos α sin α
если в формуле углы
; tg α ctg α ; ctg α tg α;
,2
кофункцию не происходит).
,то замены на
7.
Формулы сложенияsin( ) sin cos sin cos
sin( ) sin cos sin cos
cos( ) cos cos sin sin
cos( ) cos cos sin sin
tg tg
tg ( )
1 tg tg
tg tg
tg ( )
1 tg tg
ctg ctg 1
ctg ( )
ctg ctg
8.
Формулы двойного аргументаsin 2 2 sin cos
2tg
tg 2
1 tg 2
cos 2 cos 2 sin 2
cos 2 1 2 sin 2
cos 2 2 cos 2 1
9.
Формулы тройного аргументаsin 3 3 sin 4 sin
3
cos 3 4 cos 3 cos
3
3tg tg
tg3
2
1 3tg
3
10.
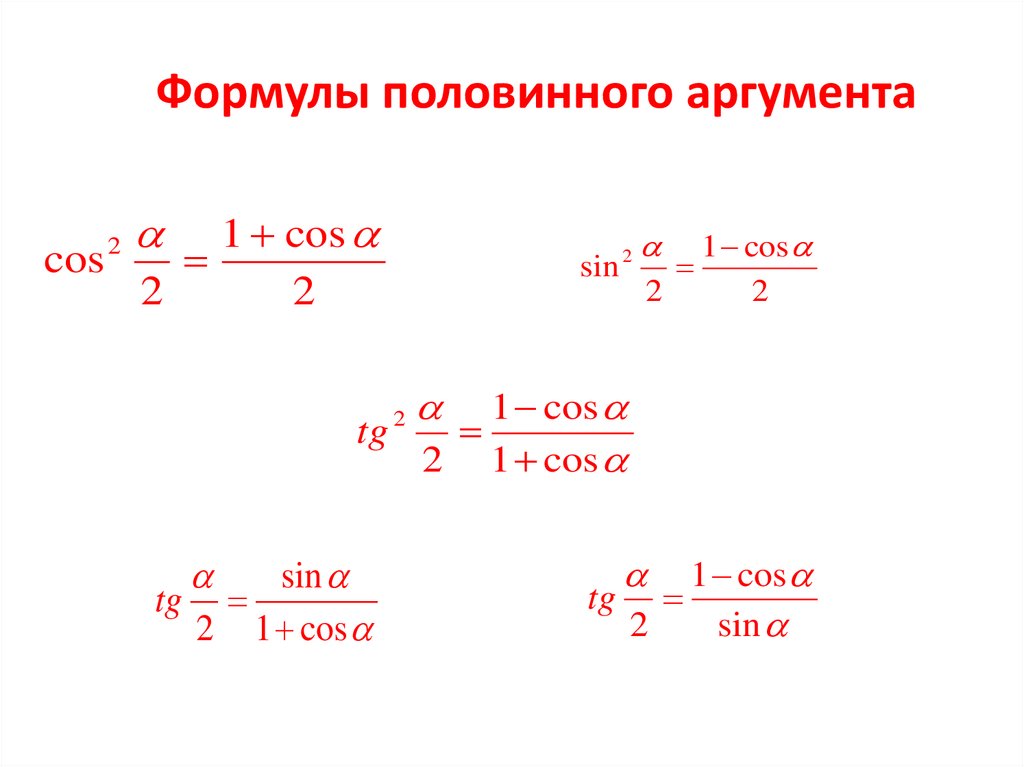
Формулы половинного аргумента1 cos
cos
2
2
2
sin 2
2
1 cos
2
1 cos
tg
2 1 cos
2
sin
tg
2 1 cos
1 cos
tg
2
sin
11.
Формулы суммы и разностисинусов, косинусов, тангенсов
sin sin 2 sin
cos
2
2
sin sin 2 sin
cos
2
2
cos cos 2 sin
sin
2
2
cos cos 2 cos
tg tg
sin( )
cos cos
2
sin( )
tg tg
cos cos
cos
2
12.
Арксинус, арккосинус, арктангенс,арккотангенс числа
13.
Тригонометрические уравненияТригонометрические уравнения - уравнения,
содержащие неизвестное под знаком тригонометрической
функции.
Решение тригонометрического уравнения
состоит из двух этапов:
• преобразование уравнения для получения его простейшего
вида
• решение полученного простейшего тригонометрического
уравнения.
14.
Решение простейшихтригонометрических уравнений
15.
Пример 1Решить уравнение:
2 sin 4 x 1 0
Уравнение переносом слагаемого и делением обеих частей легко
сводится к простейшему.
2 sin 4 x 1 0
4 x 1
2 sin 4 x 1
Разделим обе части на 4
t
k
x 1
k
1
sin 4 x
2
1
4 x 1 arcsin
k
2
k
16
4
k
k
4
x 1
k
Ответ:
16
k
4
16.
Пример 2Решить уравнение: cos 3 x 0
3
Уравнение уже имеет простейший вид t 3 x
3
Это частный вид уравнения cos t=a при a=0
3
3x
3x
2
2
3
k
k
3x
x
6
18
Ответ:
k
( 3)
k
3
k
x
18 3
17.
Пример 3Решить уравнение:
2 sin 2 x 5 sin x 2 0
Пусть sin x t , где t 1; 1 , тогда
2t 2 5t 2 0
t1 2, не удовлетворяет условию t 1; 1
t 2 1 ;
2
Вернемся к исходной переменной
1
sin x
2
1
n
x 1 arcsin πn , n Z
2
n π
x 1
πn , n Z
6
n π
Ответ : 1
πn , n Z .
6
18.
Пример 4Решить уравнение: 2cos2x-sinx+1=0
2(1-sin2x)-sinx+1=0
-2sin2x-sinx+3=0
2sin2x+sinx-3=0
Пусть sinx=y, -1≤y≤1
2y2+y-3=0
y1=-1,5- не подходит по условию
y2=1
Возвращаемся к старой переменной:
sinx=1
x
2
2 к , к Z
Ответ:
x
2
2 к , к Z
19.
Пример 5Решить уравнение:
3 cos 2x 5 cos x 1
3(2 cos 2 x 1) 5 cos x 1 0
6 cos 2 x 5 cos x 1 0
пусть cosx t
6t 2 5t 4 0
4
1
Корни этого уравнения t
и t
3
2
4
cos x
3
Решений нет
1
cos x
2
2
x 2 n, n Z
2
Ответ : x 2 n, n Z
3
3
20.
Пример 61
2
Решить уравнение: sinx - sin2x = 0
1
2
sinx – ∙2sinx · cosx = 0
sinx(1- cosx) = 0
1.
sinx=0
2.
1-cosx=0
cosx=1
x=∏k, k є Z
x=2∏n, nОтвет:
єZ
x к, к Z
21.
Пример 7Решить уравнение:
2 sin
cos 3x cos 5x sin 4x
3x 5 x
3x 5 x
sin
sin 4 x
2
2
2 sin 4 x sin( x) sin 4 x
2 sin 4x sin x sin 4x 0
Ответ:
sin 4 x( 2 sin x 1) 0
2 sin x 1
sin 4x 0
1
sin x
4x n
2
n
n
x ,n Z
x ( 1) n, n Z
4
6
22.
Пример 8Решить уравнение:
2 sin x cos x 0
2 sin x cos x 0
2 tg x 1 0
1
tg x
2
Ответ:
1
x arctg n, n Z
2
: cos x
23.
Пример 9Решить уравнение: 3 sin 2 x sin x cos x 4 cos 2 x 0
3 sin 2 x sin x cos x 4 cos 2 x 0
: cos2x
3tg 2 x tgx 4 0
пусть tg x t
3t 2 t 4 0
4
Корни этого уравнения t 1 и t
3
4
tg x 1
tg x
3
4
x arctg1 n
x arctg ( ) n
3
Ответ:
x
4
n, n Z
4
x arctg n, n Z
3
24.
Пример 10Решить уравнение: 3sin2x + 4sinx · cosx + 5cos2x = 2.
3sin2x + 4sinx · cosx + 5cos2x = 2sin2x + 2cos2x
sin2x + 4sinx · cosx + 3cos2x = 0 / : cos2x
tg2x + 4tgx + 3 = 0
Пусть tgx=y
отсюда y2 + 4y +3 = 0
корни этого уравнения:
y1 = -1, y2 = -3,
отсюда
1) tg x = –1,
x=-∏/4+∏k, k є Z
Ответ:
2) tg x = –3, x=-arctg3+∏n, n є Z
x=-∏/4+∏k, k є Z
x=-arctg3+∏n, n є Z




















 mathematics
mathematics








