Методика математического планирования эксперимента и анализа полученных результатов

1.

Методика математического
планирования эксперимента и
анализа полученных результатов

2.

В данной работе применялись план КОНО второго порядка для
двух факторов и план БОКСа второго порядка для трех факторов,
которые позволили значительно сократить время проведения работы
и повысить эффективность исследований.
Матрицы Д–оптимального плана обладают важными свойствами
в отношении коэффициентов регрессионной модели и выходного
параметра: ортогональностью, ротатабельностью и униформностью,
и обеспечивают получение минимума обобщенной дисперсии, то
есть минимума дисперсии всех коэффициентов регрессии (критерий S2{b} min).
Свойство ортогональности обеспечивает независимость полученных коэффициентов регрессии bi ,bij математической модели
второго порядка и возможность исключения членов модели с незначимыми коэффициентами без последующего пересчета значимых
коэффициентов.
Свойство ротатабельности обеспечивает постоянство дисперсии выходного параметра на равных расстояниях от центра эксперимента.
Свойство униформности обеспечивает постоянство дисперсии
выходного параметра в некоторой области эксперимента.

3.

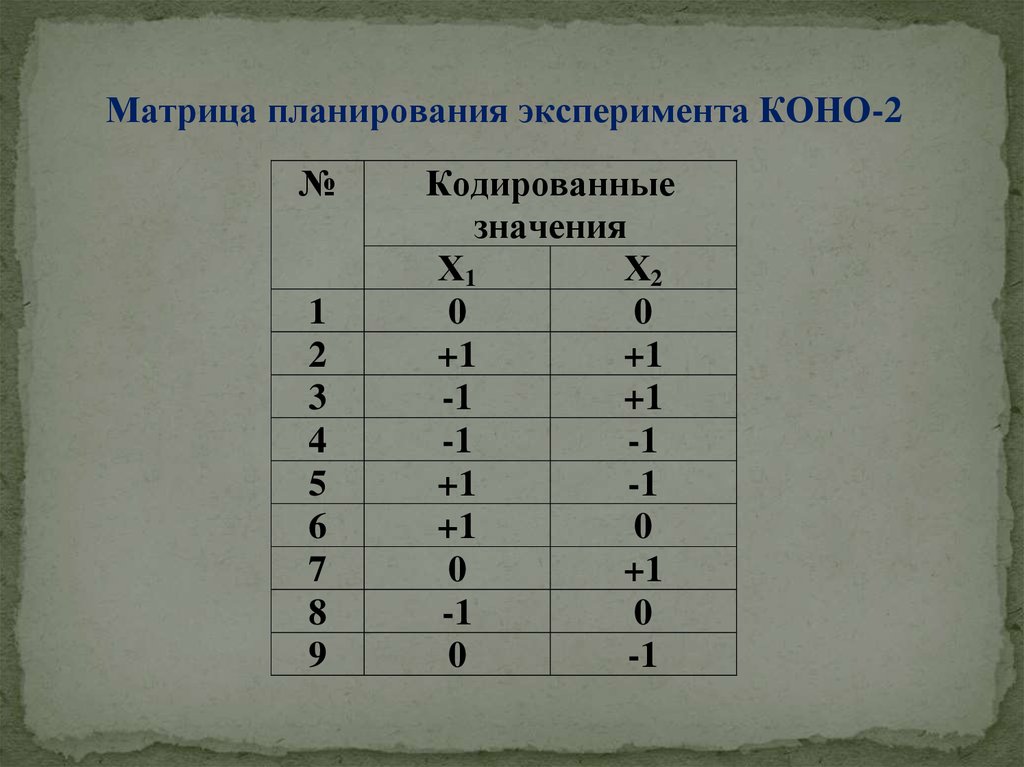
Матрица планирования эксперимента КОНО-2
№
1
2
3
4
5
6
7
8
9
Кодированные
значения
Х1
Х2
0
0
+1
+1
-1
+1
-1
-1
+1
-1
+1
0
0
+1
-1
0
0
-1

4.

Матрица планирования эксперимента БОКС-3
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Кодированные значения
Х1
Х2
Х3
+
+
+
+
+
+
+
+
+
+
+
+
+
0
0
0
0
0
+
0
0
0
0
0
+
0
0
-

5.

Полиномиальное уравнение имеет общий вид:
k
ck
Y = b0 +
bi xi +
bij xi xj + biin xi xj xn
i 1
ij 1
Mk
ijn 1
(1)
где
Y – расчетное значение критерия оптимизации,
k – число факторов оптимизации,
Ck – число сочетаний из двух факторов,
Mk – число сочетаний из трех факторов,
b0 – свободный член уравнения,
bi – линейные коэффициенты,
bij – коэффициенты, характеризующие двойное взаимодействие
факторов,
bijn – коэффициенты, характеризующие тройное взаимодействие
факторов,
xi, xj, xn – варьируемые факторы.

6.

Для перехода от матрицы планирования к рабочей матрице
используют соотношение, которое связывает кодированное
значение факторов с натуральными:
Х =
xi x0i
I
(2)
где Х – кодированное значение i-го фактора;
xi – текущее натуральное значение i-го фактора,
xoi – натуральное значение i-го фактора на нулевом уровне,
I – величина интервала варьирования i-го фактора в натуральных единицах.
Для случая, когда число факторов оптимизации равно двум,
то есть для плана КОНО-2, уравнение (1) принимает вид:
Y = b0 +b1 x1 +b2 x2 +b12 x1 x2 +b11 x12 +b22 x22
(3)
Для случая, когда число факторов оптимизации равно трем,
уравнение (1) принимает вид:
Y =b0+b1 x1+b2 x2+b3 x3+b12 x1 x2+b13 x1 x3+b23 x2 x3+b11 x12+b22
x22+b33x32 (4)

7.

Определение
коэффициентов
регрессии
проводится
следующей последовательности:
1) Нахождение среднего значения функции отклика
по строкам:
Yu =
в
m
Yi
1
m
i 1
(5)
2) Определение построчных дисперсий:
Su2 {Y} =
m
(Yi – Yu)2
1
k ( N Nц 1)
i 1
(6)
3) Проверка однородности дисперсий по критерию Кочрена,
расчетное значение которого:
N
GR = Su max2 {Y}/
u 1
Su2 {Y}
(7)
Полученное значение сравнивается с табличным.
Если GR ‹ GT , то гипотеза об однородности дисперсий
не отвергается.
4) Оценка дисперсии воспроизводимости:
1
S {Y} = k ( N Nц 1)
2
N
m
1
1
(Yi – Yu)2 ,
где N – число опытов в матрице.
(8)

8.

5) Вычисление коэффициентов уравнения:
N
b0 = g1 Yu – g2
i 1
m
N
i 1
u 1
xiu2 Yu
(9)
N
bi = g3
u 1
xiu Yu
(10)
xiu xju Yu
(11)
N
bij = g4
u 1
N
bii = g5
u 1
m
xiu2
Yu + g6
N
i 1
u 1
N
xiu2
Yu – g2
Yu
u 1
(12)
где
Yu – среднее экспериментальное значение критерия оптимизации,
g1 – g6 – постоянные коэффициенты.

9.

6) Определение дисперсий коэффициентов регрессии:
S2{b0} = g1 S2{Y}
(13)
S2{bi} = g3 S2{Y}
(14)
S2{bij} = g4 S2{Y}
(15)
S2{bii} = g7S2{Y}
(16)
Их ковариации:
cov{b0} = g2 S{Y}
(17)
cov{bii bij} = g6 S{Y}
(18)
7) Расчет дисперсии адекватности:
N
Sад2{Y} =
n(Yu – Yu)2 / (N – Л)
u 1
(19)
где Yu – расчетное значение критерия оптимизации,
Л – число коэффициентов регрессии:
Л = (k+2)(k+1)/2 ,
(20)
где k – число варьируемых факторов.
Например, для эксперимента, проводимого по матрице
БОКС-3, Л=10.

10.

8) Определение значимости коэффициентов регрессии с помощью критерия Стьюдента:
tR{bi} = |bi| / S{bi} > tт
,
(21)
где tт – табличное значение критерия Стьюдента.
9) Для проверки адекватности полученной регрессионной модели второго порядка используют критерий
Фишера:
FR = Sад2{Y} / S2{Y}
(22)
Если FR < Fт , то модель считается адекватной с выбранной доверительной вероятностью.
Полученные в результате расчетов конкретные
уравнения регрессии оценивались аналитически и
графически в виде поверхностей отклика.