Оптимальное планирование эксперимента

1. Оптимальное планирование эксперимента

2. Литература

1.
2.
3.
Н.А. Спирин, В.В. Лавров. Методы
планирования и обработки инженерного
эксперимента: Конспект лекций. Под общ.
Ред. Н.А. Спирина. Екатеринбург: ГОУ ВПО
УГТУ-УПИ, 2004.-257с
Джонсон Н. Лион Ф. Статистика и
планирование эксперимента в технике и
науке: Методы планирования эксперимента. –
М.: Мир, 1981. – 520 с.
Красовский Г.И., Филаретов Г.Ф.
Планирование эксперимента. – Мн.: Изд-во
БГУ, 1982. – 302 с.

3. Цель планирования эксперимента

нахождение таких условий и
правил проведения опытов при
которых удается получить
надежную и достоверную
информацию об объекте с
наименьшей затратой труда, а
также представить эту
информацию в компактной и
удобной форме с количественной
оценкой точности

4. Вводные понятия

Эксперимент – система операций, воздействий и
(или) наблюдений, направленных на получений
информации об исследуемом объекте [1]
Опыт – воспроизведение исследуемого явления в
определенных условиях проведения эксперимента
при возможности регистрации его результатов [1]
Фактор – переменная величина, по предположению
зависящая влияющая на результат эксперимента
Отклик – наблюдаемая случайная переменная, по
предположению зависящая от факторов [1]
Функция отклика – зависимость мат. ожидания
отклика от факторов [1]

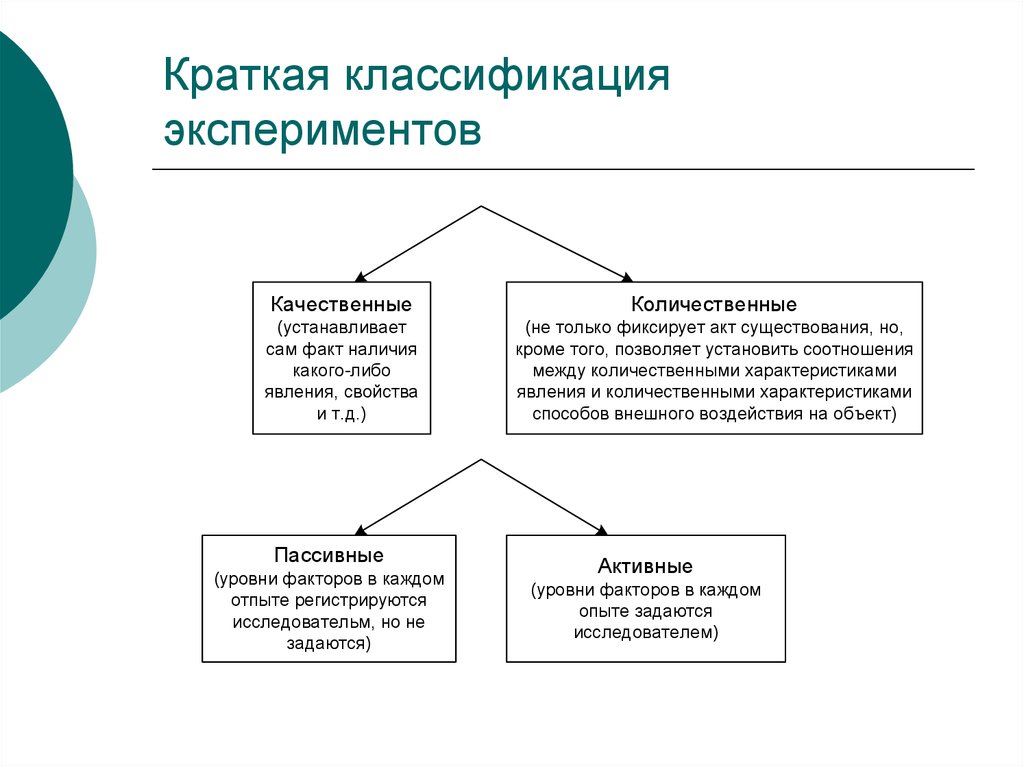
5. Краткая классификация экспериментов

Качественные
Количественные
(устанавливает
сам факт наличия
какого-либо
явления, свойства
и т.д.)
(не только фиксирует акт существования, но,
кроме того, позволяет установить соотношения
между количественными характеристиками
явления и количественными характеристиками
способов внешного воздействия на объект)
Пассивные
(уровни факторов в каждом
отпыте регистрируются
исследовательм, но не
задаются)
Активные
(уровни факторов в каждом
опыте задаются
исследователем)

6. Функция отклика

- это зависимость математического ожидания отклика от
факторов [1]
M y f ( xi , h j )
M y математическое ожидание отклика
xi контролируемые и управляемые факторы
hi контролируемые, но неуправляемые факторы
ошибка эксперимента

7. Активный эксперимент

Полнофакторный эксперимент (ПФЭ) – эксперимент, реализующий все
возможные неповторяющиеся комбинации уровней независимых факторов
Основная задача – определить коэффициенты
k
k
k
i 1
i ,u 1
i 1
функции отклика
(*) y 0 i xi i ,u xi xu ii xi ...,
2
Уравнение (*), используется для описания функции отклика в связи с ее
априорной неизвестностью
x, x – переменные факторы при i=1,…k; u=1,…k; i!=u (k-число факторов)
f
i
xi
2 f
; iu
o
xi xu
2 f
; ii
2 x 2
o
i o
k
k
k
2
y b0 bi xi bi ,u xi xu bii xi ...,
i 1
i ,u 1
i 1
коэффициенты влияния
факторов
регрессионная модель
(коэффициенты регрессии
определяются экспериментально)
b 0 , bi i , biu iu , bii ii

8. Последовательность проведения активного эксперимента

1.
2.
3.
Разрабатывается схема проведения
исследований, т.е. выполняется
планирование эксперимента
Осуществляется реализация опыта по
заранее составленному
исследователем плану, т.е.
осуществляется сам активный
эксперимент
Выполняется обработка результатов
измерений

9. Планирование активного эксперимента

При планировании экспериментов чаще всего применяются планы
1-ого и 2-ого порядков. Планы более высоких порядков
применяются редко из-за их большой вычислительной сложности
Планы 1-ого порядка – это планы, которые позволяют провести
эксперимент для отыскания уравнения регрессии, содержащее
только первые степени факторов и их произведения
k
y b0 bi xi
i 1
k
b
i ,u 1
i i
iu
xi xu
k
b
i , j 1
i j u
x x j xu ...
iju i
Планы 2-ого порядка – это планы, которые позволяют провести
эксперимент для отыскания уравнения регрессии, содержащие вторые
степени факторов
k
k
2
y b0 bi xi bii xi
i 1
i 1
k
b
i ,u 1
i u
iu
xi xu ...

10. Планирование первого порядка

В качестве факторов выбираются
только контролируемые и управляемые
факторы (переменные)
Обеспечивается возможность
независимого изменения каждого из
факторов и поддержание его на
определенном уровне
Для каждого фактора указывается
интервал (+/-), в пределах которого
ставится исследование

11. Представления плана эксперимента (на примере эксперимента с 3-мя независимыми факторами)

b0, b1, b2, b3 – коэффициенты
регрессии
xi*xu – члены двойного
взаимодействия
Уравнением регрессии
3
3
y b0 bi xi bui xi xu b123 x1 x 2 x3
i 1
i ,u 1
i u
x1*x2*x3 – члены тройного
взаимодействия
Геометрическое представление
Табличное (матричное) представление
План
Номер
опыта
x0
x1
x2
x3
x1x2
x1x3
x2x3
x1x2x3
Результат
y
1
+1
-1
-1
-1
+1
+1
+1
-1
y1
2
+1
+1
-1
-1
-1
-1
+1
+1
y2
3
+1
-1
+1
-1
-1
+1
-1
+1
y3
4
+1
+1
+1
-1
+1
-1
-1
-1
y4
5
+1
-1
-1
+1
+1
+1
-1
+1
y5
6
+1
+1
-1
+1
-1
-1
-1
-1
y6
7
+1
-1
+1
+1
-1
+1
+1
-1
y7
8
+1
+1
+1
+1
+1
-1
+1
+1
y8

12. Свойства матрицы представления эксперимента

1. Свойство симметричности – алгебраическая сумма элементов векторстолбца каждого фактора равна нулю (за исключением столбца,
соответствующего свободному члену)
n
X
j 1
0,
ij
i = номер фактора, j – номер опыта
2. Свойство нормирования – сумма квадратов каждого столбца равна
числу опытов
n
X
j 1
2
ij
n;
3. Свойство ортогональности – скалярное произведение всех векторстолбцов (сумма почленных произведений элементов любых вектор
столбцов) равно нулю
n
X
j 1
ij
X uj 0, i u

13. Определение коэффициентов b уравнения регрессии

Методом наименьших квадратов находятся
оценки b коэффициентов
По свойствам матрицы планирования
- (ссимметри ность) b0 X 1 j 0;
y b0 b1 x1 b2 x2
(нормирования) b1 X 1 j nb1 ;
2
2
y j y j min
n
(ортогональность) b2 X 1 j X 2 j 0;
bi
j 1
n
2 y j b0 b1 X 1 j b2 X 2 j X 1 j 0;
b1
j 1
n
y
j 1
1j
n
n
j 1
j 1
n
X 1 j b0 X 1 j b1 X 1 j b2 X 1 j X 2 j 0;
2
j 1
Получаем
n
b1
y X
j 1
j
n
1j
; b2
n
y X
j 1
j
n
n
b12
y j X 1 X 2 j
j 1
n
n
2j
; b0
y X
j 1
; b123
y X
j 1
0j
n
n
j
j
1
n
X 2 X3 j

14. Планирование второго порядка

Применяется если
описание функции
отклика первым порядком
получается
недостаточным
(например, процесс носит
нелинейный характер)
Каждый фактор
варьируется не менее чем
на трех уровнях – полный
эксперимент содержит
3^k (k – количество
факторов) опытов.
Опыты проводятся
1. В «крайних точках» - как в
планировании 1-ого порядка
2. В «звездных точках» - xi=(+/-)a,
xj=0, 1,…,n; 1,…,n; i!=j
3. В «центре» - xi=0, j=1,2,3,…,n
План 2-ого порядка при k=2 n=1
2
2
y b0 b1 x1 b2 x2 b11 x1 b22 x2 b12 x1 x2
Уравнение регрессии для
эксперимента с 2-мя факторами

15. Ортогональный план

Это план 2-ого
порядка после
преобразован
ий (*)
Эти
преобразован
ия позволяют
усреднить
случайные
погрешности
Ортогональный план 2-ого порядка
n
(*) xij xij
2
x
j 1
2
ij
xij xi
2
n
2
Тогда уравнение регрессии
y b0 bi xi biu xi xu bii xi ;
k
k
k
j 1
i ,u 1
i 1
В итоге уравнение регрессии преобразуется к виду
k
y b0 bi xi
j 1
k
b
i ,u 1
iu
2
2
xi xu bii ( xi xi )
k
i 1

16. Ротатабельный план

Это план, у
которого точки
плана
располагаются
на окружностях
(сферах,
гиперсферах)
Ротабельный план 2-ого порядка
В таком плане точность оценивания
функции отклика по любому направлению
факторного пространства (для всех точек
плана) одинаковая, что позволяет
наилучшим образом извлечь максимальное
количество (несмещенной) информации из
плана
Для того, что бы привести план 2-ого
порядка к рототабельному величину плеча
выбирают из условия (**)
k
4
(**) 2 при k 5 и 2
k 1
4
при k 5