Similar presentations:
Планирование эксперимента
1.
Лекция 4. Основы планирования эксперимента.Дополнительная литература по теме:
1. Фишер Р.А. Планирование эксперимента. Монография.
2. Налимов В.В. Теория эксперимента. М.: Наука, 1971. 207 c.
3. Монтгомери Д.К. Планирование эксперимента и анализ данных: перевод с английского.
М.: Мир, 1981. 520 c.
2.
Виды экспериментаВид эксперимента
Особенности/цель
1. Элиминирующий
Выявить и устранить влияние неоднородностей
2. Сравнительный
Оценить влияние каждого фактора на процесс
3. Отсеивающий
Отобрать для исследования существенные
факторы
4. Экстремальный
Выбор оптимальных режимов проведения
эксперимента
5. Аппроксимирующий
Выявление математической модели процесса
6. Численный
Замена физического эксперимента
математической моделью
7. Идентифицирующий
Определение характеристик/коэффициентов
в математической модели объекта
8. Экстраполирующий
Предсказание изменений параметров объекта
1
3.
Задачи c использованием планирования эксперимента- Поиск оптимальных условий проведения эксперимента;
- построение интерполяционных формул;
- выбор существенных факторов;
- оценка и уточнение констант теоретических моделей...
Схема «черного ящика»
Z1, Z2, …, Zi
(неуправляемые факторы)
X1, X2, …, Xi
(факторы)
Объект
испытания
Y1, Y2, …, Yi
(параметры
оптимизации)
v1, v2, …, vi
(неконтролируемые факторы)
2
4.
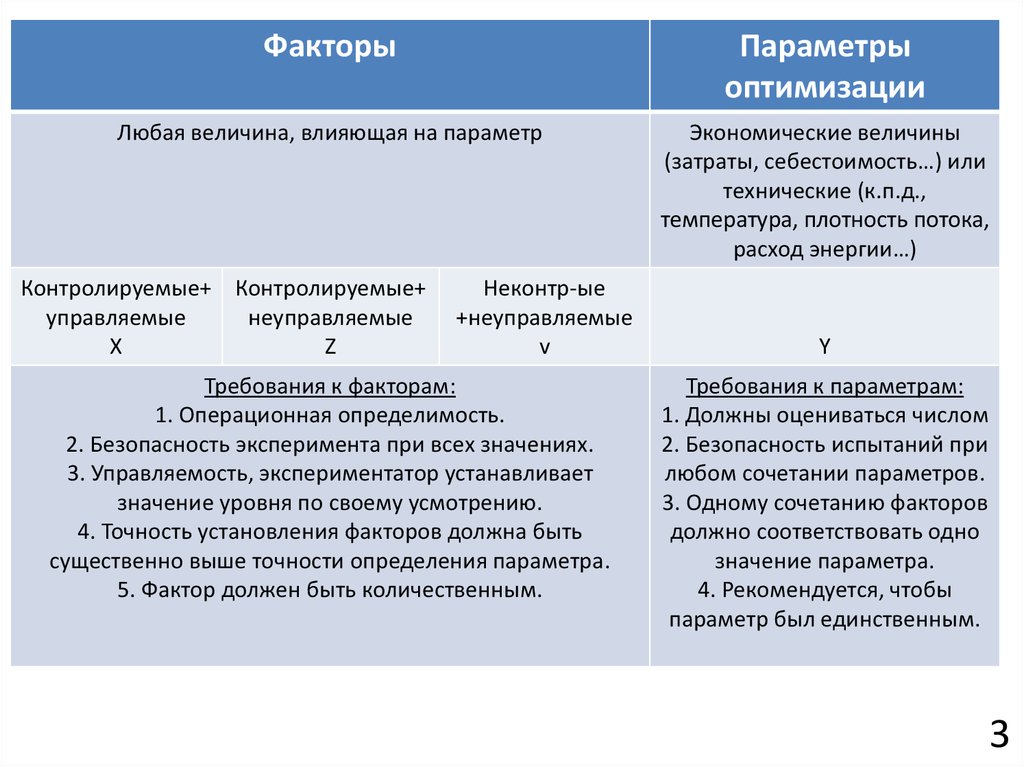
ФакторыПараметры
оптимизации
Любая величина, влияющая на параметр
Экономические величины
(затраты, себестоимость…) или
технические (к.п.д.,
температура, плотность потока,
расход энергии…)
Контролируемые+ Контролируемые+
управляемые
неуправляемые
X
Z
Неконтр-ые
+неуправляемые
v
Требования к факторам:
1. Операционная определимость.
2. Безопасность эксперимента при всех значениях.
3. Управляемость, экспериментатор устанавливает
значение уровня по своему усмотрению.
4. Точность установления факторов должна быть
существенно выше точности определения параметра.
5. Фактор должен быть количественным.
Y
Требования к параметрам:
1. Должны оцениваться числом
2. Безопасность испытаний при
любом сочетании параметров.
3. Одному сочетанию факторов
должно соответствовать одно
значение параметра.
4. Рекомендуется, чтобы
параметр был единственным.
3
5.
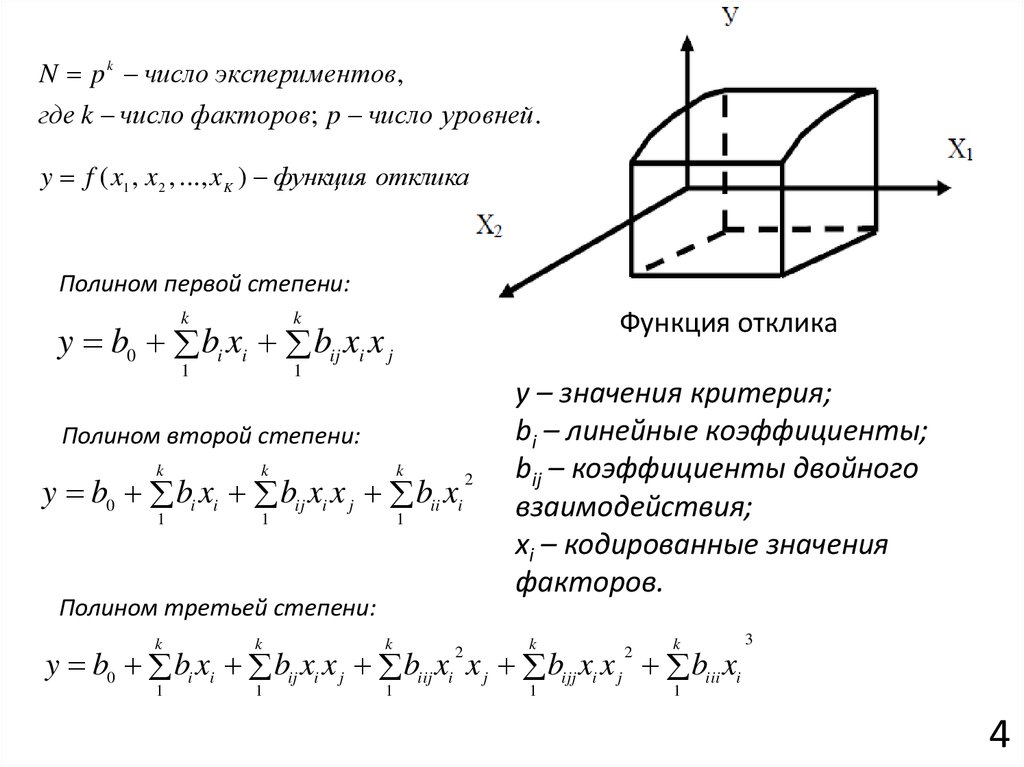
N p k число экспериментов,где k число факторов; p число уровней.
y f ( x1 , x2 , ..., x K ) функция отклика
Полином первой степени:
k
k
1
1
Функция отклика
y b0 bi xi bij xi x j
Полином второй степени:
k
k
k
1
1
1
y b0 bi xi bij xi x j bii xi
Полином третьей степени:
k
k
k
1
1
1
2
y – значения критерия;
bi – линейные коэффициенты;
bij – коэффициенты двойного
взаимодействия;
xi – кодированные значения
факторов.
k
k
y b0 bi xi bij xi x j biij xi x j bijj xi x j biii xi
2
1
2
3
1
4
6.
Относительные единицы факторовПример:
T, оС
30
40
50
x
-1
0
+1
xi xi 0
xi
xi
где ∆xi – разница между средним и минимальным значением
фактора (интервал варьирования);
xi – значение фактора в абсолютных величинах;
xi0 – абсолютное значение фактора в центре эксперимента;
Если, например, xi =45, то его значение в относительных единицах:
45 40
xi
0,5
10
5
7.
Обобщенный параметр оптимизации YЕсли один параметр обозначить через y1, а другой – через y2, и число опытов N,
N y
N y
то коэффициент парной корреляции r будет:
1u
2u
y1
N
( y1u y1 ) ( y2 u y2 )
ry1 y 2
u 1
u 1
N
N
( y1u y1 ) ( y2 u y2 )
2
u 1
N
; y2
u 1
N
.
1) Минимальность отклонений откликов от опт.
2
2
2
y y1ОПТ
y y2ОПТ
k 2 2
...
y k1 1
y1Э
y2 Э
u 1
2) Построение отклика по двухбалльной шкале.
1, если y1i 30
1, если y2 i 85
n
y1i
;
y2i
;
0
,
если
y
30
0
,
если
y
85
Yi yui
1i
1i
u 1
1, если y3i 110
1, если y 4 i 2500
y 3i
;
y4i
.
0, если y3i 110
0, если y4 i 2500
Обоб
№
Отклики
Преобразованные отклики
щенный
опыта
параметр
y1
y2
y3
y4
y1
y2
y3
y4
Y
1
25
83
115
2900
1
0
0
0
0
2
27
86
105
2450
1
1
1
1
1
3
31
89
102
2490
0
1
1
1
0
4
29
88
109
2400
1
1
1
1
1
5
33
86
117
2590
0
1
0
0
0
6
8.
2) Функция желательности Харрингтона.Предпочтительность du
Отметки
Отлично
1,00 – 0,80
Хорошо
0,80 – 0,63
Удовлетворительно
0,63 – 0,37
Плохо
0,37 – 0,20
Очень плохо
0,20 – 0,00
d ( yбезр ) e
e y
n
Yi
d j
j 1
n
7
9.
Предварительное изучение объекта1) Сбор априорной информации.
2) Формулирование цели работы.
3) Составление схемы эксперимента: список и
классификация факторов.
4) Выбор критерия.
5) Проведение отсеивающего эксперимента (метод
ранговой корреляции, метод случайного баланса, метод
насыщенного планирования).
6) Выбор основного уровня – наилучшая комбинация
факторов на основе предварительного изучения объекта.
7) Определение интервалов варьирования факторов.
8
10.
Полный факторный экспериментМатрица планирования эксперимента 22
N p k 2 2 4.
y b0 b1 x1 b2 x2
№ опыта
x1
x2
y
1
+1
+1
y1
2
-1
+1
y2
3
+1
-1
y3
4
-1
-1
y4
N
N
b0
yi
i 1
N
b0
bj
x ji yi
i 1
N
, j 0, 1, ...k
y1 y2 y3 y4
4
b1
( 1) y1 ( 1) y2 ( 1) y3 ( 1) y4
4
b2
( 1) y1 ( 1) y2 ( 1) y3 ( 1) y4
4
9
11.
Матрица планирования эксперимента 23№ опыта
x1
x2
x3
y
1
+
+
+
y1
2
-
+
+
y2
3
+
-
+
y3
4
-
-
+
y4
5
+
+
-
y5
6
-
+
-
y6
7
+
-
-
y7
8
-
-
-
y8
Первое свойство
N
x ji 0, j, i номера фактора и опыта соответств енно.
i 1
Второе свойство
N
x
i 1
2
ji
N
Третье свойство
N
x ji xui 0, j, u номера двух любых вектор столбцов.
i 1
10
12.
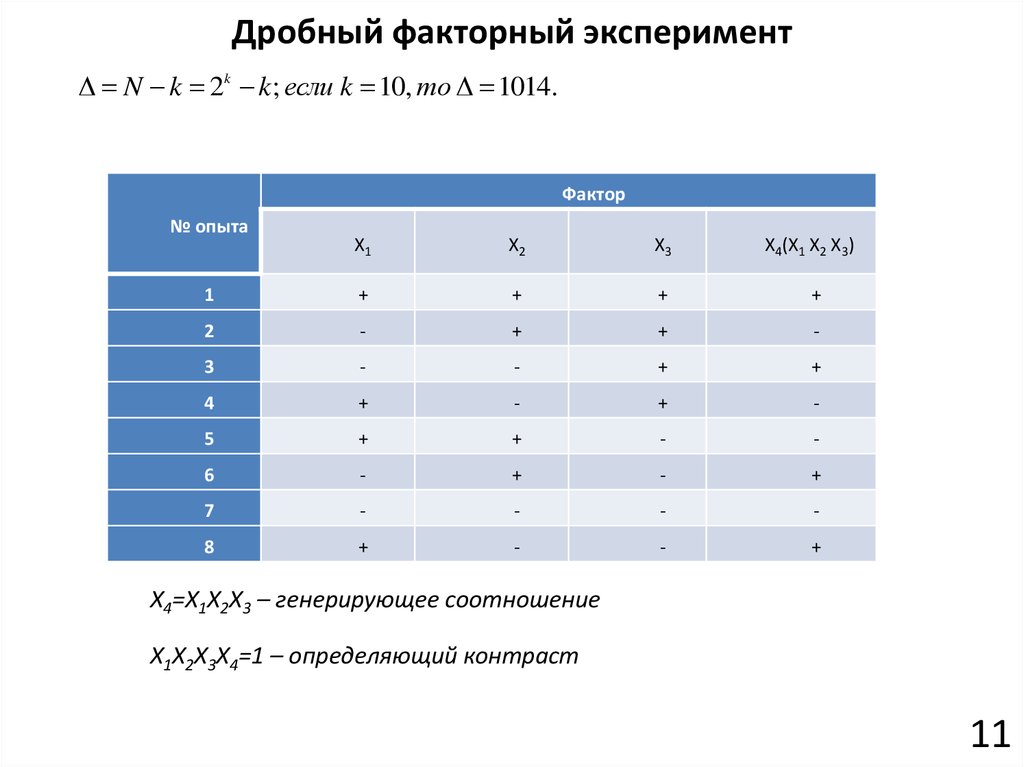
Дробный факторный экспериментN k 2k k; если k 10, то 1014.
Фактор
№ опыта
X1
X2
X3
X4(X1 X2 X3)
1
+
+
+
+
2
-
+
+
-
3
-
-
+
+
4
+
-
+
-
5
+
+
-
-
6
-
+
-
+
7
-
-
-
-
8
+
-
-
+
X4=X1X2X3 – генерирующее соотношение
X1X2X3X4=1 – определяющий контраст
11
13.
Планирование эксперимента в современных пакетах(Ansys DesignXplorer)
- Поиск условий для достижения наилучших характеристик;
- определение ключевых параметров, влияющих на конструкцию;
- исследование робастности конструкции.
Одиночный расчет
Ручной перебор вариантов
Поверхность отклика
1) Корреляционный анализ – поиск отношений между параметрами.
2) Планирование эксперимента (расчет необходимого набора вариантов)
3) Поверхность отклика – построение математической модели
4) Оптимизация (на основе поверхности отклика или прямые методы)
5) Анализ робастности, расчет 6-сигма.
12
14.
1.2.
3.
4.
5.
6.
Центральный композиционный план (CCD) (по умолчанию)
План Бокса-Бенкена
План оптимального заполнения пространства
Настраиваемый + заполнение
Инициализация разреженной сетки
Заполнение по методу Латинского Гиперкуба
13











 mathematics
mathematics








