Обработка результатов эксперимента. Матричное исчисление

1. Обработка результатов эксперимента

Матричное исчисление

2. Регрессионный анализ

• Это статистический метод проверки гипотезы о пригодности
модели и значимости коэффициентов. Он основывается на
следующих постулатах:
• Параметр у – есть случайная величина.
• Дисперсия у – не зависит от абсолютной величины у.
• Значения факторов – есть не случайные величины.
• Наиболее простым классом регрессионной модели является
У
У
• y=b0+b1x1+b2x2+….+
• Вектор параметров такой
модели находят при
условии минимизации
ее ошибки, т.е. МНК
Х
Х
N
2
S ад
.
y
i 1
f
2

3. Матричные исчисления в многомерной статистике

• Для нахождения коэффициента регрессии в матричном исчислении необходимо решить следующие уравнения:
• , где X– матрица условий эксперимента. Y – матрица
результатов эксперимента, В - матрица столбец коэффициентов уравнения
x 0…N условный фактор для оценки b0 , т.к. для остальных b1 ,b2
и т.д. есть значения
x01
x
02
x
0N
x11
x12
x1N
xK1
xK 2
x KN
x1 ...xK
b0
b
1
b
2
b
K
.
y1
y
2
y
N
XT
x 01
x
11
x
K1
x 02
x12
xK 2
x0 N
x1N
x KN

4. Решим матрицу относительно В

• Умножив обе части равенства на транспонированную матрицу:
X T X X T
• Получим информационную матрицу Фишера
N
N
N
2
• Ее структура
x0 n
( xon x1n ) ( xon xkn )
1
N
( xon x1n )
A
1
N
(x x )
kn on
1
A XT X
1 x12n 1 ( x1n xkn )
N
N
2
1 ( xkn x1n ) 1 x kn
1
N
1
N
• приведенная информационная матрица
M
1
A
N

5.

• Чтобы найти коэффициент уравнения, необходимо, чтобы в
левой части получилась единичная матрица, тогда правая часть
будет решением данного уравнения. Найдем матрицу обратную
А и умножим на нее слева обе части уравнения.
X
T
X
X
1
T
X X X
T
1
E X X
• Отбросив единичную матрицу.
A 1
X
T
X
XT
T
XT X
• определитель матрицы
• присоединенная матрица
XT X
• Структура матрицы Фишера
xon y
x1n y
T
x y
kn
X
T
X
C 00
C
A 1 10
C
K0
C 01
C11
C K1
C0 K
C1K
C KK
1
XT

6.

b0 C 00
b1 C10
b C
k k0
C 01 C 0 k x0 n y
C11 C1k x1n y
C k1 C kk x kn y
N
• Каждый bi определяется по следующей формуле
N
bi Ci xin y n
• При ортогональном планировании:
i 1
n 1
C 00
0
0
N
xiu y ju 0
u 1
i j
N
bi Cii x1u yu
x
in
N
u 1
yn
0
C11
0
0
0
1
A
C kk
Cii
1
xiu2
N xiu2 посвойствуПФЭ
• Аналогичны рассуждения при проверке дисперсии экспериментов
C 00
1
C
X T X S y2 10
C
k0
C 01
C11
C k1
C0k
S 2 b0
C1k 2 cov b0 b1
Sy
cov b b
C kk
0 k
cov b0 b1
S 2 b1
cov b1bk
cov b0 bk
cov b1bk
2
S bk

7. Ковариация

Если ковариация положительна, то с ростом значений одной случайной
величины, значения второй имеют тенденцию возрастать, а если знак
отрицательный — то убывать.
Однако по абсолютному значению ковариации нельзя судить о том,
насколько сильно величины взаимосвязаны, так как её масштаб
зависит от их дисперсий. Масштаб можно нормировать, поделив
значение ковариации на произведение среднеквадратических
отклонений, т.е.это коэффициент корреляции, который всегда
находится в интервале от −1 до 1.

8. Критерии оптимальности планов

КРИТЕРИИ
ОПТИМАЛЬНОСТИ ПЛАНОВ

9. Требования к матрице ковариаций

• Построение плана эксперимента можно интерпретировать
как
выбор
строк
матрицы
х,
их
числа
и
последовательности
проведения.
Этот
выбор
осуществляется разными способами, а => коэффициенты
b могут быть оценены с разной точностью, будут иметь
разные
ковариации
(критерий
оптимальности).
Требования к модели удобно формировать в терминах
свойств матрицы .
• Первая группа коэффициентов – критерии, связанные с
точностью
оценок
коэффициентов
регрессии.
(Интерпретация может быть алгебраической (а),
геометрической (б) и статистической (в).)
• Критерии, определяющие точность предсказаний
значений отклика с помощью построенных моделей.

10. Первая группа

N
x ji xui 0
j u
1.1. Ортогональность.
i 1
а). диагональность матрицы дисперсии – ковариации.
б). направление главных осей эллипсоида рассеяния совпадает с
направлением координатных осей пространства.
в). оценки параметров коэффициентов независимы друг от друга.
cov bu b j 0
j u
1.2. D – оптимальные планы.
а). минимум определителя матрицы дисперсии – ковариации.
б). минимум объема эллипсоида рассеяния параметров.
в). минимум обобщенной дисперсии всех коэффициентов.
1.3. А – оптимальность.
а). минимум следа матрицы дисперсии, ковариации.
б). минимум суммы квадратов длин осей эллипсоида рассеяния и
минимум длины диагонали прямоугольника, описанного около
эллипсоида.
в). минимальная средняя дисперсия оценок эксперимента.

11.

1.4. Е – оптимальные планы (minmax).
а). minmax собственного значения матриц дисперсии,
ковариации.
б). min максимальной оси эллипсоида рассеяния.
в). отдельные оценки параметров не обладают слишком
большими дисперсией и ковариацией.
1.5. minmax оценки дисперсии коэффициентов.
а).
minmax диагонали элемента матрицы.
б). минимум максимальной проекции оси эллипсоида
рассеяния на координатные оси пространства параметров.
в). minmax дисперсии оценки коэффициентов.

12. Вторая группа

2.1. ротатабельность.
а).
, где - сферическая координата.
в). одинаковая точность предсказаний для точек, равноудаленных
от центра плана по любому направлению.
2.2. униформность.
T
1
а). при X i M X i const при 0 1
в). дисперсия предсказания постоянна в некоторой области
вокруг центра эксперимента (интервал варьирования может
увеличиваться и уменьшаться без болезненно).
2.3. G – оптимальность.
а)
в) Minmax – максимального значения дисперсии оценки
поверхности отклика.
2.4.Q – оптимальность. а)
б) Минимум средних дисперсий оценки поверхности отклика.
Критерии насыщенности плана и критерии композиционности
плана.

13. Критерии насыщенности и композиционности плана.

• Насыщенность плана обеспечивает минимум числа
опытов. Минимум задается числом коэффициентов
модели. Приближение к нему служит мерой
насыщенности плана.
• В общем случае Кнас N (k+1), где k- число констант
модели.
• Процессы, протекающие в многофазных системах, как
правило, не удается описать линейными регрессионными
закономерностями. Поэтому необходимо использовать
математические модели более высокого порядка. Это и
есть ортогональное композиционное планирование
эксперимента.

14. Планы второго порядка

ПЛАНЫ ВТОРОГО ПОРЯДКА

15. Особенности планов второго порядка

• При наличии в исследуемой области не более одного
экстремума в качестве модели системы используют
n
n
n
зависимость следующего вида:
0 i xi ij xi x j i xi2
• -истинная величина отклика.
1 i k
1 i j k
1 i k
• -истинное значение коэффициента.
k 1 k 2
• Особенность данного метода: число опытов для N
2
построения такой модели должно быть не меньше:
• Если k число варьирования факторов.
• Для данного вида эксперимента каждый фактор должен
варьироваться, по крайней мере на трех уровнях. Для
построения модели существует огромное число планов,
приведенных в справочниках.

16. Планы типа 3n

Планы типа
n
3
Планы с числом степеней свободы, достаточным для получения
оценок всех коэффициентов данной модели, можно было бы
построить, например, введением трех уровней варьирования для
каждой из переменных исследуемой системы. Но такие планы
обладали бы большой избыточностью степеней свободы, т. е.
12
избыточностью числа xопытов.
• n = 2, коэффициентов – 6, опытов – 9.
• Для n = 3, 27 опытов, 10 коэффициентов.
• Поэтому такие планы полностью никогда не реализуют. Действительно
реализуемыми остаются например:
• Это матрица плана второго порядка,
построенного для n=3 на базе
x3
x3
x1
x1
x1
x2
x2
x2
3
матрицы ПФЭ З . Как видно, из 27
+
+
0
+
0
–
0
–
+
–
0
–
0
+
0
–
опытов в матрице плана осталось
–
+
0
–
0
–
0
0
всего 12 и добавлены три опыта в
–
–
0
0
+
+
0
0
центре, т. е. предусматривается
+
0
+
0
+
–
0
0
всего 15 опытов
3
x3
+
–
0
0
0

17. Коэффициенты модели

n0
n
b0
you
u 1
N
bi A ~
xiu y u
u 1
no
N
bij D ~
xiu ~
x jn y u
u 1
N
n
N
bii B x y u C x y u
u 1
2
1u
i 1 u 1
2
in
y
u 1
ou
n0 P
где A, B, C, D – некоторые коэффициенты, взятые из таблицы.
Ошибки оценок коэффициентов
модели могут быть вычислены
через соответствующие
дисперсии
Геометрический смысл плана
Данной моделью целесообразно пользоваться
только, если используется сразу полином
второй степени. Эту модель не рационально
использовать, если до этого проводился ПФЭ.

18. Центральные композиционные планы

Планы второго порядка, построенные на базе линейных факторных
планов типа 2n добавлением к ним некоторого числа определенным
образом расположенных экспериментальных точек (центральные
композиционные планы второго порядка), получили в настоящее время
наиболее широкое использование.
Дополнительными точками в центральных композиционных планах
второго порядка являются так называемые “звездные” точки, задаваемые для независимых переменных координатами
1
2
3
4
5
6
7
8
9
x1
x2
–
–
+
–
–
+
+
+
– 0
0
+
0 +α
0 –α
0
0
ПФЭ 2 2
звездная точка
центр плана

19. Параметры ортогональных композиционных панов

20. Расчет коэффициентов моделей

Коэффициенты
a1
a2
a3
a4
a5
a6
a7
a8
2
0,11111
0,16667
0,25000
0,30000
0,33333
0,40825
0,50000
0,70711
Число факторов
3
4
0,06667
0,04000
0,09141
0,05000
0,12500
0,06250
0,23041
0,12500
0,25820
0,20000
0,30234
0,22361
0,35355
0,25000
0,48001
0,35355
5
0,03704
0,04811
0,06250
0,07220
0,19245
0,21934
0,25000
0,26870

21. Влияние композицоинности плана

• Если в центре плана поставить не один эксперимент, то может
быть определено такое число точек, что постоянство
информации будет иметь место не только в равноотстоящих от
центра плана точках, но и на большей части отрезка радиусвектора 0 1.
• Информационные контуры для центральных комплексных
планов второго порядка:
Не ротатабельный план
Ротатабельный план
Информационный вектор

22. Пример использования симметричного ортогонального композиционного плана второго порядка

• Изучали механические свойства одного из алюминиевых
деформированных сплавов в зависимости от содержания
лития, температуры и времени старения. В качестве отклика
выбрали предел прочности. По результатам измерений,
проведенных ранее, было установлено, что дисперсия 4, число
степеней свободы 10.
x 2 , t стар. x3 , стар.
x1 , %Li
Факторы
Был реализован ПФЭ
23, по результатам которого рассчитаны
коэффициенты
для линейной модели:
основной уровень K io
1,0
175
4
xi
верхний уровень +1
нижний уровень –1
звездные точки:
=+1,215
= –1,215
0,5
1,5
0,5
25
200
150
2
6
2
1,6
0,4
205
145
6,4
1,6

23.

• Дисперсия в определении коэффициентов:
• Дисперсия неадекватности:
, где
• N- количество опытов.
• K’-количество коэффициентов.
Модель не адекватна

24. Проведем дополнение модели

• В таком случае можно дополнить данную модель звездными
точками и опытами в центре плана.
• Для того, чтобы сделать матрицу планирования ортогональной,
мы должны ввести столбец новой переменной для нахождения
коэффициентов регрессии при квадратичных планах.
• Для 22=0,67; для 23=0,73.

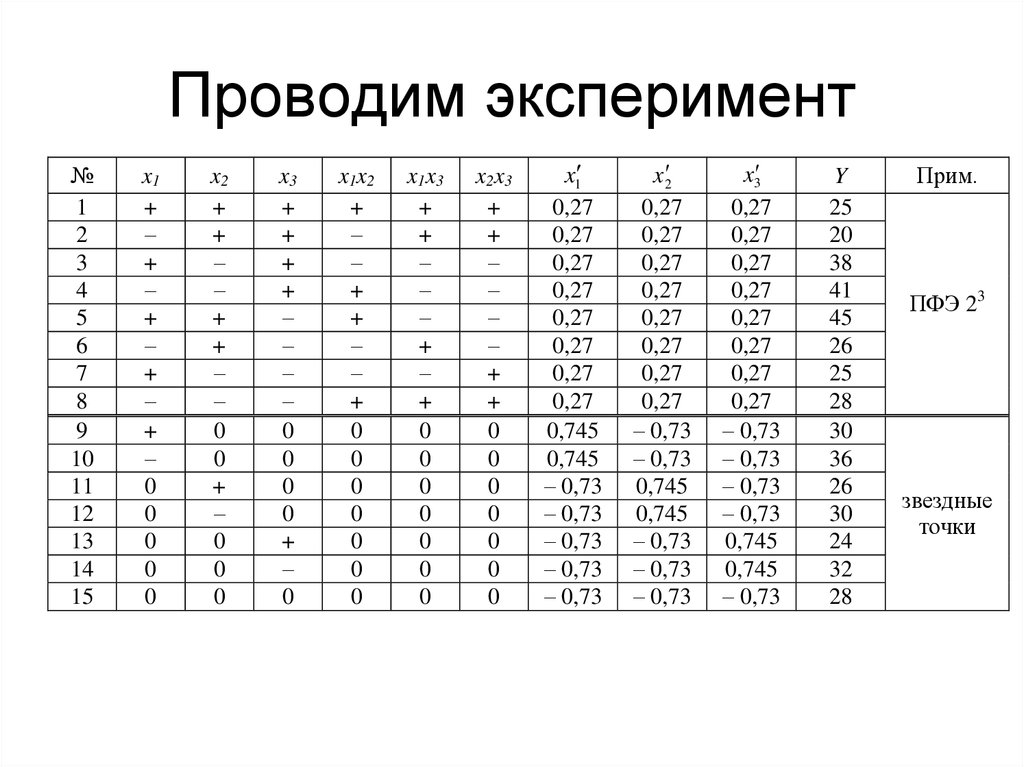
25. Проводим эксперимент

№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
x1
+
–
+
–
+
–
+
–
+
–
0
0
0
0
0
x2
+
+
–
–
+
+
–
–
0
0
+
–
0
0
0
x3
+
+
+
+
–
–
–
–
0
0
0
0
+
–
0
x1x2
+
–
–
+
+
–
–
+
0
0
0
0
0
0
0
x1x3
+
+
–
–
–
+
–
+
0
0
0
0
0
0
0
x2x3
+
+
–
–
–
–
+
+
0
0
0
0
0
0
0
x1
0,27
0,27
0,27
0,27
0,27
0,27
0,27
0,27
0,745
0,745
– 0,73
– 0,73
– 0,73
– 0,73
– 0,73
x 2
0,27
0,27
0,27
0,27
0,27
0,27
0,27
0,27
– 0,73
– 0,73
0,745
0,745
– 0,73
– 0,73
– 0,73
x3
0,27
0,27
0,27
0,27
0,27
0,27
0,27
0,27
– 0,73
– 0,73
– 0,73
– 0,73
0,745
0,745
– 0,73
Y
25
20
38
41
45
26
25
28
30
36
26
30
24
32
28
Прим.
ПФЭ 23
звездные
точки

26.

• По результатам эксперимента, используя коэффициенты
рассчитываем коэффициенты регрессии:
b0 30,27 ; b1 0,98 ; b2 1,91 ; b3 0,89 ; b12 3,75 ; b13 1,75 ;
b23 6,5 ; b11 3,21 ; b22 0,19 ; b33 0,19 .
• По критерию Стьюдента:
b0 t S b0 1,151
bi 1,349 ;
bij 1,577 ;
bii 2,141
• статистически значимыми будут
• Уравнение регрессии:
• Критерий Фишера расчетный
• гипотеза об адекватности модели не отвергается.

27. Некомпозиционные планы

Для системы с двумя независимыми переменными ротатабельными
планами второго порядка будут планы, точки которых являются
вершинами правильного пяти- или шестиугольника. Добавив к этим
точкам центральные точки, можно получить униформно –
ротатабельные планы.
Униформность – это свойство планов, при котором вокруг центра
плана дисперсия предсказаний остается одинаковой.
Понятно, что ротатабельные планы с пяти- и шестиугольниками не
пересекаются с ПФЭ коэффициенты рассчитываются из матрицы
исходных данных.

28. Планы Хартли и Вестлейка

• Ортогональные и ротатабельные центральные композиционные
планы второго порядка строятся на основе матриц ПФЭ 2n (для n <5),
ДФЭ 2n-1 (для n =5) и ДФЭ 2п-2 для (n >8), обеспечивающих взаимно
независимое (несмешанное) определение всех линейных и парных
коэффициентов.
• Планы Хартли для n = 2, 3, 4, 5 могут быть построены на базе
полуреплик соответствующих размерностей; для n = 6 в качестве
линейной основы плана может использоваться 1/4-реплика ДФЭ 26-2.
Очевидно, что разрешающая способность планов Хартли и
Вестлейка должна быть ниже, чем для планов ортогональных или
ротатабельных, однако в ряде практических задач этой
разрешающей способности может оказаться достаточно для
получения удовлетворительной модели исследуемой системы.
Планы Хартли можно сделать почти ортогональными, если в них, как
и в ортогональных центральных композиционных
планах, сделать замену переменных
согласно уравнению:

29.

• звездное плечо определяется по формуле:
N0 – число точек в исходном ПФЭ.
r – число повторений в звездных точках и в центре плана.
N = N0+(2n+1)r – общее число опытов композиционного плана.
Планы Вестлейка дают достаточно хороший результат, если
получается удовлетворительная модель системы. Но все
коэффициенты оказываются взаимно коррелируемыми.
x1 x2 x3 x4 x1 x2 x3
• Линейная основа плана Хартли для п = 4
Это полуреплика 24-1, которую можно
- - + - использовать для построения
+ - - + композиционного плана
- + - - - +
+
+ +
-
+
x4
+
+
+ + +

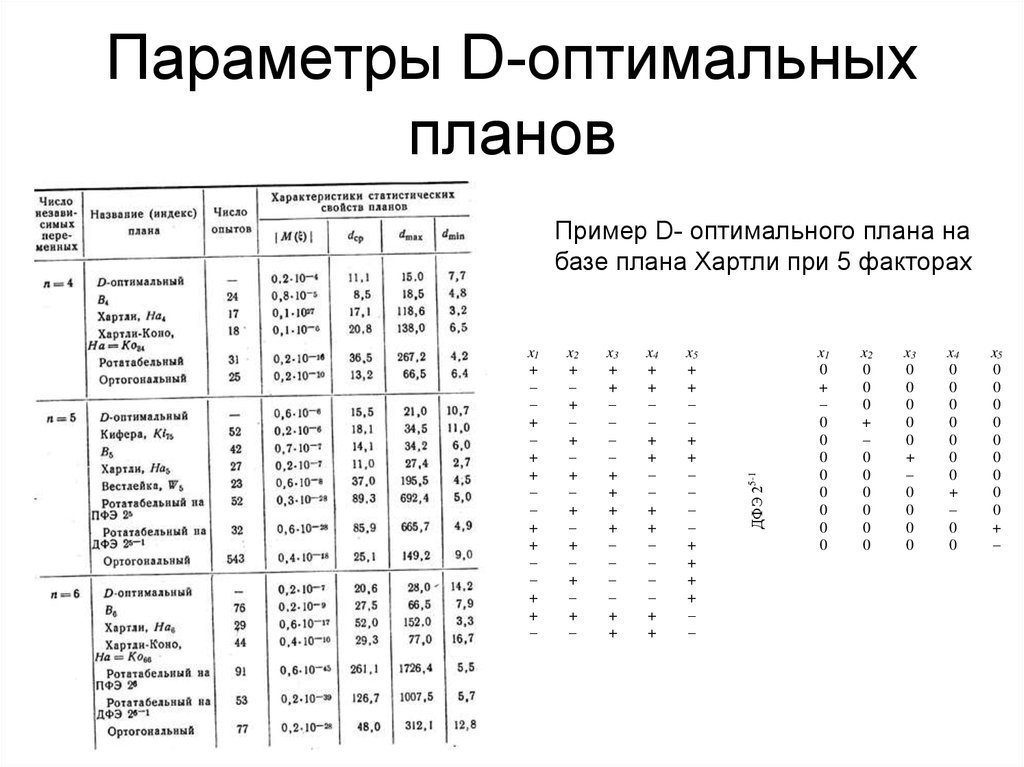
30. Планы близкие к D-оптимальным

• Такие планы имеют минимальный объем эллипсоида ошибок
оценок коэффициентов модели, однако планы эти содержат
практически неприемлемое число экспериментальных точек и
поэтому не применяются.
• Представляют практический интерес планы, содержащие
приемлемое для практического использования число опытов и
близкие по своим статистическим свойствам к D-оптимальным.
В таблице приводятся основные статистические характеристики
некоторых из таких планов.
• В качестве оценки степени D-оптимальности планов используют
обычно величину определителя информационной матрицы
плана, поскольку D-оптимальным планам соответствуют
информационные матрицы с максимальным на всевозможном
множестве планов значением определителя.

31. Параметры D-оптимальных планов

x1
+
–
–
+
–
+
+
–
–
+
+
–
–
+
+
–
x2
+
–
+
–
+
–
+
–
+
–
+
–
+
–
+
–
x3
+
+
–
–
–
–
+
+
+
+
–
–
–
–
+
+
x4
+
+
–
–
+
+
–
–
+
+
–
–
–
–
+
+
x5
+
+
–
–
+
+
–
–
–
–
+
+
+
+
–
–
ДФЭ 25-1
Пример D- оптимального плана на
базе плана Хартли при 5 факторах
x1
0
+
–
0
0
0
0
0
0
0
0
x2
0
0
0
+
–
0
0
0
0
0
0
x3
0
0
0
0
0
+
–
0
0
0
0
x4
0
0
0
0
0
0
0
+
–
0
0
x5
0
0
0
0
0
0
0
0
0
+
–

32. Пример расчета для плана второго порядка

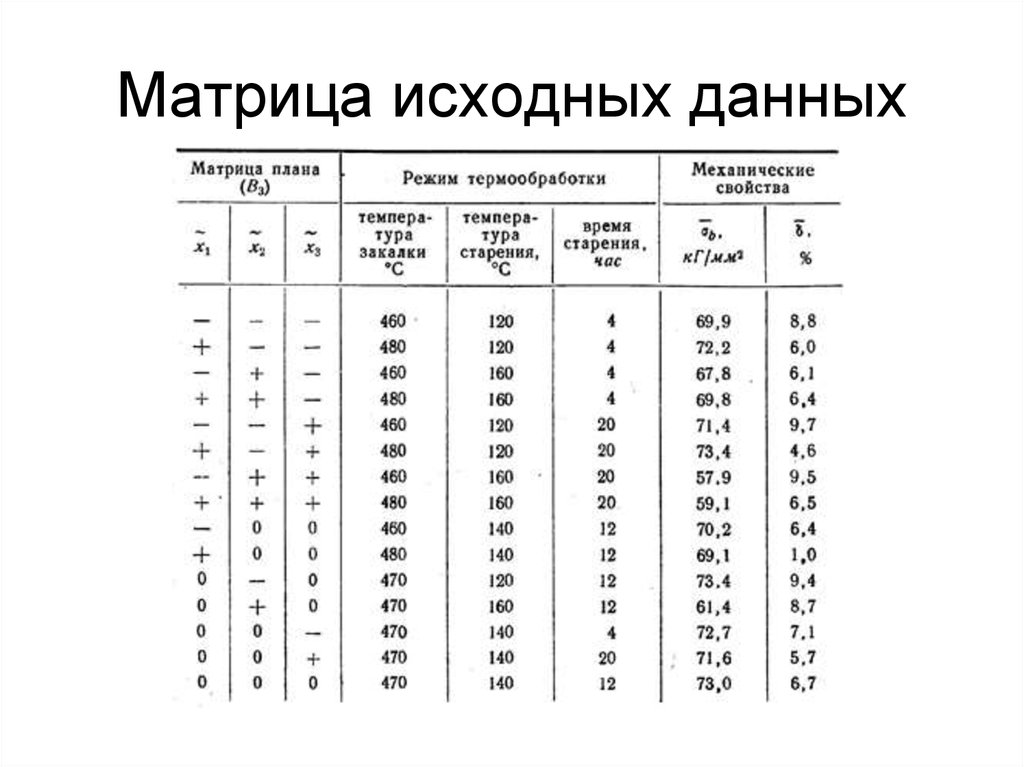
• Для алюминиевого сплава, легированного цинком (10,0-10,5%),
магнием (2,0-2,5%), медью (2,5-3,0%), марганцем (0,4%), титаном
(0,05%) и цирконием (0,13%), проверяли оптимальность (с точки
зрения прочности и пластичности при статическом растяжении)
режима термообработки, применяемого обычно для алюминиевых
высокопрочных сплавов системы Аl—Zn—Mg—Сu: закалка с 465° С
в воде и старение при 140° С, 16 часов.
• Расчет коэффициентов регрессии проводили по общему
уравнению В=(XТ X) -1 XТ Y

33. Матрица исходных данных

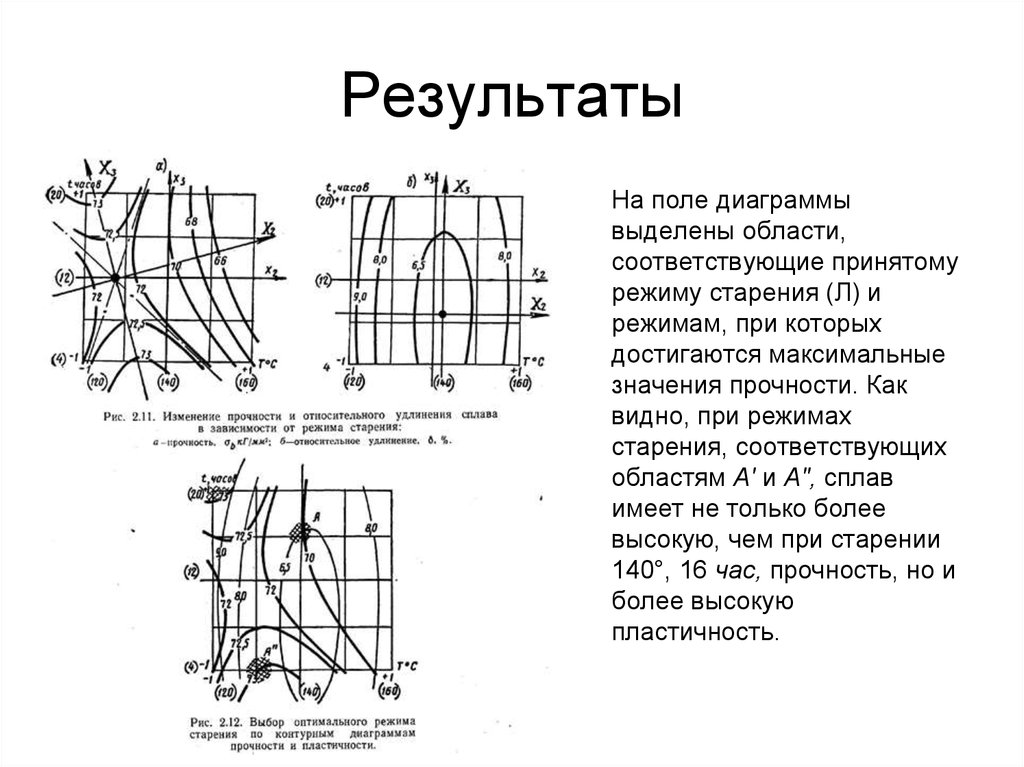
34. Результаты

На поле диаграммы
выделены области,
соответствующие принятому
режиму старения (Л) и
режимам, при которых
достигаются максимальные
значения прочности. Как
видно, при режимах
старения, соответствующих
областям А' и А", сплав
имеет не только более
высокую, чем при старении
140°, 16 час, прочность, но и
более высокую
пластичность.

35. Выводы

• Таким образом, проверяемый режим
термообработки не является оптимальным для
исследуемого сплава.
• На основании полученных результатов в
качестве оптимального был рекомендован режим
старения 120° С, 20 час. Для случаев
применения сплава, когда требования к его
пластичности не являются определяющими, был
рекомендован режим старения 130° С, 4 час,
обеспечивающий достаточно высокий уровень
прочности и пластичности при минимальной
продолжительности процесса старения.