Similar presentations:
Теплопроводность. Нестационарная теплопроводность. (Тема 4. Лекции 16,17)
1. Тема 4. Теплопроводность
Лекции 16, 172. § 4. Нестационарная теплопроводность
Процесс теплопроводности в неограниченной пластинеописывается уравнением:
,2–T
T a
t
x2
одномерное дифференциальное уравнение нестационарной
теплопроводности
при не зависящем от
температуры
и отсутствии внутренних
источников теплоты.
В качестве начальных условий принимаем равномерное
распределение температуры в начальный момент времени. В
качестве граничных условий рассмотрим граничные условия
III рода.
2
3.
Для решения дифференциального уравнениявоспользуемся методом разделения переменных:
T (x, t) = Ф (x) П (t) .
1 dП 1 d 2Ф
dП
d 2Ф
Ф
a П 2
2
dt
dx
a П dt Ф dx
1 dП
2
k
,
a k 2 t ,
П(
t
)
C
exp
a
П
dt
1
2
1 d Ф k 2 .
Ф( x) C cos(k x) C sin(k x).
2
3
Ф
2
dx
T(x, t) exp a k 2 t C cos(k x) D sin(k x),
где С = С1 С2 , D = С1 С3 .
Константы C, D и k определим из краевых условий.
3
4.
Принимаем допущения:1) считаем, что нагрев (или охлаждение) пластины
происходит из-за конвективной теплоотдачи
от окружающей среды с постоянной температурой Т 0;
2) рассматриваем осесимметричную задачу, то есть
граничные условия на обеих поверхностях пластины
считаем одинаковыми.
Т
Т0
Т0
t2
t1
ТН t=0
0
х
Функция sin (k x) является нечетной, следовательно,
для симметричной задачи константа D = 0.
4
5.
Решение принимает вид:T(x, t) C exp k 2 a t cos(k x).
Краевые условия:
Т (x, 0) = TН ,
Т
x x δ .
α Т Т( δ, t) λ
0
Введем новую переменную – избыточную температуру:
(x, t) = T0 – T (x, t) .
Для этой переменной формулировка задачи имеет вид:
2
a
.
t
x2
5
6.
Краевые условия:(x, 0) = T0 – TН = Н ,
α ( δ, t) λ
.
x x δ
Знак в правой части граничного условия изменился
в связи с тем, что
T
x
x .
Решение имеет тот же вид, так как уравнение
теплопроводности имеет тот же вид:
(x, t) C exp k 2 a t cos(k x)
.
6
7.
Подставим решение в граничное условие,например, при x= :
α C exp k 2 a t cos(k δ)
λ C k exp k 2 a t sin(k
δ)
k λ k δ
ctg(k δ)
.
α δ
α
λ
Обозначим произведение k = и назовем
эту величину характеристическим числом.
α δ – критерий Био.
Bi
λ
7
8.
Жан Батист Био (1774–1862) –французский физик, геодезист
и астроном. Его первые работы были
посвящены исследованию свойств газов.
В 1811 г. открыл поляризацию света
при преломлении, в 1815 – круговую
поляризацию и установил закон вращения
плоскости поляризации (закон Био),
существование право- и левовращающих
веществ. В 1820 г. совместно с Феликсом
Саваром открыл закон, определяющий
напряженность магнитного поля
проводника с током (закон Био-Савара).
Био – автор широко известного «Курса
общей физики» (1816). Его идеи
о нематериальности теплоты,
работы по теплопроводности, обработка
математическим путем опытов
над тепловым расширением тел и
многое другое показывают, как он
стремился все части современной ему
физики усвоить
и оформить до
такой степени, что читателю кажется,
будто они являются его оригинальными
открытиями.
8
9.
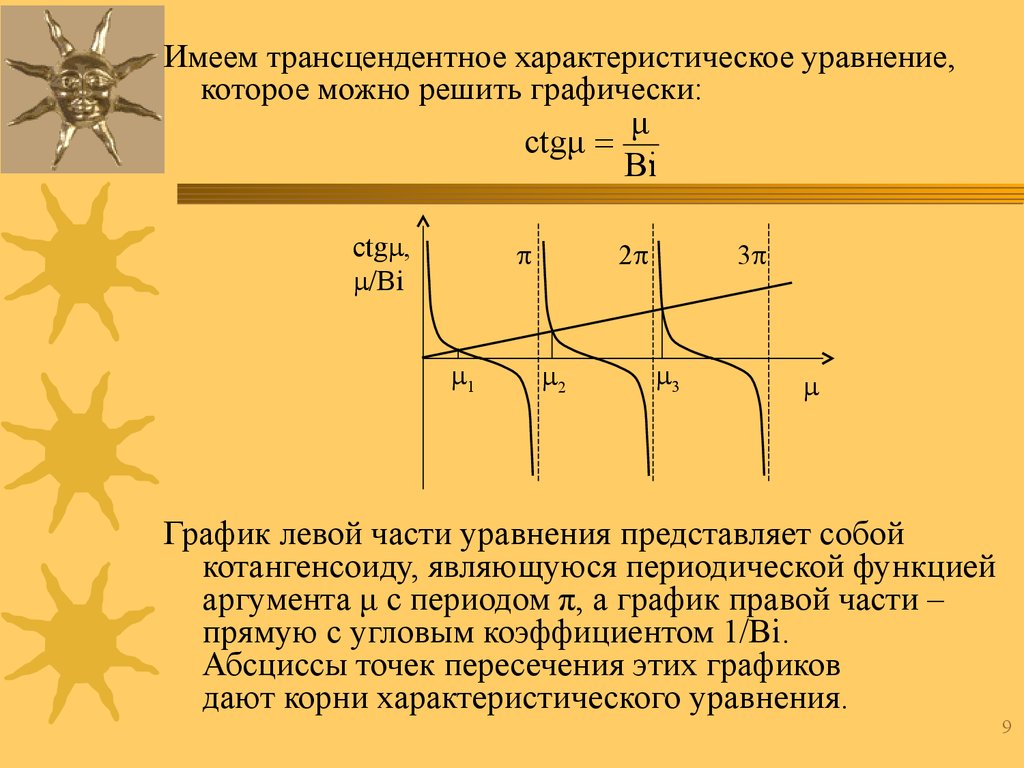
Имеем трансцендентное характеристическое уравнение,которое можно решить графически:
μ
ctgμ .
Bi
ctg ,
/Bi
1
2
2
3
3
График левой части уравнения представляет собой
котангенсоиду, являющуюся периодической функцией
аргумента μ с периодом π, а график правой части –
прямую с угловым коэффициентом 1/Bi.
Абсциссы точек пересечения этих графиков
дают корни характеристического уравнения.
9
10.
Характеристическое уравнение имеет бесчисленноемножество корней.
В связи с линейностью дифференциального уравнения
теплопроводности его общее решение является
суммой его частных решений:
x
2 a t
(x, t) Cn exp μ n 2 cos μ n .
δ
n 1
δ
a t
Стоящая в показателе экспоненты величина δ2 Fo –
критерий Фурье, безразмерное время.
Неизвестные величины Cn определим из начального
условия.
При Fo=0
x
Н Cn cos μ n
δ .
n 1
10
11.
xcos
μ
и
Умножим обе части равенства на
m
δ
проинтегрируем по х в пределах толщины пластины.
Меняя порядок интегрирования и суммирования (ввиду
линейности этих операций) получим выражение:
δ
δ
x
x
Н cos μm dx Cn cos μm x cos μ n dx
δ
δ
δ
n 1
δ
δ
δ
Cn cos2 μn x dx ,
δ
δ
x
x
cos
μ
cos
μ
являются
n
и
поскольку
m
δ
δ
ортогональными функциями, как это следует
из характеристического уравнения. То есть их
произведение обращается в нуль, кроме случая,
когда m = n.
11
12.
Учитывая, что1
cos
a
xdx
sin a, xполучим:
a
δ
δ
x
μn
cos
μ
dx
2
cos
x dx
n
δ
δ
0
δ
δ
μn
δ
δ
.n
2 sin x 2 sinμ
μ
μ
δ 0
n
n
Учтем также, что cos2 a xdx 1 x 1 sin 2a x
4a
2
и sin2x = 2 sinx cosx.
Тогда
δ
δ
x
x
2
cos
μ
dx
2
cos
μ
dx
n
n
δ
δ
0
δ
2
δ
δ
δ
δ
μn
μn
μn
x
sin 2 x x sin x cos x
2 μn
δ 0 μ n
δ
δ
0
δ
δ
.
δ
sinμ n cosμ n
μ sinμ cosμ
n
n
n
μn
μ
n
12
13.
Итак, получаем2 Н sinμ n ,
Сn
μ n sinμ n cosμ n
и решение принимает окончательный вид:
Н
2 sinμ
Н
n
cos μ X exp μ 2 Fo,
n
μ
sinμ
cosμ
n 1 n
n
n
где X x – безразмерная координата.
δ
n
Таким образом, безразмерная избыточная температура
Т0 Т
,
θ
f(Bi, Fo, X)
H Т 0 Т H
где
Bi
– параметр задачи,
Fo и X – безразмерные независимые переменные.
13
14.
Рассмотрим, к чему сводится полученное решениепри Bi 0.
При этом угловой коэффициент 1/Bi прямой на рисунке
графического решения характеристического уравнения
(слайд 9) и прямая совпадает с осью ординат.
n принимает следующий ряд значений: 0, , 2 , 3 …
Все коэффициенты Сn, кроме первого, обращаются
в нуль, а для первого получается неопределенность
типа нуль, деленный на нуль, которую необходимо
раскрыть.
2 sinμ n
Обозначим через Dn
Сn .
μ n sinμ n cosμ n
Раскроем с помощью предельного перехода
неопределенность для D1 при 1 = 0:
lim D1 lim
μ 0
1
μ 0
1
2 sinμ1
2 μ1
1.
μ1 sin μ1 cos μ1 μ1 μ1 1
14
15.
Решение для рассматриваемого случая сводитсяк следующему:
θ cos μ X exp μ 2 Fo .
1
1
Определим конкретный вид связи между 1 и Bi. При
1 0 sin 1 1, tg 1 1, ctg 1 1/ 1. Следовательно,
характеристическое уравнение принимает вид:
1/ 1 = 1/Bi μ1 Bi,
Bi 0
а lim cos ( Bi X) 1, так как 0 Х 1.
Окончательно получим:
= exp( Bi Fo) .
15
16.
Рассмотрим нестационарную теплопроводностьпри граничных условиях I рода для неограниченной
пластины. Считаем, что на границах пластины
происходит конвективная теплоотдача.
При конечных значениях величины полутолщины
пластины и коэффициента теплопроводности случай
Bi означает . Из-за интенсивной теплоотдачи
разность температуры между средой
и
поверхностью объекта T0 – TW = q / 0 (так как
плотность теплового потока q – величина постоянная).
Формулировка задачи:
2
a
;
t
x2
начальное условие: (x, 0) = Н ,
граничное условие: ( ,t) = 0 ,
где = TW – Т – текущая избыточная температура,
Н = TW – ТН – начальная избыточная температура.
16
17.
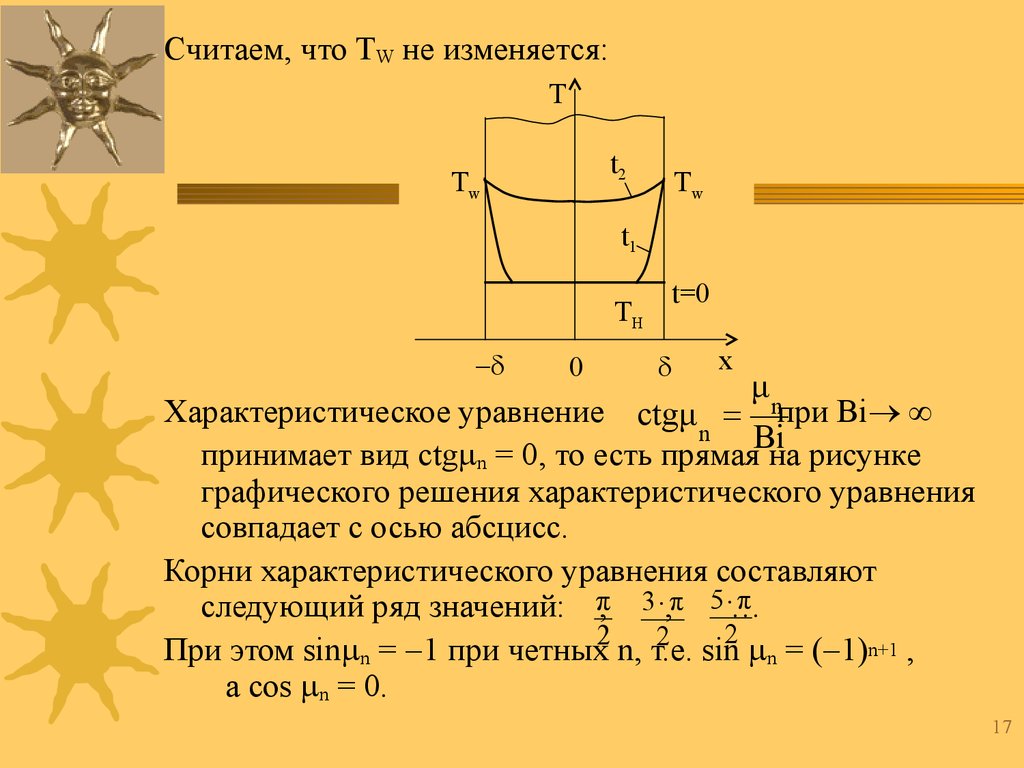
Считаем, что TW не изменяется:Т
t2
Тw
Тw
t1
ТН
0
t=0
х
μn
Характеристическое уравнение ctgμ при Bi
n
Bi
принимает вид ctg n = 0, то есть прямая на рисунке
графического решения характеристического уравнения
совпадает с осью абсцисс.
Корни характеристического уравнения составляют
π
следующий ряд значений: π, 3 ,π 5 …
2
2
При этом sin n = 1 при четных2 n, т.е.
sin n = ( 1)n+1 ,
а cos n = 0.
17
18.
Выражение для безразмерной избыточной температуры2 sinμ
n
θ
cos μ X exp μ 2 Fo
n
n
μ
sinμ
cosμ
n 1
H
n
n
n
(решение задачи нестационарной теплопроводности
при граничных условиях III рода, см. слайд 13)
принимает вид:
2 ( 1) n 1
θ
cos μ X exp μ 2 Fo
n
n
.
μ
n 1
n
В данном случае относительная избыточная температура
определяется как функция числа Фурье
и безразмерной координаты = f (Fo, X).
Число Био не является параметром задачи, так как
лимитирующим звеном в процессе теплообмена
является внутренний теплообмен.
18
19. § 5. Регулярный тепловой режим
В переходных процессах нестационарнойтеплопроводности, когда температура в каждой точке
тела изменяется от одного установившегося значения
до другого, можно выделить три характерных режима:
• неупорядоченный, при котором начальное
распределение температуры оказывает заметное
влияние на развитие процесса;
• регулярный, когда влияние начального распределения
температуры исчезает;
• стационарный, при котором температура
во всех точках тела становится равной температуре
окружающей среды.
19
20.
Ряд решения задачи нестационарной теплопроводностииз § 17 быстро сходится.
Во-первых, каждое следующее характеристическое число
больше предыдущего, k > k+1, и n стоит в квадрате
в отрицательном показателе экспоненты.
Во-вторых, поскольку критерий Фурье тоже стоит
в отрицательном показателе экспоненты, ряд
сходится тем быстрее, чем больше времени прошло с
начала процесса. Практически уже при Fo 0,3 сумма
ряда равна его первому слагаемому:
2 sinμ1
θ
cos μ X exp μ 2 Fo ,
1
1
μ1 sinμ1 cosμ1
π
где 1 = f (Bi), 0 ≤ 1 ≤ 2 .
20
21.
2 sinμ1Обозначим D1
μ1 sinμ1 cosμ1
и прологарифмируем последнее выражение:
a t
lnθ ln D1 cos μ1 X μ12 2 .
δ
ln
ln 1
ln 2
tР
t1
t2
t
tР – время наступления регулярного режима.
lnθ1 lnθ 2
m
постоянная
t 2 t1 – темп охлаждения (нагрева),
–1
скорость изменения ln , с .
2 a
m
μ
1 2 .
Очевидно, что
δ
21
22.
Для граничных условий I рода при Fo 0,3 1 =π
2.
π2 a
m
4 δ2
Величина
называется темпом нагрева (охлаждения)
при граничных условиях I рода. Итак, в этом случае
темп нагрева пропорционален коэффициенту
температуропроводности:
m∞ = k a ,
π2
где k
– коэффициент формы для плоской пластины.
4 δ2
Таким образом, при граничных условиях I рода темп
нагрева не зависит от критерия Био, поскольку нагрев
(охлаждение) тела лимитируется только внутренним
теплообменом.
22
23.
Закономерности регулярного теплового режимаиспользуют для экспериментального определения
теплофизических свойств различных материалов
и коэффициента теплоотдачи.
Для этого необходимо снять кривую изменения
температуры в какой-либо точке тела и, представив
ее в координатах ln –t, найти тангенс угла наклона
прямолинейного отрезка зависимости к оси времени.
m
a
Теперь, зная форму и размер тела, можно найти
k .
Тогда коэффициент теплопроводности = a c .
Затем, уменьшив интенсивность внешнего
теплопереноса, надо организовать теплообмен
с граничными условиями III рода, и найти m,
зависящий в данном случае от 1 и Bi.
Bi λ
α
Наконец, находят коэффициент теплоотдачи:
δ .
23





















 physics
physics








