Similar presentations:
Нестационарная теплопроводность цилиндра конечных размеров
1.
2.
Национальный исследовательский университет «МЭИ»Нестационарная
теплопроводность цилиндра
конечных размеров
Специальность 14.03.01 «Ядерная энергетика и теплофизика»
Группа: ТФ-12-18
Студенты: Пронин Богдан
Шелухин Андрей
3.
Актуальность работыС расчётами нагревания и охлаждения тел часто
приходится иметь дело в различных отраслях. В этом
случае основным рабочим режимом является
нестационарный, при котором определяют время,
необходимое для прогрева или охлаждения материала до
необходимой температуры, или температуру, до которой
происходит нагрев (охлаждение) в течение известного
промежутка времени. В данной работе мы рассмотрим
пример нестационарной теплопроводности в
перевозимой автоцистерне наполненной водой при
отрицательной температуре окружающей среды.
4.
Цель работыПоказать общие особенности
нестационарных процессов, познакомиться с
методом решения задач нестационарной
теплопроводности и получить математические
соотношения для практических расчётов, а также
применить полученные навыки расчётов для
решения задачи нестационарной
теплопроводности для цилиндра конечных
размеров.
5.
Постановка задачиВ качестве практического примера подобной задачи
представим ситуацию, когда в сильные заморозки
необходимо перевести или хранить значительный объём
воды в автоцистерне. В расчёте мы принимаем форму
цистерны за идеальный цилиндр конечных размером.
Будут рассмотрены два случая для цистерн разных
размеров. Обе цистерны имеют диаметр 2500 мм и
изготовлены из материала марки Сталь 09Г2С. Отличие
цистер для двух случаев залючается в том, что в первом
случае длинна цистерны 9000 мм, а во втором 4500 мм.
Итогом расчётов будет вынесение графиков
температурного состояния воды в цистерне через
определённое время, а так же сравнение полученных
зависимостей
6.
Теоретические данныеДля пластины:
( ) C1 exp( ak 2 )
2
a 2
x
( x) C2 sin( kx ) C3 cos( kx)
при 0 0 t0 t ж
при x 0 ( x) x 0 0
при x ( x) x
x
f ( x, ) ( x) ( )
/ ( ) ak 2 ( ) 0
//
2
( x) k ( x) 0
( x, ) C2 sin( kx) C3 cos( kx) C1 exp( ak 2 )
x
a
An cos( n ) exp( n2 2 )
n 1
2 sin n
An 0
n sin n cos n
t tж
2 sin n
cos( n X ) exp( n2 Fo)
t 0 t ж n 1 n sin n cos n
7.
Для цилиндра:2 1
a 2
r r
r
Число Био и критерий Фурье
Bi
1
при 0 0 t0 t ж
Fo
при x 0 ( r ) x 0 0
при x r0 ( r ) x r0
x r0
f (r , ) ( x) ( )
......
t tж
2 J1 ( n )
J 0 ( n ) exp( n2 Fo)
2
2
t 0 t ж n 1 n J 0 ( n ) J1 ( n )
a
2
2
a
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
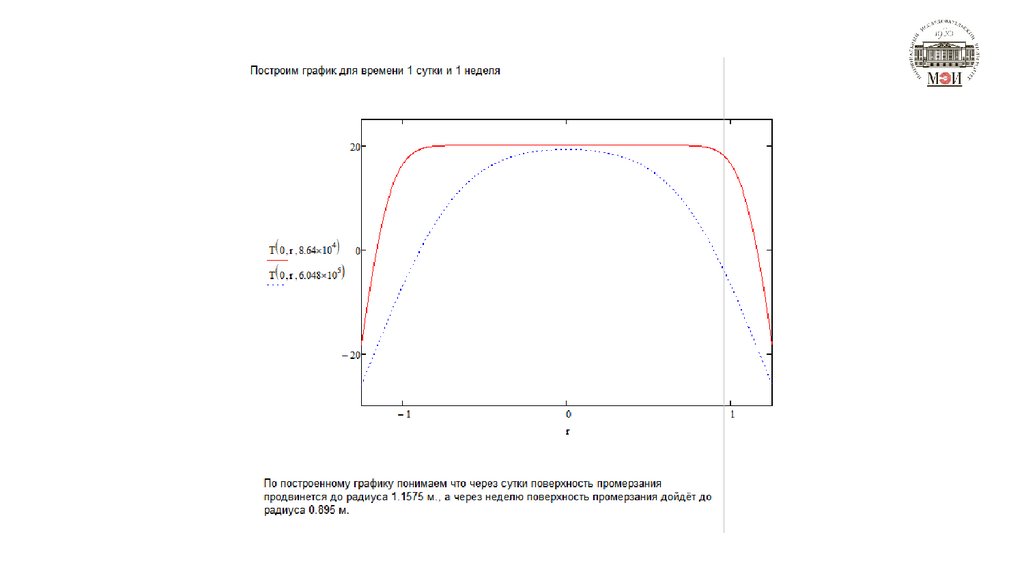
ЗаключениеПо полученным в ходе вычислений данным мы можем сделать
ввод что промерзание таких больших объёмов требует очень много
времени.
Так же исходя из расчётов можно утверждать что изменение
длинны цилиндра практически не влияет на перпендикулярную
оси цилиндра скорость перемещения поверхности промерзания.
Стоит отметить что уже через 90 минут в типовой
автоцистерне началось бы образование льда при заданных
условиях, что могло бы привести к повреждению оболочки.
Так же были закреплены навыки программирования задач для
решения задач нестационарной теплопроводности.


















 physics
physics








