Similar presentations:
Равновесие системы тел. Лекция 4
1. Новосибирский Государственный Архитектурно- Строительный Университет (Сибстрин)
Новосибирский Государственный АрхитектурноСтроительный Университет (Сибстрин)Лекция 4.
РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ
Теория – это некоторым образом
квинтэссенция практики.
Людвиг Больцман
Кафедра теоретической механики
2.
Людвиг Больцман1844-1906, Вена-Линц-Грац-ВенаЛейпциг-Мюнхен-Вена-Дуино
2
3.
2а4. На предыдущей лекции
• Была доказана самая важная теоремастатики, универсально решающая
первую ее задачу
• Были установлены условия
равновесия и выведены уравнения
равновесия
• Введено понятие главного момента и
главного вектора системы сил
3
5. Равнодействующая СПС
Напредыдущей лекции
Равнодействующая
СПС
• Было показано, что для плоской системы сил (все силы находятся
в плоскости Oxy) имеем три уравнения равновесия. Эти уравнения
можно использовать в трех разных формах
Основная форма уравнений равновесия ПСС
n
F
i 1
ix
0,
n
F
i 1
iy
0,
M А ( Fi ) 0
n
i 1
Вторая форма уравнений равновесия ПСС (АВ
M А ( Fi ) 0,
n
i 1
M В ( Fi ) 0,
n
i 1
n
F
i 1
ix
Ox)
0
Третья форма уравнений равновесия ПСС (точки А, В, С не
должны лежать на одной прямой)
n
n
n
M А ( Fi ) 0, M В ( Fi ) 0, M С ( Fi ) 0
i 1
i 1
3.3. ЦЕНТР СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ
i 1
4
6. Цель лекции
• Расчет плоской фермы• Расчет составной конструкции
План лекции
4.1. Определение плоской фермы
4.2. Расчет плоской фермы
4.3. Расчет составных конструкций
4.3.1. Двухсоставная рама
4.3.2. Стержневая конструкция
4.4. Заключение
5
7. 4.1. Плоская ферма
68. 4.1.1. Мотивация
Металлическиекаркасы
Опоры
Мосты
ЛЭП зданий
2.1.
ССС
4.1. ОПРЕДЕЛЕНИЕ
ПЛОСКАЯ ФЕРМА
7
9. 4.1.2. Определение
Ферма – жесткая, геометрически неизменяемая
конструкция, состоящая из невесомых прямолинейных
стержней, соединенных идеальными (без трения)
шарнирами
Шарнирные соединения называются узлами фермы
Плоской называется ферма, все стержни и шарниры
которой лежат в одной плоскости
C
1
A
4
E
3
5
6
2
D
2.1.
ССС
4.1. ОПРЕДЕЛЕНИЕ
ПЛОСКАЯ ФЕРМА
8
B
7
9
G
Уз л ы ф е рм ы буд е м
обозначать большими
латинскими буквами
A, B, … G
Стержни пронумеруем
8
10. 4.1.3. Усилия в стержнях фермы
RA
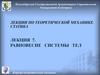
Предполагается, что все усилия приложены к узлам фермы.
В этом случае все стержни будут испытывать только
продольные нагрузки
• Действительно, рассмотрим
равновесие стержня АВ
F
FA 2 A1
• Системы сил, приложенные к узлам,
FB1
– это ССС и их можно заменить
равнодействующими
A
FB 2
• Согласно аксиоме 1, для равновесия
FAn
B
тела необходимо, чтобы
силы
и RB были равны R A
F R
Bn
B
Т.о., эти равнодействующие силы образуют уравновешенную
систему сил и, следовательно, направлены вдоль стержня
2.1.
ССС
4.1. ОПРЕДЕЛЕНИЕ
ПЛОСКАЯ ФЕРМА
9
11. Расчет ферм
Статически определимые фермыРасчет4.1.4.
ферм
• Мы будем рассчитывать ферму без лишних стержней. Ее
можно построить присоединяя к треугольной конструкции
последовательно по два стержня и шарниру
YA
A
Лишний
стержень
XA
RB
B
• У плоских статически определимых ферм число
неизвестных опорных реакций должно равняться трем
• Число стержней плоской статически определимой
фермы определяется формулой
k = 2n – 3,
где k – число стержней, n – число узлов
СТАТИЧЕСКИ
ОПРЕДЕЛИМЫЕ ФЕРМЫ
4.1. ПЛОСКАЯ ФЕРМА
10
12. 4.2. Расчет плоской фермы
1113. 4.2.1. Требования к расчету
Расчет плоской фермы сводится кнахождению сил реакции опор
определению усилий в стержнях
фермы методом вырезания узлов
и/или методом сечений ( Риттера)
2.1.
ССС
4.2. ОПРЕДЕЛЕНИЕ
РАСЧЕТ ПЛОСКОЙ
ФЕРМЫ
12
14. Определение реакций опор фермы
4.2.2. Определениеопорных
реакций
Определение
реакций
опор
фермы
Дана плоская ферма, образованная
y
F3
YA
A
F2
XA
одинаковыми равнобедренными
треугольниками, к узлам которой
параллельно оси x приложены силы
F1 = F2 = F3=2 кН
Освободимся от связи в точке А и
заменим ее реакциями
B
x
• Освободимся от связи в точке В и
заменим ее реакцией
• Запишем уравнения равновесия для плоской системы сил
R
F1 B
F
F
m
a
ix
0, F1 F2 F3 X A 0,
iy
0, RB YA 0,
YA 3 кН
0, F1 2a F2 a RB 2a 0.
X A 6 кН
i
i
A
i
2.1.
ССС
ПРИМЕР
РАСЧЕТА
ФЕРМЫ
4.2. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
ПЛОСКОЙ
ФЕРМЫ
RB 3 кН
13
15. Метод вырезания узлов
4.2.3. узловМетод вырезания узлов
Метод вырезания
y
F3
III
6 IV
F2
4
II
5
7
3
1
VI
R
B
2
F1
I
B
YA
8
A
9
a
x
V XA
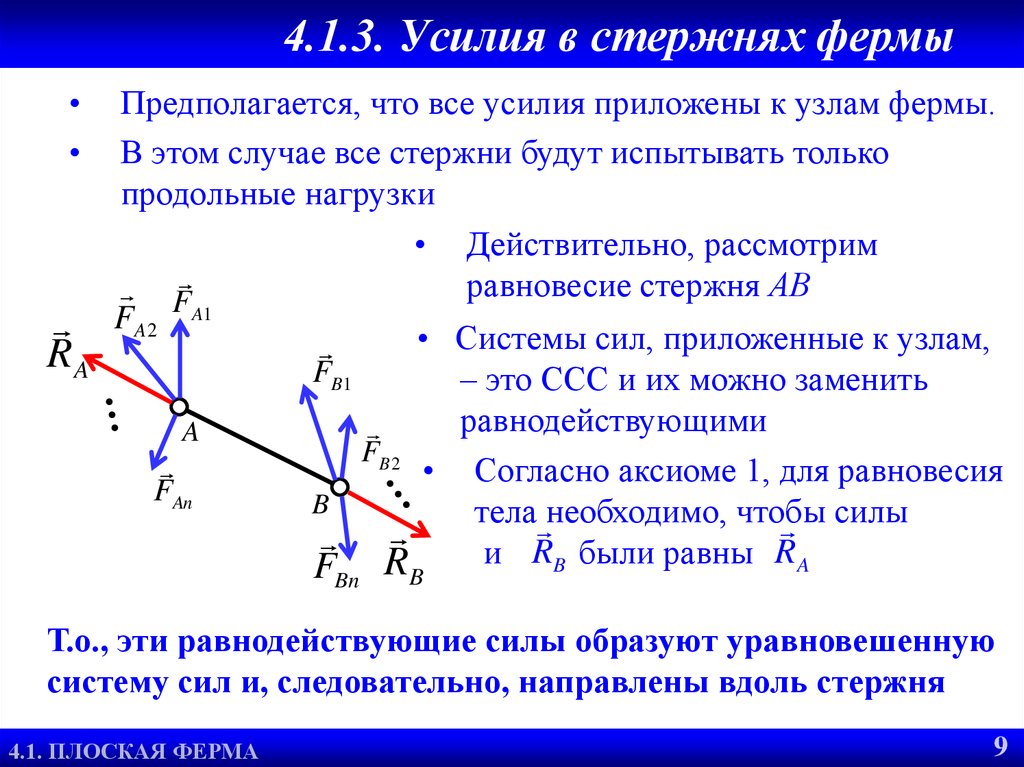
• Пронумеруем все стержни
фермы арабскими цифрами:
1, 2, 3, … 9
• Пронумеруем узлы фермы
римскими цифрами: I, II,…, IV
• Рассмотрим равновесие каждого
узла и составим для него уравнения
равновесия, cчитая условно все
стержни растянутыми и направляя
реакции шарниров от узлов
• Следует учесть, что стержни находятся в равновесии,
поэтому реакции соединительных шарниров должны быть
равны по величине и противоположно направлены
2.1.
ССС
ПРИМЕР
РАСЧЕТА
ФЕРМЫ
4.2. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
ПЛОСКОЙ
ФЕРМЫ
14
16. Метод вырезания узлов
4.2.4. Определениеусилий
в стержнях фермы
Метод
вырезания
узлов
Расчет следует начинать с узла, в котором
сходятся два стержня с неизвестными
усилиями (узел V)
Узел V
YA
XA
8
S8 9
S9
Узел
IV '
S 6 S8
S7
S4
S6 '
i
Y
S
sin
45
0
F
0
:
iy
A
9
y
YA
III 6 IV 8 V
4
7
A
5
XA
9
II 3
1 VI a
RB 2
x
IB
i
Fix 0 :
i
S8' S6 0, S8' S8
Fiy 0 :
S7 0
i
Fix 0 : S
Узел
III
F3
F
0
:
X
S
S
cos
45
ix
A
8
9
F3
F2
0 F1
S5
'
6
F3 S5 cos 45o 0, S 6' S 6
i
S
S
sin
45
0
Fiy 0 : 4 5
i
2.1.
ССС
ПРИМЕР
РАСЧЕТА
ФЕРМЫ
4.2. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
ПЛОСКОЙ
ФЕРМЫ
15
17. Метод вырезания узлов
4.2.4. ОпределениеМетод
вырезанияусилий
узловв стержнях фермы
Узел II
S
F2 4 S3
S1
Узел I
F1 RB
'
S1
S2
Fix 0 : F2 S3 0
i
Fiy 0 :
S4 S1 0
i
Fix 0 :
F3
F2
F1
y
YA
III 6 IV 8 V
4
7
A
5
XA
9
II 3
RB 1 2 VI a
x
IB
F1 S2 cos 45 0
i
'
'
S
R
S
sin
45
0
,
S
F
0
:
1
B
2
1 S1
iy
i
Узел VI
S3
S5 S 7
S2
S9
S
S
cos
45
S
cos
45
S
cos
45
0
F
0
:
3
2
5
9
ix
i
S
S
sin
45
S
sin
45
S
sin
45
0
5
9
Fiy 0 : 7 2
i
2.1.
ССС
ПРИМЕР
РАСЧЕТА
ФЕРМЫ
4.2. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
ПЛОСКОЙ
ФЕРМЫ
16
18.
4.2.5. Методсечений (Риттера)
Метод сечений
(Риттера)
y z
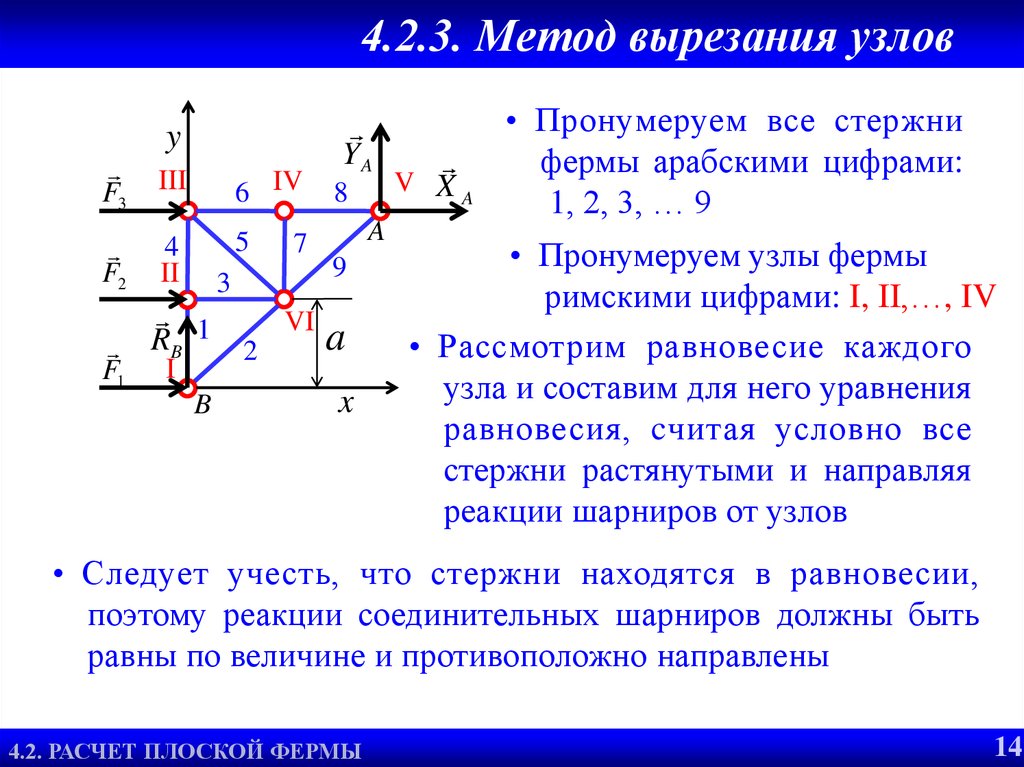
• Метод Риттера удобен, если
необходимо определить усилия в F3
6 IV
каких-то отдельных стержнях
5
7
4
фермы, например, 6, 7, 9
F2
3
• Число стержней в с ечении
VI
R 1
должно быть не более трех
2
F B
YA
V
8
XA
A
9
z
a
1
B
x
Последовательность действий
• Проведем сквозное сечение z–z через стержни 6,7,9
• Пользуясь принципом отвердевания, рассмотрим равновесие
одной из частей фермы, например, правой
• Составляем 3 уравнения равновесия для этой части фермы
2.1.
ССС
ПРИМЕР
РАСЧЕТА
ФЕРМЫ
4.2. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
ПЛОСКОЙ
ФЕРМЫ
17
19.
4.2.5. Метод сечений (Риттера)YA
y z
6 IV
V
S6 7 A
S7
9 S9
VI
XA
z
m 0 : S7 0
A
i
m 0 : aYA aS9 sin 45 0
IV
i
m 0 : a Y A a S6 a X A 0
VI
i
• Решив систему уравнений, находим усилия в стержнях 6,7,9
• Полученные результаты можно использовать для проверки
усилий, определенных методом вырезания узлов
• Если усилия в стержне получилось со знаком « », то
стержень не растянут, а сжат
2.1.
ССС
ПРИМЕР
РАСЧЕТА
ФЕРМЫ
4.2. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
ПЛОСКОЙ
ФЕРМЫ
18
20. 4.3. Расчет составных конструкций
1921. 4.3.1. Примеры составных конструкций
Детскаякроватка
Сборный производственный модуль
1-ый панельный дом Новосибирск, 1960 г.
Деревянные
строительные
Дмитровский
мост,
Новосибирск, конструкции
1971-1780 гг.
2.1.
ССС КОГСТРУКЦИЙ
4.3. ОПРЕДЕЛЕНИЕ
РАСЧЕТ СОСТАВНЫХ
20
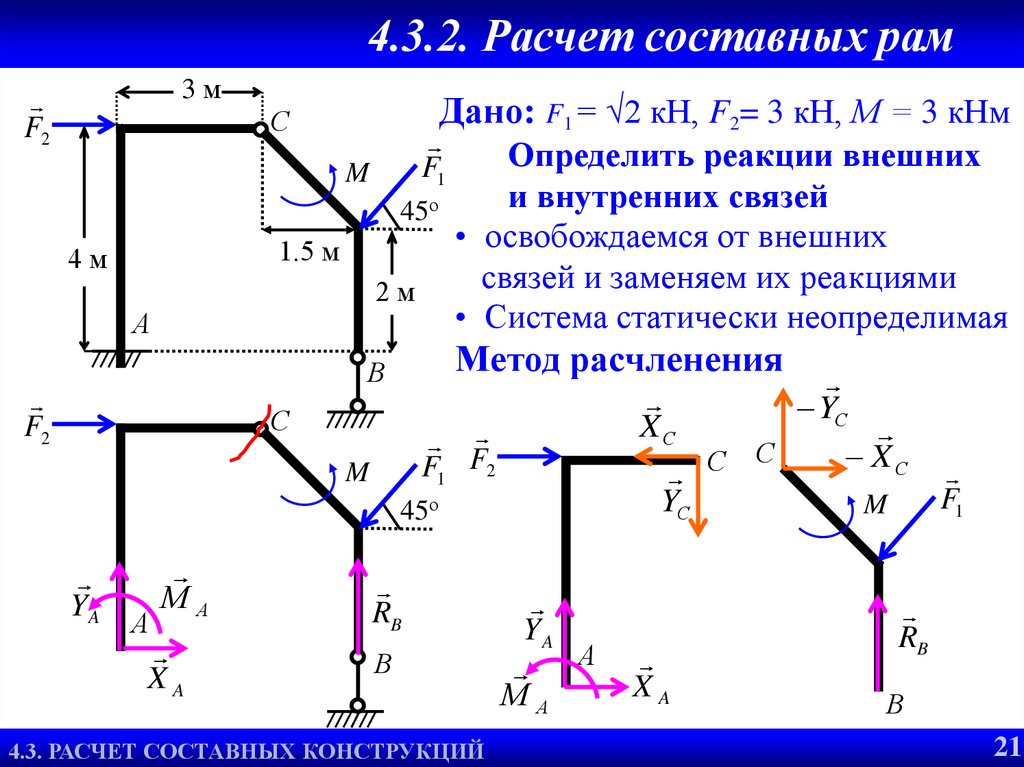
22. 4.3.2. Расчет составных рам
3мF2
Дано: F1 = √2 кН, F2= 3 кН, М = 3 кНм
С
M
1.5 м
4м
А
F1
Определить реакции внешних
и внутренних связей
45о
• освобождаемся от внешних
связей и заменяем их реакциями
2м
• Система статически неопределимая
Метод расчленения
В
F2
С
YС
XС
С
XС
С
F1
YС
M
F1 F2
M
45о
YA
А
МА
XA
RB
В
2.1.
ССС КОНСТРУКЦИЙ
4.3. ОПРЕДЕЛЕНИЕ
РАСЧЕТ СОСТАВНЫХ
YA
А
МА
XA
RB
В
21
23. 4.3.3. Расчет составных рам
YСС
XС
Метод расчленения
F1
M
Fix 0 :
i
Fiy 0 :
X С F1 cos 45o 0
YС F1 cos 45o RB 0
i
m
С
RB
0 : М 1.5RB 2F1 cos 45o 1.5F1 sin 45o 0
i
ВX
С
F2
С
YС
YA
МА
А
XA
F 0:
ix
i
F 0:
iy
F2 Х С Х А 0
YА YС 0
i
m
А
0:
i
2.1.
ССС КОНСТРУКЦИЙ
4.3. ОПРЕДЕЛЕНИЕ
РАСЧЕТ СОСТАВНЫХ
4F2 4 Х С 3YС М А 0
22
24.
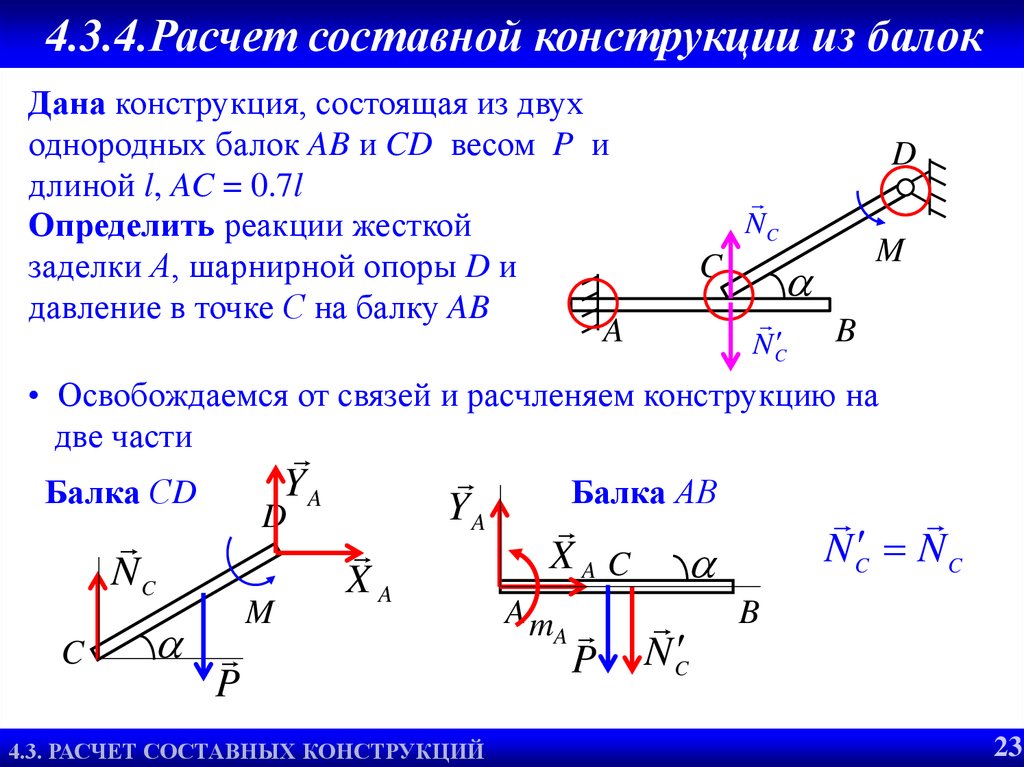
4.3.4.Расчет составной конструкции из балокДана конструкция, состоящая из двух
однородных балок AB и CD весом P и
длиной l, AC = 0.7l
Определить реакции жесткой
заделки А, шарнирной опоры D и
давление в точке С на балку AB
A
D
NC
M
C
N C
B
• Освобождаемся от связей и расчленяем конструкцию на
две части
YA
Балка СD
D
NC
C
M
XA
YA
P
2.1.
ССС КОНСТРУКЦИЙ
РАСЧЕТ
СОСТАВНЫХ
4.3. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
СОСТАВНЫХ
КОНСТРУКЦИЙ
Балка АВ
XA C
Am
A
P
N C N C
N C
B
23
25.
4.3.4.Расчет составной конструкции из балокБалка AB
y
YA
P
Балка СD
y
C
ix
i
XA C
Am
A
F 0: XA 0
F 0 : YA N C P 0
m 0 : mA P 0.5 l N C 0.7 l 0
iy
i
x
NC
YD
B
A
i
F 0: XD 0
ix
i
Fiy 0 : YD N C P 0
XD i
M
mD 0 : M P 0.5l cos
x
i
N C l cos 0
P
NC
D
Находим реакции связей:
2.1.
ССС КОНСТРУКЦИЙ
РАСЧЕТ
СОСТАВНЫХ
4.3. ОПРЕДЕЛЕНИЕ
РАСЧЕТ
СОСТАВНЫХ
КОНСТРУКЦИЙ
X A , YA , mA , N C , X D , YD
24
26. 4.4. Заключение
27. 5.4.1. Основные выводы
На данной лекции Вы овладелиосновными методами расчета
• плоских ферм
• двухсоставных конструкций
• пользуясь этими методами легко
ра с сч и т ыват ь и ко н с т ру к ц и и ,
состоящие из произвольного числа
элементов
5.4.ОСНОВНЫЕ
ЗАКЛЮЧЕНИЕ
ЗАКЛЮЧЕНИЕ
1.2.
ПОНЯТИЯ И МОДЕЛИ
25
28. 4.4.2. Тема следующей лекции
Центр тяжестиРавновесие при наличии
трения
1.3.
СТАТИКИ
4.4.АКСИОМЫ
ЗАКЛЮЧЕНИЕ
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ И МОДЕЛИ
26
29. После лекции
Ни страны, ни погоста не хочувыбирать.
На Васильевский остров
я приду умирать.
Твой фасад темно-синий
я впотьмах не найду,
между выцветших линий
на асфальт упаду.
Иосиф Бродский
1940-1996
«Я думаю, что не человек
пишет стихи, а предыдущее
с ти хотворе н ие пи ше т
следующее»
1.3.
СТАТИКИ
4.4.АКСИОМЫ
ЗАКЛЮЧЕНИЕ
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ И МОДЕЛИ
И душа, неустанно
поспешая во тьму,
промелькнет над мостами в
петроградском дыму,
и апрельская морось,
под затылком снежок, и
услышу я голос:
-- До свиданья, дружок.
И увижу две жизни
далеко за рекой,
к равнодушной отчизне
прижимаясь щекой,
-- словно девочки-сестры
из непрожитых лет,
выбегая на остров,
машут мальчику вслед.
27
























 physics
physics