Similar presentations:
Строительная механика
1. СТРОИТЕЛЬНАЯ МЕХАНИКА
2. I. ОСНОВЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА
(напоминание)3.
1. Основные понятия4.
СилаФундаментальным понятием механики является сила. Действие силы на тело характеризуется величиной или модулем силы, местом приложения и направлением действия.
Линия действия силы
Сила
F
линия действия силы
Прямая, вдоль которой действует сила, называется линией
действия силы.
5.
СилаФундаментальным понятием механики является сила. Действие силы на тело характеризуется величиной или модулем силы, местом приложения и направлением действия.
Линия действия силы
Сила
Сила – количественная мера механического
взаимодействия тел
6.
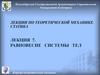
СилаХарактер механического взаимодействия определяет третий закон Ньютона
2
Сила, с которой человек
действует на тело
Сила, с которой тело
действует
на человека
F2
F1
F1= - F2
1
Два тела взаимодействуют с силами, равными по
модулю и действующими по одной прямой в
противоположные стороны
7.
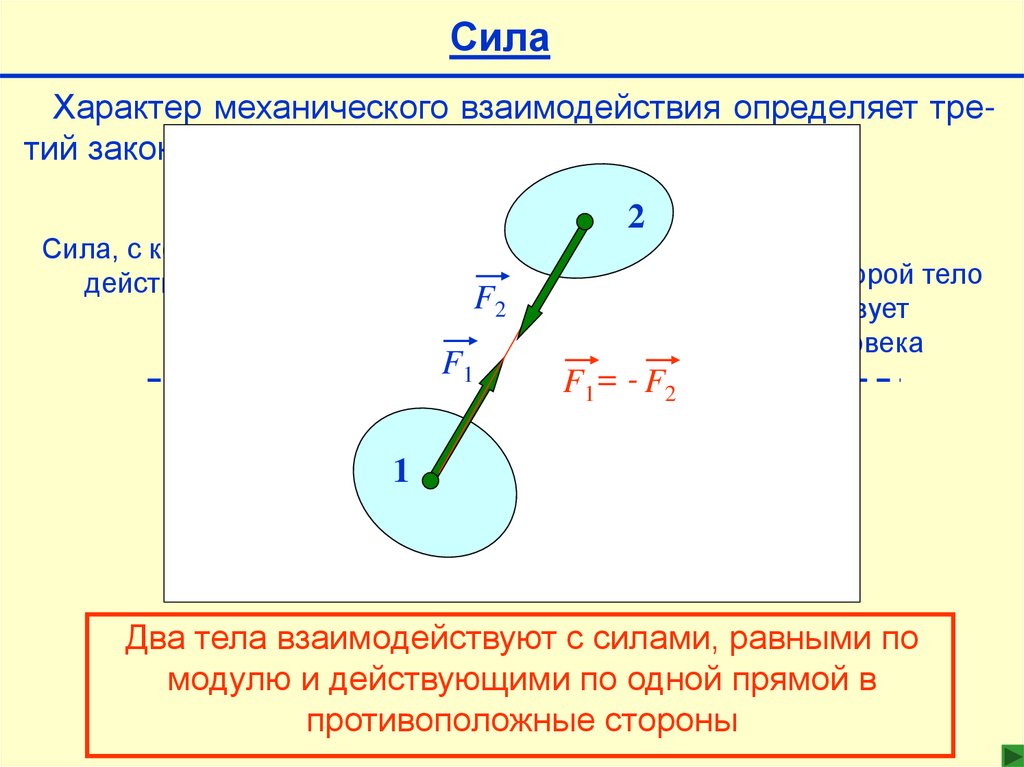
СилаХарактер механического взаимодействия определяет третий закон Ньютона
Сила, с которой человек
действует на тело
Сила, с которой тело
действует
на человека
Два тела взаимодействуют с силами, равными по
модулю и действующими по одной прямой в
противоположные стороны
8.
Свободные и несвободные тела. СвязиСВОБОДНОЕ ТЕЛО
9.
Свободные и несвободные тела. Связи10.
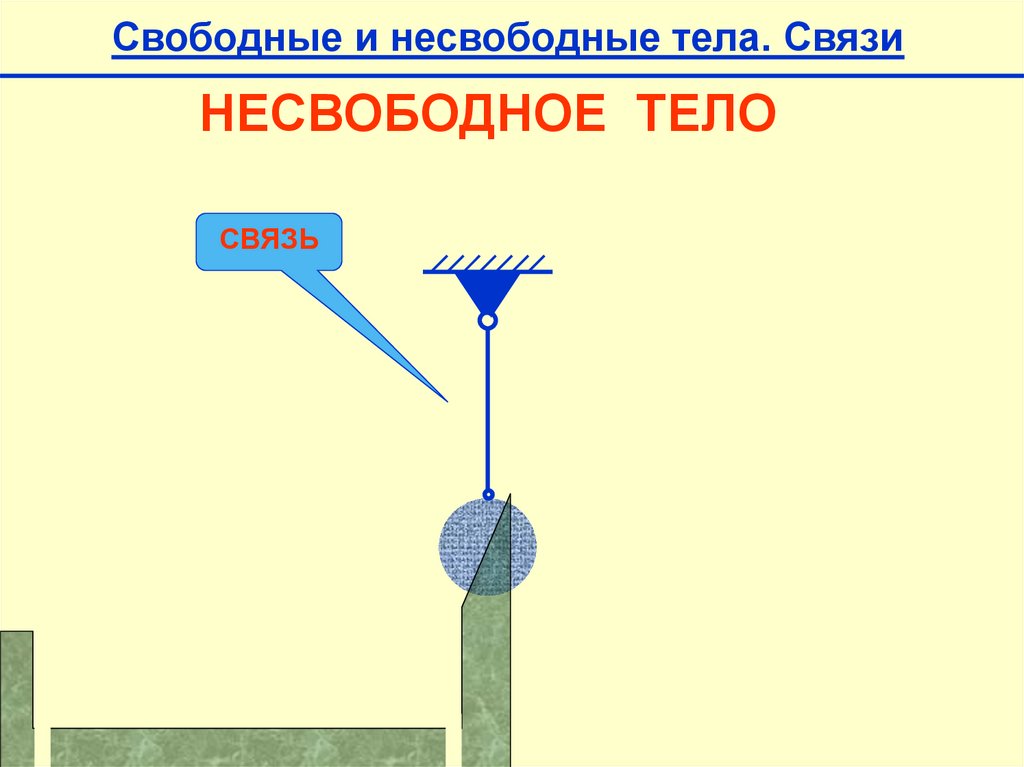
Свободные и несвободные тела. СвязиНЕСВОБОДНОЕ ТЕЛО
СВЯЗЬ
11.
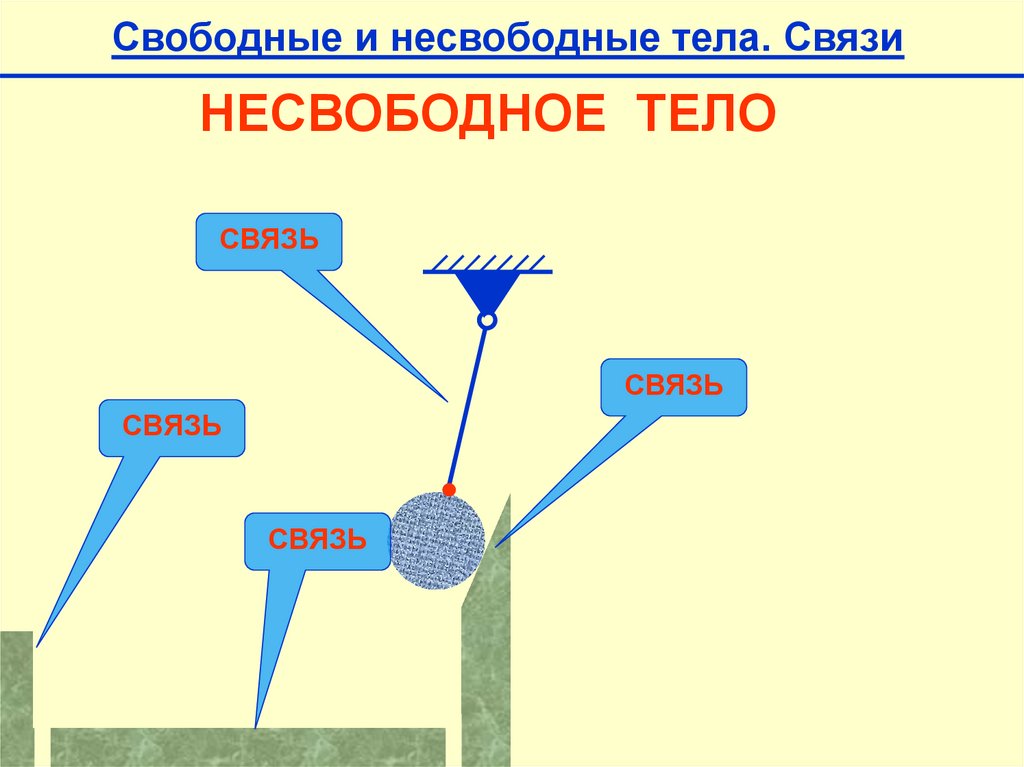
Свободные и несвободные тела. СвязиНЕСВОБОДНОЕ ТЕЛО
СВЯЗЬ
СВЯЗЬ
СВЯЗЬ
СВЯЗЬ
12.
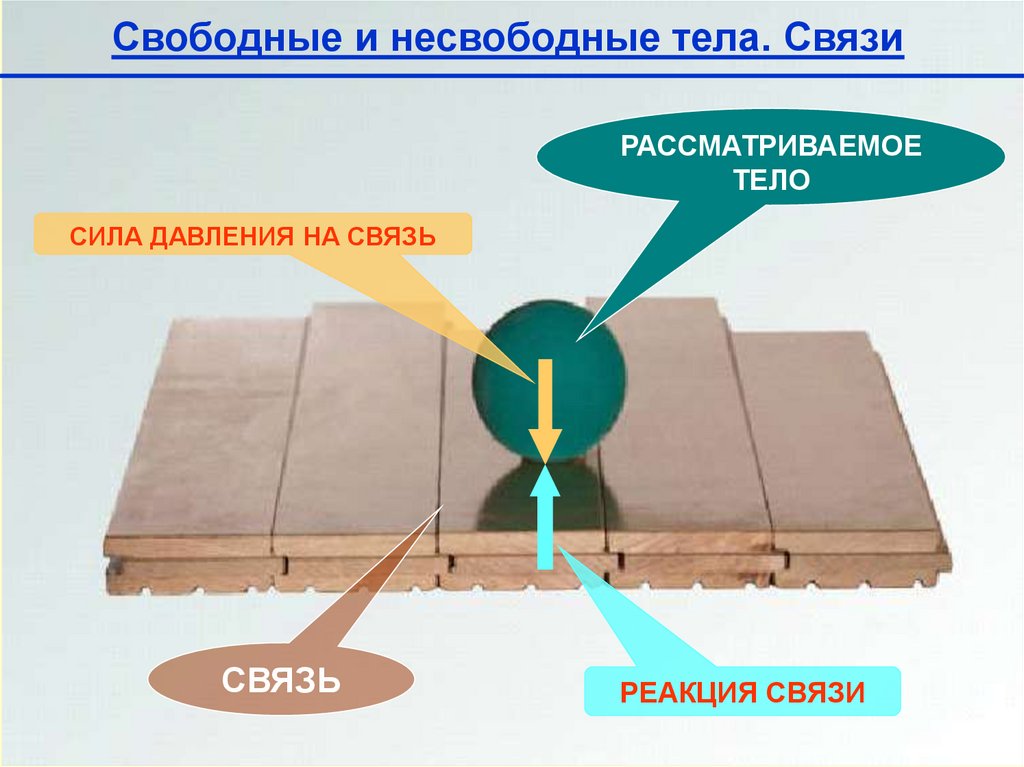
Свободные и несвободные тела. СвязиРАССМАТРИВАЕМОЕ
ТЕЛО
СИЛА ДАВЛЕНИЯ НА СВЯЗЬ
СВЯЗЬ
РЕАКЦИЯ СВЯЗИ
13.
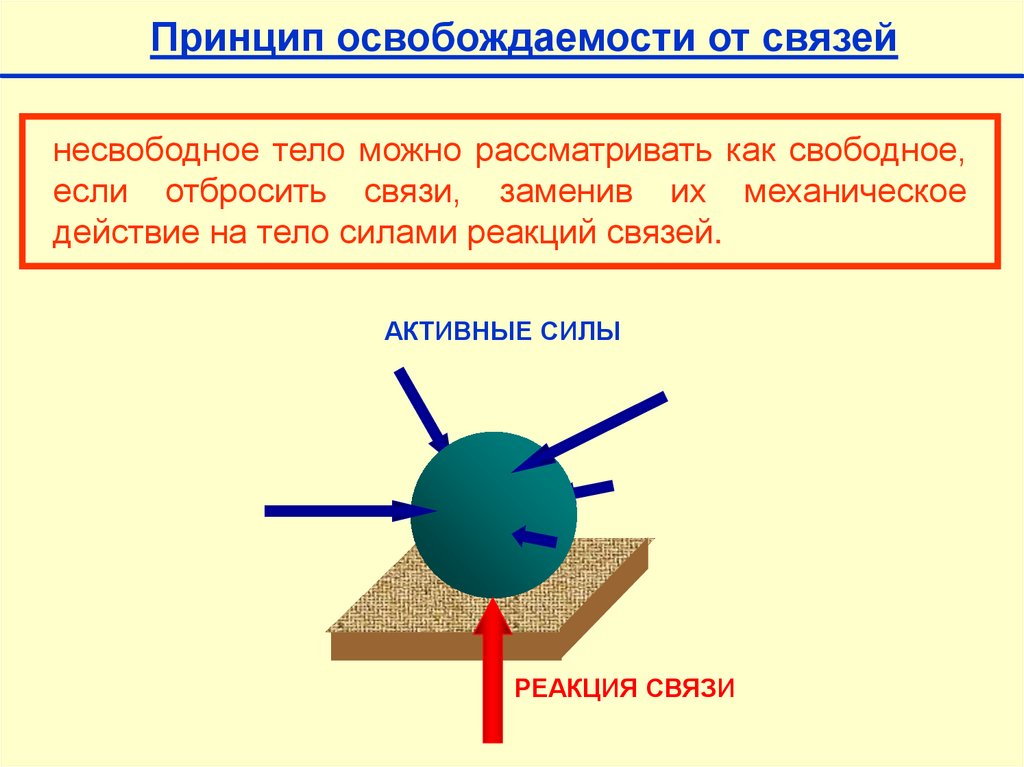
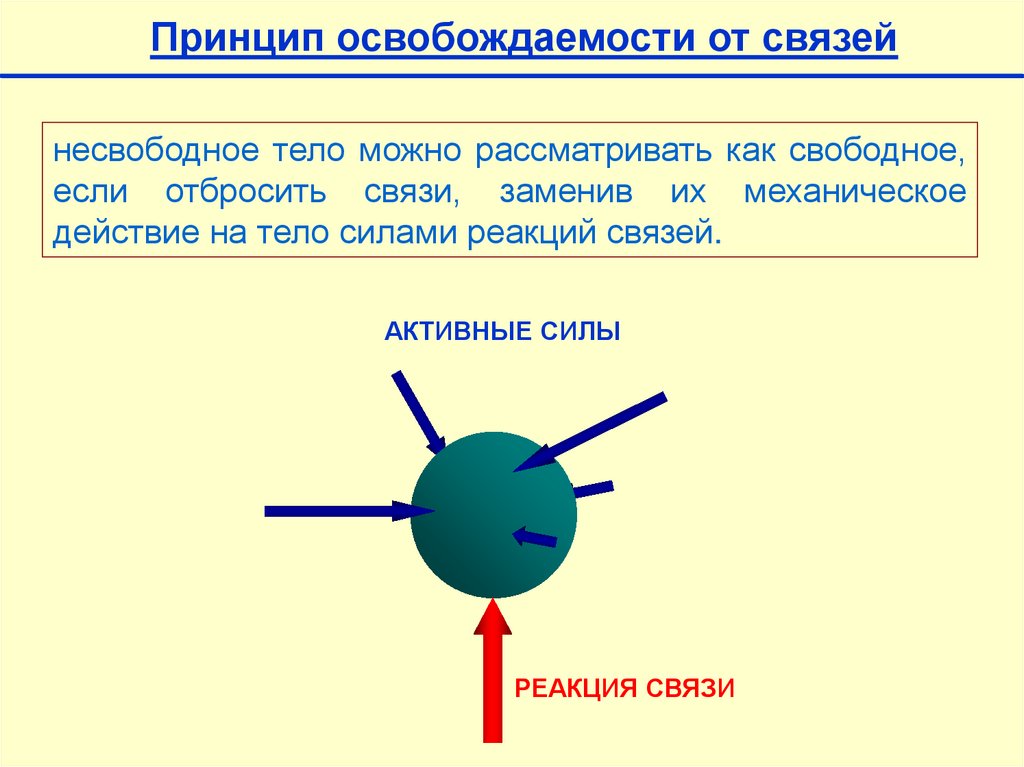
Принцип освобождаемости от связейнесвободное тело можно рассматривать как свободное,
если отбросить связи, заменив их механическое
действие на тело силами реакций связей.
АКТИВНЫЕ СИЛЫ
РЕАКЦИЯ СВЯЗИ
14.
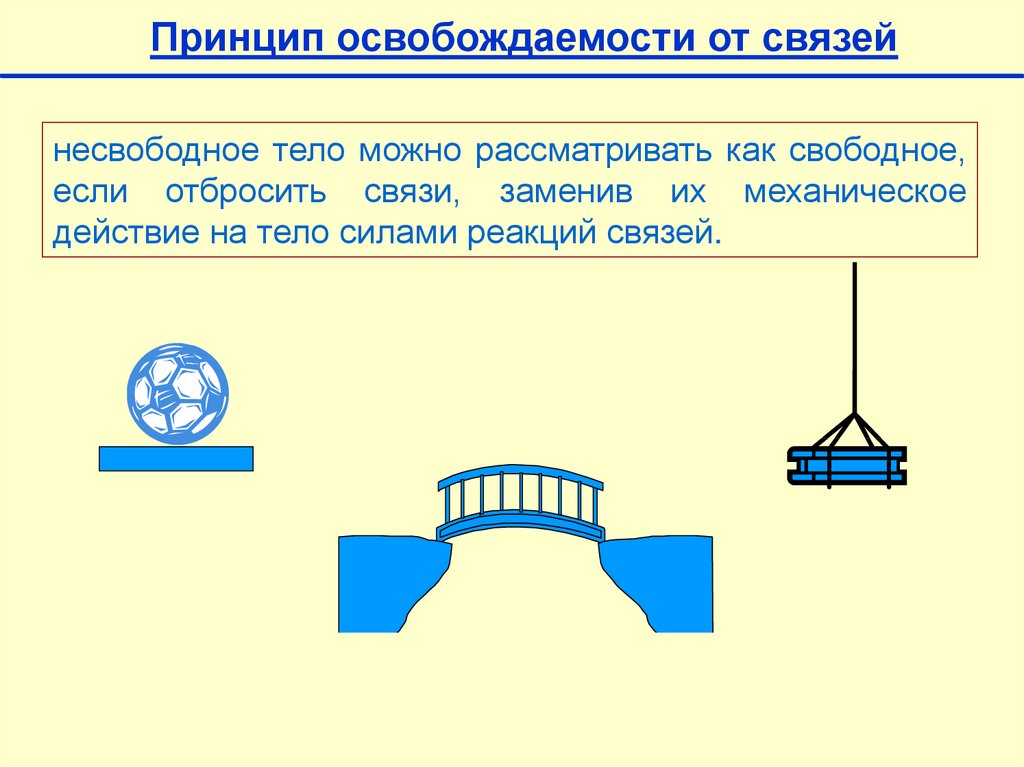
Принцип освобождаемости от связейнесвободное тело можно рассматривать как свободное,
если отбросить связи, заменив их механическое
действие на тело силами реакций связей.
АКТИВНЫЕ СИЛЫ
РЕАКЦИЯ СВЯЗИ
15.
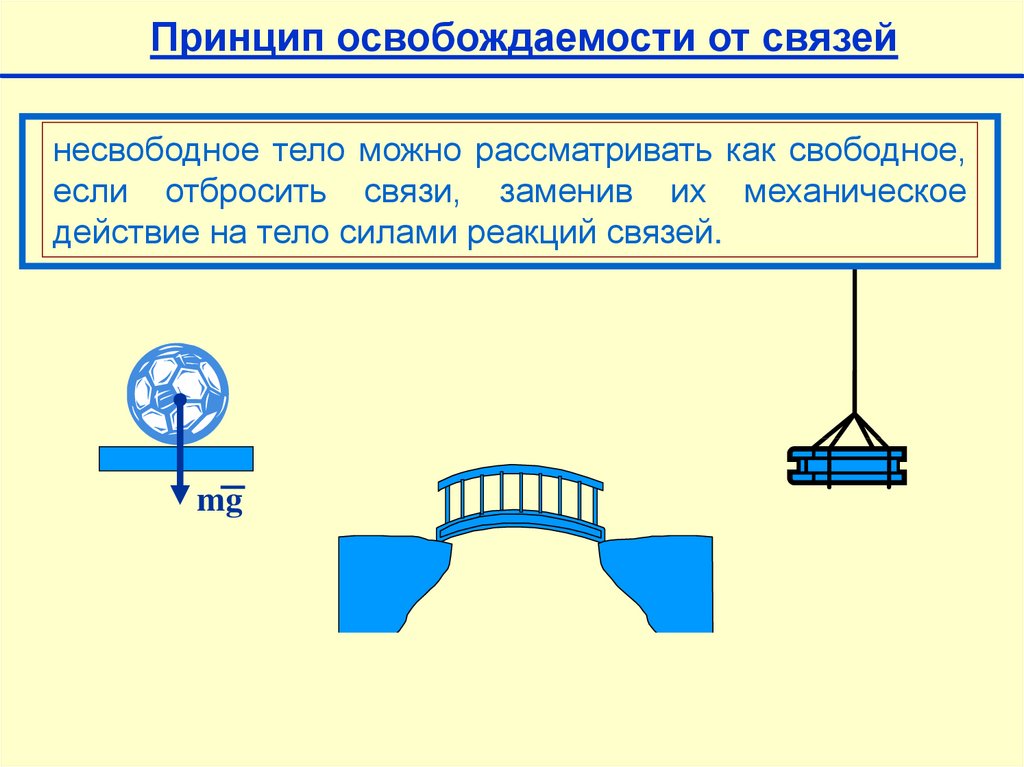
Принцип освобождаемости от связейнесвободное тело можно рассматривать как свободное,
если отбросить связи, заменив их механическое
действие на тело силами реакций связей.
16.
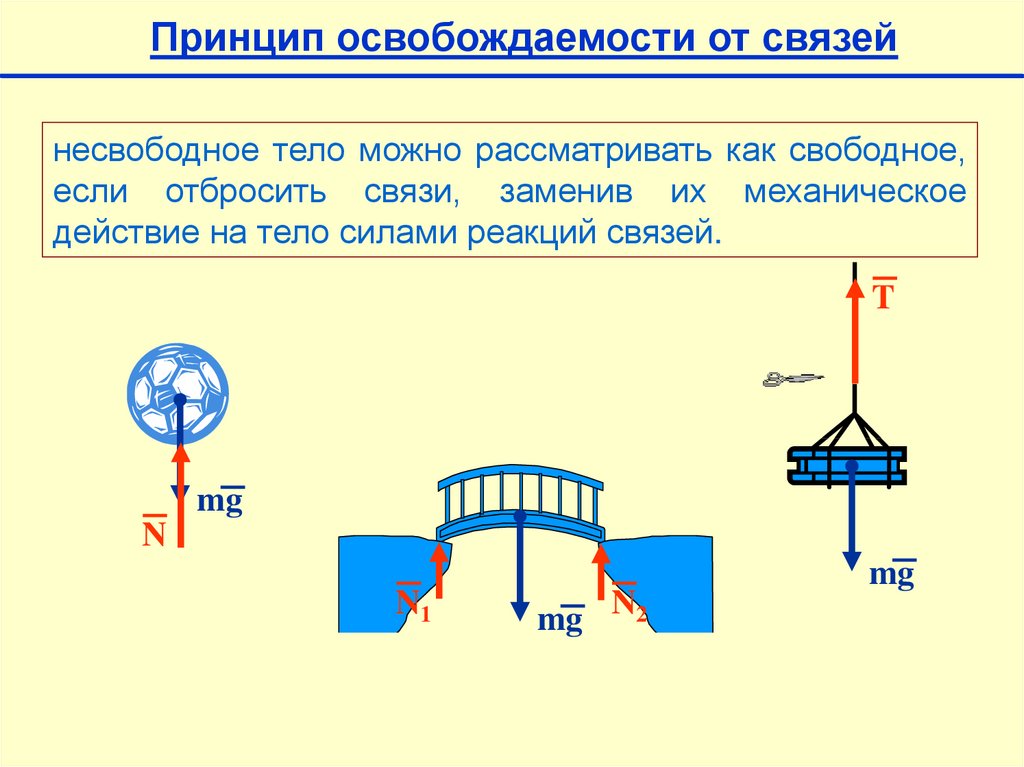
Принцип освобождаемости от связейнесвободное тело можно рассматривать как свободное,
если отбросить связи, заменив их механическое
действие на тело силами реакций связей.
mg
17.
Принцип освобождаемости от связейнесвободное тело можно рассматривать как свободное,
если отбросить связи, заменив их механическое
действие на тело силами реакций связей.
T
mg
N
N1
mg N2
mg
18.
2. Основные виды связейи их реакции
19.
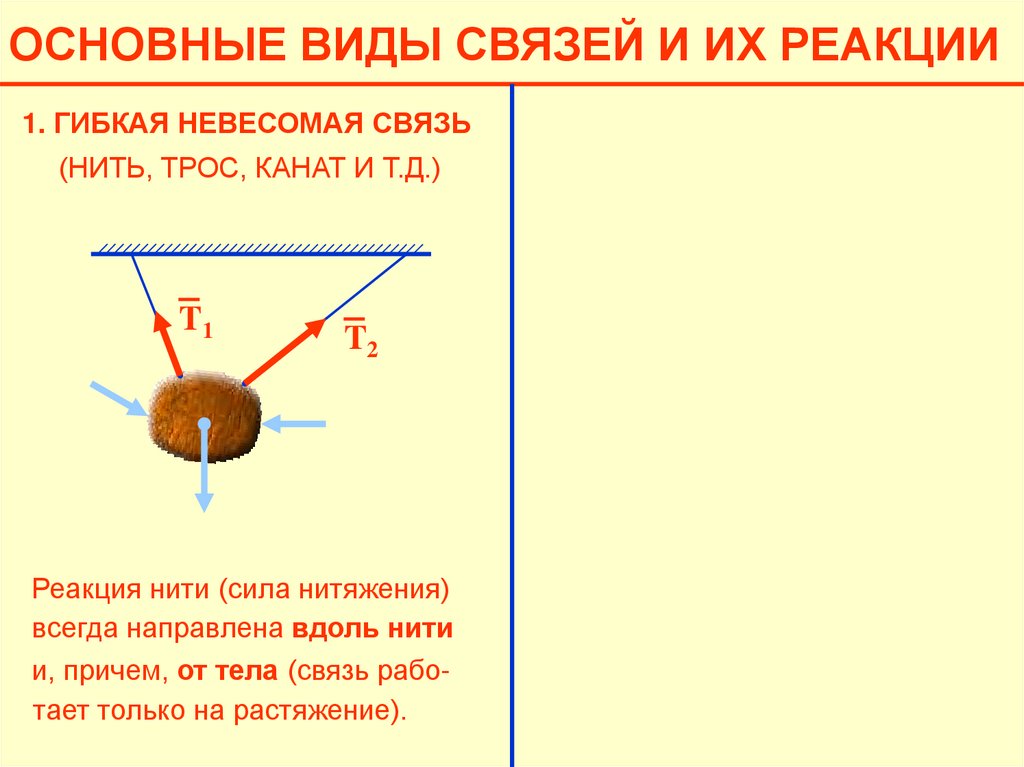
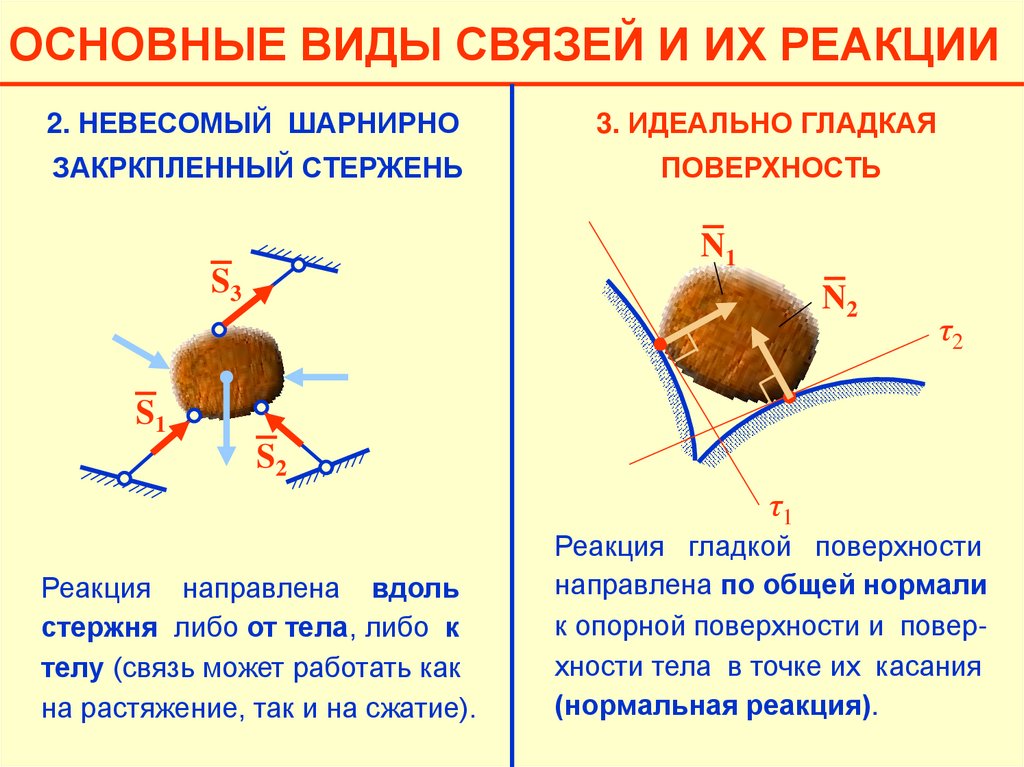
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ1. ГИБКАЯ НЕВЕСОМАЯ СВЯЗЬ
(НИТЬ, ТРОС, КАНАТ И Т.Д.)
T1
T2
Реакция нити (сила нитяжения)
всегда направлена вдоль нити
и, причем, от тела (связь работает только на растяжение).
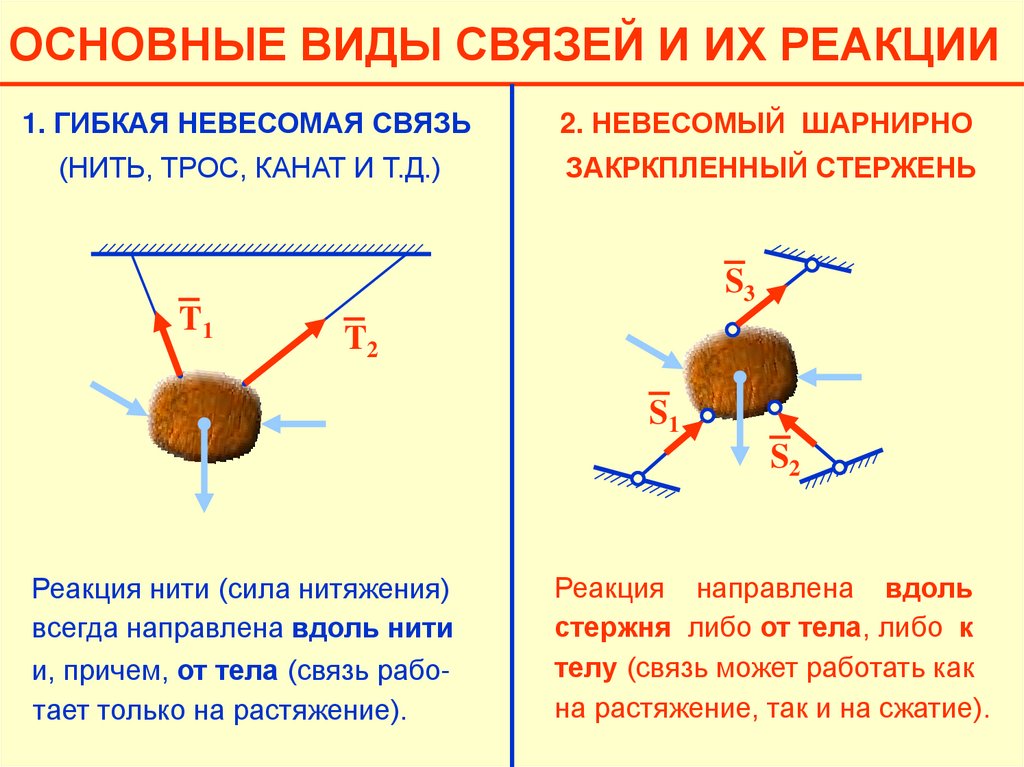
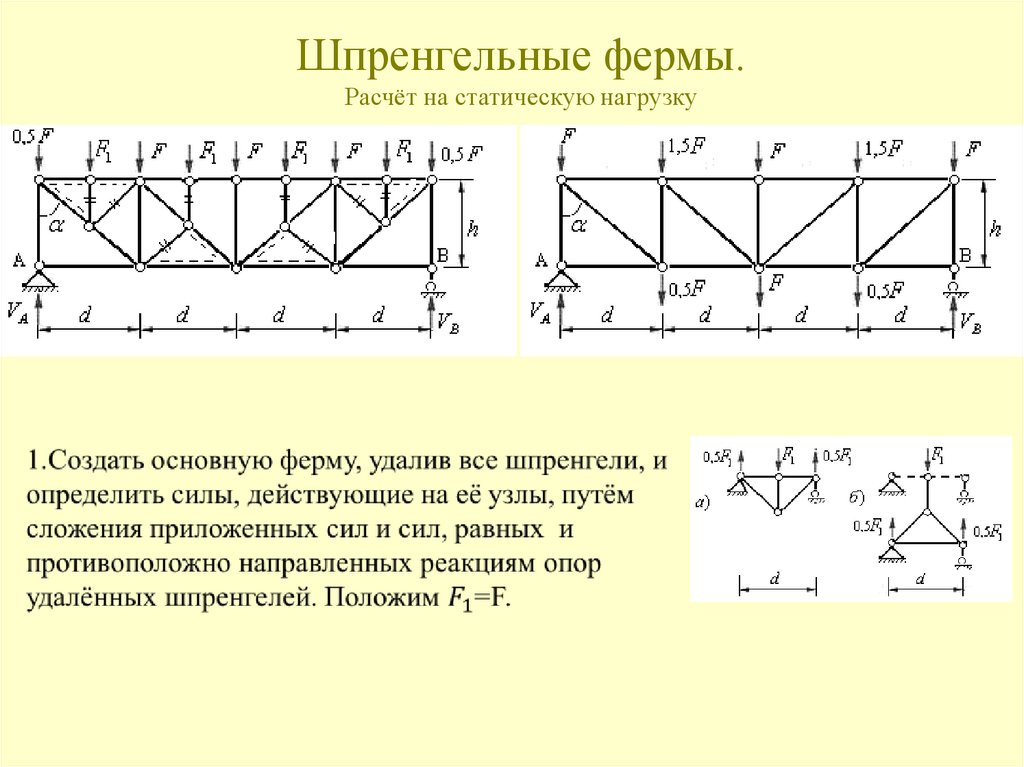
20.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ1. ГИБКАЯ НЕВЕСОМАЯ СВЯЗЬ
2. НЕВЕСОМЫЙ ШАРНИРНО
(НИТЬ, ТРОС, КАНАТ И Т.Д.)
ЗАКРКПЛЕННЫЙ СТЕРЖЕНЬ
S3
T1
T2
S1
S2
Реакция нити (сила нитяжения)
всегда направлена вдоль нити
и, причем, от тела (связь работает только на растяжение).
Реакция направлена вдоль
стержня либо от тела, либо к
телу (связь может работать как
на растяжение, так и на сжатие).
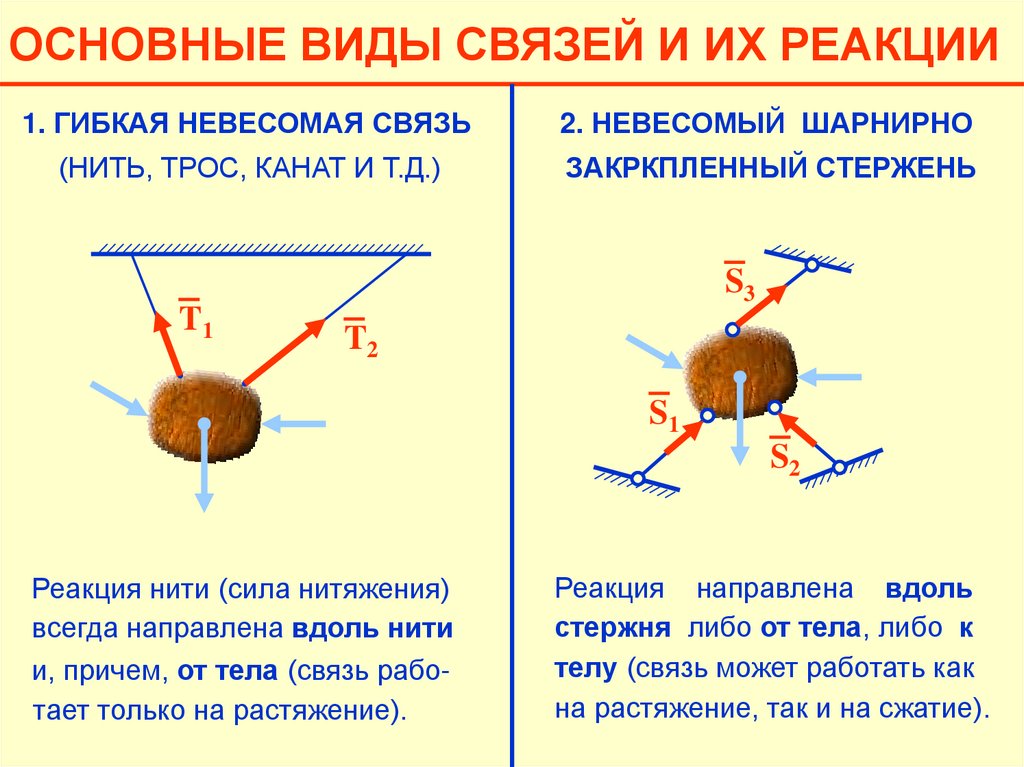
21.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ1. ГИБКАЯ НЕВЕСОМАЯ СВЯЗЬ
2. НЕВЕСОМЫЙ ШАРНИРНО
(НИТЬ, ТРОС, КАНАТ И Т.Д.)
ЗАКРКПЛЕННЫЙ СТЕРЖЕНЬ
S3
T1
T2
S1
S2
Реакция нити (сила нитяжения)
всегда направлена вдоль нити
и, причем, от тела (связь работает только на растяжение).
Реакция направлена вдоль
стержня либо от тела, либо к
телу (связь может работать как
на растяжение, так и на сжатие).
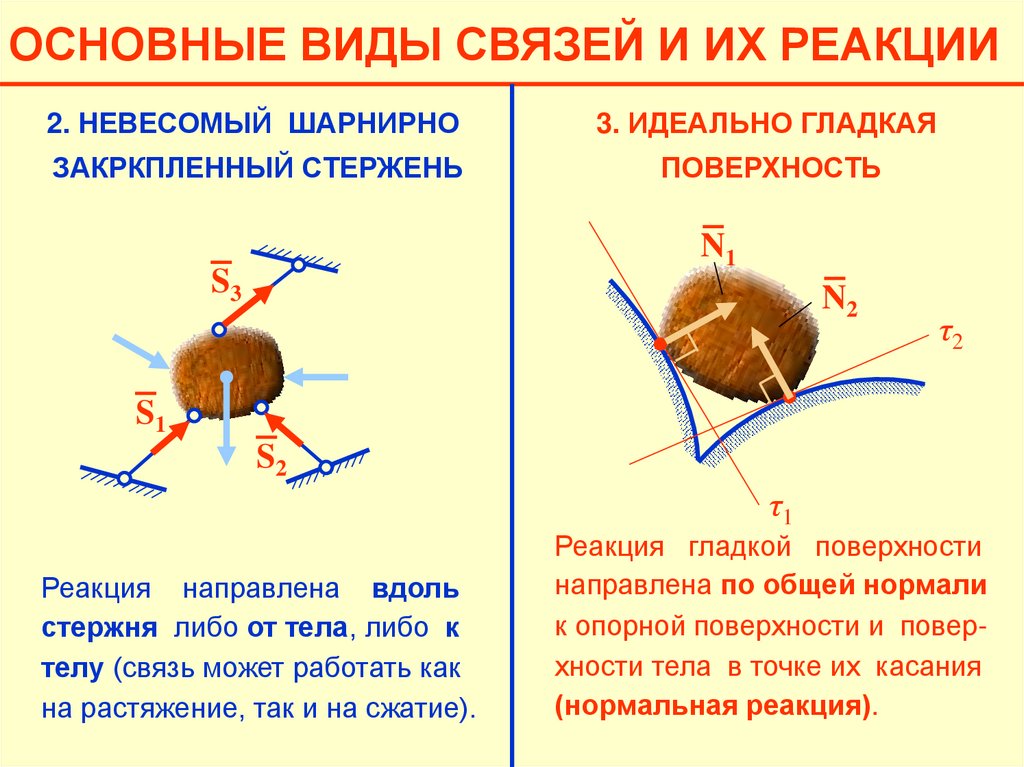
22.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ2. НЕВЕСОМЫЙ ШАРНИРНО
3. ИДЕАЛЬНО ГЛАДКАЯ
ЗАКРКПЛЕННЫЙ СТЕРЖЕНЬ
ПОВЕРХНОСТЬ
N1
S3
N2
τ2
S1
S2
τ1
Реакция направлена вдоль
стержня либо от тела, либо к
телу (связь может работать как
на растяжение, так и на сжатие).
Реакция гладкой поверхности
направлена по общей нормали
к опорной поверхности и поверхности тела в точке их касания
(нормальная реакция).
23.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ2. НЕВЕСОМЫЙ ШАРНИРНО
3. ИДЕАЛЬНО ГЛАДКАЯ
ЗАКРКПЛЕННЫЙ СТЕРЖЕНЬ
ПОВЕРХНОСТЬ
N1
S3
N2
τ2
S1
S2
τ1
Реакция направлена вдоль
стержня либо от тела, либо к
телу (связь может работать как
на растяжение, так и на сжатие).
Реакция гладкой поверхности
направлена по общей нормали
к опорной поверхности и поверхности тела в точке их касания
(нормальная реакция).
24.
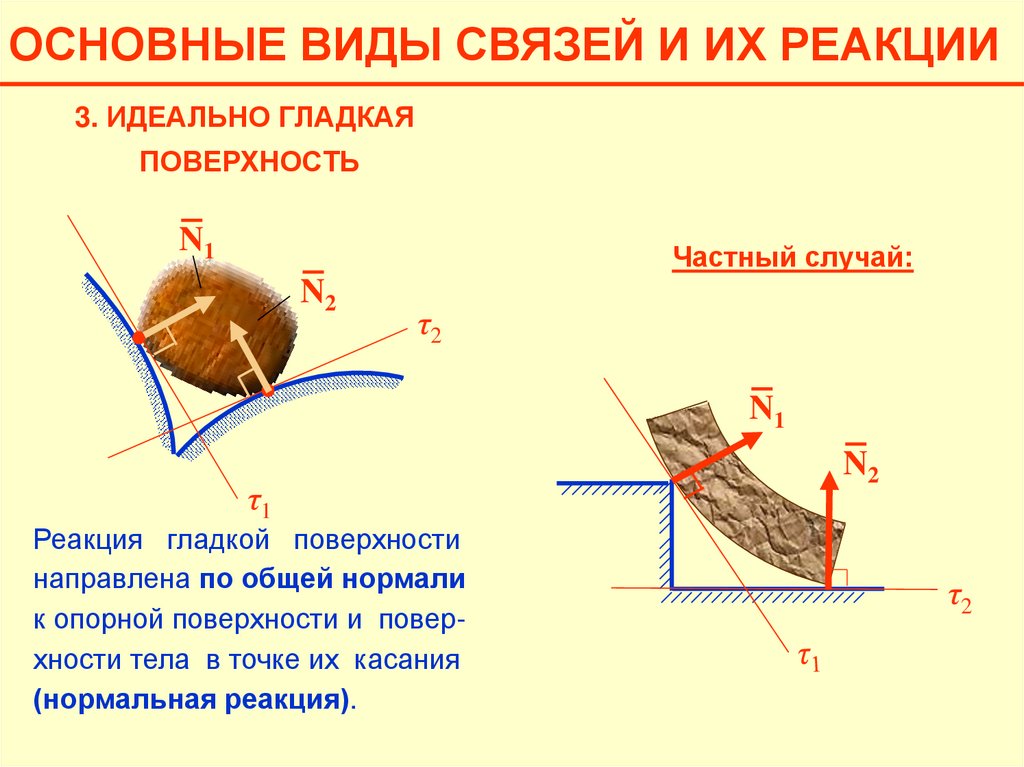
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ3. ИДЕАЛЬНО ГЛАДКАЯ
ПОВЕРХНОСТЬ
N1
Частный случай:
N2
τ2
N1
τ1
Реакция гладкой поверхности
направлена по общей нормали
к опорной поверхности и поверхности тела в точке их касания
(нормальная реакция).
N2
τ2
25.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ3. ИДЕАЛЬНО ГЛАДКАЯ
ПОВЕРХНОСТЬ
N1
Частный случай:
N2
τ2
N1
τ1
Реакция гладкой поверхности
направлена по общей нормали
к опорной поверхности и поверхности тела в точке их касания
(нормальная реакция).
N2
τ2
26.
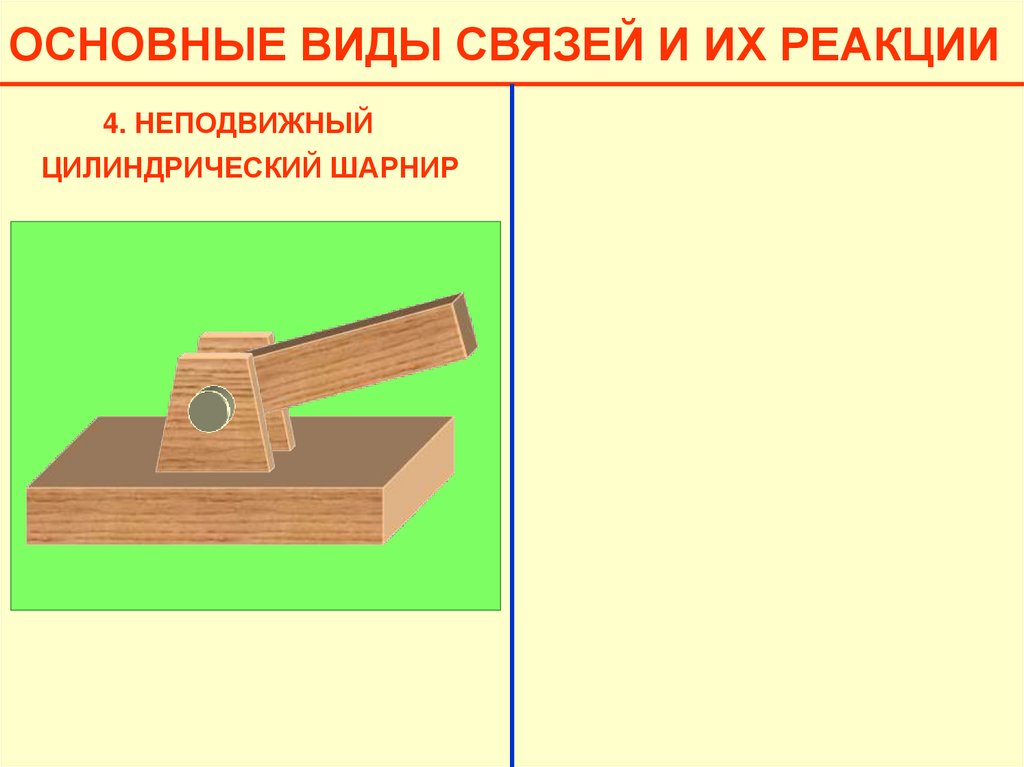
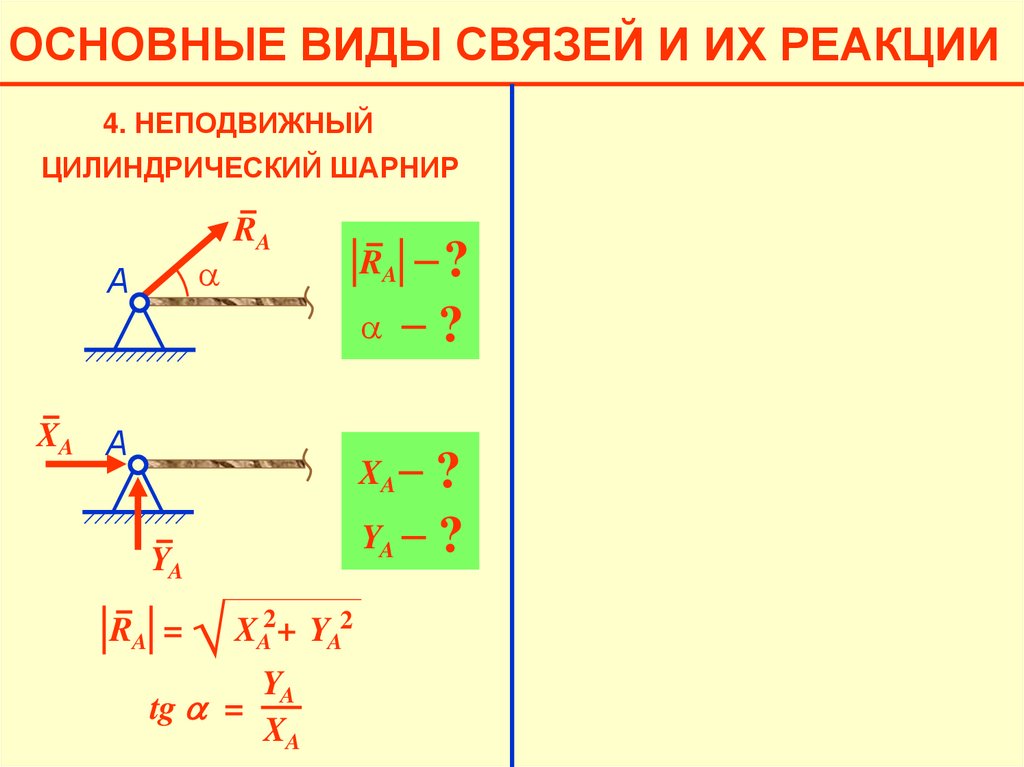
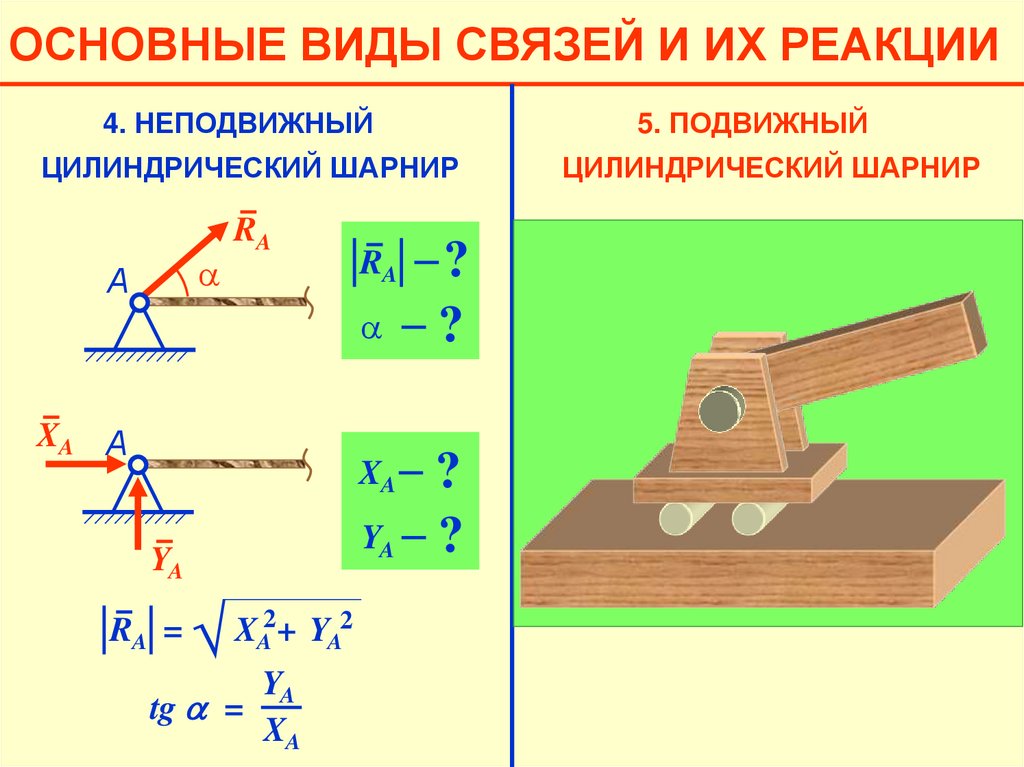
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
27.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
28.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
29.
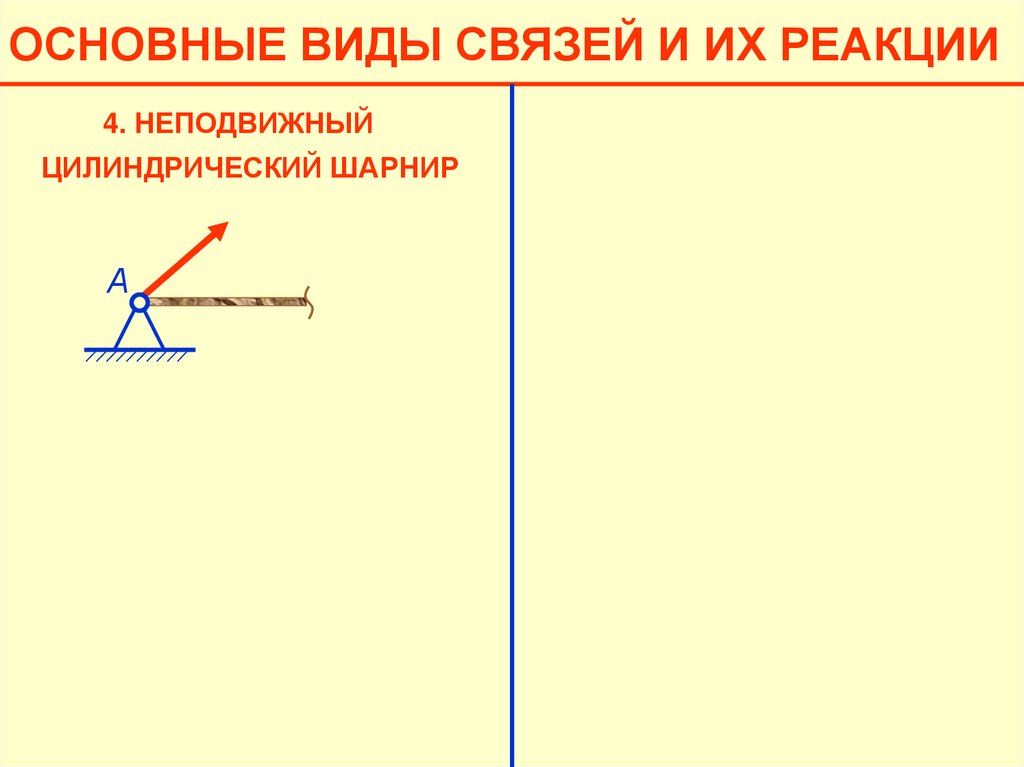
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
А
30.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
А
31.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
А
32.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
А
33.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
А
34.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
А
35.
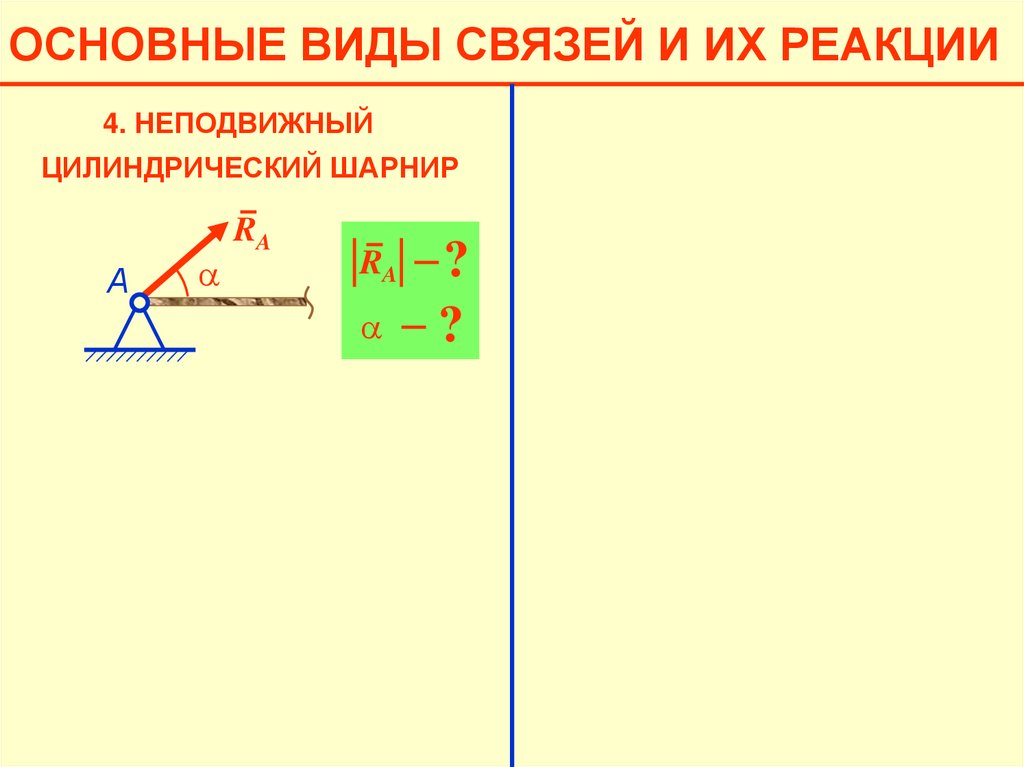
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
А
a
RA
RA
a
?
?
36.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
А
a
RA
RA
a
?
?
37.
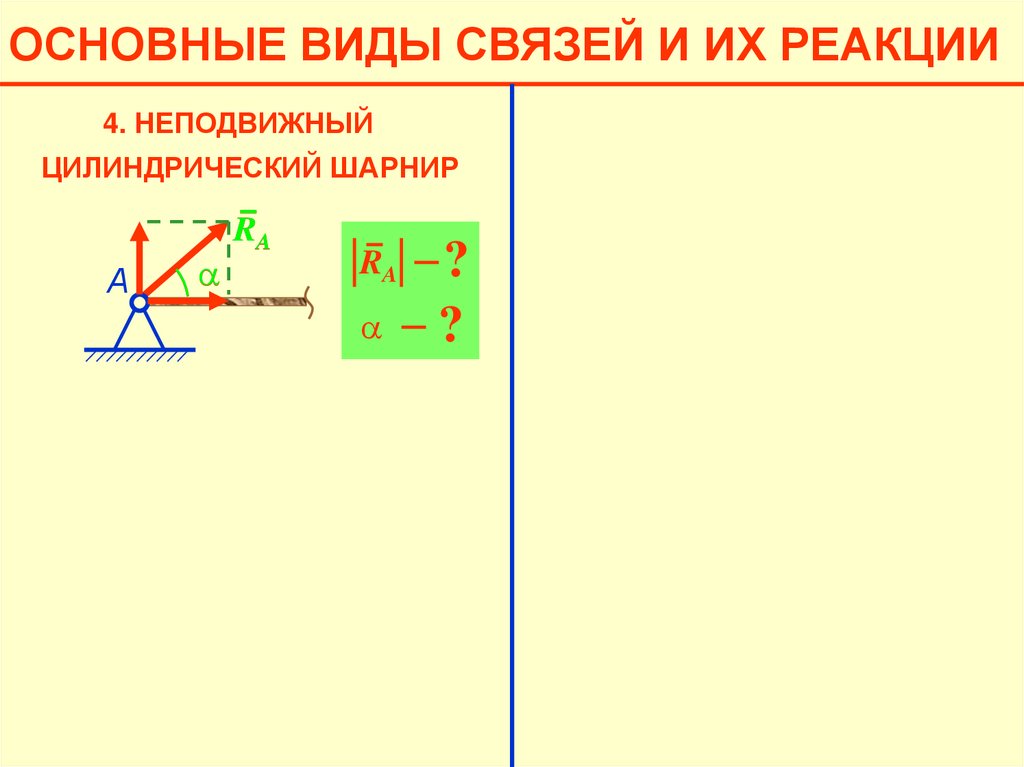
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
a
А
RA
RA
a
XA А
XA
YA
YA
?
?
?
?
38.
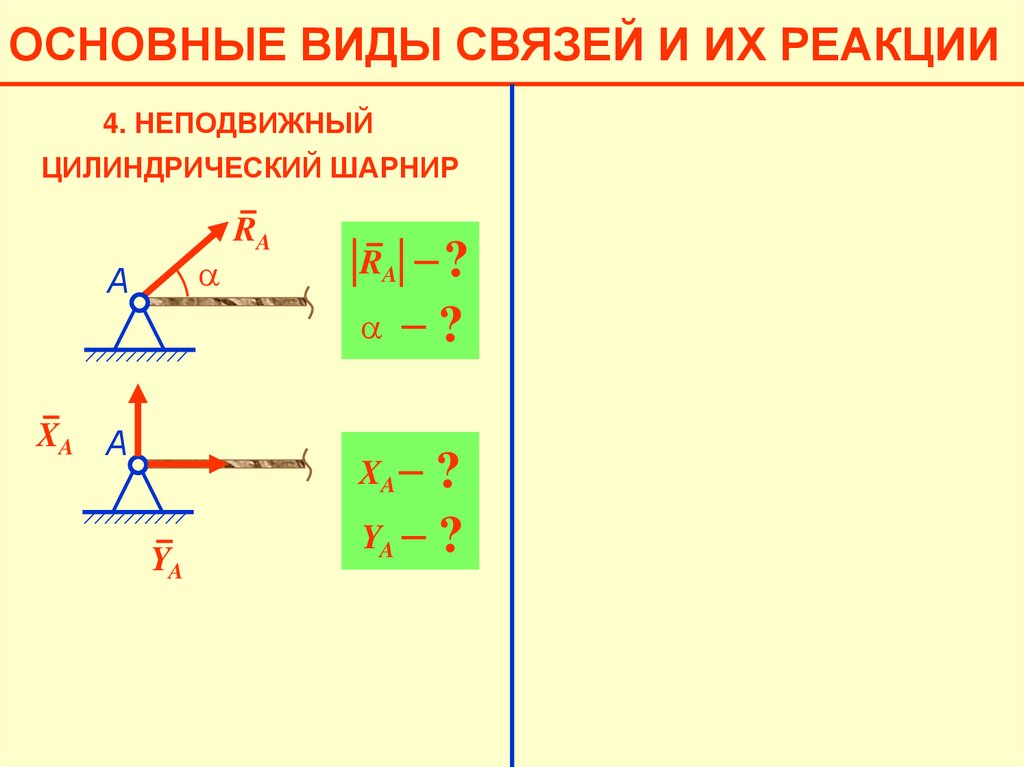
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
a
А
RA
RA
a
XA А
XA
YA
YA
RA =
√
XA2+ YA2
YA
tg a =
XA
?
?
?
?
39.
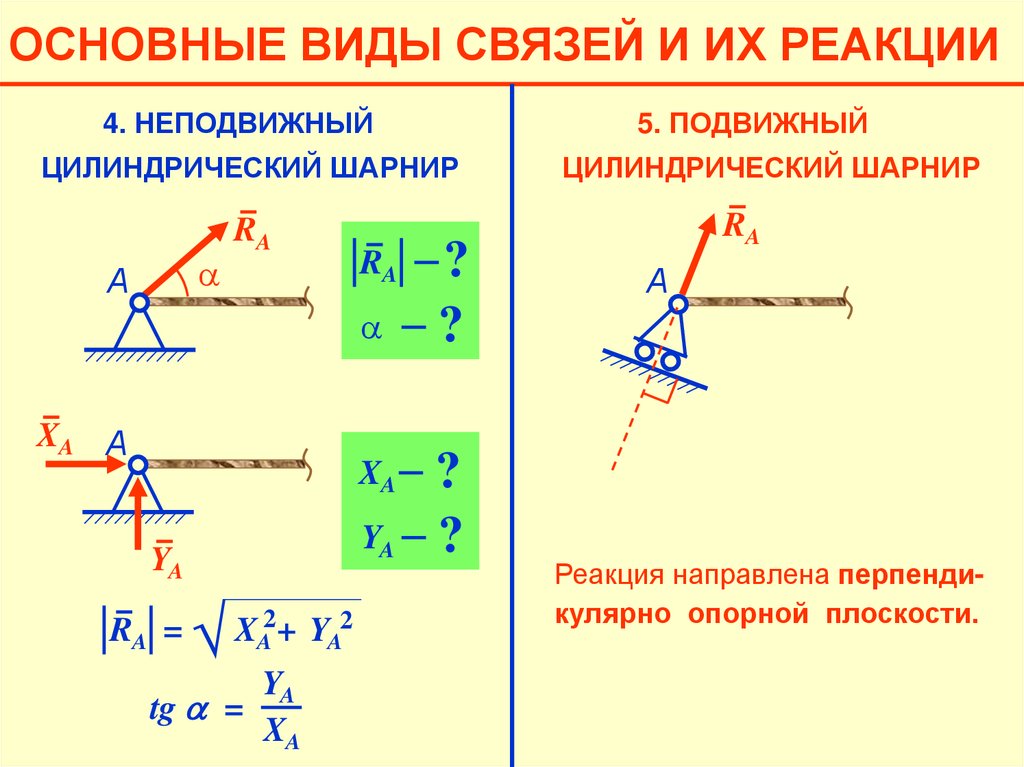
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
5. ПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
a
А
RA
RA
a
XA А
XA
YA
YA
RA =
√
XA2+ YA2
YA
tg a =
XA
?
?
?
?
40.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
5. ПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
a
А
RA
RA
a
XA А
XA
YA
YA
RA =
√
XA2+ YA2
YA
tg a =
XA
?
?
?
?
41.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
5. ПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
a
А
RA
RA
a
XA А
XA
YA
YA
RA =
√
XA2+ YA2
YA
tg a =
XA
?
?
?
?
42.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
5. ПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
a
А
RA
RA
a
XA А
XA
YA
YA
RA =
√
XA2+ YA2
YA
tg a =
XA
?
?
?
?
43.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ4. НЕПОДВИЖНЫЙ
5. ПОДВИЖНЫЙ
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
ЦИЛИНДРИЧЕСКИЙ ШАРНИР
a
А
RA
RA
a
XA А
XA
YA
YA
RA =
√
XA2+ YA2
YA
tg a =
XA
?
?
?
?
RA
А
Реакция направлена перпендикулярно опорной плоскости.
44.
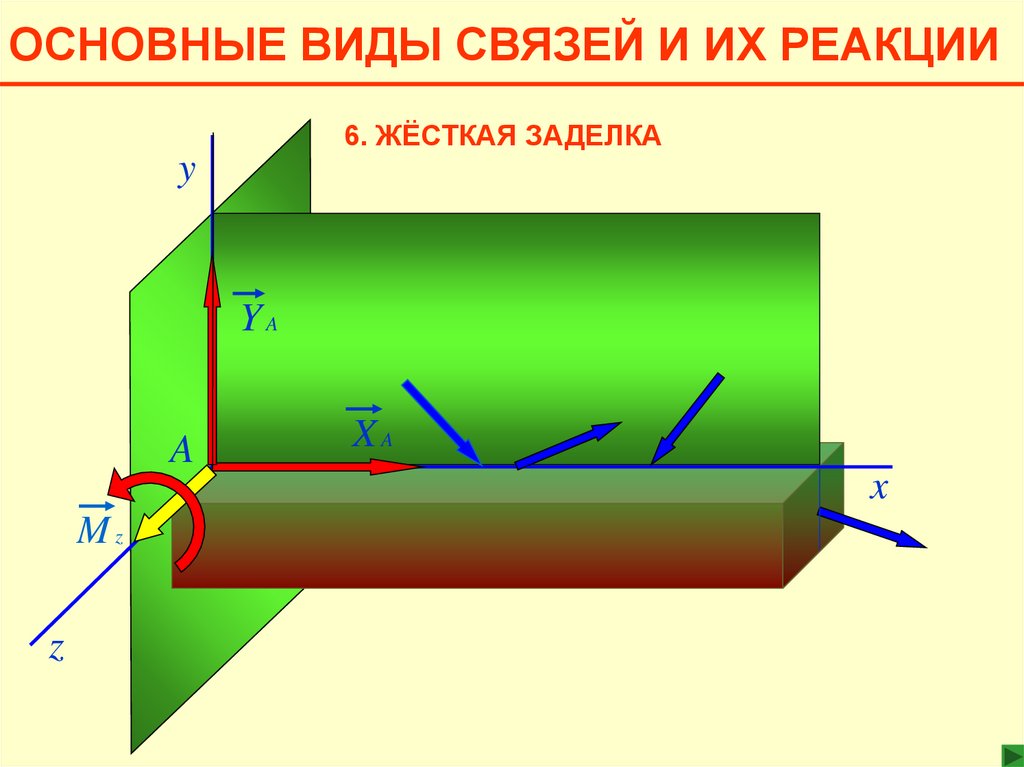
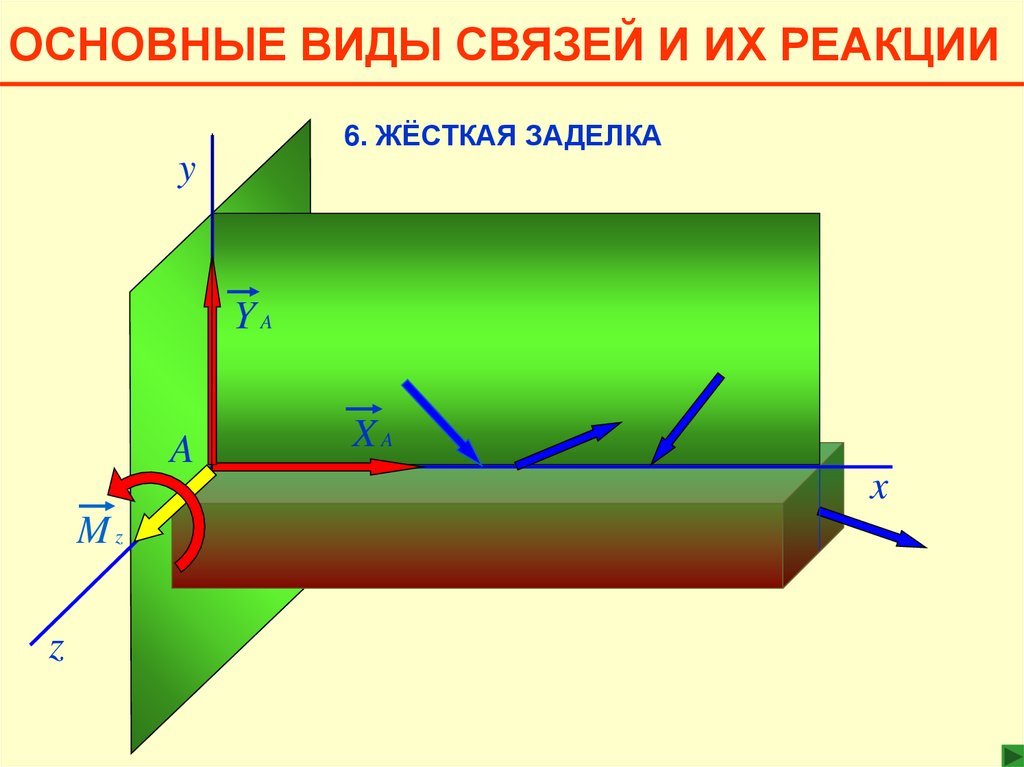
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ6. ЖЁСТКАЯ ЗАДЕЛКА
y
YA
A
XA
x
Mz
z
45.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ6. ЖЁСТКАЯ ЗАДЕЛКА
y
YA
A
XA
x
Mz
z
46.
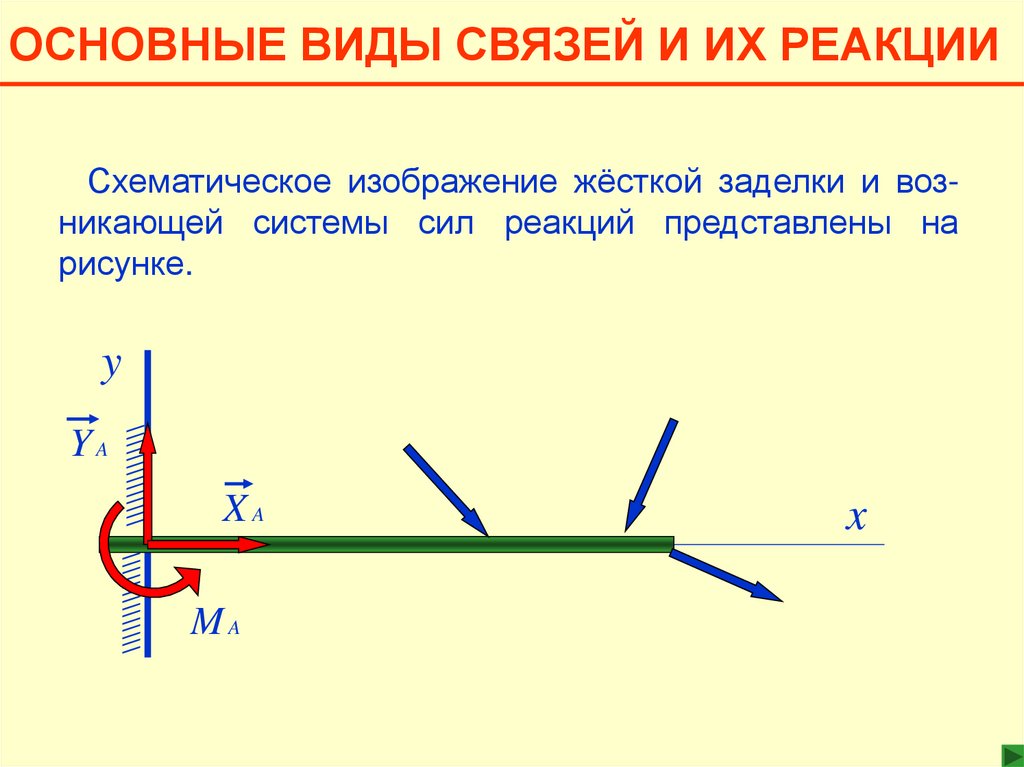
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ6. ЖЁСТКАЯ ЗАДЕЛКА
Схематическое изображение жёсткой заделки и возникающей системы сил реакций представлены на
рисунке.
y
\\\\\\\\\\\\\\
XA
YA
\\\\\\\\\\\\\\
MA
x
47.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИСхематическое изображение жёсткой заделки и возникающей системы сил реакций представлены на
рисунке.
y
\\\\\\\\\\\\\\
YA
XA
\\\\\\\\\\\\\\
MA
x
48.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИy
о
x
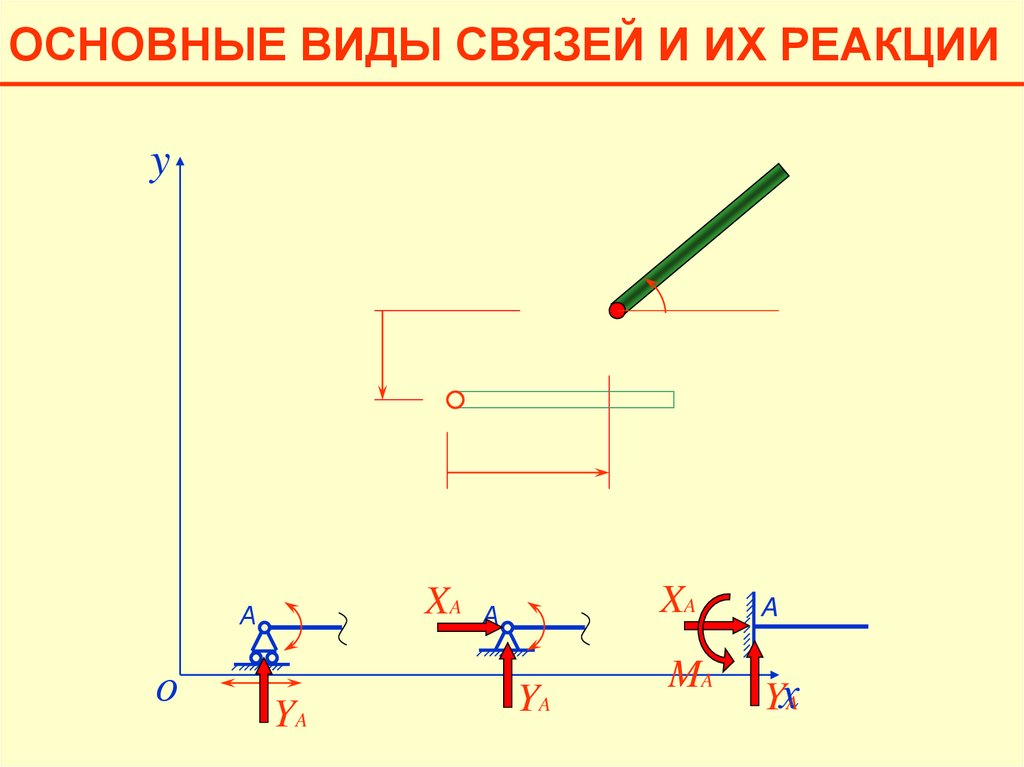
49.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИy
о
x
50.
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИy
о
XA
XA А
А
YA
YA
MA
A
YxA
51.
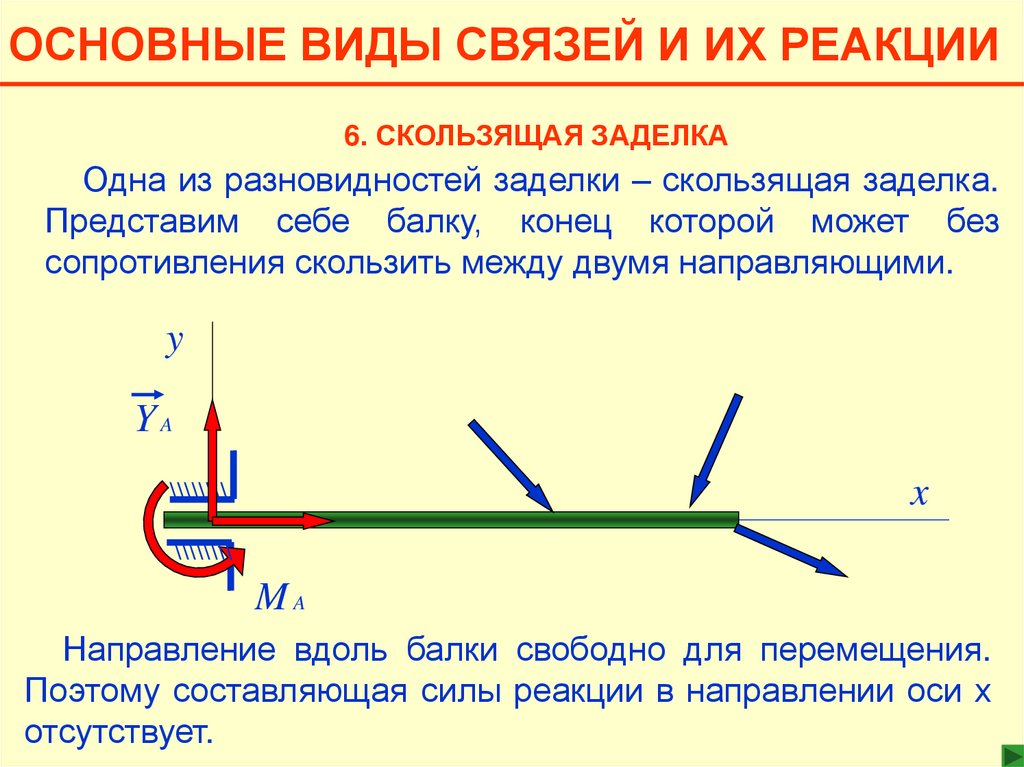
ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ6. СКОЛЬЗЯЩАЯ ЗАДЕЛКА
Одна из разновидностей заделки – скользящая заделка.
Представим себе балку, конец которой может без
сопротивления скользить между двумя направляющими.
y
YA
x
\\\\\\\\
\\\\\\\\
MA
Направление вдоль балки свободно для перемещения.
Поэтому составляющая силы реакции в направлении оси х
отсутствует.
52.
3. Виды нагрузки53.
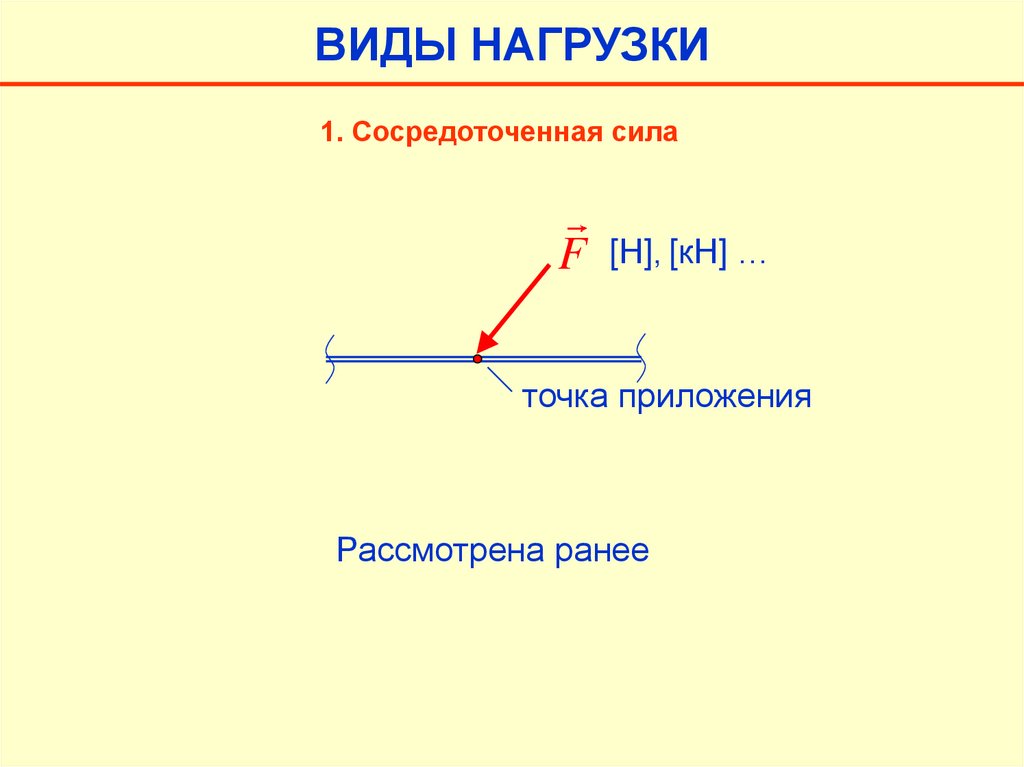
ВИДЫ НАГРУЗКИ1. Сосредоточенная сила
F [Н], [кН] …
точка приложения
Рассмотрена ранее
54.
ВИДЫ НАГРУЗКИ2. Распределенная нагрузка
Помимо
сосредоточенных
сил,
приложенных
в
определенных точках тела, на практике часто приходится
иметь дело с нагрузками, распределенными в соответствии с
некоторым законом по какому-либо объему, поверхности или
линии (сила тяжести, действующая на каждую частицу тела,
сила давления ветра, гидростатическое давление и т. д.).
Величина силы, приходящаяся на единицу объема, площади
или длины тела, называется интенсивностью нагрузки и
имеет размерность , или , соответственно Н/м3, Н/м2, Н/м.
q(x)
С
D
A
xн
q(x) – интенсивность [Н/м]
В
xк
x
55.
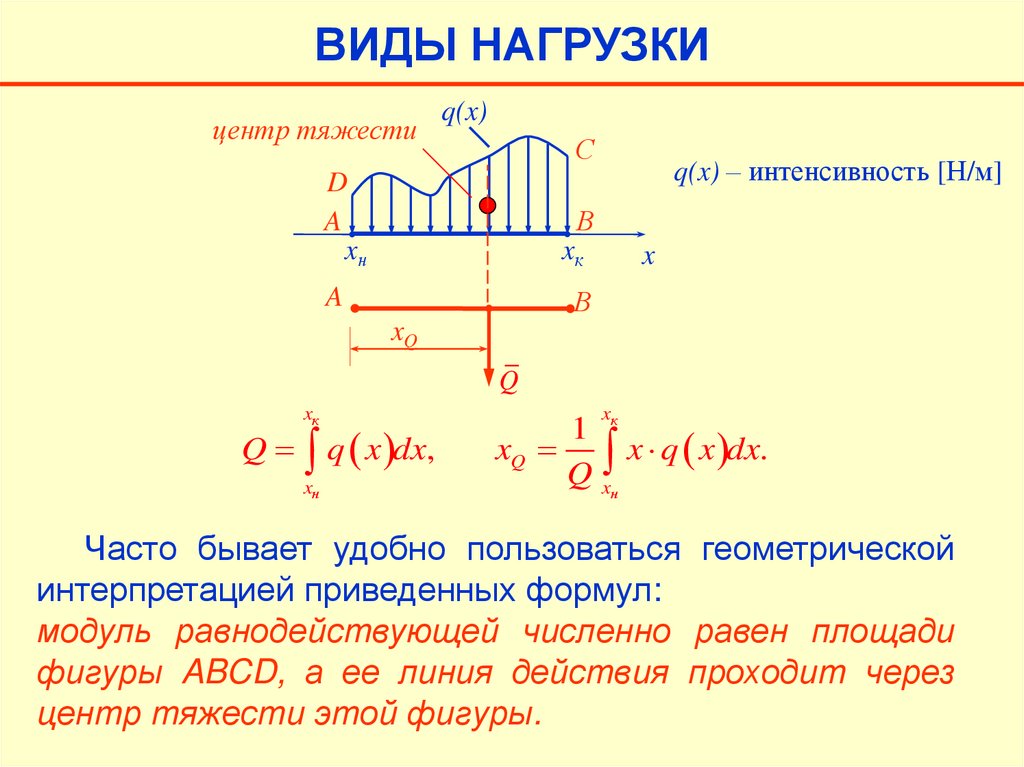
ВИДЫ НАГРУЗКИq(x)
С
D
A
xн
xк
A
В
q(x) – интенсивность [Н/м]
В
x
xQ
Q
При решении задач на определение реакций связей
распределенная
нагрузка
заменяется
одной
силой
–
равнодействующей.
Величина Q равнодействующей и координата xQ ее точки
приложения могут быть вычислены по формулам:
xк
Q q x dx,
xн
x
1 к
xQ x q x dx.
Q xн
56.
ВИДЫ НАГРУЗКИцентр тяжести
q(x)
С
D
A
xн
xк
A
В
q(x) – интенсивность [Н/м]
В
x
xQ
Q
xк
Q q x dx,
xн
xQ
xк
1
x q x dx.
Q xн
Часто бывает удобно пользоваться геометрической
интерпретацией приведенных формул:
модуль равнодействующей численно равен площади
фигуры ABCD, а ее линия действия проходит через
центр тяжести этой фигуры.
57.
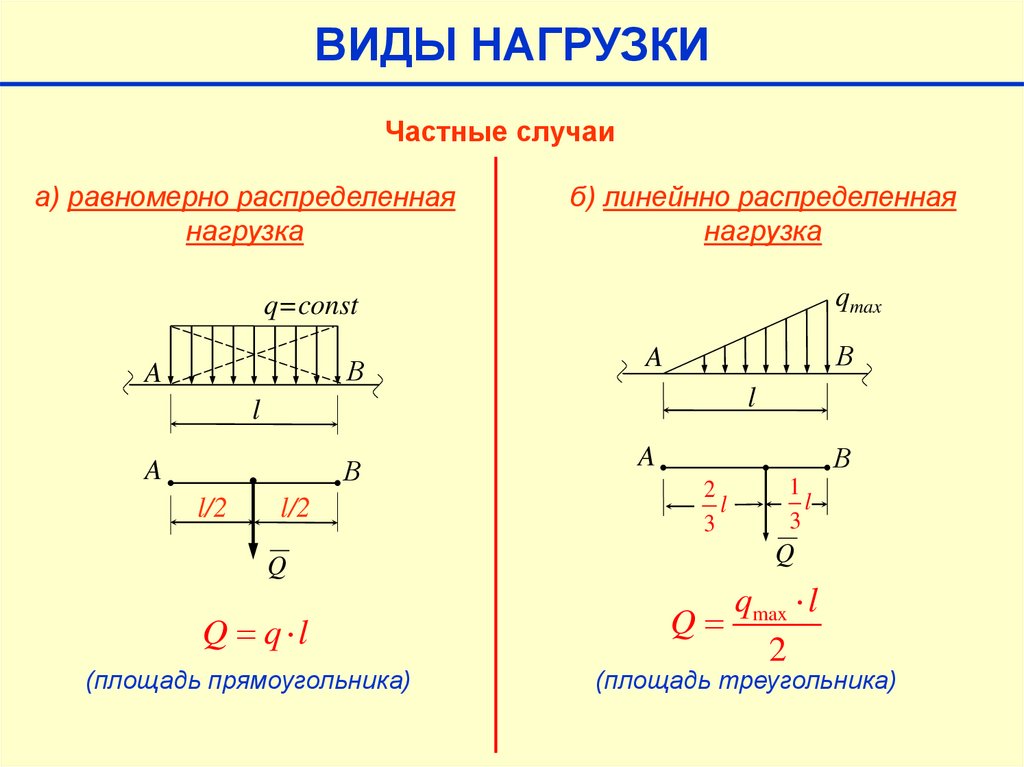
ВИДЫ НАГРУЗКИЧастные случаи
а) равномерно распределенная
нагрузка
б) линейнно распределенная
нагрузка
qmax
q=const
В
A
В
A
l
l
В
A
l/2
l/2
Q
Q q l
(площадь прямоугольника)
В
A
2
l
3
1
l
3
Q
qmax l
Q
2
(площадь треугольника)
58.
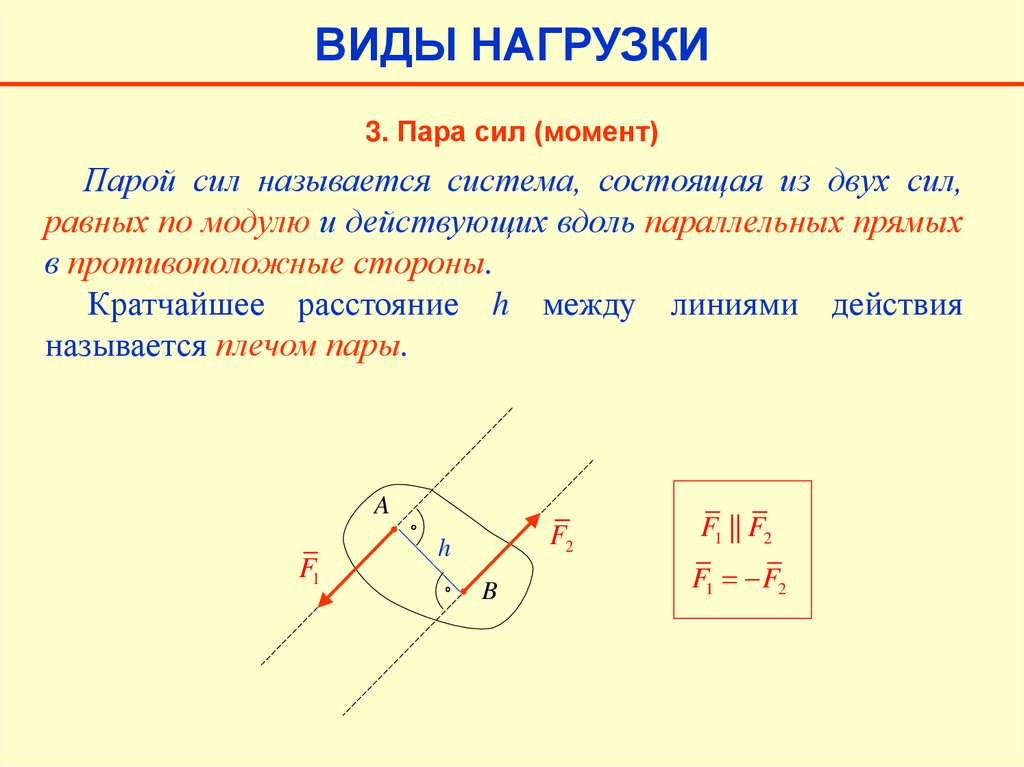
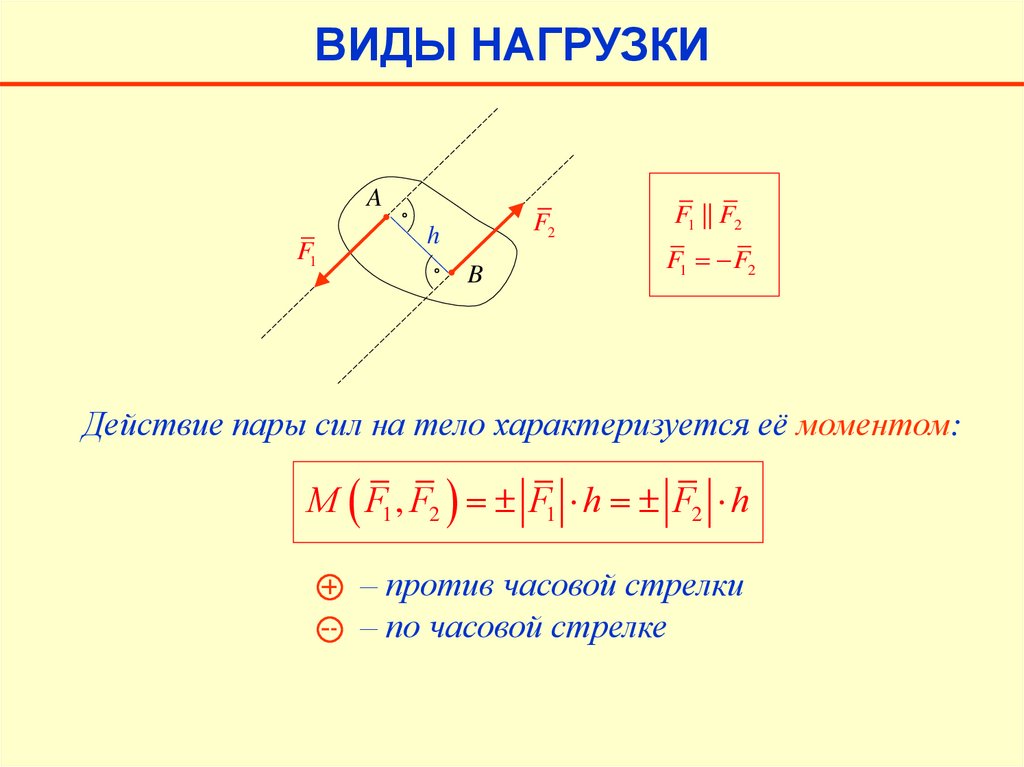
ВИДЫ НАГРУЗКИ3. Пара сил (момент)
Парой сил называется система, состоящая из двух сил,
равных по модулю и действующих вдоль параллельных прямых
в противоположные стороны.
Кратчайшее расстояние h между линиями действия
называется плечом пары.
A
F1
F2
h
B
F1 || F2
F1 F2
59.
ВИДЫ НАГРУЗКИA
F1
F2
h
B
F1 || F2
F1 F2
Действие пары сил на тело характеризуется её моментом:
М F1 , F2 F1 h F2 h
– против часовой стрелки
– по часовой стрелке
60.
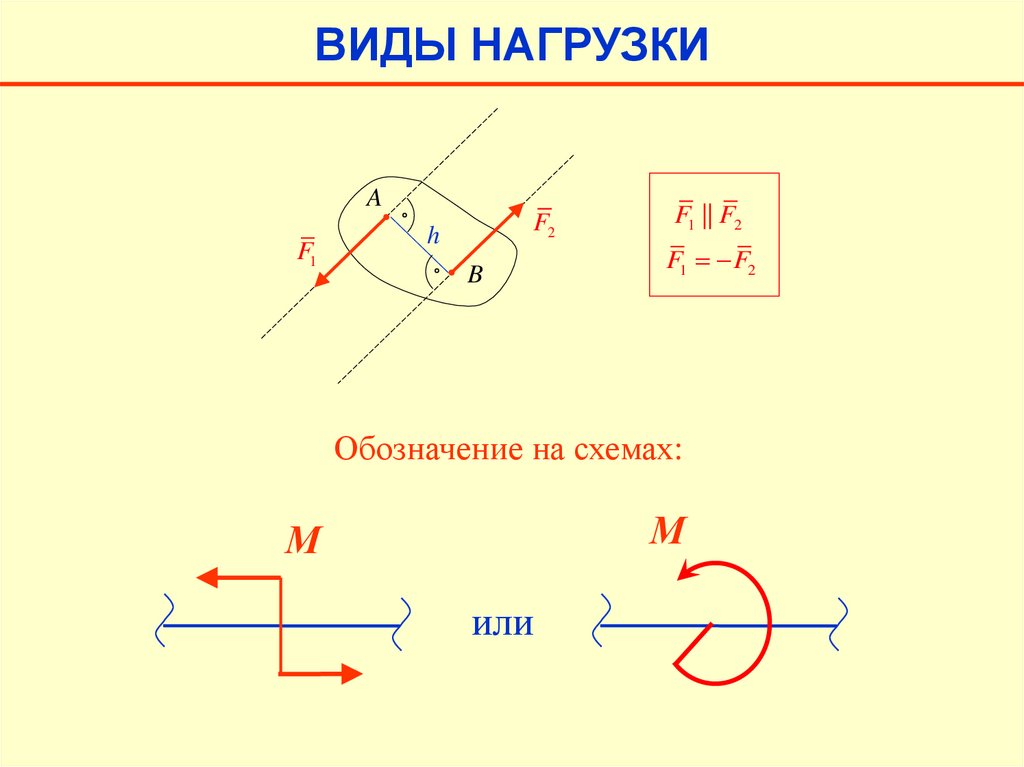
ВИДЫ НАГРУЗКИA
F1
F2
h
B
F1 || F2
F1 F2
Обозначение на схемах:
М
М
или
61.
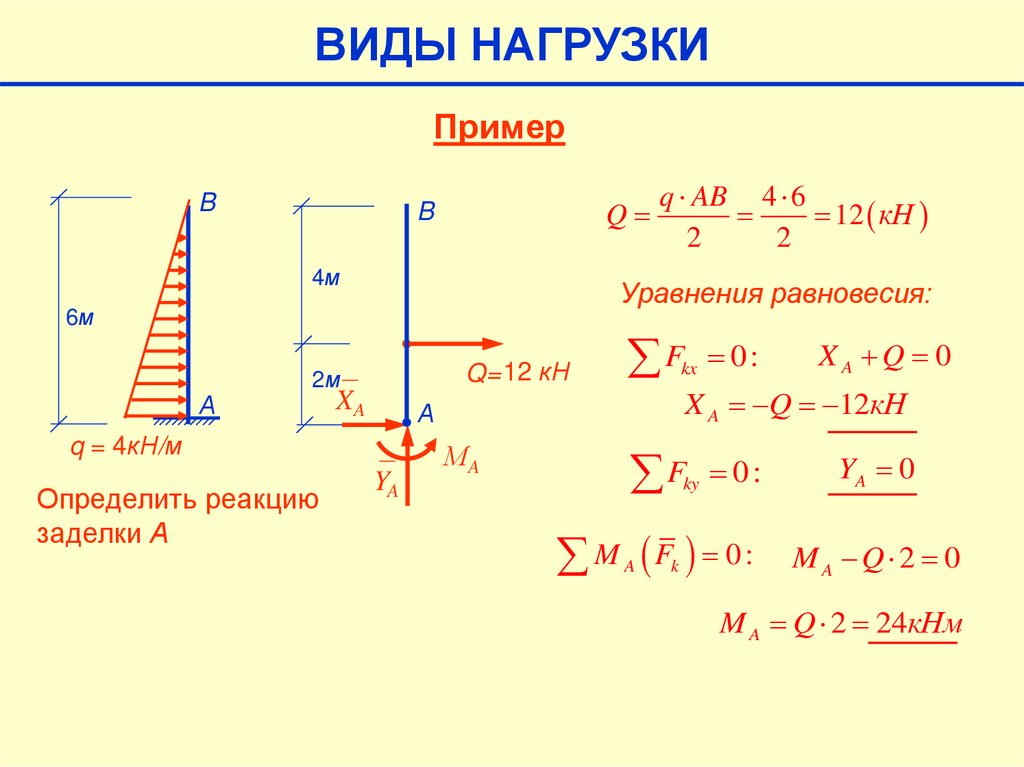
ВИДЫ НАГРУЗКИПример
B
Q
B
4м
Уравнения равновесия:
6м
А
Q= 12 кН
2м
XA
F 0:
kx
YA
МA
XA Q 0
X A Q 12кН
А
q = 4кН/м
Определить реакцию
заделки А
q AB 4 6
12 кН
2
2
F 0:
ky
M F 0:
A
k
YA 0
MA Q 2 0
M A Q 2 24кНм
62.
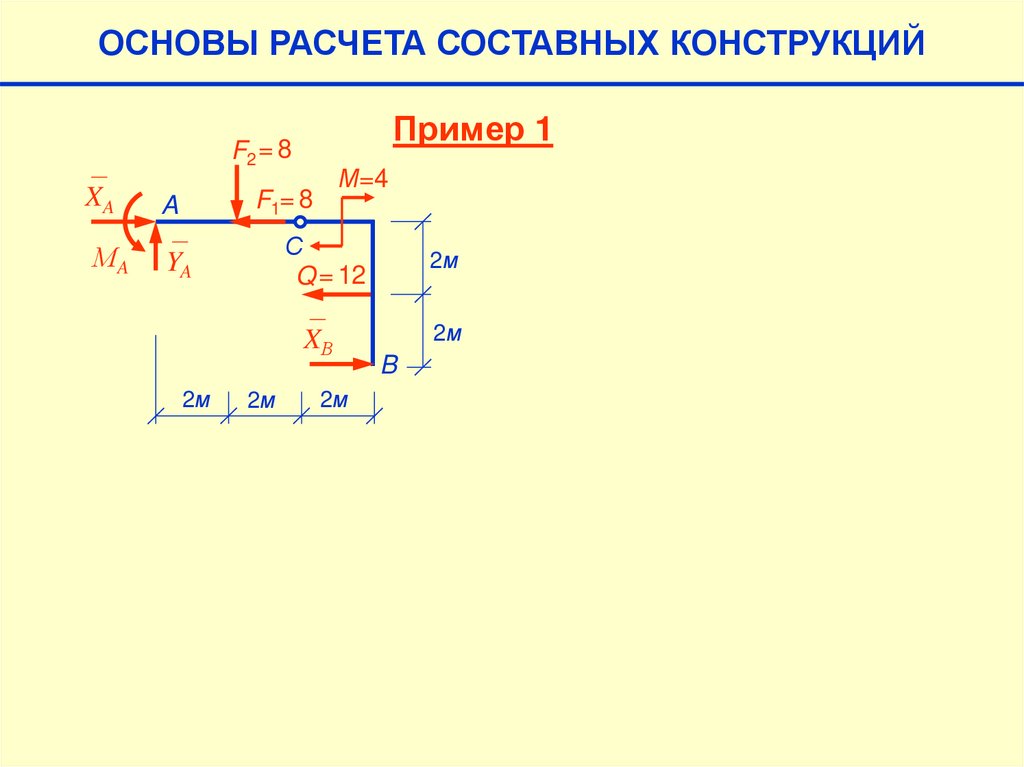
4. Основы расчетасоставных конструкций
63.
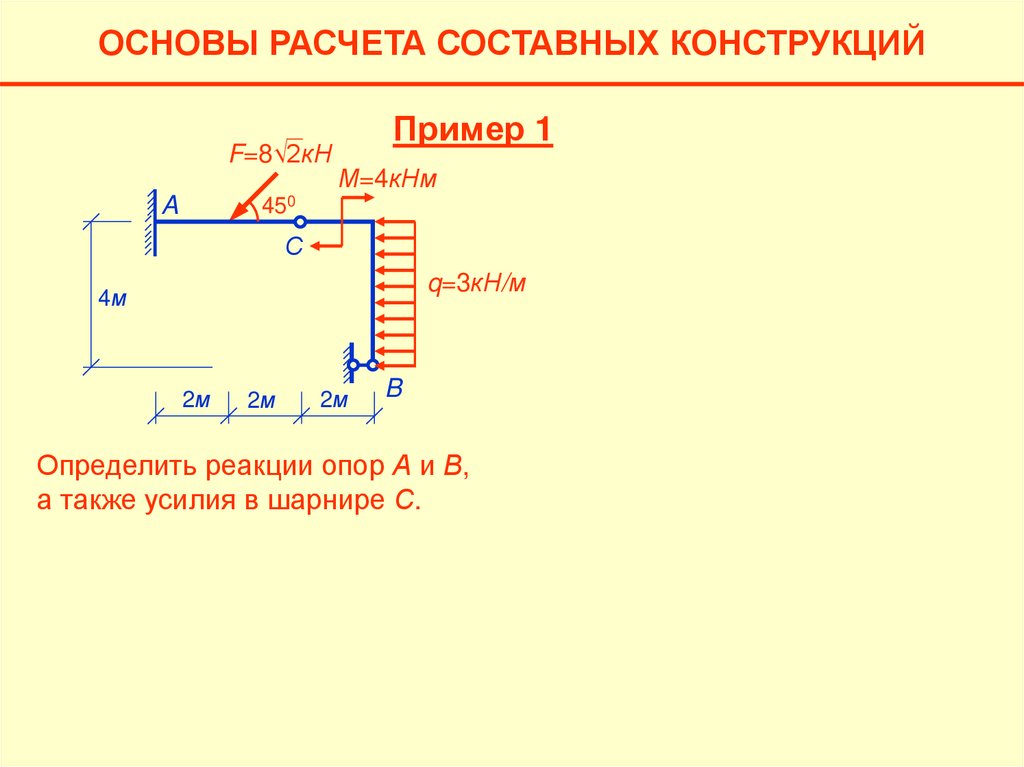
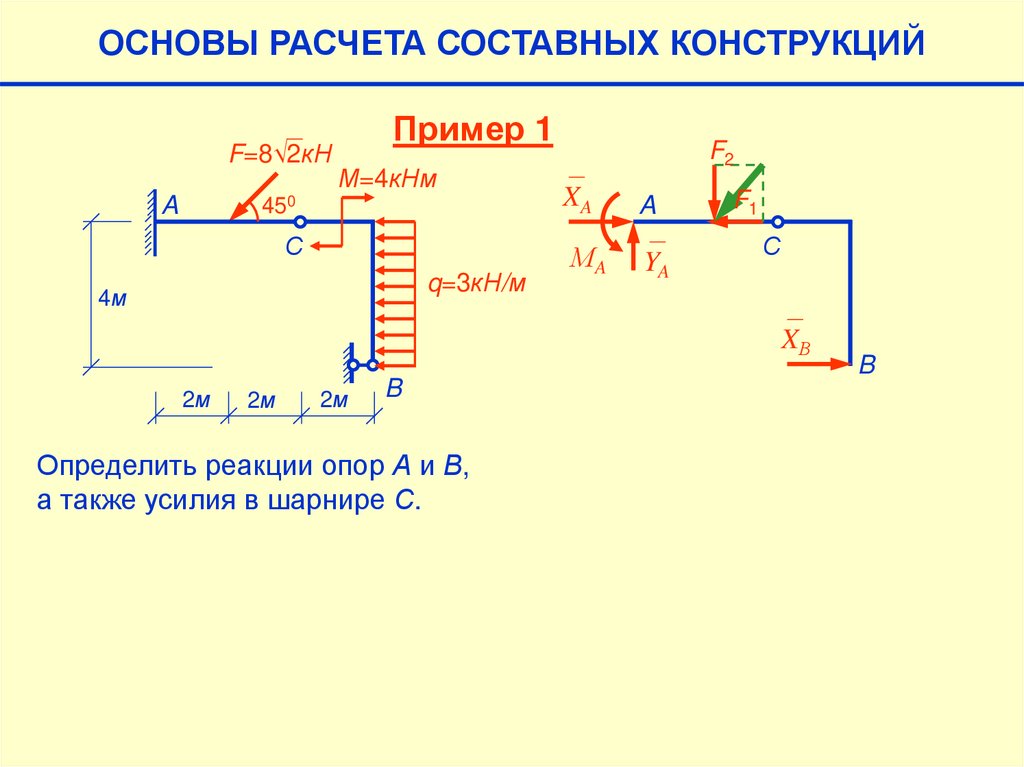
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙF=8√2кН
Пример 1
М=4кНм
450
A
С
q=3кН/м
4м
2м
2м
2м
B
Определить реакции опор А и В,
а также усилия в шарнире С.
64.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙF=8√2кН
A
Пример 1
М=4кНм
F2
450
XA
A
С
МA
YA
q=3кН/м
4м
F1
С
XВ
2м
2м
2м
B
Определить реакции опор А и В,
а также усилия в шарнире С.
B
65.
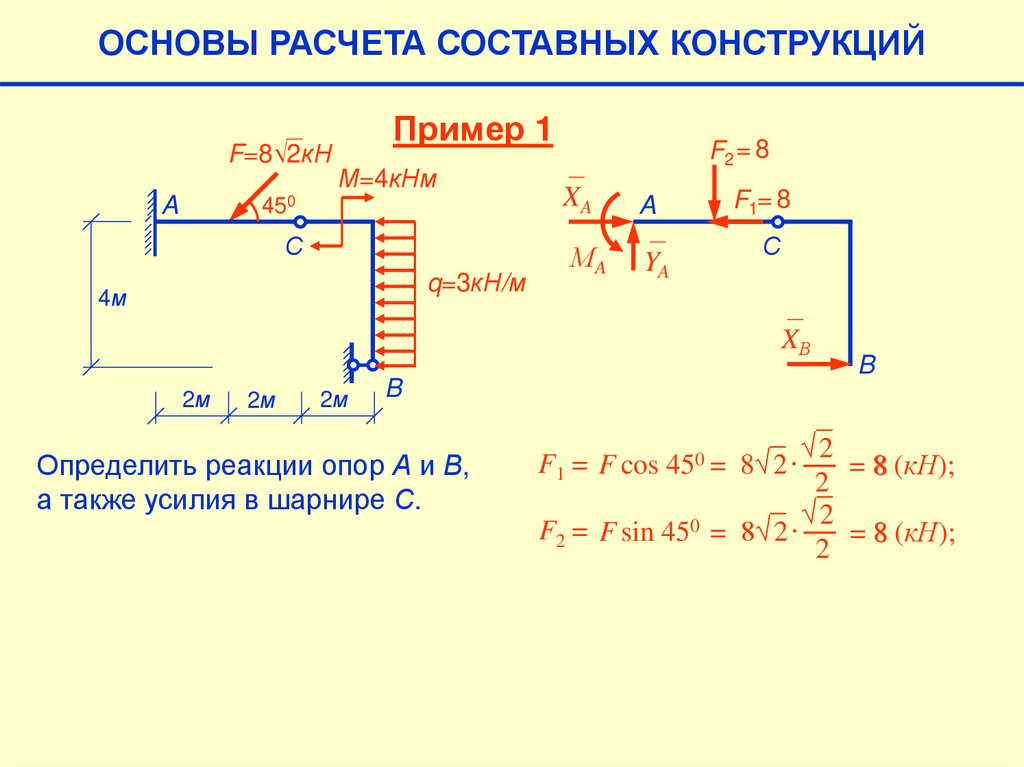
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙF=8√2кН
A
Пример 1
М=4кНм
F2 = 8
450
XA
A
С
МA
YA
q=3кН/м
4м
F1= 8
С
XВ
2м
2м
2м
B
Определить реакции опор А и В,
а также усилия в шарнире С.
B
√2
= 8 (кН);
2
√2
F2 = F sin 450 = 8√2∙
= 8 (кН);
2
F1 = F cos 450 = 8√2∙
66.
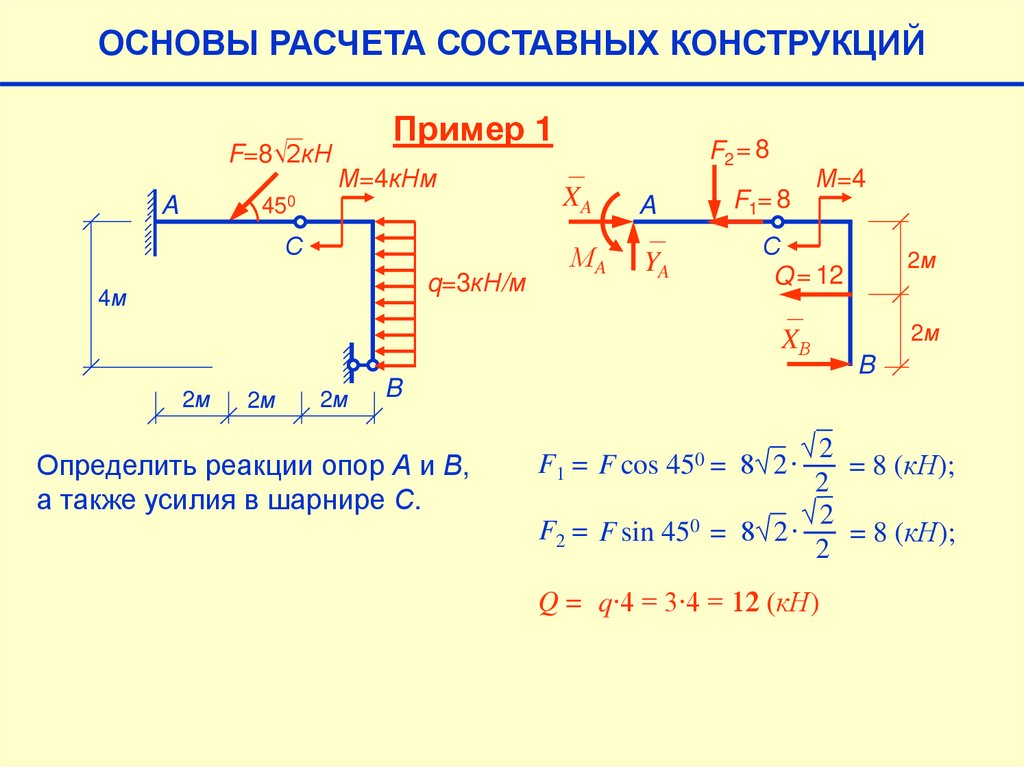
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙF=8√2кН
A
Пример 1
М=4кНм
450
XA
A
С
МA
YA
q=3кН/м
4м
2м
F2 = 8
2м
2м
F1= 8
М=4
С
Q = 12
2м
XВ
2м
B
Определить реакции опор А и В,
а также усилия в шарнире С.
B
√2
= 8 (кН);
2
√2
F2 = F sin 450 = 8√2∙
= 8 (кН);
2
F1 = F cos 450 = 8√2∙
Q = q∙4 = 3∙4 = 12 (кН)
67.
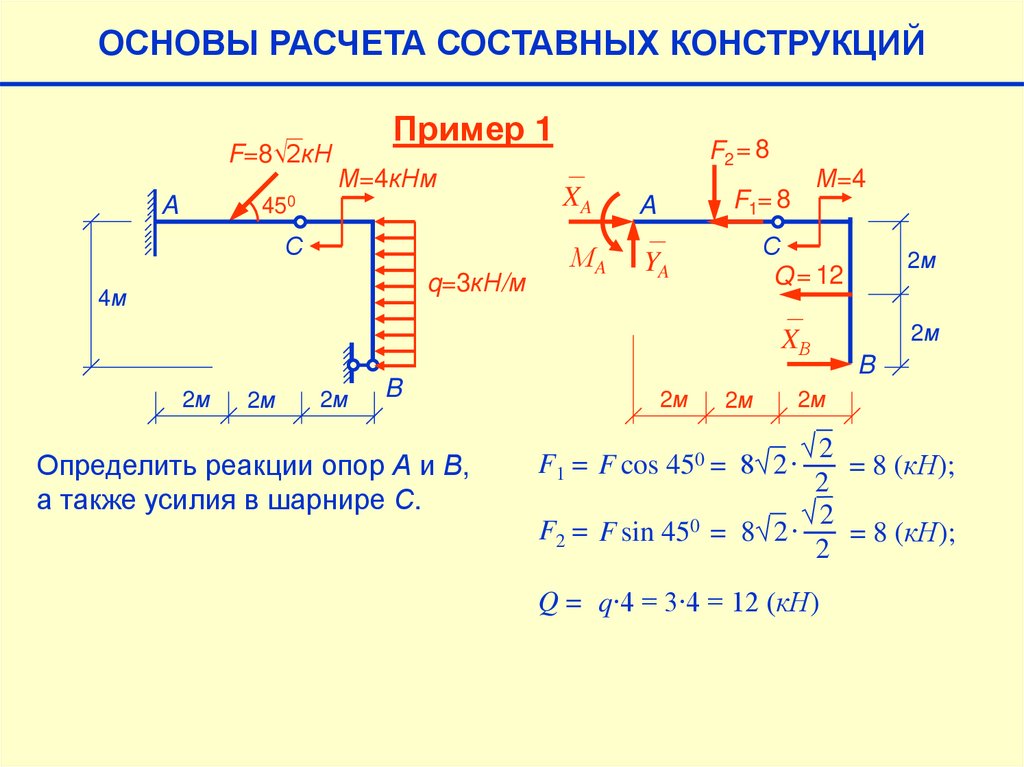
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙF=8√2кН
A
Пример 1
М=4кНм
450
XA
A
С
МA
YA
q=3кН/м
4м
2м
F2 = 8
2м
2м
B
Определить реакции опор А и В,
а также усилия в шарнире С.
М=4
F1= 8
2м
С
Q = 12
2м
XВ
2м
2м
B
2м
√2
= 8 (кН);
2
√2
F2 = F sin 450 = 8√2∙
= 8 (кН);
2
F1 = F cos 450 = 8√2∙
Q = q∙4 = 3∙4 = 12 (кН)
68.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙF=8√2кН
A
Пример 1
М=4кНм
450
XA
A
С
МA
YA
q=3кН/м
4м
2м
F2 = 8
2м
2м
B
Определить реакции опор А и В,
а также усилия в шарнире С.
М=4
F1= 8
2м
С
Q = 12
2м
XВ
2м
2м
B
2м
√2
= 8 (кН);
2
√2
F2 = F sin 450 = 8√2∙
= 8 (кН);
2
F1 = F cos 450 = 8√2∙
Q = q∙4 = 3∙4 = 12 (кН)
69.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
М=4
F1= 8
2м
2м
С
Q = 12
2м
XВ
2м
2м
B
70.
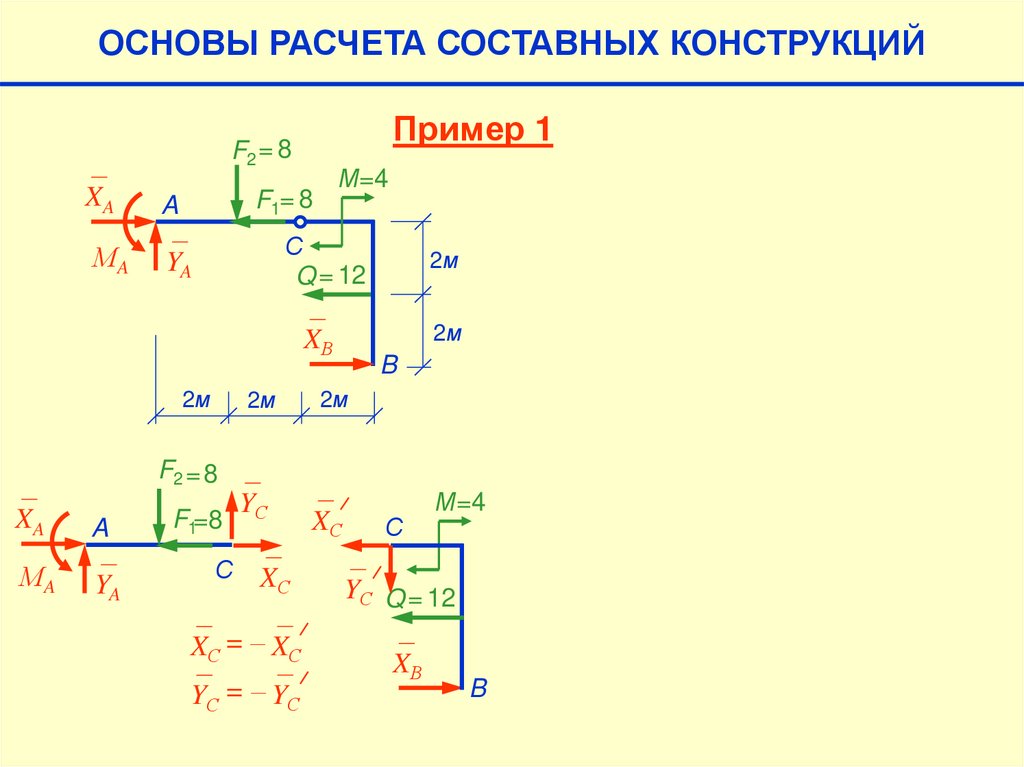
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
М=4
F1= 8
2м
С
Q = 12
2м
XВ
2м
2м
B
2м
F2 = 8
XA
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
XС
С
М=4
YС Q = 12
XВ
B
71.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
М=4
F1= 8
2м
С
Q = 12
2м
XВ
2м
2м
B
2м
F2 = 8
XA
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
4
XС
С
М=4
YС Q = 12
XВ
B
72.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
М=4
F1= 8
2м
С
Q = 12
2м
XВ
2м
2м
B
2м
5
F2 = 8
XA
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
XС
С
М=4
YС Q = 12
XВ
B
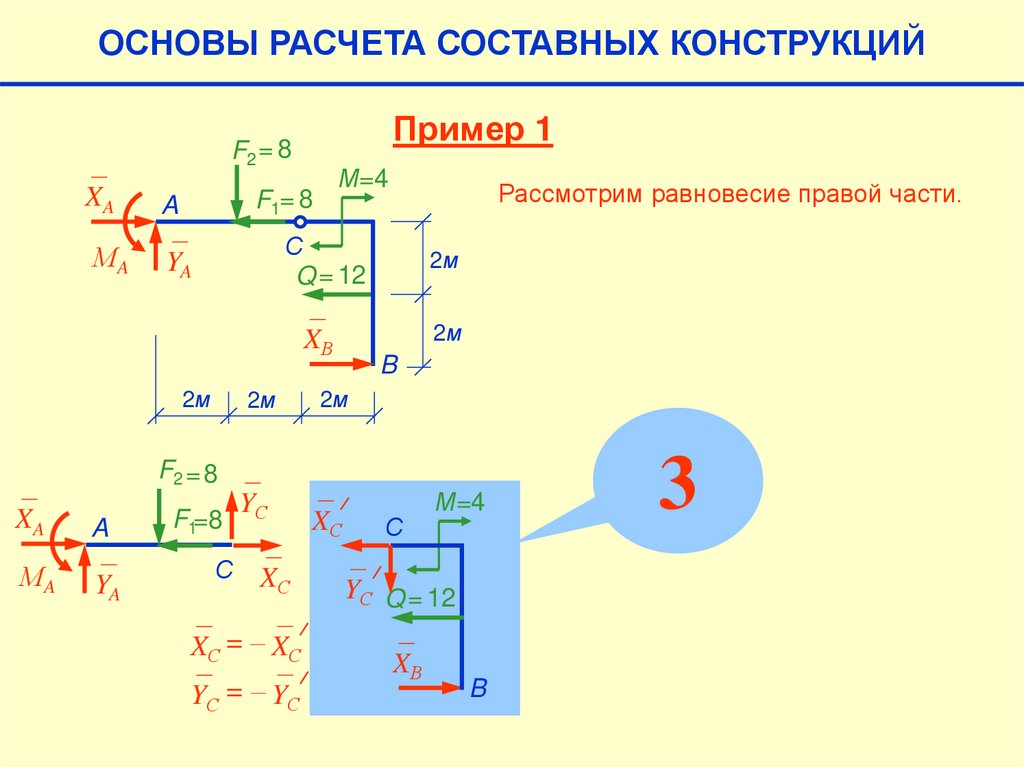
73.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
М=4
F1= 8
2м
Рассмотрим равновесие правой части.
С
Q = 12
2м
XВ
2м
2м
B
2м
F2 = 8
XA
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
XС
С
М=4
YС Q = 12
XВ
B
3
74.
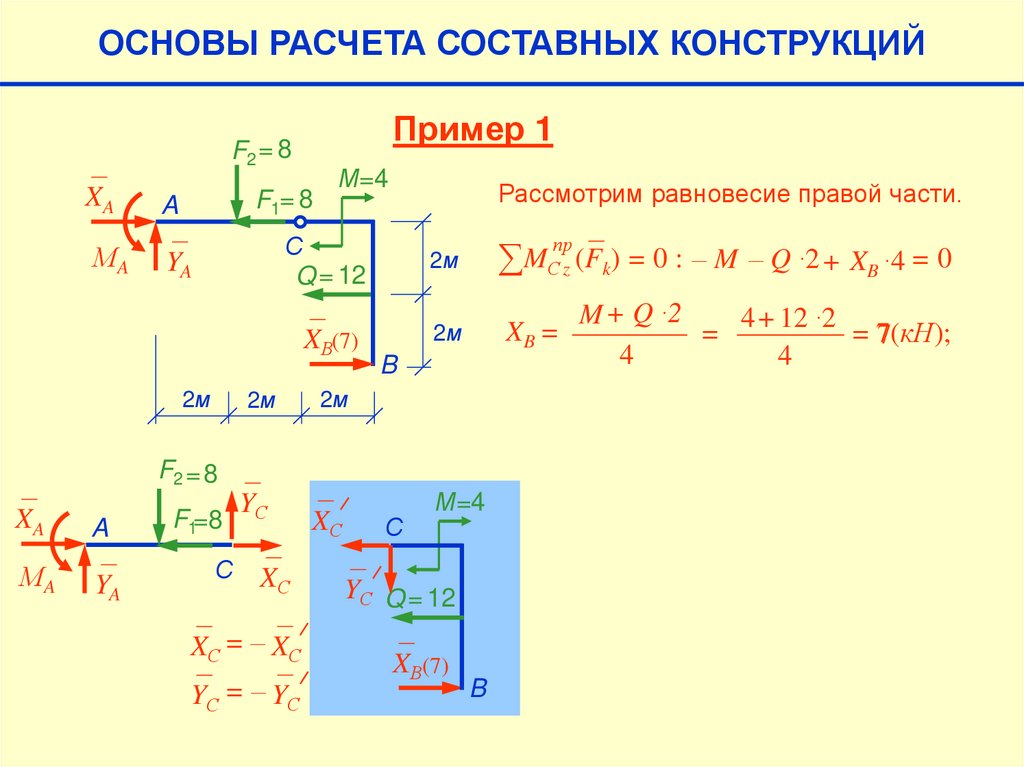
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
F1= 8
М=4
Рассмотрим равновесие правой части.
С
Q = 12
XВ(7)
2м
2м
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
∑ MСпрz (Fk) = 0 : – M – Q ∙2 + XB ∙4 = 0
2м
XB =
B
2м
F2 = 8
XA
2м
XС
С
М=4
YС Q = 12
XВ(7)
B
M + Q ∙2
4+ 12 ∙2
= 7(кН);
=
7
4
4
75.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
F1= 8
М=4
Рассмотрим равновесие правой части.
С
Q = 12
XВ(7)
2м
2м
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
∑ MСпрz (Fk) = 0 : – M – Q ∙2 + XB ∙4 = 0
2м
XB =
B
M + Q ∙2
4+ 12 ∙2
= 7(кН);
=
4
4
∑ Fkxпр= 0 : – XС – Q + XB = 0
2м
F2 = 8
XA
2м
XС (-5)С
М=4
YС Q = 12
XВ(7)
B
XС = – Q + XB = – 12 + 7 = – 5(кН);
76.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
F1= 8
М=4
Рассмотрим равновесие правой части.
С
Q = 12
XВ(7)
2м
2м
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
∑ MСпрz (Fk) = 0 : – M – Q ∙2 + XB ∙4 = 0
2м
XB =
B
M + Q ∙2
4+ 12 ∙2
= 7(кН);
=
4
4
∑ Fkxпр= 0 : – XС – Q + XB = 0
2м
F2 = 8
XA
2м
XС (-5)С
М=4
0
∑ Fkyпр= 0 : – YС = 0 => YС = 0.
YС Q = 12
(0)
XВ(7)
XС = – Q + XB = – 12 + 7 = –5(кН);
B
77.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
F1= 8
М=4
Рассмотрим равновесие правой части.
С
Q = 12
XВ(7)
2м
2м
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
∑ MСпрz (Fk) = 0 : – M – Q ∙2 + XB ∙4 = 0
2м
XB =
B
M + Q ∙2
4+ 12 ∙2
= 7(кН);
=
4
4
∑ Fkxпр= 0 : – XС – Q + XB = 0
2м
F2 = 8
XA
2м
XС (-5)С
М=4
∑ Fkyпр= 0 : – YС = 0 => YС = 0.
YС Q = 12
(0)
XВ(7)
XС = – Q + XB = – 12 + 7 = –5(кН);
B
78.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
F1= 8
М=4
Рассмотрим равновесие правой части.
С
Q = 12
XВ(7)
2м
2м
A
МA
YA
F1=8
С
YС
XС
XС = – XС
Y С = – YС
∑ MСпрz (Fk) = 0 : – M – Q ∙2 + XB ∙4 = 0
2м
XB =
B
M + Q ∙2
4+ 12 ∙2
= 7(кН);
=
4
4
∑ Fkxпр= 0 : – XС – Q + XB = 0
2м
F2 = 8
XA
2м
XС (-5)С
М=4
∑ Fkyпр= 0 : – YС = 0 => YС = 0.
YС Q = 12
Напоминание
(0)
XВ(7)
XС = – Q + XB = – 12 + 7 = –5(кН);
B
a = – b =>
1). | a | = | b |
2). a ↑↓ b
79.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
F1= 8
М=4
Рассмотрим равновесие правой части.
С
Q = 12
XВ(7)
2м
2м
A
МA
YA
F1=8
С
YС (0)
Y С = – YС
2м
XB =
M + Q ∙2
4+ 12 ∙2
= 7(кН);
=
4
4
∑ Fkxпр= 0 : – XС – Q + XB = 0
2м
XС (-5)С
XС (-5) Y
XС = – XС
∑ MСпрz (Fk) = 0 : – M – Q ∙2 + XB ∙4 = 0
B
F2 = 8
XA
2м
М=4
∑ Fkyпр= 0 : – YС = 0 => YС = 0.
С Q = 12
Напоминание
(0)
XВ(7)
XС = – Q + XB = – 12 + 7 = –5(кН);
B
a = – b =>
1). | a | = | b |
2). a ↑↓ b
80.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA
A
МA
YA
F1= 8
М=4
Рассмотрим равновесие правой части.
С
Q = 12
XВ(7)
2м
2м
A
МA
YA
F1=8
С
YС (0)
Y С = – YС
2м
XB =
M + Q ∙2
4+ 12 ∙2
= 7(кН);
=
4
4
∑ Fkxпр= 0 : – XС – Q + XB = 0
2м
XС (-5)С
XС (-5) Y
XС = – XС
∑ MСпрz (Fk) = 0 : – M – Q ∙2 + XB ∙4 = 0
B
F2 = 8
XA
2м
М=4
∑ Fkyпр= 0 : – YС = 0 => YС = 0.
С Q = 12
(0)
XВ(7)
XС = – Q + XB = – 12 + 7 = 5(кН);
B
81.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA(13) A
МA
F1= 8
М=4
Рассмотрим равновесие левой части.
С
Q = 12
YA
2м
B
2м
F2 = 8
(13)
XA
A
МA
YA
F1=8
С
YС (0)
XА = F1 – XC = 8 + 5 = 13 (кН);
2м
XВ(7)
2м
∑ Fkxлев= 0 : XА – F1 + XC = 0
2м
XС (-5)С
XС (-5) Y
М=4
С Q = 12
(0)
XВ(7)
B
82.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA(13) A
МA
F1= 8
М=4
С
Q = 12
YA (8)
2м
(13)
A
МA
YA (8)
F1=8
С
XА = F1 – XC = 8 + 5 = 13 (кН);
B
∑ Fkyлев= 0 : YА – F2 + YC = 0
2м
YА = F2 = 8
(кН);
F2 = 8
XA
∑ Fkxлев= 0 : XА – F1 + XC = 0
2м
2м
XВ(7)
2м
Рассмотрим равновесие левой части.
YС (0)
XС (-5)С
XС (-5) Y
М=4
С Q = 12
(0)
XВ(7)
B
83.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA(13) A
МA
(16)
F1= 8
М=4
С
Q = 12
YA (8)
2м
(13)
МA
(16)
A
YA (8)
F1=8
С
YС (0)
XА = F1 – XC = 8 + 5 = 13 (кН);
B
∑ Fkyлев= 0 : YА – F1 + YC = 0
2м
F2 = 8
XA
∑ Fkxлев= 0 : XА – F1 + XC = 0
2м
2м
XВ(7)
2м
Рассмотрим равновесие левой части.
XС (-5)С
XС (-5) Y
М=4
YА = F1 = 8
(кН);
лев
∑ MА z (Fk) = 0 : MА – F2 ∙2 + YC ∙4 = 0
MА = F2 ∙ 2 = 8 ∙2 = 16 (кНм)
С Q = 12
(0)
XВ(7)
B
84.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA(13) A
МA
(16)
F1= 8
М=4
С
Q = 12
YA (8)
2м
(13)
МA
(16)
A
YA (8)
F1=8
С
YС (0)
XА = F1 – XC = 8 + 5= 13 (кН);
B
∑ Fkyлев= 0 : YА – F1 + YC = 0
2м
F2 = 8
XA
∑ Fkxлев= 0 : XА – F1 + XC = 0
2м
2м
XВ(7)
2м
Проверка. левой части.
Рассмотрим равновесие
XС (-5)С
XС (-5) Y
М=4
YА = F1 = 8
(кН);
лев
∑ MА z (Fk) = 0 : MА – F2 ∙2 + YC ∙4 = 0
MА = F2 ∙ 2 = 8 ∙2 = 16 (кНм)
С Q = 12
(0)
XВ(7)
B
85.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA(13) A
МA
(16)
F1= 8
YA (8)
2м
М=4
Проверка
Рассмотрим равновесие конструкции в целом
С
Q = 12
2м
XВ(7)
2м
2м
∑ Fkxцел= XA – F1 – Q + XB =
∑ Fkyцел= YA – F2 = 8 – 8 = 0
2м
F2 = 8
(13)
XA
A
МA
YA (8)
(16)
F1=8
С
YС (0)
= 13 – 8 – 12 + 7 = 0
B
XС (-5)С
XС (-5) Y
М=4
= МА – F2 ∙2 – М – Q ∙2 +XB∙4 =
С Q = 12
= 16 – 8 ∙2 – 4 – 12 ∙2 + 7∙4 = 0
(0)
XВ(7)
∑ MАцел
z (Fk) =
B
86.
ОСНОВЫ РАСЧЕТА СОСТАВНЫХ КОНСТРУКЦИЙПример 1
F2 = 8
XA(13) A
МA
(16)
F1= 8
YA (8)
2м
М=4
Проверка
Рассмотрим равновесие конструкции в целом
С
Q = 12
2м
XВ(7)
2м
2м
∑ Fkxцел= XA – F1 – Q + XB =
∑ Fkyцел= YA – F2 = 8 – 8 = 0
2м
F2 = 8
(13)
XA
A
МA
YA (8)
(16)
F1=8
С
YС (0)
= 13 – 8 – 12 + 7 = 0
B
XС (-5)С
XС (-5) Y
М=4
= МА – F2 ∙2 – М – Q ∙2 +XB∙4 =
С Q = 12
= 16 – 8 ∙2 – 4 – 12 ∙2 + 7∙4 = 0
(0)
XВ(7)
∑ MАцел
z (Fk) =
B
87.
5. Классификация расчётныхсхем стержневых систем.
Кинематический анализ.
88. Классификация расчётных схем
Основные типы стержневых систем1.Балочные системы (балки)
2.Арочные системы (арки)
3.Рамные системы (рамы)
4.Фермы
5.Висячие системы
6.Комбинированные системы
Классификация по кинематическому признаку
1.Геометрически неизменяемые системы – перемещения узлов
возможны только при условии деформации элементов
2.Геометрически изменяемые системы – перемещения узлов не
связаны с деформированием элементов (механизмы)
3.Мгновено изменяемые системы – в системах могут возникать
бесконечно малые перемещения без деформации элементов
Классификация по статическому признаку
1.Статически определимые системы- усилия во всех элементах
могут быть определены с помощью одних уравнений равновесия
2.Статически неопределимые системы – все остальные
89.
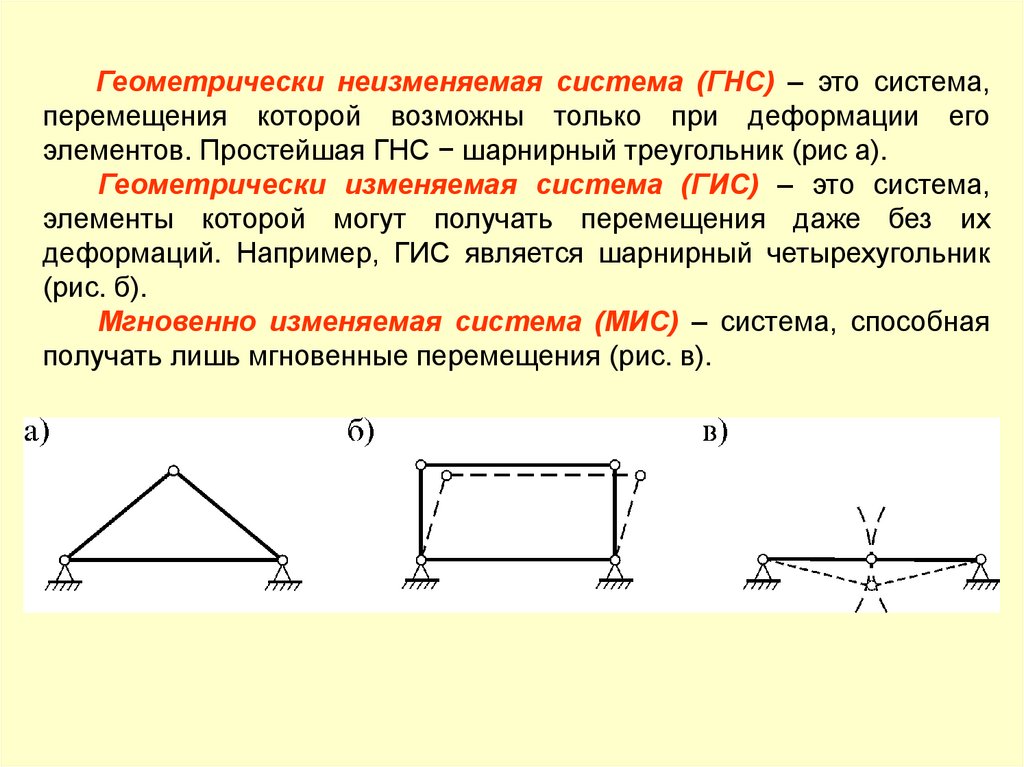
Геометрически неизменяемая система (ГНС) – это система,перемещения которой возможны только при деформации его
элементов. Простейшая ГНС − шарнирный треугольник (рис а).
Геометрически изменяемая система (ГИС) – это система,
элементы которой могут получать перемещения даже без их
деформаций. Например, ГИС является шарнирный четырехугольник
(рис. б).
Мгновенно изменяемая система (МИС) – система, способная
получать лишь мгновенные перемещения (рис. в).
90. Кинематический анализ расчётных схем
91. Степень свободы. Кинематические связи
Количественная оценка кинематических свойств системы основана напонятии степени свободы как направления возможного независимого
перемещения.
Число степеней свободы (W) – это минимальное число независимых
параметров, необходимых для определения положения всех точек системы.
Такими параметрами могут быть перемещения отдельных точек, углы
поворота элементов и др.
Число степеней свободы простых систем можно определять путем
задания ее элементам возможных перемещений (рис. а, б, в):
92. Структурный анализ расчётных схем
Двухдисковое соединениеСтепень взаимной подвижности двух дисков равна трём. Следовательно,
взаимная неподвижность двухдискового соединения обеспечивается одним
шарниром и одной одиночной связи, линия действия которой не пересекает
шарнир
Геометрически неизменяемая система
Мгновенно изменяемая система
Геометрически изменяемая система
93.
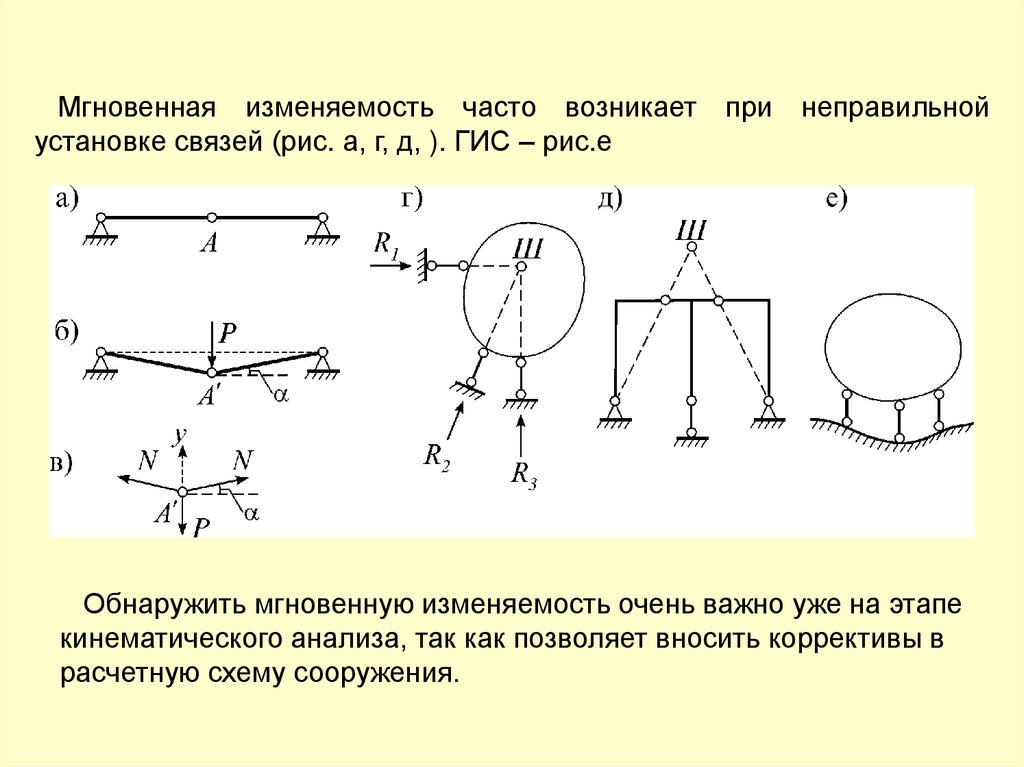
Мгновенная изменяемость часто возникает при неправильнойустановке связей (рис. а, г, д, ). ГИС – рис.е
Обнаружить мгновенную изменяемость очень важно уже на этапе
кинематического анализа, так как позволяет вносить коррективы в
расчетную схему сооружения.
94. Способы образования неизменяемых систем
Выполнение условия W 0 необходимо, но не достаточно. Например,у систем на рис. а, б W=0, но первая из них ГИС, а другая ГНС.
Причиной изменяемости системы а) является неправильная установка
связей. Чтобы она стала неизменяемой, одну связь нужно переставить
(рис. б).
То же самое имеет место и для систем на рис. в и г.
95.
96.
6. Расчёт ферм97. Расчёт фермы. Условие статической определимости.
Ферма называется статически определимой, если число неизвестных равно числу уравнений равновесия, в которые эти неизвестные входят. Для фермы, имеющей nузлов, можно составить 2n независимых уравнений равновесия. В число неизвестных входят N усилий в стержнях фермы и три составляющие реакций внешних опор.
Таким образом, ферма будет статически определимой
при выолнении условия
N = 2n – 3,
которое, как видно, совпадает с условием жёсткости.
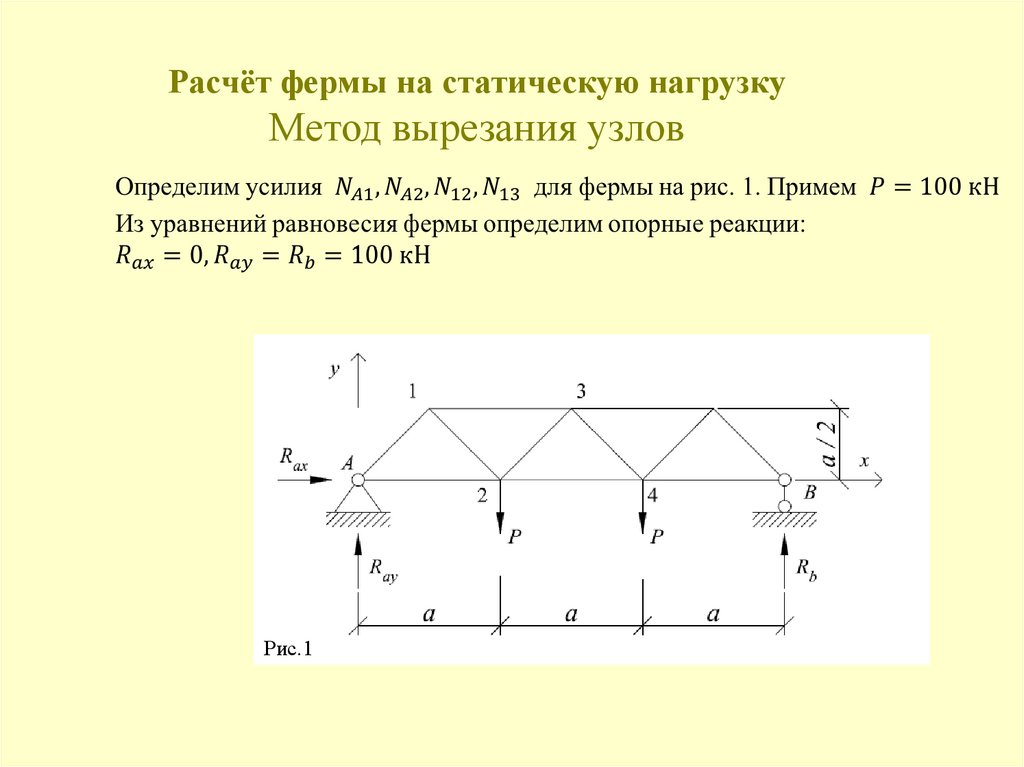
98. Расчёт фермы на статическую нагрузку Метод вырезания узлов
Рис.199. Расчёт фермы на статическую нагрузку Метод вырезания узлов
Рис.2100. Расчёт фермы на статическую нагрузку Метод вырезания узлов
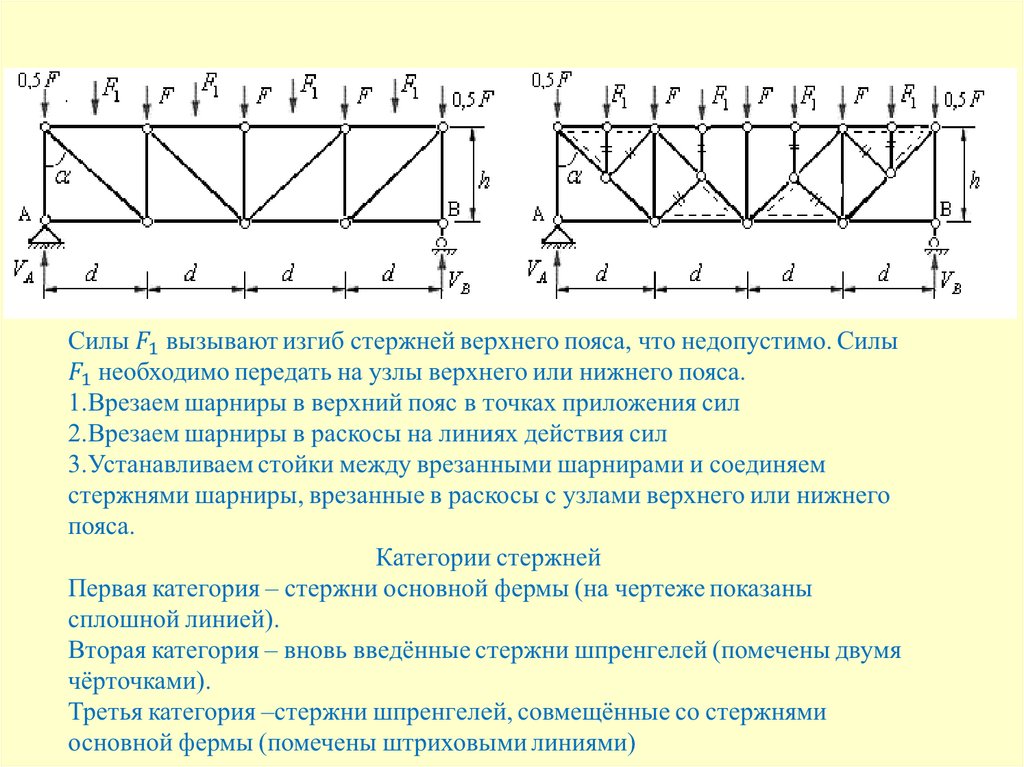
Рис.3101. Расчёт фермы на статическую нагрузку Метод сквозных сечений
Этим методом удобно пользоваться для определения усилий вотдельных стержнях фермы.
Идея метода состоит в том, что ферма разделяется сечением на две
части и рассматривается равновесие одной из частей фермы.
Сечение проводится по трём стержням фермы, в которых требуется
определить усилия.
Действие отброшенной части фермы заменяют соответствующими
реакциями (искомыми усилиями стержней), направляя их вдоль
разрезанных стержней, от узлов, т.е. считая их растянутыми
102. Расчёт фермы на статическую нагрузку Метод сквозных сечений
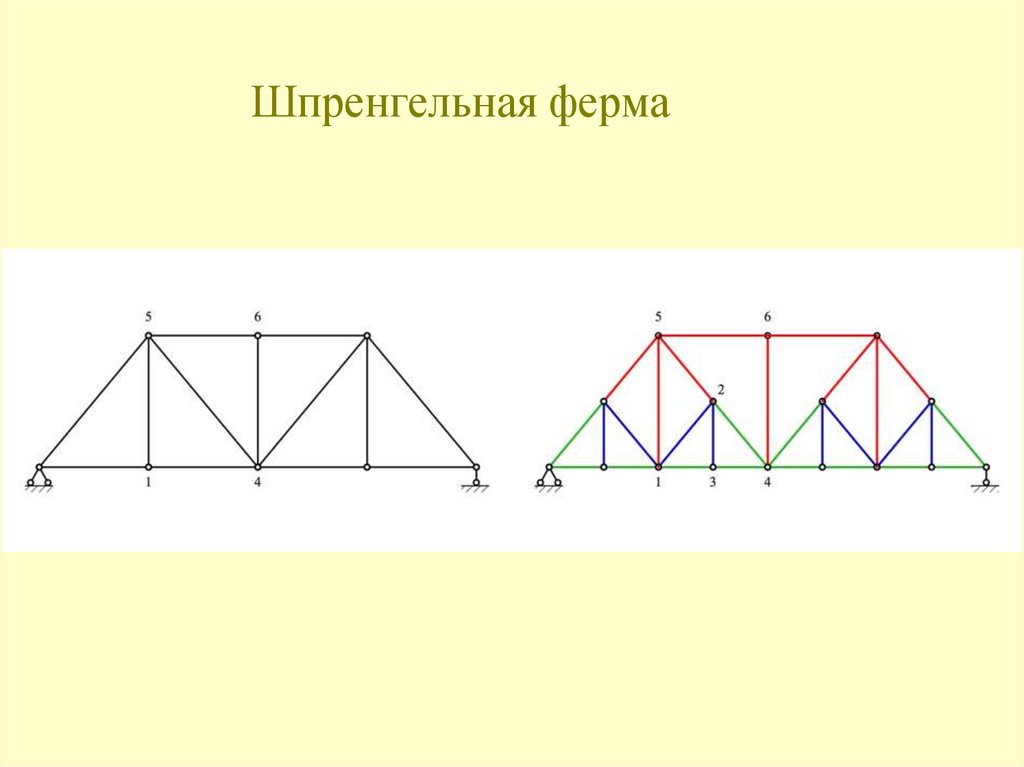
Рис.4103. Шпренгельная ферма
104.
105.
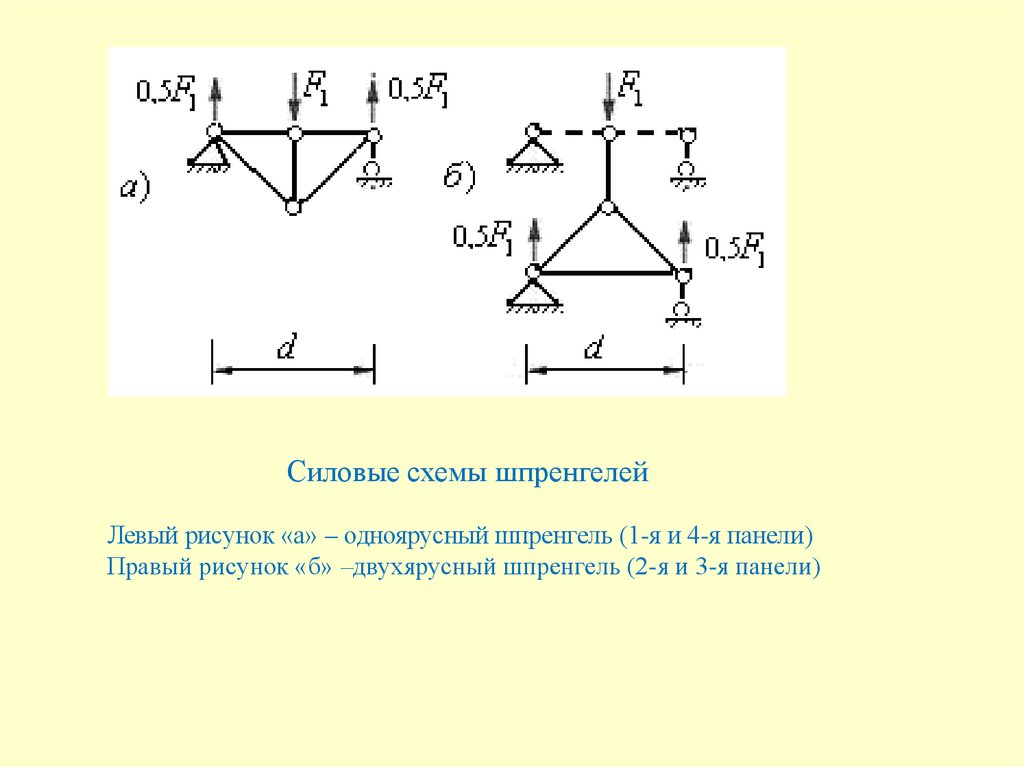
Силовые схемы шпренгелейЛевый рисунок «а» – одноярусный шпренгель (1-я и 4-я панели)
Правый рисунок «б» –двухярусный шпренгель (2-я и 3-я панели)
106. Шпренгельные фермы. Расчёт на статическую нагрузку
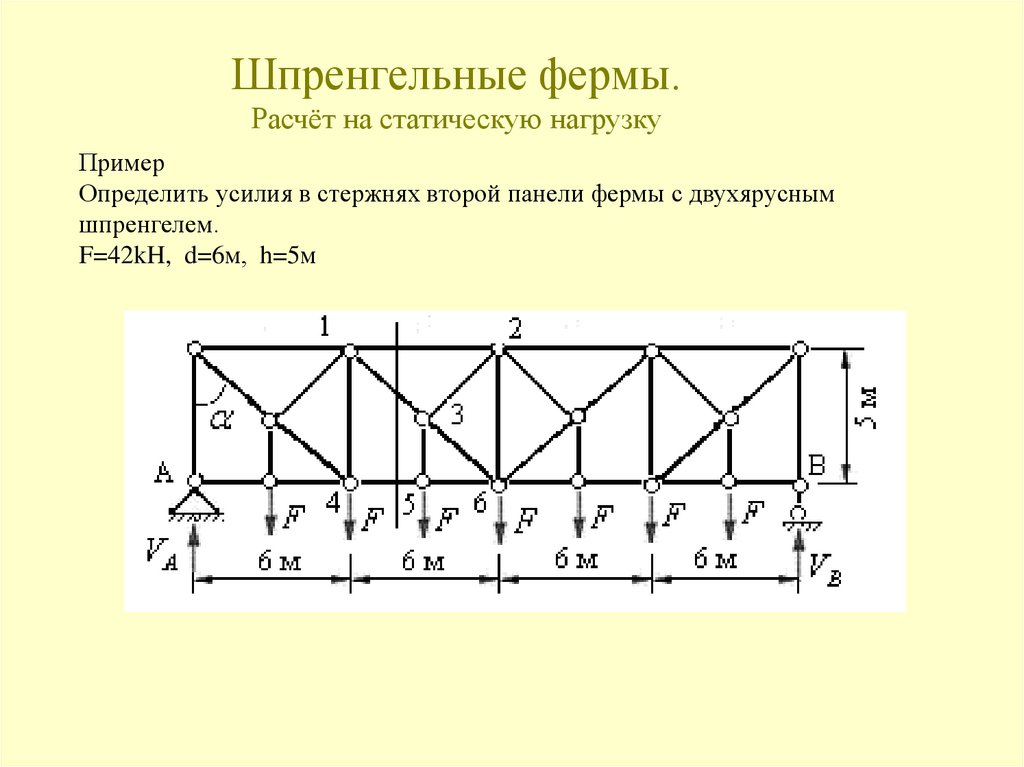
107. Шпренгельные фермы. Расчёт на статическую нагрузку
ПримерОпределить усилия в стержнях второй панели фермы с двухярусным
шпренгелем.
F=42kH, d=6м, h=5м
108. Шпренгельные фермы. Расчёт на статическую нагрузку
109. Шпренгельные фермы. Расчёт на статическую нагрузку
110. Шпренгельные фермы. Расчёт на статическую нагрузку
111. Шпренгельные фермы. Расчёт на статическую нагрузку
112. Шпренгельные фермы. Расчёт на статическую нагрузку
113.
7. Расчёт многопролётныхстатически определимых балок
и рам
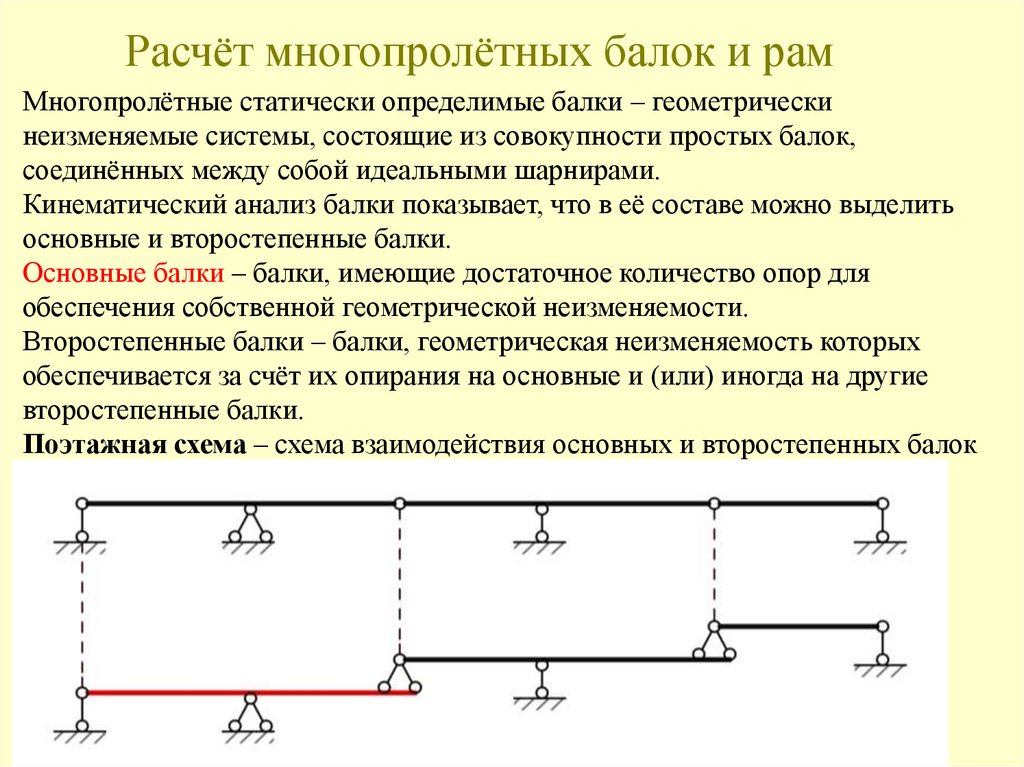
114. Расчёт многопролётных балок и рам
Многопролётные статически определимые балки – геометрическинеизменяемые системы, состоящие из совокупности простых балок,
соединённых между собой идеальными шарнирами.
Кинематический анализ балки показывает, что в её составе можно выделить
основные и второстепенные балки.
Основные балки – балки, имеющие достаточное количество опор для
обеспечения собственной геометрической неизменяемости.
Второстепенные балки – балки, геометрическая неизменяемость которых
обеспечивается за счёт их опирания на основные и (или) иногда на другие
второстепенные балки.
Поэтажная схема – схема взаимодействия основных и второстепенных балок
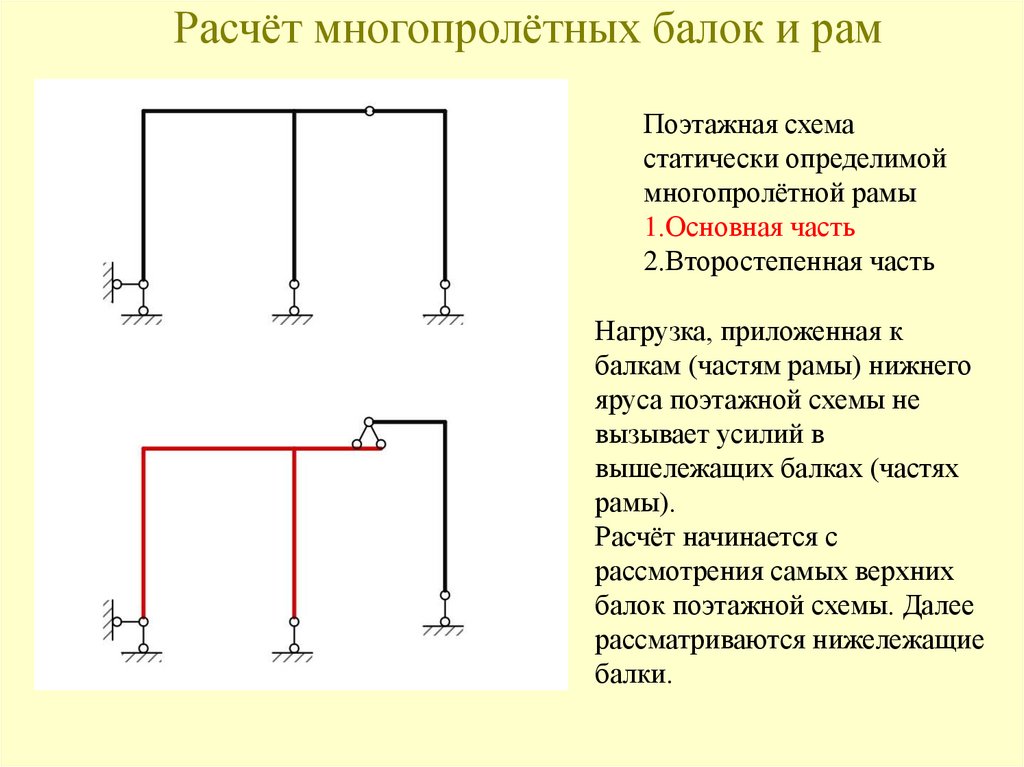
115. Расчёт многопролётных балок и рам
Поэтажная схемастатически определимой
многопролётной рамы
1.Основная часть
2.Второстепенная часть
Нагрузка, приложенная к
балкам (частям рамы) нижнего
яруса поэтажной схемы не
вызывает усилий в
вышележащих балках (частях
рамы).
Расчёт начинается с
рассмотрения самых верхних
балок поэтажной схемы. Далее
рассматриваются нижележащие
балки.
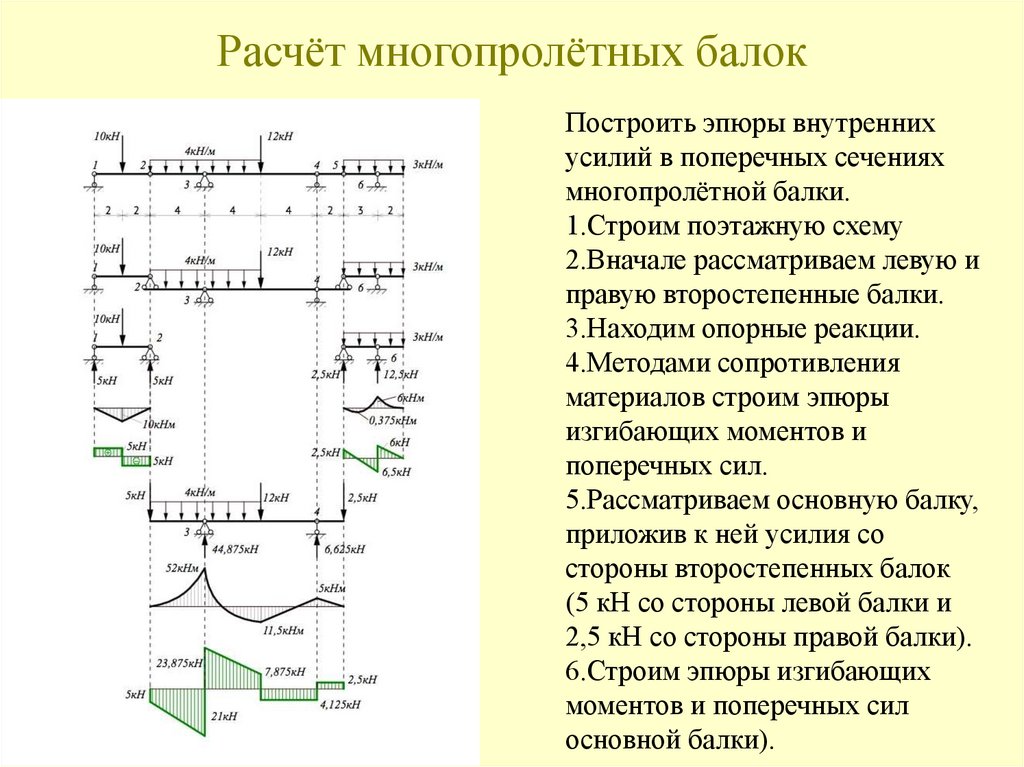
116. Расчёт многопролётных балок
Построить эпюры внутреннихусилий в поперечных сечениях
многопролётной балки.
1.Строим поэтажную схему
2.Вначале рассматриваем левую и
правую второстепенные балки.
3.Находим опорные реакции.
4.Методами сопротивления
материалов строим эпюры
изгибающих моментов и
поперечных сил.
5.Рассматриваем основную балку,
приложив к ней усилия со
стороны второстепенных балок
(5 кН со стороны левой балки и
2,5 кН со стороны правой балки).
6.Строим эпюры изгибающих
моментов и поперечных сил
основной балки).
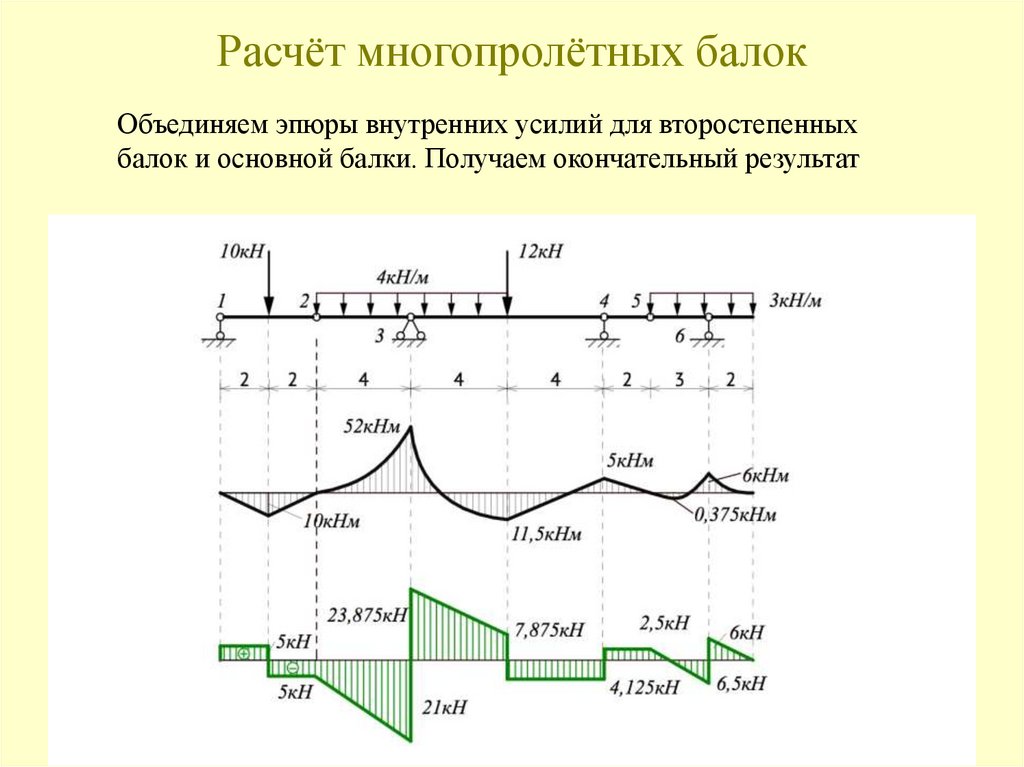
117. Расчёт многопролётных балок
Объединяем эпюры внутренних усилий для второстепенныхбалок и основной балки. Получаем окончательный результат
118.
8. Линии влияния. Построениелиний влияния.
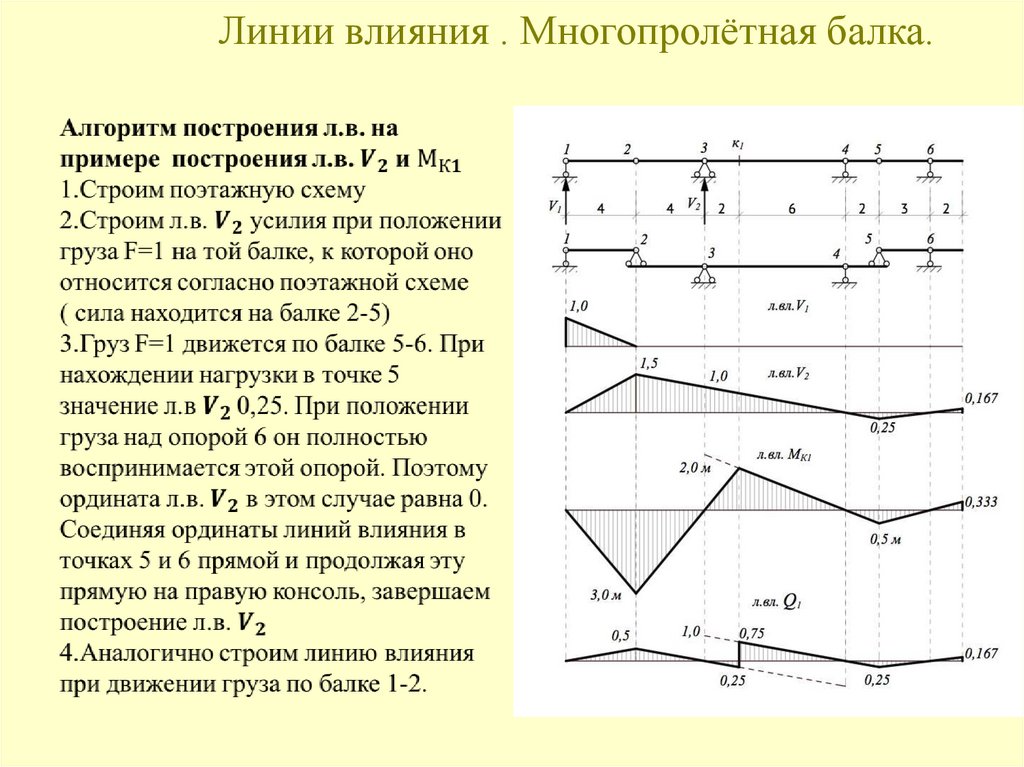
119. Линии влияния
Линия влияния (ЛВ) – это график изменения параметра конструкции(внутреннего усилия, прогиба, угла поворота и т.д.) в определенном месте
(сечении) конструкции от единичной безразмерной силы P=1, которая
движется по конструкции без ускорения, сохраняя при этом постоянное
направление. Понятия ЛВ и эпюры нельзя путать, потому что эпюра
показывает значение внутреннего усилия для всех точек (сечений) от
постоянной нагрузки, а ЛВ показывает значение внутреннего усилия от
подвижной единичной силы P=1 только для одного сечения.
Сущность метода: искомая величина (внутреннее усилие, реакция и др.)
определяется как функция от положения подвижной единичной силы;
строится график зависимости искомой величины от положения единичной
силы, а затем при необходимости находится максимальное значение искомой
величины.
120. Линии влияния. Балка
121. Линии влияния внутренних усилий. Балка
122. Линии влияния . Многопролётная балка.
123. Линии влияния . Многопролётная балка.
124. Линии влияния . Многопролётная балка.
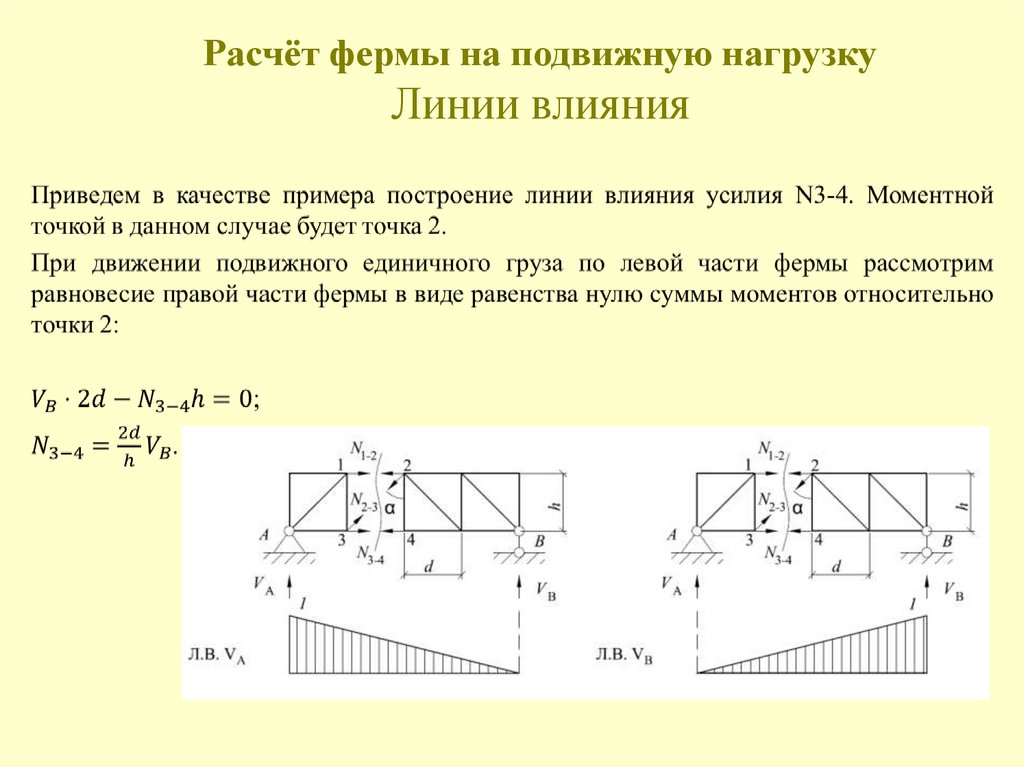
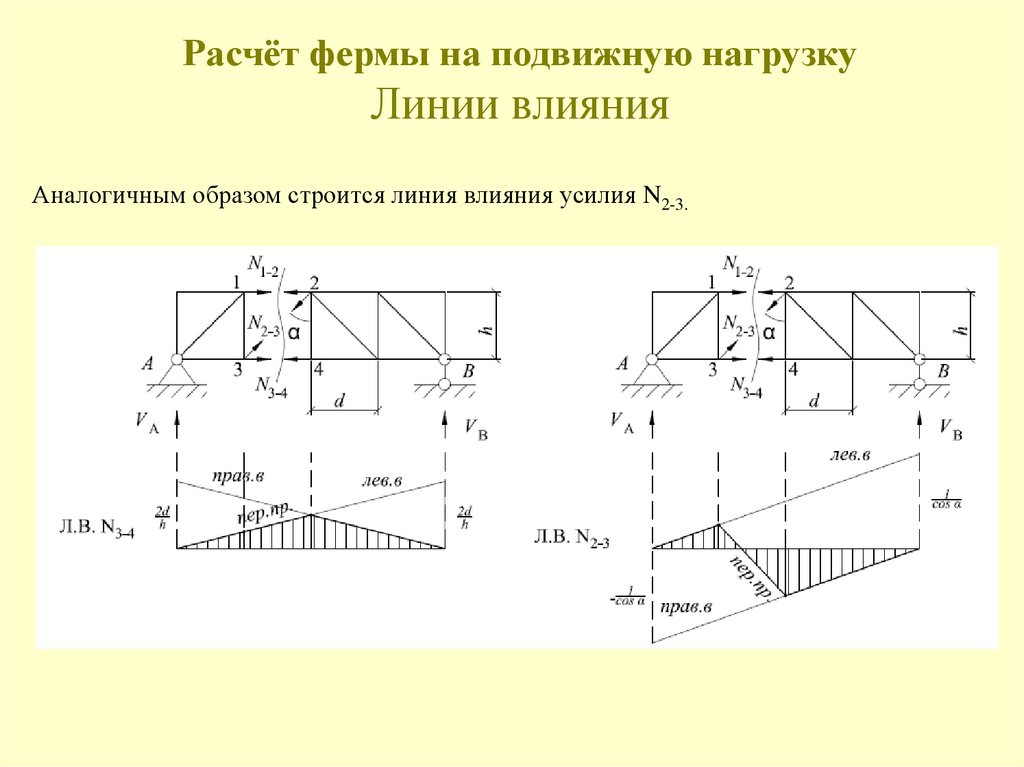
125. Расчёт фермы на подвижную нагрузку Линии влияния
126. Расчёт фермы на подвижную нагрузку Линии влияния
127. Расчёт фермы на подвижную нагрузку Линии влияния
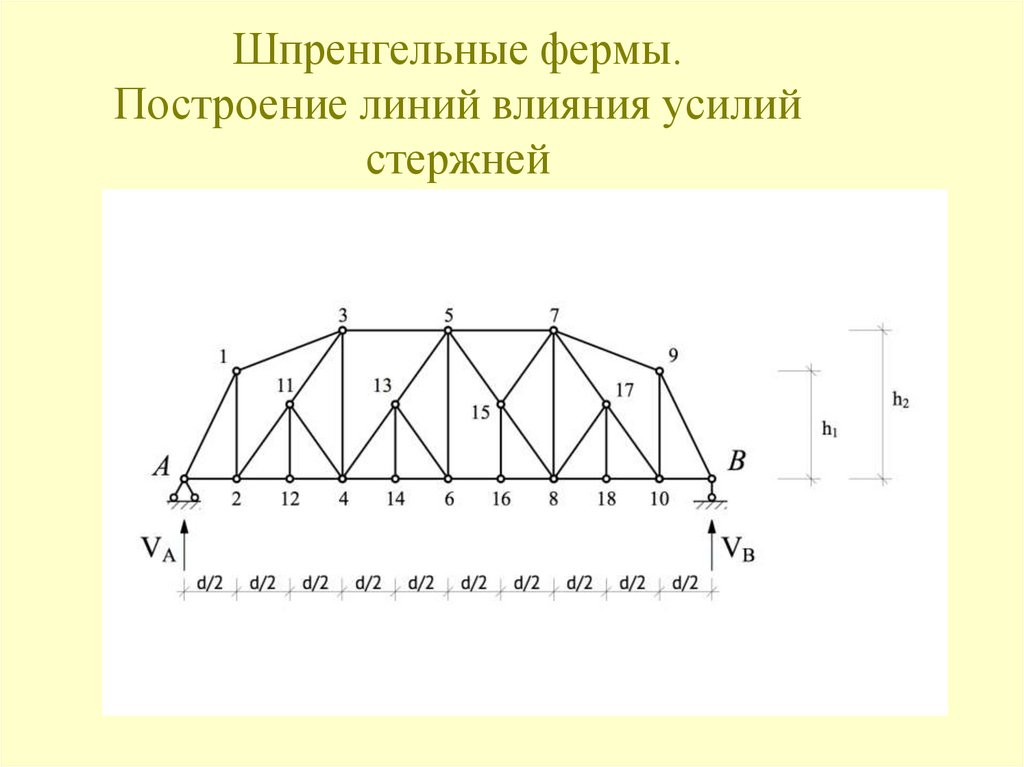
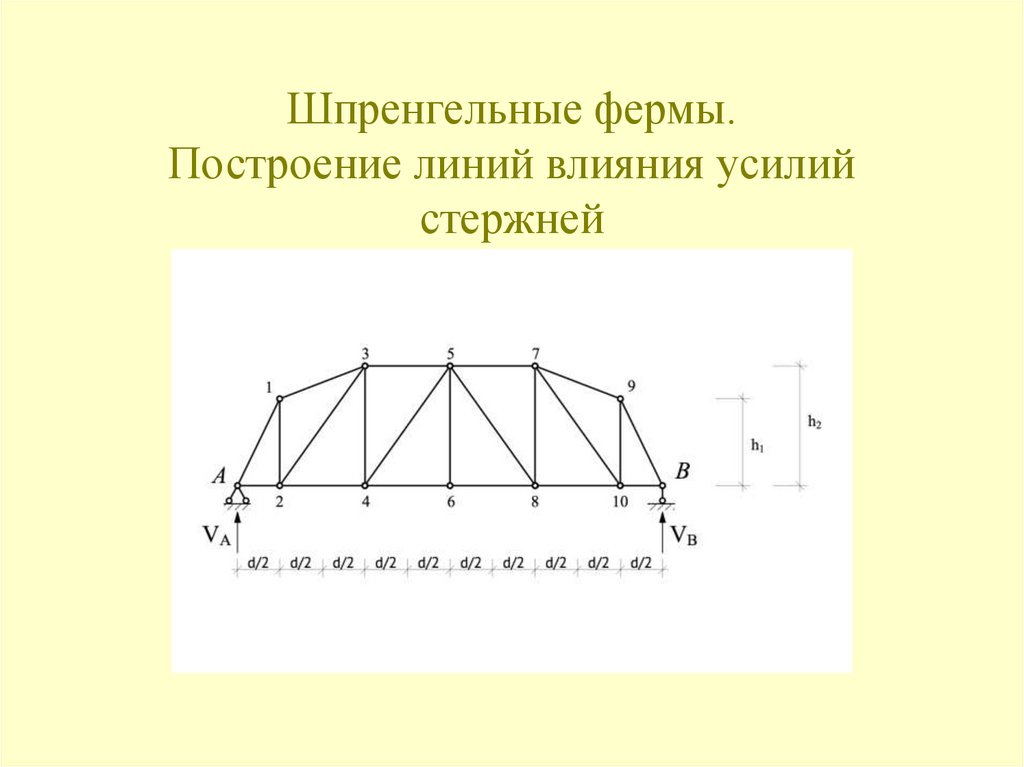
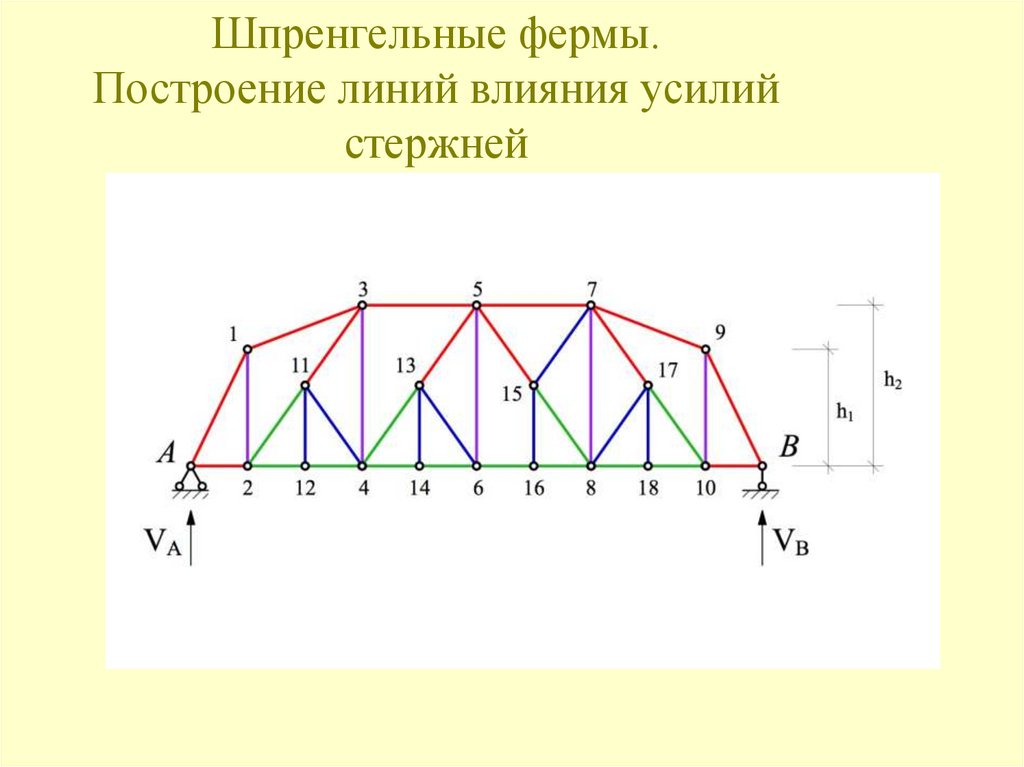
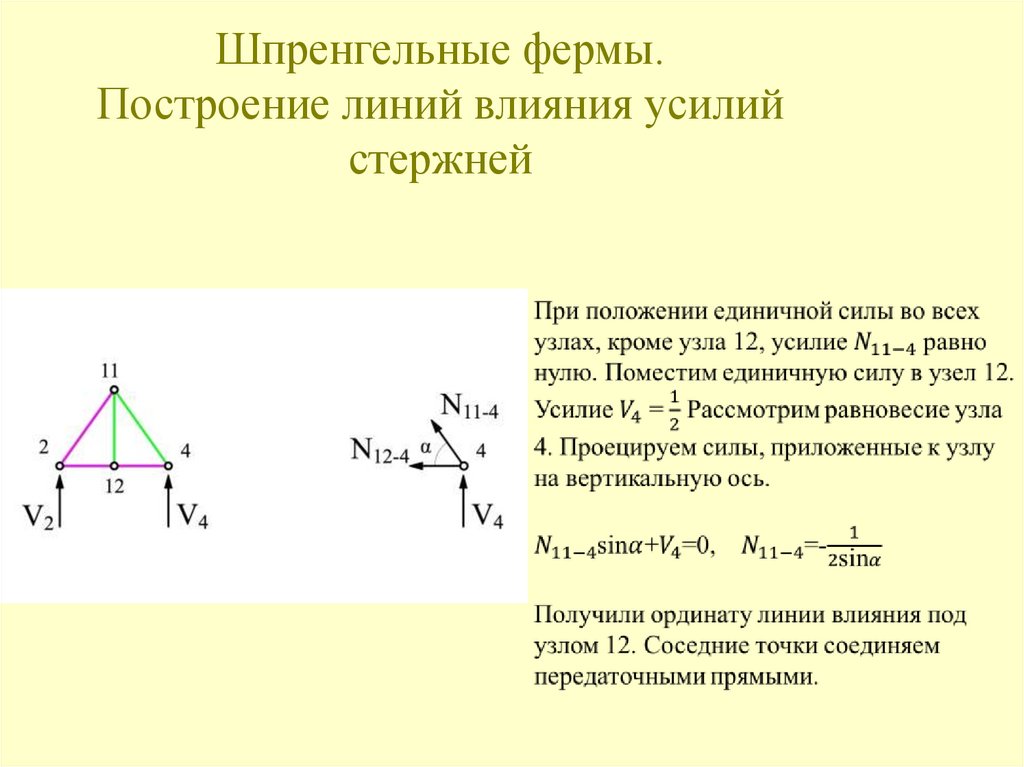
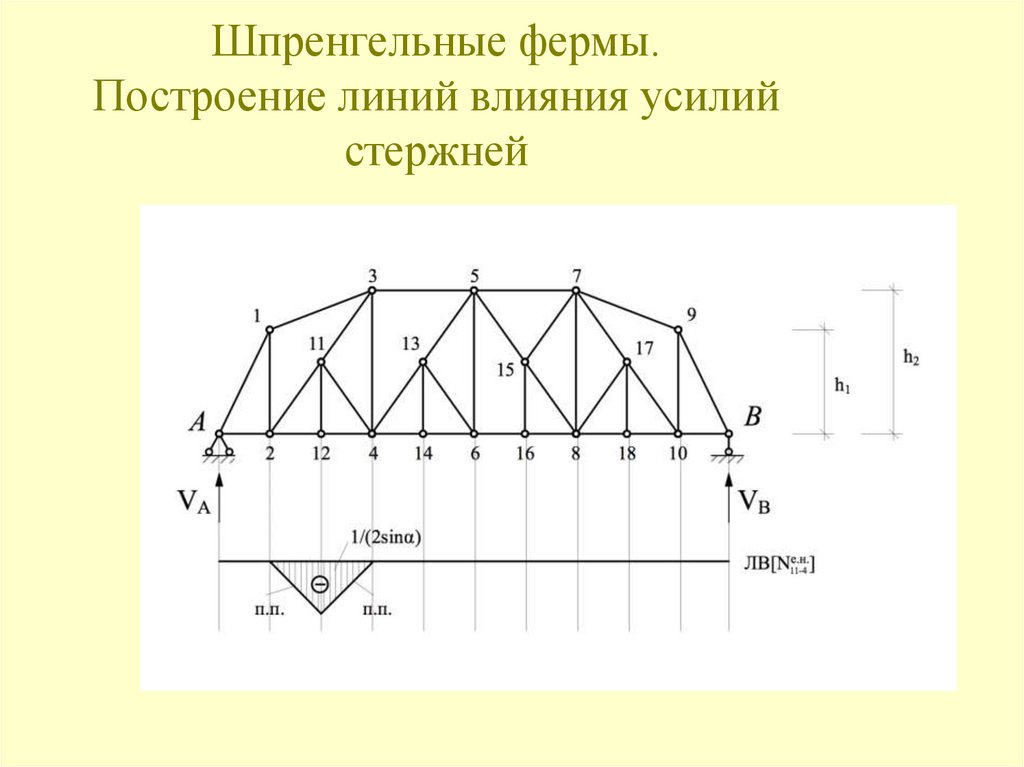
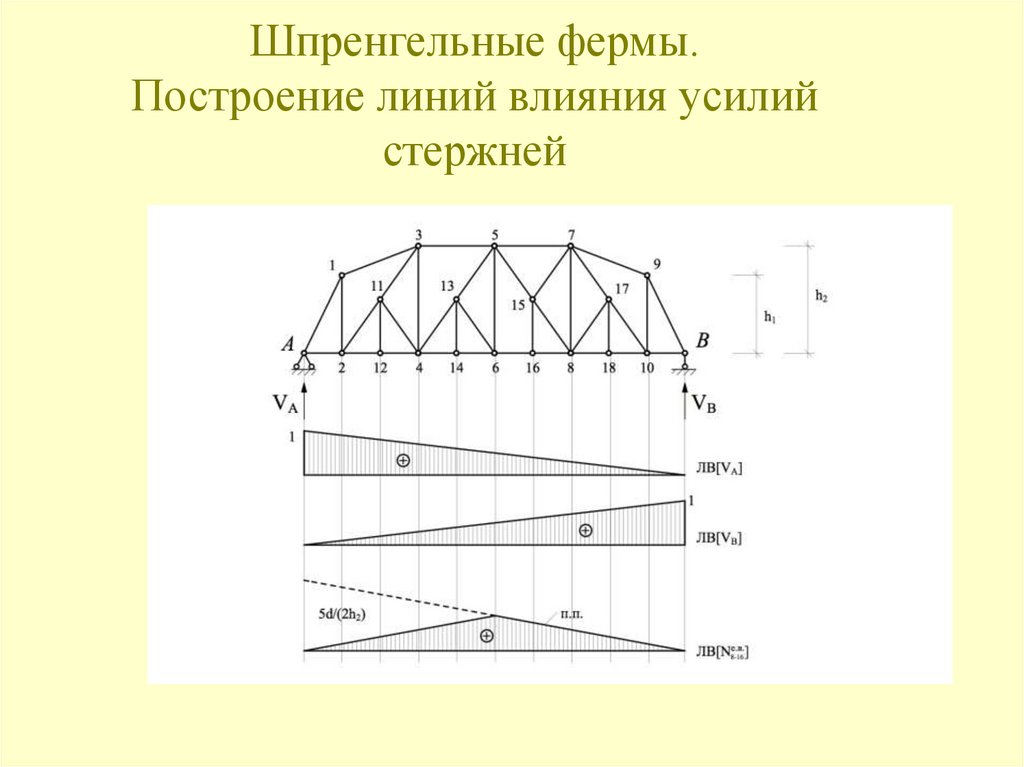
Аналогичным образом строится линия влияния усилия N2-3.128. Шпренгельные фермы. Построение линий влияния усилий стержней
1.Стержни 1-й категории.Стержни, принадлежащие основной ферме. Усилия могут быть вычислены
из условия нагружения основных узлов.
2.Стержни 2-й категории.
Стержни, принадлежащие только шпренгелю. Усилия могут быть
вычислены из расчёта шпренгеля на действие местной нагрузки.
3.Стержни 3-й категории.
Стержни, принадлежащие и основной ферме и шпренгелю. Усилия
вычисляются путём алгебраического суммирования усилий в
соответствующих стержнях основной фермы и шпренгеля.
4.Стержни 4-й категории.
Стержни, принадлежащие основной ферме, но езда «поверху» и «понизу»
различны
129. Шпренгельные фермы. Построение линий влияния усилий стержней
130. Шпренгельные фермы. Построение линий влияния усилий стержней
131. Шпренгельные фермы. Построение линий влияния усилий стержней
132. Шпренгельные фермы. Построение линий влияния усилий стержней
133. Шпренгельные фермы. Построение линий влияния усилий стержней
134. Шпренгельные фермы. Построение линий влияния усилий стержней
135. Шпренгельные фермы. Построение линий влияния усилий стержней
136. Шпренгельные фермы. Построение линий влияния усилий стержней
137.
138.
Расчет статически неопределимых рамметодом сил
1. Основы метода сил
и основные допущения для расчета рам
В статически неопределимых системах количество неизвестных
усилий (внутренних или реакций связей) n превышает количество
уравнений равновесия m для данной системы.
Метод сил состоит в отбрасывании Л = n – m «лишних» связей из
системы и заменой их на неизвестные усилия X i , которые затем
определяются из канонических уравнений метода сил.
Канонические уравнения метода сил выражают равенство нулю
действительных перемещений в отброшенных «лишних» связях, так
как в исходной системе эти связи присутствуют.
13
8
139.
Расчет статически неопределимых рамметодом сил
Перемещения точек системы определяются по формуле Мора,
которая в общем случае для плоской рамы имеет вид
M 1M p
ds
EI
Q1Qp
GAs
ds
N1 N p
EA
ds,
Где M, Q, N – соответственно изгибающие моменты, поперечные
силы и продольные силы.
В рамах с достаточно гибкими элементами перемещения узлов
системы происходят преимущественно из-за деформаций изгиба, а
деформации сдвига и сжатия-растяжения малы, поэтому в формуле
Мора будем использовать только первое слагаемое, включающее
изгибающие моменты:
M 1M p
EI
ds.
13
9
140.
Расчет статически неопределимых рамметодом сил
14
0
2. Последовательность действий при расчете
1. Определение количества лишних связей Л (степени статической
неопределимости рамы);
2. Построение статически определимой основной системы, с
отбрасыванием Л лишних связей и введением на их месте
соответствующих усилий X i . Основная система должна быть
геометрически неизменяемой;
составление системы канонических уравнений метода сил;
3. Построение в основной системе эпюр моментов M i от действия
всех единичных усилий X i 1 в отброшенных связях (по отдельности),
а также грузовой эпюры M p от действия внешней заданной нагрузки;
141.
Расчет статически неопределимых рамметодом сил
4. Определение коэффициентов канонических уравнений
(перемещений ij , ip ) путем вычисления интегралов Мора
(перемножения эпюр);
5. Решение системы канонических уравнений и определение
неизвестных усилий X i ;
6. Построение окончательной эпюры изгибающих моментов от
действия найденных усилий и итоговой эпюры моментов по формуле
n
M M p Mi Xi;
1
14
1
142.
Расчет статически неопределимых рамметодом сил
7. Выполнение кинематической (деформационной) проверки
правильности построения окончательной эпюры моментов по формуле
MM S
EI ds M M 0,
S
Где M S M1 M 2 ... M n - суммарная единичная эпюра,
т.е. результат перемножения окончательной эпюры на суммарную
единичную эпюру должен быть равен нулю.
8. Построение окончательной эпюры поперечных сил Q по эпюре
dM
;
моментов с использованием соотношения Q
dx
9. Построение эпюры продольных сил N по эпюре поперечных сил
путем вырезания узлов рамы и составления уравнений равновесия;
14
2
143.
Расчет статически неопределимых рамметодом сил
14
3
2. Пример расчета статически неопределимой рамы
методом сил
Исходная рама
Единицы измерения длины – м, сил –
кН, моментов – кНм.
Изгибная жесткость всех стержней
рамы равна EI.
Задача.
Для заданной рамы выполнить расчет на заданную нагрузку методом
сил, построить эпюры изгибающего момента M, поперечной силы Q,
продольной силы N.
144.
Расчет статически неопределимых рамметодом сил
Определение степени
статической неопределимости
Опорные реакции: VA , H A , M A ,VB , H B .
Число неизвестных n = 5.
Число уравнений равновесия m = 3.
Число лишних связей Л = 5 – 3 = 2.
Построение основной системы
Метода сил
За неизвестные приняты
опорные реакции VB и H B .
14
4
145.
Расчет статически неопределимых рамметодом сил
Система канонических уравнений метода сил для
рассматриваемой рамы имеет вид
11 X 1 12 X 2 1 p 0;
21 X 1 22 X 2 2 p 0.
ik - перемещение по направлению i-й неизвестной, вызванное
единичным усилием, приложенным по направлению k-й неизвестной.
ip - перемещение по направлению i-й неизвестной, вызванное
действием заданной внешней нагрузки.
14
5
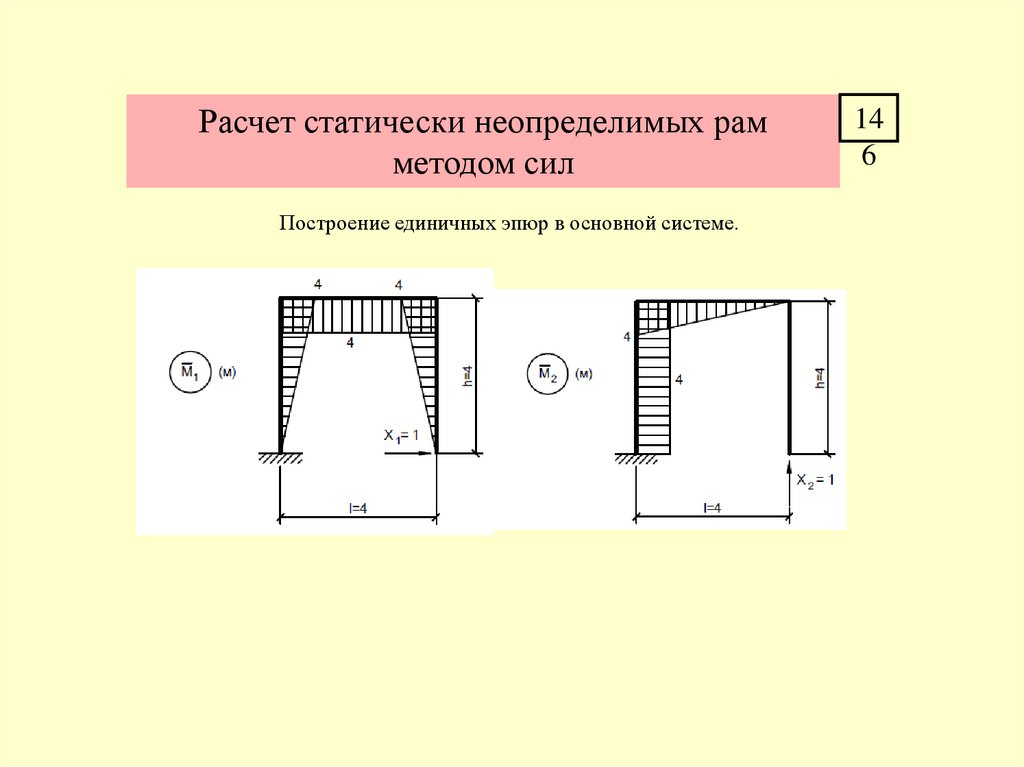
146.
Расчет статически неопределимых рамметодом сил
Построение единичных эпюр в основной системе.
14
6
147.
Расчет статически неопределимых рамметодом сил
Построение грузовой эпюры в
основной системе.
Построение суммарной единичной
эпюры M1 M 2
в основной системе.
14
7
148.
СПравило
Верещагина
(напоминание)
3
К
К
В
Чтобы вычислить интеграл от произведения двух эпюр
1
3
(«перемножить»
две эпюры), из которых хотя бы одна является
линейной, нужно
вычислить площадь Ω криволинейной эпюры и
l
l
M PMi
1 под
умножить ее наMординату
y
в
линейной
эпюре,
вычислен-ную
c
dx
yC
P M i dx yC Т
Т
А
А
EJ
EJ
М
центром тяжести
криволинейной.
02
0
М1
В
Таким образом,
и, следовательно,
3. Определим перемещения от единичных
инерционных
Примечание:
если обесил.
эпюры l линейные,
то не имеет значения, в
MM
ij i j dx
– формула Мора
EI Ω, а у какой – ординату yc.
какой из эпюр вычислять площадь
0
ил
и
l
M 12
11
dx;
EI
0
l
M 22
22
dx;
EI
0
l
M 1M 2
dx.
EI
0
12 21
Для «перемножения эпюр» воспользуемся правилом Верещагина
149.
1,5 EJ Верещагина1,5 EJ С
Правило
(напоминание)
3
К
К
В
Чтобы вычислить интеграл от произведения двух эпюр
1
3
(«перемножить»
две эпюры), из которых хотя бы одна является
линейной, EJ
нужно
вычислить площадь Ω криволинейной эпюры и
l
l
M PMi
1 под
умножить ее наMординату
y
в
линейной
эпюре,
вычислен-ную
c
dx
yC
P M i dx yC Т
Т
А
А
EJ
EJ
М
центром тяжести
криволинейной.
02
0
М1
В
Таким образом,
и, следовательно,
3. Определим перемещения от единичных
инерционных
сил. линейные, то не имеет значения в
Примечание:
если обе эпюры
M
из
dx вычислять площадь Ω, а у какой – ординату y .
эпюр
какой
c
EI
l
11
0
2
1
150.
Расчет статически неопределимых рамметодом сил
Вычисление коэффициентов канонических уравнений.
Перемножение эпюр при вычислении произведем,
пользуясь правилом Верещагина.
11
M 1M 1
4 4 4 4 4 4 106,67
ds 2
.
EI
3EI
EI
EI
22
M 2M 2
4 4 4 4 4 4 85,33
ds
.
EI
EI
3EI
EI
12 21
M 1M 2
4 4 4 4 4 4 64
ds
.
EI
2 EI
2 EI
EI
1P
M 1M P
2 10 2
6,67
ds
.
EI
6 EI
EI
2 P
M 2M P
2 10 4
40
ds
.
EI
2 EI
EI
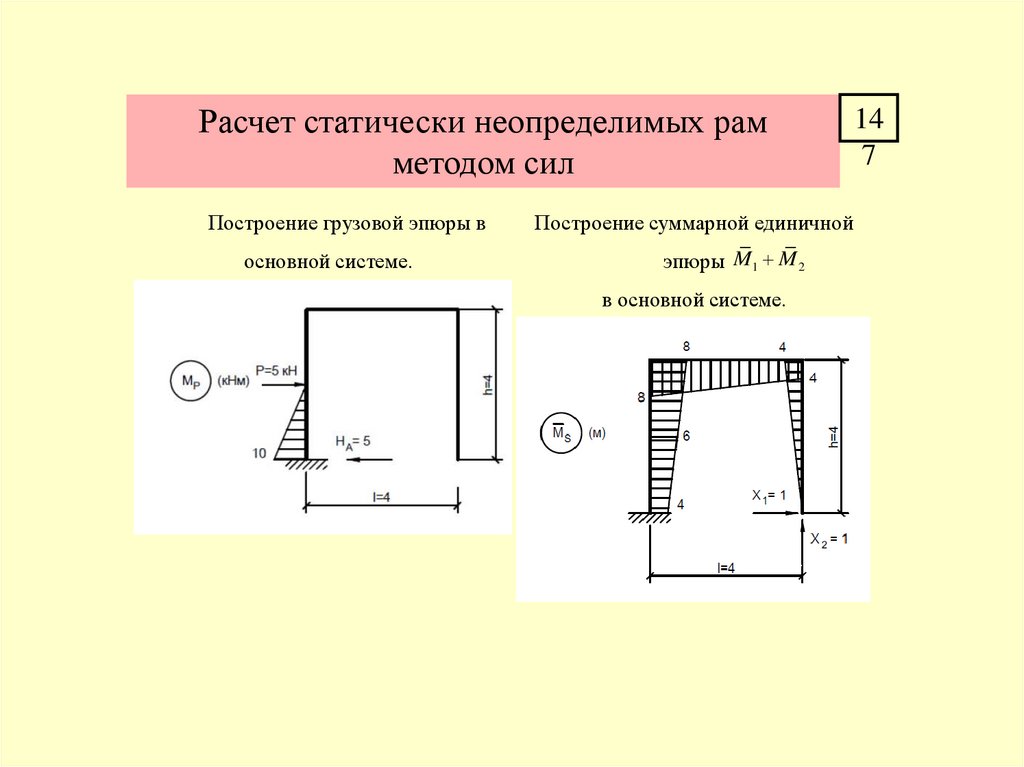
15
0
151.
Расчет статически неопределимых рамметодом сил
15
1
Подставим найденные значения коэффициентов в систему канонических
уравнений и умножим все полученные уравнения на EI.
Получим:
106,67 X1 64 X 2 6,67 0;
64 X1 85,33 X 2 40 0.
Решая эту систему, получим значения неизвестных метода сил:
X 1 0,4 кН,
X 2 0,77 кН.
152.
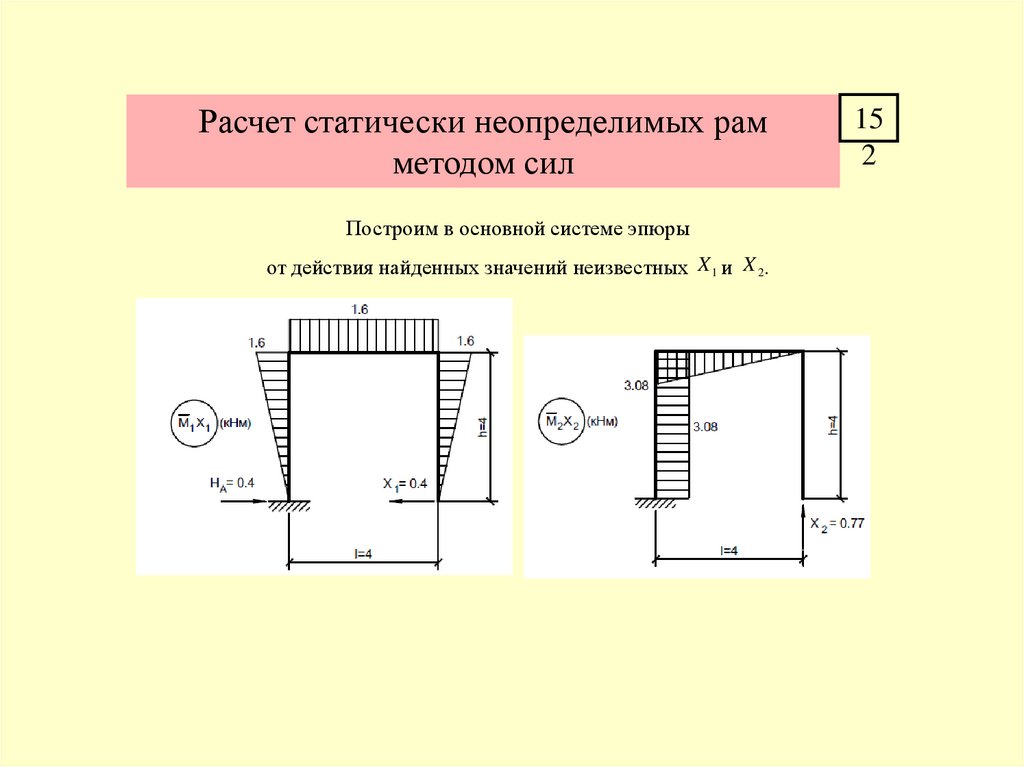
Расчет статически неопределимых рамметодом сил
Построим в основной системе эпюры
от действия найденных значений неизвестных X 1 и X 2.
15
2
153.
Расчет статически неопределимых рамметодом сил
15
3
Построим в исходной системе окончательную эпюру моментов
По формуле M M p M 1 X 1 M 2 X 2 .
Выполним кинематическую проверку.
2
2
M MS
( 2 4 6,92 2 6 2,28 6 6,92 4 2,28)
(2 6 2,28 2 8 1,48
6 EI
6 EI
4
4 4 1,6 0,053
6 1,48 8 2,28)
(2 8 1,48 2 4 1,6 4 1,48 8 1,6)
.
6 EI
3EI
EI
154.
Расчет статически неопределимых рамметодом сил
Построим в исходной системе окончательную эпюру поперечных сил,
dM
используя соотношение Q
.
dx
Для участков, где эпюра момента линейна, это соотношение можно
M MA
Q B
,
записать в виде
где в числителе – моменты в начале и
l
конце участка (с учетом правила знаков), а в знаменателе – длина участка
эпюры.
15
4
155.
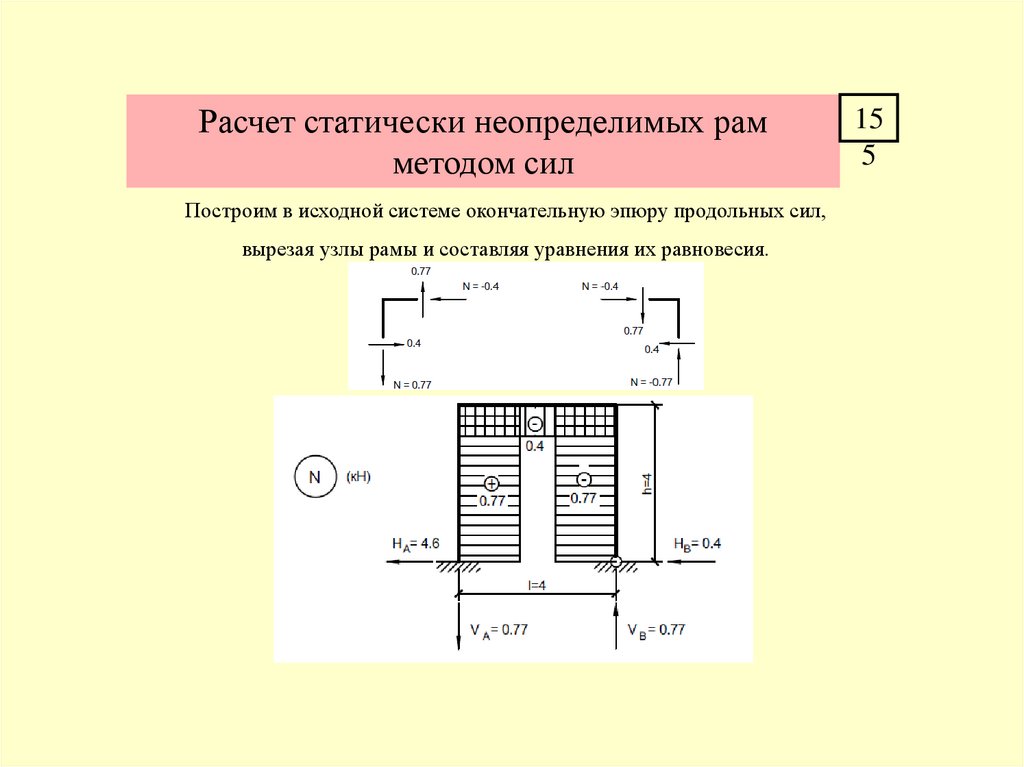
Расчет статически неопределимых рамметодом сил
Построим в исходной системе окончательную эпюру продольных сил,
вырезая узлы рамы и составляя уравнения их равновесия.
15
5










































































 physics
physics